Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry
Подождите немного. Документ загружается.


Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
cos a=b,90<<180
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0
x 2y, y, z 4 1 2
a b,90<<180
Cccm nn2=m
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0 y
1
4
, x
1
4
, z
1
4
4 1 2
a b, 90
P4
2
=mmc
2=m2=mn
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z; y
1
4
, x
1
4
, z
1
4
4 1 4
16 P222 a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 8 2 1
a b 6 cP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 y, x, z 8 2 2
a b cPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 z, x, y; y, x, z 8 2 6
17 P222
1
a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 8 2 1
a bP4
2
=mmc
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 y, x, z
1
4
8 2 2
18 P2
1
2
1
2 a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 8 2 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 y, x, z 8 2 2
19 P2
1
2
1
2
1
a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 8 2 1
a b 6 cP4
2
=mmc
2=m2=mn
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 y
1
4
, x
1
4
, z
1
4
8 2 2
a b cPm
3n
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
0, 0, 0 z, x, y; y
1
4
, x
1
4
, z
1
4
8 2 6
20 C222
1
a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
0, 0, 0 4 2 1
a bP4
2
=mmc
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
0, 0, 0 y, x, z
1
4
4 2 2
21 C222 a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
0, 0, 0 4 2 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
0, 0, 0 y, x, z 4 2 2
22 F222 a 6 b 6 c 6 a Immm
1
2
a,
1
2
b,
1
2
c
1
4
,
1
4
,
1
4
0, 0, 0 4 2 1
a b 6 cI4=mmm
1
2
a,
1
2
b,
1
2
c
1
4
,
1
4
,
1
4
0, 0, 0 y, x, z 4 2 2
a b cIm
3m
1
2
a,
1
2
b,
1
2
c
1
4
,
1
4
,
1
4
0, 0, 0 z, x, y; y, x, z 4 2 6
23 I222 a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
, 0 0, 0, 0 4 2 1
a b 6 cP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
, 0 0, 0, 0 y, x, z 4 2 2
a b cPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
, 0 0, 0, 0 z,x, y; y, x, z 4 2 6
24 I2
1
2
1
2
1
a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
, 0 0, 0, 0 4 2 1
a b 6 cP4
2
=mmc
2=m2=mn
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
, 0 0, 0, 0 y
1
4
, x
1
4
, z
1
4
4 2 2
a b cPm
3n
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
, 0 0, 0, 0 z, x, y; y
1
4
, x
1
4
, z
1
4
4 2 6
25 Pmm2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z 4 12 2
26 Pmc2
1
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
27 Pcc2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z 4 12 2
28 Pma2 P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
29 Pca2
1
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
30 Pnc2 P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
31 Pmn2
1
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
891
15.2. EUCLIDEAN AND AFFINE NORMALIZERS

Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
32 Pba2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z 4 12 2
33 Pna2
1
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
34 Pnn2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z 4 12 2
35 Cmm2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 y, x, z 2 12 2
36 Cmc2
1
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
37 Ccc2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 y, x, z 2 12 2
38 Amm2 P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
39 Aem2 P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
40 Ama2 P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
41 Aea2 P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
42 Fmm2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c 0, 0, t 0, 0, 0 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c 0, 0, t 0, 0, 0 y, x, z 12 2
43 Fdd2 a 6 bP
1
ban 222
1
2
a,
1
2
b, "c 0, 0, t
1
8
,
1
8
,0 12 1
a bP
1
4=nbm
42m
1
2
a,
1
2
b, "c 0, 0, t
1
8
,
1
8
,0 y , x, z 12 2
44 Imm2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 y, x, z 2 12 2
45 Iba2 a 6 bP
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
a bP
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 y, x, z 2 12 2
46 Ima2 P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,0,t 0, 0, 0 2 12 1
47 Pmmm a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a b 6 cP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
a b cPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, x, y; y, x, z 8 1 6
48 Pnnn (both
origins)
a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a b 6 cP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
a b cPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, x, y; y, x, z 8 1 6
49 Pccm a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
50 Pban (both
origins)
a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
51 Pmma Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
52 Pnna Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
53 Pmna Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
54 Pcca Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
892
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY

Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
55 Pbam a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
56 Pccn a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
57 Pbcm Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
58 Pnnm a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
59 Pmmn (both
origins)
a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
60 Pbcn Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
61 Pbca a 6 b or b 6 c or a 6 c Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a b cPm
3
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, x, y 8 1 3
62 Pnma Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
63 Cmcm Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
64 Cmce Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
65 Cmmm a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
y, x, z 4 1 2
66 Cccm a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
y, x, z 4 1 2
67 Cmme a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
a bP4=mmm (mmm)
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
y
1
4
, x
1
4
, z 4 1 2
68 Ccce 222 a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
y, x, z 4 1 2
68 Ccce
1 a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
a bP4=mmm (mmm)
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
y
1
4
, x
1
4
, z 4 1 2
69 Fmmm a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 2 1 1
a b 6 cP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 y, x, z 2 1 2
a b cPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 z, x, y; y, x, z 2 1 6
70 Fddd 222 a 6 b 6 c 6 a Pnnn 222
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 2 1 1
a b 6 cP4
2
=nnm
42m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 y, x, z 2 1 2
a b cPn
3m
43m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 z, x, y; y, x, z 2 1 6
70 Fddd
1 a 6 b 6 c 6 a Pnnn
1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 2 1 1
a b 6 cP4
2
=nnm
2=m at 0,
1
2
,0
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 y, x, z 2 1 2
a b cPn
3m
3m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0 z, x, y; y, x, z 2 1 6
71 Immm a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a b 6 cP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 y, x, z 4 1 2
a b cPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 z, x, y; y, x, z 4 1 6
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
893
15.2. EUCLIDEAN AND AFFINE NORMALIZERS
combinations of matrices and vectors that originate from the
specified pair(s) and from the restrictions on the coefficients. This
set of matrix–vector pairs has of course to include the symmetry
operations of G as well as of N
E
G.
The relatively complicated group structure of these affine
normalizers has to do with the fact that for the corresponding
space groups the permissible basis transformations are more
complicated than for space groups of higher crystal systems.
In contrast to orthorhombic space groups, the metric of a triclinic
or monoclinic space group cannot be specialized in such a way that
all elements of the affine normalizer simultaneously become
isometries.
The affine normalizers of the oblique plane groups p1 and p2 can
be described analogously. The corresponding unimodular matrix
n
11
n
12
n
21
n
22
has to be combined with the vector
r
s
or
1
2
n
1
1
2
n
2
for the representation of N
A
p1 and N
A
p2, respectively. n stands
for an integer number, r and s stand for real numbers.
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
72 Ibam a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a bP4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 y, x, z 4 1 2
73 Ibca a 6 b 6 c 6 a Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a b 6 cP4
2
=mmc
2=m2=mn
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 y
1
4
, x
1
4
, z
1
4
4 1 2
a b cPm
3n
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 z, x, y;41 6
y
1
4
, x
1
4
, z
1
4
74 Imma a 6 b Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a bP4
2
=mmc
2=m2=mn
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 y
1
4
, x
1
4
, z
1
4
4 1 2
894
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY
Table 15.2.1.4. Euclidean normalizers of the tetragonal, trigonal, hexagonal and cubic space groups
The symbols in parentheses following a space-group symbol refer to the location of the origin (‘origin choice’ in Part 7).
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of G in
N
E
G
No.
Hermann–
Mauguin symbol Symbol Basis vectors Translations
Inversion
through a
centre at
Further
generators
75 P4 P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 y, x, z 2 12 2
76 P4
1
P
1
422
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t / y, x, z 2 12
77 P4
2
P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 y, x, z 2 12 2
78 P4
3
P
1
422
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t / y, x, z 2 12
79 I4 P
1
4=mmm
1
2
a b,
1
2
a b, "c 0, 0, t 0, 0, 0 y, x, z 12 2
80 I4
1
P
1
4=nbm
42m
1
2
a b,
1
2
a b, "c 0, 0, t
1
4
,0,0 y, x, z 12 2
81 P
4 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 y, x, z 4 2 2
82 I
4 I4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,
1
4
0, 0, 0 y, x, z 4 2 2
83 P4=mP4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
y, x, z 4 1 2
84 P4
2
=mP4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
y, x, z 4 1 2
85 P4=n
4 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
y, x, z 4 1 2
85 P4=n
1 P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
y, x, z 4 1 2
86 P4
2
=n
4 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
y, x, z 4 1 2
86 P4
2
=n
1 P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
y, x, z 4 1 2
87 I4=mP4=mmm
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
y, x, z 2 1 2
88 I4
1
=a
4 P4
2
=nnm
42m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
y, x, z 2 1 2
88 I4
1
=a
1 P4
2
=nnm 2=m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
y
1
4
, x
1
4
, z
1
4
2 1 2
89 P422 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
90 P42
1
2 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
91 P4
1
22 P4
2
22 222
origin at 4
2
12
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
/4 1
92 P4
1
2
1
2 P4
2
22
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
/4 1
93 P4
2
22 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
94 P4
2
2
1
2 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
95 P4
3
22 P4
2
22 222
origin at 4
2
12
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
/4 1
96 P4
3
2
1
2 P4
2
22
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
/4 1
97 I422 P4=mmm
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
0, 0, 0 2 2 1
98 I4
1
22 P4
2
=nnm
42m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
1
4
,0,
1
8
2 2 1
99 P4mm P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
100 P4bm P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
101 P4
2
cm P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
102 P4
2
nm P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
103 P4cc P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
104 P4nc P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
105 P4
2
mc P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
106 P4
2
bc P
1
4=mmm
1
2
a b,
1
2
a b, "c
1
2
,
1
2
,0;0,0,t 0, 0, 0 2 12 1
107 I4mm P
1
4=mmm
1
2
a b,
1
2
a b, "c 0, 0, t 0, 0, 0 12 1
108 I4cm P
1
4=mmm
1
2
a b,
1
2
a b, "c 0, 0, t 0, 0, 0 12 1
109 I4
1
md P
1
4=nbm
42m
1
2
a b,
1
2
a b, "c 0, 0, t
1
4
,0,0 12 1
110 I4
1
cd P
1
4=nbm
42m
1
2
a b,
1
2
a b, "c 0, 0, t
1
4
,0,0 12 1
111 P
42mP4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
112 P
42cP4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
113 P
42
1
mP4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
114 P
42
1
cP4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
115 P
4m2 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
116 P
4c2 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
117 P
4b2 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
118 P
4n2 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
0, 0, 0 4 2 1
119 I
4m2 I4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,
1
4
0, 0, 0 4 2 1
895
15.2. EUCLIDEAN AND AFFINE NORMALIZERS
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of G in
N
E
G
No.
Hermann–
Mauguin symbol Symbol Basis vectors Translations
Inversion
through a
centre at
Further
generators
120 I
4c2 I4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,
1
4
0, 0, 0 4 2 1
121 I
42mP4=mmm
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
0, 0, 0 2 2 1
122 I
42dP4
2
=nnm
42m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
1
4
,0,
1
8
2 2 1
123 P4= mmm P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
124 P4= mcc P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
125 P4= nbm 422 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
125 P4= nbm 2=m P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
126 P4= nnc 422 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
126 P4= nnc
1 P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
127 P4= mbm P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
128 P4= mnc P4= mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
129 P4= nmm
4m2 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
129 P4= nmm 2=m P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
130 P4= ncc
4 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
130 P4= ncc
1 P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
131 P4
2
=mmc P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
132 P4
2
=mcm P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
133 P4
2
=nbc
4 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
133 P4
2
=nbc
1 P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
134 P4
2
=nnm
42m P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
134 P4
2
=nnm 2=m P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
135 P4
2
=mbc P4 =mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
136 P4
2
=mnm P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
137 P4
2
=nmc
4m2 P4 =mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
137 P4
2
=nmc
1 P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
138 P4
2
=ncm
4 P4=mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
138 P4
2
=ncm 2=m P4=mmm mmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,
1
2
,0;0,0,
1
2
4 1 1
139 I4=mmm P4=mmm
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
2 1 1
140 I4=mcm P4=mmm
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
2 1 1
141 I4
1
=amd
4m2 P4
2
=nnm
42m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
2 1 1
141 I4
1
=amd 2=m P4
2
=nnm 2=m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
2 1 1
142 I4
1
=acd
4 P4
2
=nnm
42m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
2 1 1
142 I4
1
=acd
1 P4
2
=nnm 2=m
1
2
a b,
1
2
a b,
1
2
c 0, 0,
1
2
2 1 1
143 P3 P
1
6=mmm
2
3
a
1
3
b,
1
3
a
1
3
b, "c
2
3
,
1
3
,0;0,0,t 0, 0, 0 x, y, z; y, x, z 3 12 4
144 P3
1
P
1
622
2
3
a
1
3
b,
1
3
a
1
3
b, "c
2
3
,
1
3
,0;0,0,t / x , y, z; y, x, z 3 14
145 P3
2
P
1
622
2
3
a
1
3
b,
1
3
a
1
3
b, "c
2
3
,
1
3
,0;0,0,t / x , y, z; y, x, z 3 14
146 R3 (hexag.) P
1
31m
2
3
a
1
3
b,
1
3
a
1
3
b, "c 0, 0, t 0, 0, 0 y, x, z 12 2
146 R3 (rhomboh.) P
1
31m
2
3
a
1
3
b
1
3
c,
1
3
a
2
3
b
1
3
c, "a b c
r, r, r 0, 0, 0 y, x, z 12 2
147 P
3 P6=mmm a, b,
1
2
c 0, 0,
1
2
x, y, z; y, x, z 2 1 4
148 R
3 (hexag.) R
3m (hexag.) a, b,
1
2
c 0, 0,
1
2
y, x, z 2 1 2
148 R
3 (rhomboh.) R
3m (rhomboh.)
1
2
a b c,
1
2
a b c,
1
2
a b c
1
2
,
1
2
,
1
2
y, x, z 2 1 2
149 P312 P6=mmm
2
3
a
1
3
b,
1
3
a
1
3
b,
1
2
c
2
3
,
1
3
,0;0,0,
1
2
0, 0, 0 x, y, z 6 2 2
150 P321 P6=mmm a, b,
1
2
c 0, 0,
1
2
0, 0, 0 x, y, z 2 2 2
151 P3
1
12 P6
2
22
2
3
a
1
3
b,
1
3
a
1
3
b,
1
2
c
2
3
,
1
3
,0;0,0,
1
2
/ x, y, z 6 2
152 P3
1
21 P6
2
22 a b, a,
1
2
c 0, 0,
1
2
/ x, y, z 2 2
153 P3
2
12 P6
4
22
2
3
a
1
3
b,
1
3
a
1
3
b,
1
2
c
2
3
,
1
3
,0;0,0,
1
2
/ x, y, z 6 2
154 P3
2
21 P6
4
22 a b, a,
1
2
c 0, 0,
1
2
/ x, y, z 2 2
155 R32 (hexag.) R
3m (hexag.) a, b,
1
2
c 0, 0,
1
2
0, 0, 0 2 2 1
155 R32 (rhomboh.) R
3m (rhomboh.)
1
2
a b c,
1
2
a b c,
1
2
a b c
1
2
,
1
2
,
1
2
0, 0, 0 2 2 1
Table 15.2.1.4. Euclidean normalizers of the tetragonal, trigonal, hexagonal and cubic space groups ( cont.)
896
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY

Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of G in
N
E
G
No.
Hermann–
Mauguin symbol Symbol Basis vectors Translations
Inversion
through a
centre at
Further
generators
156 P3m1 P
1
6=mmm
2
3
a
1
3
b,
1
3
a
1
3
b, "c
2
3
,
1
3
,0;0,0,t 0, 0, 0 x, y, z 3 12 2
157 P31mP
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 x, y, z 12 2
158 P3c1 P
1
6=mmm
2
3
a
1
3
b,
1
3
a
1
3
b, "c
2
3
,
1
3
,0;0,0,t 0, 0, 0 x, y, z 3 12 2
159 P31cP
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 x, y, z 12 2
160 R3m (hexag.) P
1
31m
2
3
a
1
3
b,
1
3
a
1
3
b, "c 0, 0, t 0, 0, 0 12 1
160 R3m (rhomboh.) P
1
31m
2
3
a
1
3
b
1
3
c,
1
3
a
2
3
b
1
3
c, "a b c
r, r, r 0, 0, 0 12 1
161 R3c (hexag.) P
1
31m
2
3
a
1
3
b,
1
3
a
1
3
b, "c 0, 0, t 0, 0, 0 12 1
161 R3c (rhomboh.) P
1
31m
2
3
a
1
3
b
1
3
c,
1
3
a
2
3
b
1
3
c, "a b c
r, r, r 0, 0, 0 12 1
162 P
31mP6=mmm a, b,
1
2
c 0, 0,
1
2
x, y, z 2 1 2
163 P
31cP6=mmm a, b,
1
2
c 0, 0,
1
2
x, y, z 2 1 2
164 P
3m1 P6=mmm a, b,
1
2
c 0, 0,
1
2
x, y, z 2 1 2
165 P
3c1 P6=mmm a, b,
1
2
c 0, 0,
1
2
x, y, z 2 1 2
166 R
3m (hexag.) R
3m (hexag.) a, b,
1
2
c 0, 0,
1
2
2 1 1
166 R
3m (rhomboh.) R
3m (rhomboh.)
1
2
a b c,
1
2
a b c,
1
2
a b c
1
2
,
1
2
,
1
2
2 1 1
167 R
3c (hexag.) R
3m (hexag.) a, b,
1
2
c 0, 0,
1
2
2 1 1
167 R
3c (rhomboh.) R
3m (rhomboh.)
1
2
a b c,
1
2
a b c,
1
2
a b c
1
2
,
1
2
,
1
2
2 1 1
168 P6 P
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 y, x, z 12 2
169 P6
1
P
1
622 a, b, "c 0, 0, t / y, x, z 12
170 P6
5
P
1
622 a, b, "c 0, 0, t / y, x, z 12
171 P6
2
P
1
622 a, b, "c 0, 0, t / y, x, z 12
172 P6
4
P
1
622 a, b, "c 0, 0, t / y, x, z 12
173 P6
3
P
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 y, x, z 12 2
174 P
6 P6=mmm
2
3
a
1
3
b,
1
3
a
1
3
b,
1
2
c
2
3
,
1
3
,0;0,0,
1
2
0, 0, 0 y, x, z 6 2 2
175 P6= mP6=mmm a, b,
1
2
c 0, 0,
1
2
y, x, z 2 1 2
176 P6
3
=mP6=mmm a, b,
1
2
c 0, 0,
1
2
y, x, z 2 1 2
177 P622 P6=mmm a, b,
1
2
c 0, 0,
1
2
0, 0, 0 2 2 1
178 P6
1
22 P6
2
22 a, b,
1
2
c 0, 0,
1
2
/2 1
179 P6
5
22 P6
4
22 a, b,
1
2
c 0, 0,
1
2
/2 1
180 P6
2
22 P6
4
22 a, b,
1
2
c 0, 0,
1
2
/2 1
181 P6
4
22 P6
2
22 a, b,
1
2
c 0, 0,
1
2
/2 1
182 P6
3
22 P6=mmm a, b,
1
2
c 0, 0,
1
2
0, 0, 0 2 2 1
183 P6mm P
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 12 1
184 P6cc P
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 12 1
185 P6
3
cm P
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 12 1
186 P6
3
mc P
1
6=mmm a, b, "c 0, 0, t 0, 0, 0 12 1
187 P
6m2 P6=mmm
2
3
a
1
3
b,
1
3
a
1
3
b,
1
2
c
2
3
,
1
3
,0;0,0,
1
2
0, 0, 0 6 2 1
188 P
6c2 P6=mmm
2
3
a
1
3
b,
1
3
a
1
3
b,
1
2
c
2
3
,
1
3
,0;0,0,
1
2
0, 0, 0 6 2 1
189 P
62mP6=mmm a, b,
1
2
c 0, 0,
1
2
0, 0, 0 2 2 1
190 P
62cP6=mmm a, b,
1
2
c 0, 0,
1
2
0, 0, 0 2 2 1
191 P6= mmm P6=mmm a, b,
1
2
c 0, 0,
1
2
2 1 1
192 P6= mcc P6=mmm a, b,
1
2
c 0, 0,
1
2
2 1 1
193 P6
3
=mcm P6=mmm a, b,
1
2
c 0, 0,
1
2
2 1 1
194 P6
3
=mmc P6=mmm a, b,
1
2
c 0, 0,
1
2
2 1 1
195 P23 Im
3m a, b, c
1
2
,
1
2
,
1
2
0, 0, 0 y, x, z 2 2 2
196 F23 Im
3m
1
2
a,
1
2
b,
1
2
c
1
4
,
1
4
,
1
4
0, 0, 0 y, x, z 4 2 2
197 I23 Im
3m a, b, c 0, 0, 0 y, x, z 1 2 2
Table 15.2.1.4. Euclidean normalizers of the tetragonal, trigonal, hexagonal and cubic space groups ( cont.)
897
15.2. EUCLIDEAN AND AFFINE NORMALIZERS
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of G in
N
E
G
No.
Hermann–
Mauguin symbol Symbol Basis vectors Translations
Inversion
through a
centre at
Further
generators
198 P2
1
3 Ia
3d a, b, c
1
2
,
1
2
,
1
2
0, 0, 0 y
1
4
, x
1
4
, z
1
4
2 2 2
199 I2
1
3 Ia
3d a, b, c 0, 0, 0 y
1
4
, x
1
4
, z
1
4
1 2 2
200 Pm
3 Im
3m a, b, c
1
2
,
1
2
,
1
2
y, x, z 2 1 2
201 Pn
3 23 Im
3m a, b, c
1
2
,
1
2
,
1
2
y, x, z 2 1 2
201 Pn
3
3 Im
3m
3m a, b, c
1
2
,
1
2
,
1
2
y, x, z 2 1 2
202 Fm
3 Pm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
y, x, z 2 1 2
203 Fd
3 23 Pn
3m
43m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
y, x, z 2 1 2
203 Fd
3
3 Pn
3m
3m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
y, x, z 2 1 2
204 Im
3 Im
3m a, b, c y, x, z 1 1 2
205 Pa
3 Ia
3 a, b, c
1
2
,
1
2
,
1
2
2 1 1
206 Ia
3 Ia
3d a, b, c y
1
4
, x
1
4
, z
1
4
1 1 2
207 P432 Im
3m a, b, c
1
2
,
1
2
,
1
2
0, 0, 0 2 2 1
208 P4
2
32 Im
3m a, b, c
1
2
,
1
2
,
1
2
0, 0, 0 2 2 1
209 F432 Pm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
0, 0, 0 2 2 1
210 F4
1
32 Pn
3m
43m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
1
8
,
1
8
,
1
8
2 2 1
211 I432 Im
3m a, b, c 0, 0, 0 1 2 1
212 P4
3
32 I4
1
32 a, b, c
1
2
,
1
2
,
1
2
/2 1
213 P4
1
32 I4
1
32 a, b, c
1
2
,
1
2
,
1
2
/2 1
214 I4
1
32 Ia
3d a, b, c 0, 0, 0 1 2 1
215 P
43mIm
3m a, b, c
1
2
,
1
2
,
1
2
0, 0, 0 2 2 1
216 F
43mIm
3m
1
2
a,
1
2
b,
1
2
c
1
4
,
1
4
,
1
4
0, 0, 0 4 2 1
217 I
43mIm
3m a, b, c 0, 0, 0 1 2 1
218 P
43nIm
3m a, b, c
1
2
,
1
2
,
1
2
0, 0, 0 2 2 1
219 F
43cIm
3m
1
2
a,
1
2
b,
1
2
c
1
4
,
1
4
,
1
4
0, 0, 0 4 2 1
220 I
43dIa
3d a, b, c 0, 0, 0 1 2 1
221 Pm
3mIm
3m a, b, c
1
2
,
1
2
,
1
2
2 1 1
222 Pn
3n 432 Im
3m a, b, c
1
2
,
1
2
,
1
2
2 1 1
222 Pn
3n
3 Im
3m
3m a, b, c
1
2
,
1
2
,
1
2
2 1 1
223 Pm
3nIm
3m a, b, c
1
2
,
1
2
,
1
2
2 1 1
224 Pn
3m
43m Im
3m a, b, c
1
2
,
1
2
,
1
2
2 1 1
224 Pn
3m
3m Im
3m
3m a, b, c
1
2
,
1
2
,
1
2
2 1 1
225 Fm
3mPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
2 1 1
226 Fm
3cPm
3m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
2 1 1
227 Fd
3m
43m Pn
3m
43m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
2 1 1
227 Fd
3m
3m Pn
3m
3m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
2 1 1
228 Fd
3c 23 Pn
3m
43m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
2 1 1
228 Fd
3c
3 Pn
3m
3m
1
2
a,
1
2
b,
1
2
c
1
2
,
1
2
,
1
2
2 1 1
229 Im
3mIm
3m a, b, c 1 1 1
230 Ia
3dIa
3d a, b, c 1 1 1
Table 15.2.1.4. Euclidean normalizers of the tetragonal, trigonal, hexagonal and cubic space groups ( cont.)
898
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY
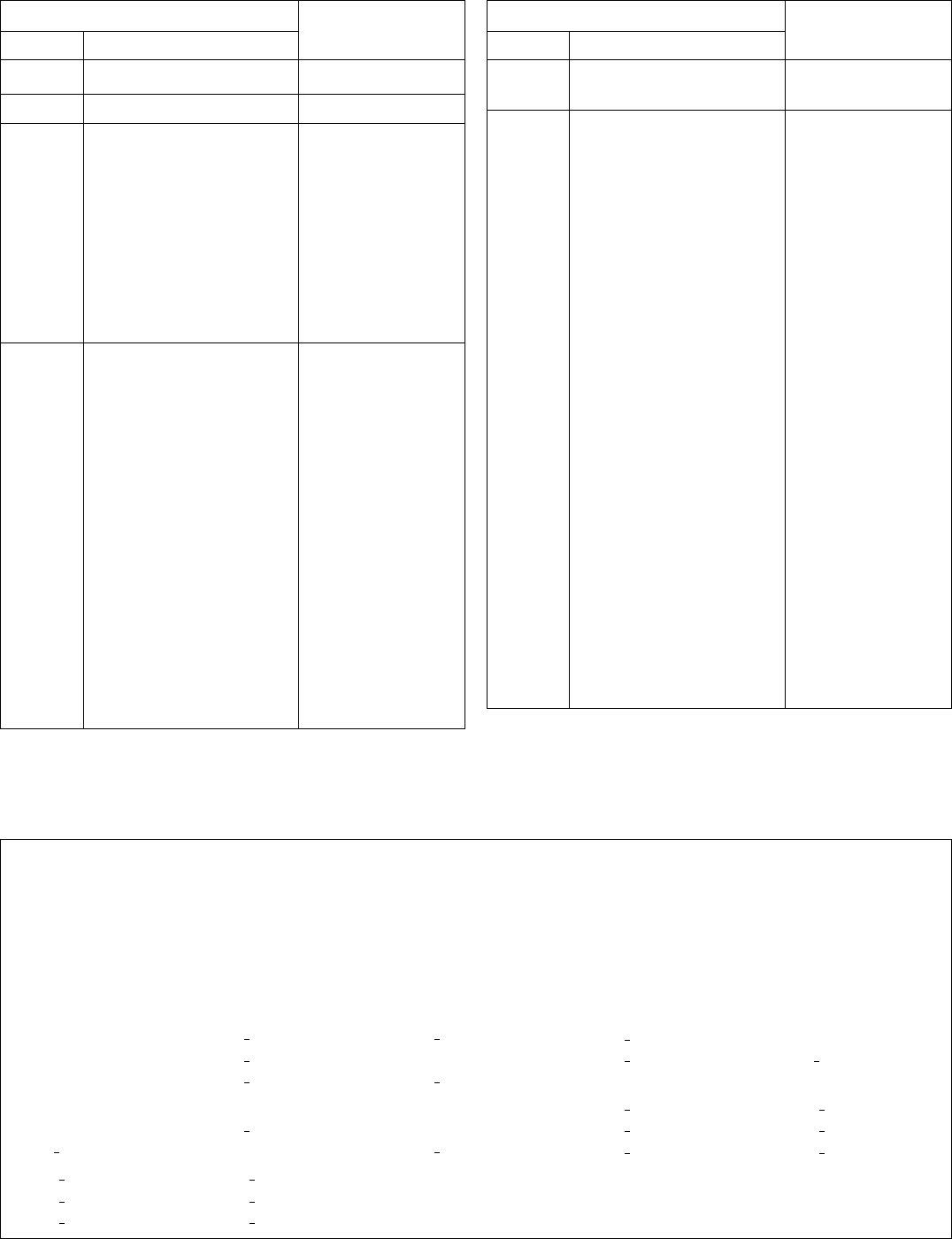
Table 15.2.2.1. Affine normalizers of the triclinic and monoclinic space groups
Space group G
Matrix–vector pairs in
Table 15.2.2.2
No. Hermann–Mauguin symbol
1 P1 M
1
, v
1
2 P
1 M
1
, v
2
3 P121 M
2
, v
3
3 P112 M
3
, v
4
4 P12
1
1 M
2
, v
3
4 P112
1
M
3
, v
4
5 C121 M
4
, v
3
5 A121 M
5
, v
3
5 I121 M
6
, v
3
; M
7
, v
3
5 A112 M
8
, v
4
5 B112 M
9
, v
4
5 I112 M
10
, v
4
; M
11
, v
4
6 P1m1 M
2
, v
5
6 P11m M
3
, v
6
7 P1c1 M
5
, v
5
7 P1n1 M
6
, v
5
; M
7
, v
5
7 P1a1 M
4
, v
5
7 P11a M
9
, v
6
7 P11n M
10
, v
6
; M
11
, v
6
7 P11b M
8
, v
6
8 C1m1 M
4
, v
5
8 A1m1 M
5
, v
5
8 I1m1 M
6
, v
5
; M
7
, v
5
8 A11m M
8
, v
6
8 B11m M
9
, v
6
8 I11m M
10
, v
6
; M
11
, v
6
9 C1c1 M
6
, v
5
; M
12
, v
7
9 A1n1 M
6
, v
5
; M
13
, v
7
9 I1a1 M
6
, v
5
; M
7
, v
7
9 A11a M
10
, v
6
; M
14
, v
8
Space group G
Matrix–vector pairs in
Table 15.2.2.2
No. Hermann–Mauguin symbol
9 B11n M
10
, v
6
; M
15
, v
8
9 I11b M
10
, v
6
; M
11
, v
8
10 P12/m1 M
2
, v
2
10 P112/m M
3
, v
2
11 P12
1
=m1 M
2
, v
2
11 P112
1
=m M
3
, v
2
12 C12/m1 M
4
, v
2
12 A12/m1 M
5
, v
2
12 I12/m1 M
6
, v
2
; M
7
, v
2
12 A112/m M
8
, v
2
12 B112/m M
9
, v
2
12 I112/m M
10
, v
2
; M
11
, v
2
13 P12/c1 M
5
, v
2
13 P12/n1 M
6
, v
2
; M
7
, v
2
13 P12/a1 M
4
, v
2
13 P112/a M
9
, v
2
13 P112/n M
10
, v
2
; M
11
, v
2
13 P112/b M
8
, v
2
14 P12
1
=c1 M
5
, v
2
14 P12
1
=n1 M
6
, v
2
; M
7
, v
2
14 P12
1
=a1 M
4
, v
2
14 P112
1
=a M
9
, v
2
14 P112
1
=n M
10
, v
2
; M
11
, v
2
14 P112
1
=b M
8
, v
2
15 C12/c1 M
6
, v
2
; M
12
, v
9
15 A12/n1 M
6
, v
2
; M
13
, v
10
15 I12/a1 M
6
, v
2
; M
7
, v
11
15 A112/a M
10
, v
2
; M
14
, v
10
15 B112/n M
10
, v
2
; M
15
, v
12
15 I112/b M
10
, v
2
; M
11
, v
11
Table 15.2.2.2. Matrices and vectors used in Table 15.2.2.1 for the description of the affine normalizers of monoclinic and
triclinic space groups
n, g and u represent integer, even and odd numbers, respectively, r, s and t real numbers. For all matrices, det M
i
1 must hold.
M
1
n
11
n
12
n
13
n
21
n
22
n
23
n
31
n
32
n
33
0
@
1
A
M
2
n
11
0 n
13
0 10
n
31
0 n
33
0
@
1
A
M
3
n
11
n
12
0
n
21
n
22
0
001
0
@
1
A
M
4
u
11
0 n
13
0 10
g
31
0 u
33
0
@
1
A
M
5
u
11
0 g
13
0 10
n
31
0 u
33
0
@
1
A
M
6
u
11
0 g
13
0 10
g
31
0 u
33
0
@
1
A
M
7
g
11
0 u
13
0 10
u
31
0 g
33
0
@
1
A
M
8
u
11
g
12
0
n
21
u
22
0
001
0
@
1
A
M
9
u
11
n
12
0
g
21
u
22
0
001
0
@
1
A
M
10
u
11
g
12
0
g
21
u
22
0
001
0
@
1
A
M
11
g
11
u
12
0
u
21
g
22
0
001
0
@
1
A
M
12
u
11
0 u
13
0 10
g
31
0 u
33
0
@
1
A
M
13
u
11
0 g
13
0 10
u
31
0 u
33
0
@
1
A
M
14
u
11
g
12
0
u
21
u
22
0
001
0
@
1
A
M
15
u
11
u
12
0
g
21
u
22
0
001
0
@
1
A
v
1
r
s
t
0
B
@
1
C
A
v
2
1
2
n
1
1
2
n
2
1
2
n
3
0
B
@
1
C
A
v
3
1
2
n
1
s
1
2
n
3
0
B
@
1
C
A
v
4
1
2
n
1
1
2
n
2
t
0
B
@
1
C
A
v
5
r
1
2
n
2
t
0
B
@
1
C
A
v
6
r
s
1
2
n
3
0
B
@
1
C
A
v
7
r
1
4
u
2
t
0
B
@
1
C
A
v
8
r
s
1
4
u
3
0
B
@
1
C
A
v
9
1
4
u
1
1
4
u
2
1
2
n
3
0
B
@
1
C
A
v
10
1
2
n
1
1
4
u
2
1
4
u
3
0
B
@
1
C
A
v
11
1
4
u
1
1
4
u
2
1
4
u
3
0
B
@
1
C
A
v
12
1
4
u
1
1
2
n
2
1
4
u
3
0
B
@
1
C
A
899
15.2. EUCLIDEAN AND AFFINE NORMALIZERS

15.3. Examples of the use of normalizers
BY E. KOCH AND W. FISCHER
15.3.1. Introduction
The Euclidean and the affine normalizers of a space group form the
appropriate tool to define equivalence relationships on sets of
objects that are not symmetrically equivalent in this space group but
‘play the same role’ with respect to this group. Two such objects
referring to the same space group will be called Euclidean- or
affine-equivalent if there exists a Euclidean or affine mapping that
maps the two objects onto one another and, in addition, maps the
space group onto itself.
15.3.2. Equivalent point configurations, equivalent
Wyckoff positions and equivalent descriptions of crystal
structures
In the crystal structure of copper, all atoms are symmetrically
equivalent with respect to space group Fm
3m. The pattern of Cu
atoms may be described equally well by Wyckoff position 4a 000
or 4b
1
2
1
2
1
2
. The Euclidean normalizer of Fm3m gives the relation
between the two descriptions.
Two point configurations (crystallographic orbits)* of a space
group G are called Euclidean-orN
E
-equivalent (affine-orN
A
-
equivalent) if they are mapped onto each other by the Euclidean
(affine) normalizer of G.
Affine-equivalent point configurations play the same role with
respect to the space-group symmetry, i.e. their points are embedded
in the pattern of symmetry elements in the same way. Euclidean-
equivalent point configurations are congruent and may be inter-
changed when passing from one descr iption of a crystal structure to
another.
Starting from any given point configuration of a space group G,
one may derive all Euclidean-equivalent point configurations and –
except for monoclinic and triclinic space groups – all affine-
equivalent ones by successive application of the ‘additional
generators’ of the normalizer as given in Tables 15.2.1.3 and
15.2.1.4.
Examples
(1) A point configuration F
43m 16e xxx with x
1
0:10 may be
visualized as a set of parallel tetrahedra arranged in a cubic face-
centred lattice. The Euclidean and affine normalizer of F
43m is
Im
3m with a
0
1
2
a (cf. Table 15.2.1.4). Since the index k
g
of G
in KG is 4, three additional equivalent point configurations
exist, which follow from the original one by repeated
application of the tabulated translation t
1
4
1
4
1
4
: 16e xxx with
x
2
0:35, x
3
0:60, x
4
0:85. LG differs from KG and an
additional centre of symmetry is located at 000. Accordingly,
the following four equivalent point configurations may be
derived from the first four: 16e xxx with x
5
0:10,
x
6
0:35, x
7
0:60, x
8
0:85. In this case, the index 8
of G in N
E
G equals the number of Euclidean-equivalent point
configurations.
(2) F
43m 4a 000 represents a face-centred cubic lattice. The
additional translations of KF
43m generate three equivalent
point configurations: 4c
1
4
1
4
1
4
,4b
1
2
1
2
1
2
and 4d
3
4
3
4
3
4
. Inversion
through 000 maps 4a and 4b each onto itself and interchanges 4c
and 4d. Therefore, here the number of equivalent point
configurations is four, i.e. only half the index of G in N
E
G.
The difference between the two examples is the following: The
reference point 0.1, 0.1, 0.1 of the first example does not change its
site symmetry .3m when passing from F
43m to Im3m. Point 000 of
the second example, however, has site symmetry
43m in F43m, but
m
3m in Im3m.
The following rule holds without exception: The number of point
configurations equivalent to a given one is equal to the quotient i=i
s
,
with i being the subgroup index of G in its Euclidean or affine
normalizer and i
s
the subgroup index between the corresponding
two site-symmetry groups of any point in the original point
configuration.
As a necessary but not sufficient condition for i
s
6 1 when
referring to the Euclidean normalizer, the inherent symmetry
(eigensymmetry) of the point configuration considered (i.e. the
group of all motions that maps the point configuration onto itself)
must be a proper supergroup of G.IfD designates the intersection
group of N
E
G with the inherent symmetry of the point
configuration, the number of Euclidean-equivalent point configura-
tions equals the index of D in N
E
G.
Example
The Euclidean and affine normalizer of P2
1
3isIa3d with index
8. Point configuration 4a xxx with x
1
0 forms a face-centred
cubic lattice with inherent symmetry Fm
3m. The reference point
000 has site symmetry .3. in P2
1
3 but :3: in Ia3d. The number of
equivalent point configurations, therefore, is i=i
s
8= 2 4. One
additional point configuration is generated by the translation
t
1
2
1
2
1
2
: 4a xxx with x
2
1
2
, the two others by applying the
d-glide reflection y
1
4
, x
1
4
, z
1
4
to the first two point
configurations: 4a xxx with x
3
1
4
and x
4
3
4
. The intersection
group D of the inherent symmetry Fm
3m with the normalizer
Ia
3d is Pa3. Its index 4 in Ia3d gives again the number of
equivalent point configurations.
The set of equivalent point configurations is always infinite if the
normalizer contains continuous translations but this set may be
described by a finite number of subsets due to non-continuous
translations.
Example
The Euclidean and affine normalizer of P6
1
is P
1
622 (a, b, "c).
With the aid of the ‘additional generators’ given in Table
15.2.1.4, one can calculate two subsets of point configurations
that are equivalent to a given general point configuration 6a xyz
with x x
0
, y y
0
, z z
0
:6a xyz with x
0
, y
0
, z
0
t and
y
0
, x
0
, z
0
t. If, however, the coordinates for the original
point configuration are specialized, e.g. to x y x
1
, z z
1
or
to x y 0, z z
2
, only one subset exists, namely x
1
, x
1
, z
1
t
or 0, 0, z
2
t, respectively. The reduction of the number of
subsets is a consequence of the enhancement of the site
symmetry in the normalizer (.2. or 622, respectively), but the
index i
s
, as introduced above, does not necessarily give the
reduction factor for the number of subsets.
It has to be noticed that for most space groups with a Euclidean
normalizer containing continuous translations the index i
s
is larger
than 1 for all point configurations, i.e. the number of subsets of
equivalent point configurations is necessarily reduced. The general
Wyckoff position of such a space group does not belong to a
*
For the use of the terms ‘point configuration’ and ‘crystallographic orbit’ see
Koch & Fischer (1985).
900
International Tables for Crystallography (2006). Vol. A, Chapter 15.3, pp. 900–903.
Copyright © 2006 International Union of Crystallography
