Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry
Подождите немного. Документ загружается.


Laue class of G.IfN
E
G is noncentrosymmetric, an intermediate
group LG cannot exist.
The groups KG and LG are of special interest in connection
with direct methods for structure determination: they cause the
parity classes of reflections; KG defines the permissible origin
shifts and the parameter ranges for the phase restrictions in the
specification of the origin; and LG gives information on possible
phase restrictions for the selection of the enantiomorph. For any
space (plane) group G, the translation subgroups of KG, LG,
N
E
G and even N
A
G coincide.
The Euclidean normalizers of the plane groups are listed in Table
15.2.1.1, those of triclinic space groups in Table 15.2.1.2, of
monoclinic and orthorhombic space groups in Table 15.2.1.3, and
those of all other space groups in Table 15.2.1.4. Herein all settings
and choices of cell and origin as tabulated in Parts 6 and 7 are taken
into account and, in addition, all metrical specializations giving rise
to Euclidean normalizers with enhanced symmetry. Each setting,
cell choice, origin or metrical specialization corresponds to one line
in the tables. (Exceptions are some orthorhombic space groups with
tetragonal metric: if a b as well as b c and c a give rise to a
symmetry enhancement of the Euclidean normalizer, only the case
a b is listed in Table 15.2.1.3.)
The first column of Tables 15.2.1.1, 15.2.1.3 and 15.2.1.4 shows
the number of the plane group or space group, the second column
its Hermann–Mauguin symbol together with information on the
setting, cell choice and origin, if necessary. Special metrical
conditions affecting the Euclidean normalizer are tabulated in the
third column of Tables 15.2.1.1 and 15.2.1.3. The term ‘general’
means that only the general metrical conditions for the respective
crystal system are valid. In Table 15.2.1 .4, a corresp onding column
is superfluous because here a metrical specialization of the space
group does not influence the type of the Euclidean normalizer.
The Euclidean normalizer of the space (plane) group is identified
in the fourth column of Table 15.2.1.3 (15.2.1.1) or in the third
column of Table 15.2.1.4. As Euclidean normalizers are groups of
motions, they can normally be designated by Hermann–Mauguin
symbols. If, however, the origin of the space (plane) group is not
fixed by symmetry (examples: P4, P1m1, P1), the Euclidean
normalizer contains continuous translations in one, two or three
(one or two) independent directions. In these cases, P
1
, B
1
, C
1
, P
2
or
Table 15.2.1.1. Euclidean normalizers of the plane groups
For the restrictions of the cell metric of the two oblique plane groups see text and Fig. 15.2.1.3.
Plane group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of G in
N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Twofold
rotation
Further
generators
1 p1 General p
2
2 "
1
a, "
2
b r,0;0,s x, y 1
2
2 1
a < b, 90
p
2
2mm "
1
a, "
2
b r,0;0,s x, y x, y 1
2
2 2
2 cos a=b,90<<120
c
2
2mm "
1
a, "
2
1
2
a b r,0;0,s x, yx y, y 1
2
2 2
a b,90<<120
c
2
2mm "
1
a b, "
2
a b r,0;0,s x, yy, x 1
2
2 2
a b, 90
p
2
4mm "a, "b r,0;0,s x, y x, y; y, x 1
2
2 4
a b, 120
p
2
6mm "a, "b r,0;0,s x, yy, x; x, x y 1
2
2 6
2 p2 General p2
1
2
a,
1
2
b
1
2
,0; 0,
1
2
4 1 1
a < b, 90
p2mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
x, y 4 1 2
2 cos a=b,90<<120
c2mm
1
2
a,
1
2
a b
1
2
,0; 0,
1
2
x y, y 4 1 2
a b,90<<120
c2mm
1
2
a b,
1
2
a b
1
2
,0; 0,
1
2
y, x 4 1 2
a b, 90
p4mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
x, y; y, x 4 1 4
a b, 120
p6mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
y, x; x, x y 4 1 6
3 p1m1 p
1
2mm
1
2
a, "b
1
2
,0; 0,s x, y 2 12 1
4 p1g1 p
1
2mm
1
2
a, "b
1
2
,0; 0,s x, y 2 12 1
5 c1m1 p
1
2mm
1
2
a, "b 0, s x, y 12 1
6 p2mm a 6 bp2mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
4 1 1
a bp4mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
y, x 4 1 2
7 p2mg p2mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
4 1 1
8 p2gg a 6 bp2mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
4 1 1
a bp4mm
1
2
a,
1
2
b
1
2
,0; 0,
1
2
y, x 4 1 2
9 c2mm a 6 bp2mm
1
2
a,
1
2
b
1
2
,0 2 1 1
a bp4mm
1
2
a,
1
2
b
1
2
,0 y, x 2 1 2
10 p4 p4mm
1
2
a b,
1
2
a b
1
2
,
1
2
y, x 2 1 2
11 p4mm p4mm
1
2
a b,
1
2
a b
1
2
,
1
2
2 1 1
12 p4gm p4mm
1
2
a b,
1
2
a b
1
2
,
1
2
2 1 1
13 p3 p6mm
1
3
2a b,
1
3
a b
2
3
,
1
3
x, yy, x 3 2 2
14 p3m1 p6mm
1
3
2a b,
1
3
a b
2
3
,
1
3
x, y 3 2 1
15 p31mp6mm a, b x, y 1 2 1
16 p6 p6mm a, b y, x 1 1 2
17 p6mm p6mm a, b 1 1 1
881
15.2. EUCLIDEAN AND AFFINE NORMALIZERS

P
3
(p
1
, c
1
, p
2
), respectively, are used instead of the Bravais letter.*
Setting and origin choice for the Euclidean normalizers are
indicated as for space groups. In a few cases, origin choices not
tabulated in Part 7 are needed.
In the next column, the basis of N
E
Gis described in terms of the
basis of G. A factor " is used to indicate continuous translations.
The following three columns specify a set of additional
symmetry operations that generate KG , LG and N
E
G
successively from the space group G: The first of them shows the
vector components of the additional translations generating KG
from G; components referring to continuous translations are labelled
r, s and t .IfLG differs from KG, i.e. if G is noncentrosymmetric
and N
E
G is centrosymmetric, the position of an additional centre
of symmetry is given in the second of these columns. The respective
inversion generates LG from KG. (For plane groups, additional
twofold rotations play the role of these inversions.) If, however,
N
E
G is noncentrosymmetric and, therefore, LG is undefined,
this fact is indicated by a slash. The last of these columns contains
entries only if G and N
E
G belong to different Laue classes. The
corresponding additional generators are listed as coordinate triplets.
In the last column, the subgroup index of G in N
E
G is specified
as the product k
g
l
k
n
l
, where k
g
means the index of G in KG, l
k
the
index of KG in LG and n
l
the index of LG in N
E
G. [In the
case of a noncentrosymmetric normalizer, the index of G in N
E
G
is given as the product k
g
n
k
, where k
g
means the index of G in KG
and n
k
the index of KG in N
E
G.] For continuous translations, k
g
is always infinite. Nevertheless, it is useful to distinguish different
cases: 1, 1
2
and 1
3
refer to one, two and three independent
directions with continuous translations. An additional factor of 2
n
or
3
n
indicates the existence of n additional independent translations
which are not continuous.
For triclinic space groups, each metrical specialization gives rise
to a symmetry enhancement of the Euclidean normalizer. The
corresponding conditions for the metrical parameters, however,
cannot be described as easily as in the monoclinic case (for further
information see Part 9 and literature on ‘reduced cells’ cited
therein). Table 15.2.1.2 shows the Euclidean normalizers for P1 and
P
1. Each special metrical condition is designated by the Bravais
type of the corresponding translation lattice. In the case of P
1, the
Euclidean normalizer is always the inherent symmetry group of a
suitably chosen point lattice with basis vectors
1
2
a
c
,
1
2
b
c
and
1
2
c
c
.
Here, a
c
, b
c
and c
c
do not refer to the primitive unit cell of P1 but to
the possibly centred conventional cell for the respective Bravais
lattice. In the case of P1, the Euclidean normalizer always contains
continuous translations in three independent directions, symbolized
by P
3
. These normalizers may be easily derived from those for P
1.
15.2.2. Affine normalizers of plane groups and space
groups
The affine normalizer N
A
G of a space (plane) group G either is a
true supergroup of its Euclidean normalizer N
E
G, or both
normalizers coincide:
N
A
G N
E
G:
As any translation is an isometry, each translation belonging to
N
A
G also belongs to N
E
G. Therefore, the affine normalizer and
the Euclidean normalizer of a space (plane) group necessarily have
identical translation subgroups.
By analogy to the isometries of the Euclidean normalizer, the
additional mappings of the affine normalizer also map the set of all
symmetry elements of the space (plane) group onto itself .
In contrast to the Euclidean normalizers, the affine normalizers of
all space (plane) groups of a certain type belong to only one type
of normalizer, i.e. they are isomorphic groups. Therefore, the type
of the affine normalizer N
A
G never depends on the metrical
properties of the space group G.
If for all space (plane) groups of a certain type the Euclidean
normalizers also belong to one type, then for each such space
(plane) group the Euclidean and the affine normalizers are identical,
irrespective of any metrical specialization, i.e. N
E
G N
A
G
holds. Then, the affine normalizers are pure groups of motions and
do not contain any further affine mappings. This is true for all cubic,
hexagonal, trigonal and tetragonal space groups (for all hexagonal
and square plane groups) and, in addition, for the space groups of 21
further orthorhombic types (plane groups of 2 further rectangular
types) [examples: N
A
PccaPmmm, N
A
Pnc2P
1
mmm].
For each of the other 38 types of orthorhombic space group (5
types of rectangular plane groups), the type of the affine norm alizer
corresponds to the type of the highest-symmetry Euclidean
normalizers belonging to that space (plane)-group type. Therefore,
it may also be symbolized by (possibly modified) Hermann–
Mauguin symbols [examples: N
A
PbcaPm3, N
A
Pccn
P4=mmm, N
A
Pcc2P
1
4=mmm].
As the affine normalizer of a monoclinic or triclinic space group
(oblique plane group) is not isomorphic to any group of motions, it
cannot be characterized by a modified Hermann–Mauguin symbol.
It may be described, however, by one or two matrix–vector pairs
together with the appropriate restrictions on the coefficients. Similar
information has been given by Billiet et al. (1982) for the standard
description of each group. The problem has been discussed in more
detail by Gubler (1982a,b).
In Table 15.2.2.1, the affine normalizers of all triclinic and
monoclinic space groups are given. The first two columns
correspond to those of Table 15.2.1.3 or 15.2.1.4. The affine
normalizers are completely described in column 3 by one or two
general matrix–vector pairs. All unimodular matrices and vectors
used in Table 15.2.2.1 are listed explicitly in Table 15.2.2.2. The
matrix–vector representation of an affine normalizer consists of all
Table 15.2.1.2. Euclidean normalizers of the triclinic space
groups
Basis vectors of the Euclidean normalizers (a
c
, b
c
, c
c
refer to the possibly
centred conventional unit cell for the respective Bravais lattice):
P1 : "a
c
, "b
c
, "c
c
; P
1 :
1
2
a
c
,
1
2
b
c
,
1
2
c
c
.
Euclidean normalizer N
E
G of
Bravais type 1 P12 P
1
aP P
3
1 P
1
mP P
3
2=mP2=m
mA P
3
2=mA2=m
oP P
3
mmm Pmmm
oC P
3
mmm Cmmm
oF P
3
mmm Fmmm
oI P
3
mmm Immm
tP P
3
4=mmm P4=mmm
tI P
3
4=mmm I4=mmm
hP P
3
6=mmm P6=mmm
hR P
3
3m1 R
3m
cP P
3
m
3mPm
3m
cF P
3
m
3mFm
3m
cI P
3
m
3mIm
3m
(continued on page 894)
*
In the previous editions, the symbols Z
1
, Z
2
and Z
3
z
1
, z
2
were used.
882
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY
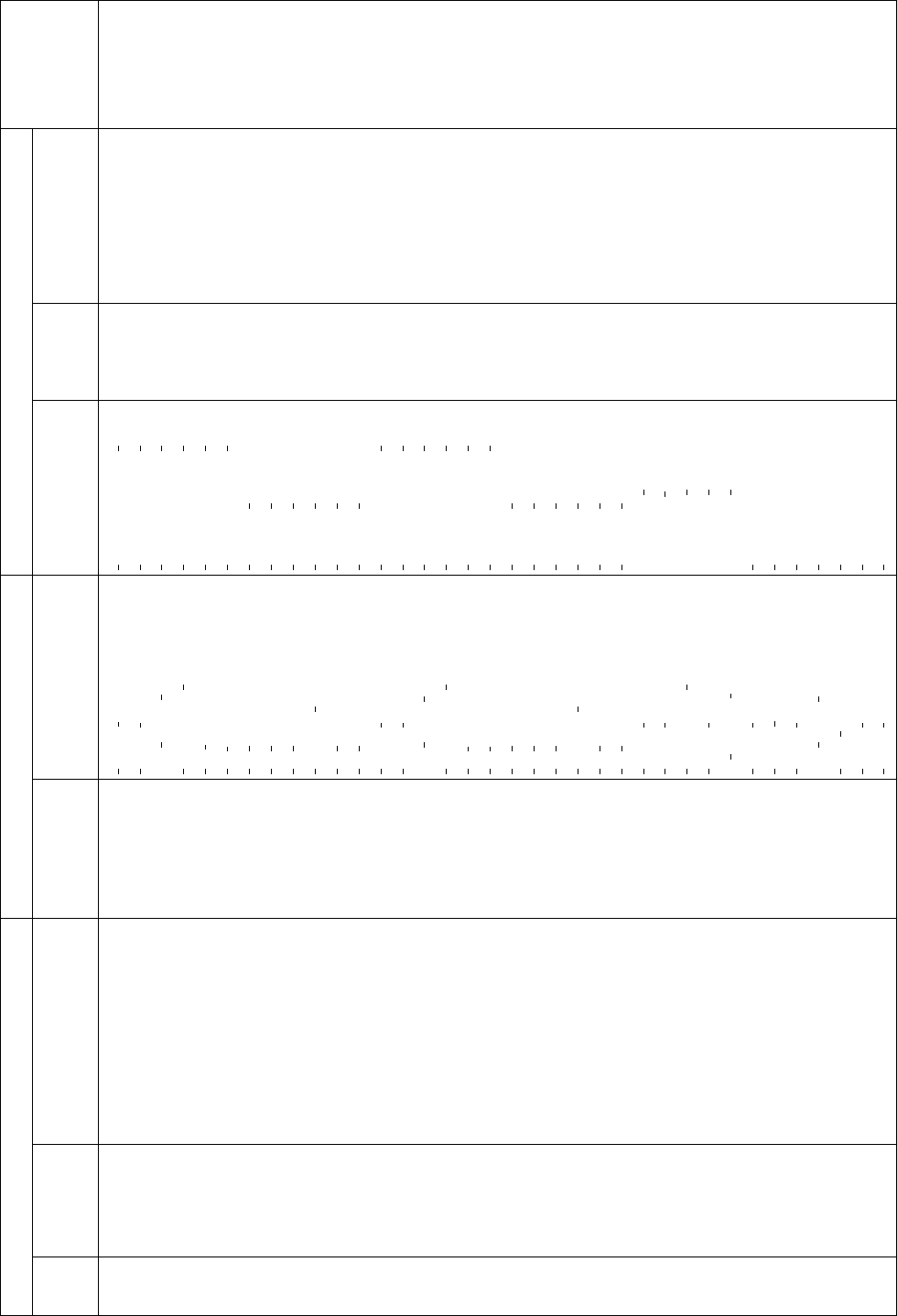
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups
For the restrictions of the cell metric of monoclinic space groups see text and Figs. 15.2.1.1 to 15.2.1.4. The symbols in parentheses following a space-group symbol refer to the location of the origin (‘origin choice’ in
Part 7).
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
3 P121 General P
1
12=m1
1
2
a, "b,
1
2
c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 4 12 1
a>c, 90
P
1
mmm
1
2
a, "b,
1
2
c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z 4 12 2
2 cos c=a,90<<120
B
1
mmm a
1
2
c, "b,
1
2
c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 x, y, x z 4 12 2
a c,90<<120
B
1
mmm
1
2
a c, "b,
1
2
a c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 z, y, x 4 12 2
a c, 90
P
1
4=mmm
1
2
c,
1
2
a, "b
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z; z, y, x 4 12 4
a c, 120
P
1
6=mmm
1
2
c,
1
2
a, "b
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 z, y, x;
x z, y, z 4 12 6
3 P112 General P
1
112=m
1
2
a,
1
2
b, "c,
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
a<b, 90
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z 4 12 2
2 cos a=b,90<<120
C
1
mmm
1
2
a,
1
2
a b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x y, y, z 4 12 2
a b,90<<120
C
1
mmm
1
2
a b,
1
2
a b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z 4 12 2
a b, 90
P
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z; y, x, z 4 12 4
a b, 120
P
1
6=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z; x, x y, z 4 12 6
4 P12
1
1 General P
1
12=m1
1
2
a, "b,
1
2
c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 4 12 1
a>c, 90
P
1
mmm
1
2
a, "b,
1
2
c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z 4 12 2
2 cos c=a,90<<120
B
1
mmm a
1
2
c, "b,
1
2
c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 x, y, x z 4 12 2
a c,90<<120
B
1
mmm
1
2
a c, "b,
1
2
a c
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 z, y, x 4 12 2
a c, 90
P
1
4=mmm
1
2
c,
1
2
a, "b
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z; z, y, x 4 12 4
a c, 120
P
1
6=mmm
1
2
c,
1
2
a, "b
1
2
,0,0;0,s,0;0,0,
1
2
0, 0, 0 z, y, x;
x z, y, z 4 12 6
4 P112
1
General P
1
112=m
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 4 12 1
a<b, 90
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z 4 12 2
2 cos a=b,90<<120
C
1
mmm
1
2
a,
1
2
a b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x y, y, z 4 12 2
a b,90<<120
C
1
mmm
1
2
a b,
1
2
a b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z 4 12 2
a b, 90
P
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z; y, x, z 4 12 4
a b, 120
P
1
6=mmm
1
2
a,
1
2
b, "c
1
2
,0,0;0,
1
2
,0;0,0,t 0, 0, 0 y, x, z; x, x y, z 4 12 6
5 C121 General P
1
12=m1
1
2
a, "b,
1
2
c 0, s,0; 0,0,
1
2
0, 0, 0 2 12 1
90
P
1
mmm
1
2
a, "b,
1
2
c 0, s,0;0,0,
1
2
0, 0, 0
x, y, z 2 12 2
cos c=a,90<<135
P
1
mmm
1
2
a c, "b,
1
2
c 0, s,0; 0,0,
1
2
0, 0, 0 x, y,2x z 2 12 2
2 cos a=c,90<<135
B
1
mmm
1
2
a, "b,
1
2
a c 0, s,0; 0,0,
1
2
0, 0, 0
x z, y, z 2 12 2
a c
2
p
, 135
P
1
4=mmm
1
2
a c,
1
2
c, "b 0, s,0; 0,0,
1
2
0, 0, 0 x, y,2x z;
x z, y, z 2 12 4
5 A121 General P
1
12=m1
1
2
a, "b,
1
2
c
1
2
,0,0; 0,s, 0 0, 0, 0 2 12 1
90
P
1
mmm
1
2
a, "b,
1
2
c
1
2
,0,0; 0,s, 0 0, 0, 0
x, y, z 2 12 2
cos a=c,90<<135
P
1
mmm
1
2
a, "b,
1
2
a c
1
2
,0,0; 0,s, 0 0, 0, 0
x 2z, y, z 2 12 2
2 cos c=a,90<<135
B
1
mmm a
1
2
c, "b,
1
2
c
1
2
,0,0; 0,s, 0 0, 0, 0 x, y, x z 2 12 2
c a
2
p
, 135
P
1
4=mmm
1
2
a,
1
2
a c, "b
1
2
,0,0; 0,s, 0 0, 0, 0 x, y, x z;
x 2z, y, z 2 12 4
5 I121 General P
1
12=m1
1
2
a, "b,
1
2
c
1
2
,0,0; 0,s, 0 0, 0, 0 2 12 1
a>c, 90
P
1
mmm
1
2
a, "b,
1
2
c
1
2
,0,0; 0,s, 0 0, 0, 0
x, y, z 2 12 2
883
15.2. EUCLIDEAN AND AFFINE NORMALIZERS
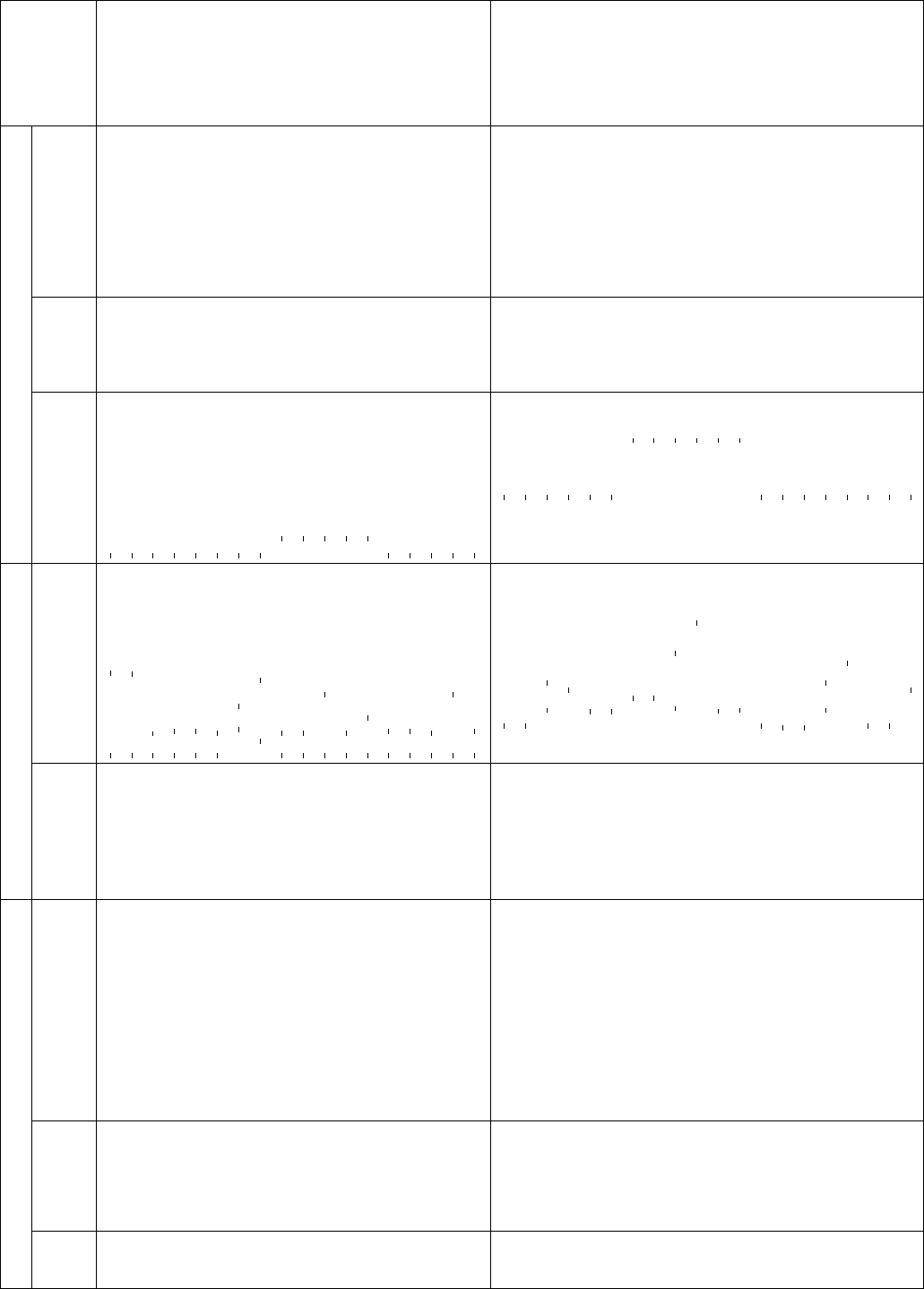
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
cos c=a,90<<180
P
1
mmm
1
2
a c, "b,
1
2
c
1
2
,0,0; 0,s, 0 0, 0, 0 x, y,2x z 2 12 2
a c,90<<180
B
1
mmm
1
2
a c, "b,
1
2
a c
1
2
,0,0; 0,s, 0 0, 0, 0 z, y, x 2 12 2
a c, 90
P
1
4=mmm
1
2
c,
1
2
a, "b
1
2
,0,0; 0,s, 0 0, 0, 0
x, y, z; z, y, x 2 12 4
5 A112 General P
1
112=m
1
2
a,
1
2
b, "c
1
2
,0,0; 0,0,t 0, 0, 0 2 12 1
90
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0; 0,0,t 0, 0, 0
x, y, z 2 12 2
cos a=b,90<<135
P
1
mmm
1
2
a,
1
2
a b, "c
1
2
,0,0; 0,0,t 0, 0, 0 x 2y, y, z 2 12 2
2 cos b=a,90<<135
C
1
mmm a
1
2
b,
1
2
b, "c
1
2
,0,0; 0,0,t 0, 0, 0 x, x y, z 2 12 2
b a
2
p
, 135
P
1
4=mmm
1
2
a b,
1
2
a, "c
1
2
,0,0; 0,0,t 0, 0, 0
x 2y, y, z; x, x y, z 2 12 4
5 B112 General P
1
112=m
1
2
a,
1
2
b, "c 0,
1
2
,0;0,0,t 0, 0, 0 2 12 1
90
P
1
mmm
1
2
a,
1
2
b, "c 0,
1
2
,0;0,0,t 0, 0, 0
x, y, z 2 12 2
cos b=a,90<<135
P
1
mmm
1
2
a b,
1
2
b, "c 0,
1
2
,0; 0,0,t 0, 0, 0 x,2x y, z 2 12 2
2 cos a=b,90<<135
C
1
mmm
1
2
a,
1
2
a b, "c 0,
1
2
,0; 0,0,t 0, 0, 0
x y, y, z 2 12 2
a b
2
p
, 135
P
1
4=mmm
1
2
b,
1
2
a b, "c 0,
1
2
,0; 0,0,t 0, 0, 0 x,2x y, z;
x y, y, z 2 12 4
5 I112 General P
1
112=m
1
2
a,
1
2
b, "c
1
2
,0,0; 0,0,t 0, 0, 0 2 12 1
a<b, 90
P
1
mmm
1
2
a,
1
2
b, "c
1
2
,0,0; 0,0,t 0, 0, 0
x, y, z 2 12 2
cos a=b,90<<180
P
1
mmm
1
2
a,
1
2
a b, "c
1
2
,0,0; 0,0,t 0, 0, 0
x 2y, y, z 2 12 2
a b,90<<180
C
1
mmm
1
2
a b,
1
2
a b, "c
1
2
,0,0; 0,0,t 0, 0, 0 y, x, z 2 12 2
a b, 90
P
1
4=mmm
1
2
a,
1
2
b, "c
1
2
,0,0; 0,0,t 0, 0, 0
x, y, z; y, x, z 2 12 4
6 P1m1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 2 1
2
2 1
a>c, 90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z 2 1
2
2 2
2 cos c=a,90<<120
P
2
mmm "
1
a
1
2
c,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 x, y, x z 2 1
2
2 2
a c,90<<120
P
2
mmm "
1
a c,
1
2
b, "
2
a c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 z, y, x 2 1
2
2 2
a c, 90
P
2
4=mmm "c, "a,
1
2
b r,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z; z, y, x 2 1
2
2 4
a c, 120
P
2
6=mmm "c, "a,
1
2
b r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 z, y, x;
x z, y, z 2 1
2
2 6
6 P11m General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 2 1
2
2 1
a<b, 90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z 2 1
2
2 2
2 cos a=b,90<<120
P
2
mmm "
1
a, "
2
1
2
a b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x y, y, z 2 1
2
2 2
a b,90<<120
P
2
mmm "
1
a b, "
2
a b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 y, x, z 2 1
2
2 2
a b, 90
P
2
4=mmm "a, "b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z; y, x, z 2 1
2
2 4
a b, 120
P
2
6=mmm "a, "b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 y, x, z; x, x y, z 2 1
2
2 6
7 P1c1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 2 1
2
2 1
90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z 2 1
2
2 2
cos a=c,90<<135
P
2
mmm "
1
a,
1
2
b, "
2
a c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x 2z, y, z 2 1
2
2 2
2 cos c=a,90<<135
P
2
mmm "
1
a
1
2
c,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 x, y, x z 2 1
2
2 2
c a
2
p
, 135
P
2
4=mmm "a, "a c,
1
2
b r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 x, y, x z;
x 2z, y, z 2 1
2
2 4
7 P1n1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0; 0,
1
2
,0;0,0,t 0, 0, 0 2 1
2
2 1
a>c, 90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,
1
2
,0; 0, 0, t 0, 0, 0
x, y, z 2 1
2
2 2
cos c=a,90<<180
P
2
mmm "
1
a c,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 x, y,2x z 2 1
2
2 2
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
884
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY

Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
a c,90<<180
P
2
mmm "
1
a c,
1
2
b, "
2
a c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 z, y, x 2 1
2
2 2
a c, 90
P
2
4=mmm "c, "a,
1
2
b r,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z; z, y, x 2 1
2
2 4
7 P1a1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 2 1
2
2 1
90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0
x, y, z 2 1
2
2 2
cos c=a,90<<135
P
2
mmm "
1
a c,
1
2
b, "
2
c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 x, y,2x z 2 1
2
2 2
2 cos a=c,90<<135
P
2
mmm "
1
a,
1
2
b, "
2
1
2
a c r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 x z, y , z 2 1
2
2 2
a c
2
p
, 135
P
2
4=mmm "a c, "c,
1
2
b r,0,0;0,
1
2
,0;0,0,t 0, 0, 0 x, y,2x z;
x z, y, z 2 1
2
2 4
7 P11a General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 2 1
2
2 1
90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z 2 1
2
2 2
cos b=a,90<<135
P
2
mmm "
1
a b, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 x,2x y, z 2 1
2
2 2
2 cos a=b,90<<135
P
2
mmm "
1
a, "
2
1
2
a b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x y, y, z 2 1
2
2 2
a b
2
p
, 135
P
2
4=mmm "b, "a b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 x,2x y, z; x y,
y, z 2 1
2
2 4
7 P11n General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 2 1
2
2 1
a<b, 90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 x, y, z 2 1
2
2 2
cos a=b,90<<180
P
2
mmm "
1
a, "
2
a b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x 2y, y, z 2 1
2
2 2
a b,90<<180
P
2
mmm "
1
a b, "
2
a b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 y, x, z 2 1
2
2 2
a b, 90
P
2
4=mmm "a, "b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z; y, x, z 2 1
2
2 4
7 P11b General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 2 1
2
2 1
90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x, y, z 2 1
2
2 2
cos a=b,90<<135
P
2
mmm "
1
a, "
2
a b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0
x 2y, y, z 2 1
2
2 2
2 cos b=a,90<<135
P
2
mmm "
1
a
1
2
b, "
2
b,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 x, x y, z 2 1
2
2 2
b a
2
p
, 135
P
2
4=mmm "a b, "a,
1
2
c r,0,0;0,s,0;0,0,
1
2
0, 0, 0 x 2y, y, z; x, x y, z 2 1
2
2 4
8 C1m1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0
x, y, z 1
2
2 2
cos c=a,90<<135
P
2
mmm "
1
a c,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 x, y,2x z 1
2
2 2
2 cos a=c,90<<135
P
2
mmm "
1
a,
1
2
b, "
2
1
2
a c r,0,0;0,0,t 0, 0, 0
x z, y, z 1
2
2 2
a c
2
p
, 135
P
2
4=mmm "a c, "c,
1
2
b r,0,0;0,0,t 0, 0, 0 x, y,2x z;
x z, y, z 1
2
2 4
8 A1m1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0
x, y, z 1
2
2 2
cos a=c,90<<135
P
2
mmm "
1
a,
1
2
b, "
2
a c r,0,0;0,0,t 0, 0, 0 x 2z, y, z 1
2
2 2
2 cos c=a,90<<135
P
2
mmm "
1
a
1
2
c,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 x, y, x z 1
2
2 2
c a
2
p
, 135
P
2
4=mmm "a, "a c,
1
2
b r,0,0;0,0,t 0, 0, 0 x, y, x z;
x 2z, y, z 1
2
2 4
8 I1m1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 1
2
2 1
a>c, 90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0
x, y, z 1
2
2 2
cos c=a,90<<180
P
2
mmm "
1
a c,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 x, y,2x z 1
2
2 2
a c,90<<180
P
2
mmm "
1
a c,
1
2
b, "
2
a c r,0,0;0,0,t 0, 0, 0 z, y, x 1
2
2 2
a c, 90
P
2
4=mmm "
1
c, "
2
a,
1
2
b r,0,0;0,0,t 0, 0, 0
x, y, z; z, y, x 1
2
2 4
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
885
15.2. EUCLIDEAN AND AFFINE NORMALIZERS
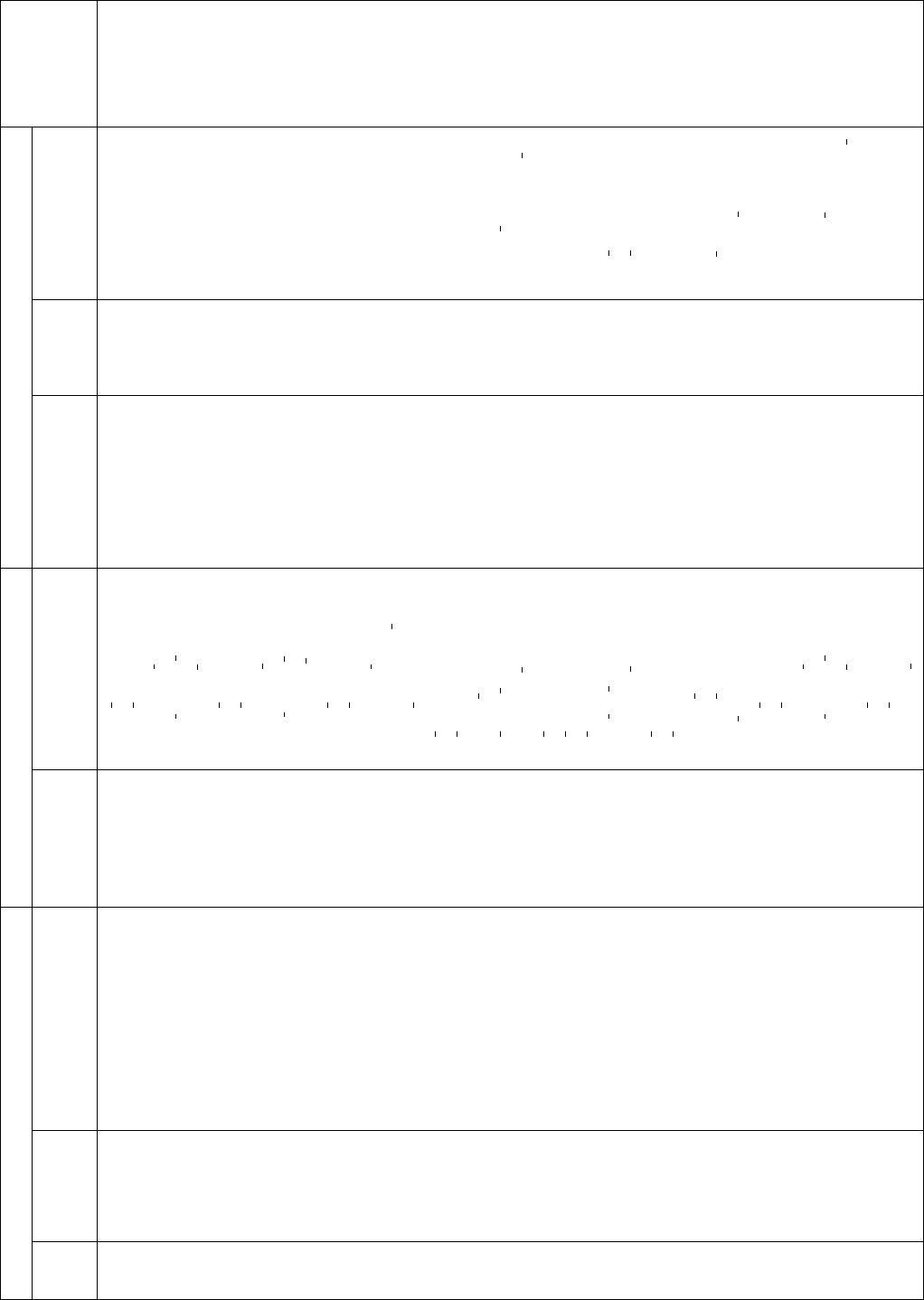
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
8 A11m General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z 1
2
2 2
cos a=b,90<<135
P
2
mmm "
1
a, "
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x 2y, y, z 1
2
2 2
2 cos b=a,90<<135
P
2
mmm "
1
a
1
2
b, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 x, x y , z 1
2
2 2
b a
2
p
, 135
P
2
4=mmm "a b, "a,
1
2
c r,0,0;0,s, 0 0, 0, 0
x 2y, y, z; x, x y, z 1
2
2 4
8 B11m General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z 1
2
2 2
cos b=a,90<<135
P
2
mmm "
1
a b, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 x,2x y, z 1
2
2 2
2 cos a=b,90<<135
P
2
mmm "
1
a, "
2
1
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x y, y, z 1
2
2 2
a b
2
p
, 135
P
2
4=mmm "
2
b, "a b,
1
2
c r,0,0;0,s, 0 0, 0, 0 x,2x y, z;
x y, y, z 1
2
2 4
8 I11m General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 1
2
2 1
a<b, 90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z 1
2
2 2
cos a=b,90<<180
P
2
mmm "
1
a, "
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x 2y, y, z 1
2
2 2
a b,90<<180
P
2
mmm "
1
a b, "
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0 y, x, z 1
2
2 2
a b, 90
P
2
4=mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z; y, x, z 1
2
2 4
9 C1c1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0
x, y, z 1
2
2 2
cos c=a,90<<135
P
2
mmm "
1
a c,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 x, y,2x z 1
2
2 2
2 cos a=c,90<<135
P
2
bmb "
1
a,
1
2
b, "
2
1
2
a c r,0,0;0,0,t 0, 0, 0
x z, y
1
4
, z 1
2
2 2
a c
2
p
, 135
P
2
4
2
=mmc "a c, "c,
1
2
b r,0,0;0,0,t 0, 0, 0 x, y,2x z;
x z, y
1
4
, z 1
2
2 4
9 A1n1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 x , y, z 1
2
2 2
cos a=c,90<<135
P
2
mmm "
1
a,
1
2
b, "
2
a c r,0,0;0,0,t 0, 0, 0
x 2z, y, z 1
2
2 2
2 cos c=a,90<<135
P
2
bmb "
1
a
1
2
c,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 x, y
1
4
, x z 1
2
2 2
c a
2
p
, 135
P
2
4
2
=mmc " a, "a c,
1
2
b r,0,0;0,0,t 0, 0, 0 x, y
1
4
, x z;
x 2z, y, z 1
2
2 4
9 I1a1 General P
2
12=m1 "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 1
2
2 1
a>c, 90
P
2
mmm "
1
a,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0
x, y, z 1
2
2 2
cos c=a,90<<180
P
2
mmm "
1
a c,
1
2
b, "
2
c r,0,0;0,0,t 0, 0, 0 x, y,2x z 1
2
2 2
a c,90<<180
P
2
bmb "
1
a c,
1
2
b, "
2
a c r,0,0;0,0,t 0, 0, 0 z, y
1
4
, x 1
2
2 2
a c, 90
P
2
4
2
=mmc " c, "a,
1
2
b r ,0,0;0,0,t 0, 0, 0 x, y , z; z, y
1
4
, x 1
2
2 4
9 A11a General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z 1
2
2 2
cos a=b,90<<135
P
2
mmm "
1
a, "
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x 2y, y, z 1
2
2 2
2 cos b=a,90<<135
P
2
ccm "
1
a
1
2
b, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 x, x y , z
1
4
1
2
2 2
b a
2
p
, 135
P
2
4
2
=mmc "a b, "a,
1
2
c r,0,0;0,s, 0 0, 0, 0
x 2y, y, z; x, x y, z
1
4
1
2
2 4
9 B11n General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 1
2
2 1
90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z 1
2
2 2
cos b=a,90<<135
P
2
mmm "
1
a b, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 x,2x y, z 1
2
2 2
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
886
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY

Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
2 cos a=b,90<<135
P
2
ccm "
1
a, "
2
1
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x y, y, z
1
4
1
2
2 2
a b
2
p
, 135
P
2
4
2
=mmc " b, "a b,
1
2
c r,0,0;0,s, 0 0, 0, 0 x,2x y, z;
x y, y, z
1
4
1
2
2 4
9 I11b General P
2
112=m "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0 1
2
2 1
a<b, 90
P
2
mmm "
1
a, "
2
b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z 1
2
2 2
cos a=b,90<<180
P
2
mmm "
1
a, "
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x 2y, y, z 1
2
2 2
a b,90<<180
P
2
ccm "
1
a b, "
2
a b,
1
2
c r,0,0;0,s, 0 0, 0, 0 y, x, z
1
4
1
2
2 2
a b, 90
P
2
4
2
=mmc " a, "b,
1
2
c r,0,0;0,s, 0 0, 0, 0
x, y, z; y, x, z
1
4
1
2
2 4
10 P12=m1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a>c, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
2 cos c=a,90<<120
Bmmm a
1
2
c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, x z 8 1 2
a c,90<<120
Bmmm
1
2
a c,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, y, x 8 1 2
a c, 90
P4=mmm
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; z, y, x 8 1 4
a c, 120
P6=mmm
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, y, x;
x z, y, z 8 1 6
10 P112=m General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a<b, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
2 cos a=b,90<<120
Cmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x y, y, z 8 1 2
a b,90<<120
Cmmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
a b, 90
P4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; y, x, z 8 1 4
a b, 120
P6=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z; x, x y, z 8 1 6
11 P12
1
=m1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a>c, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
2 cos c=a,90<<120
Bmmm a
1
2
c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, x z 8 1 2
a c,90<<120
Bmmm
1
2
a c,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, y, x 8 1 2
a c, 90
P4=mmm
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; z, y, x 8 1 4
a c, 120
P6=mmm
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, y, x;
x z, y, z 8 1 6
11 P112
1
=m General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a<b, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
2 cos a=b,90<<120
Cmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x y, y, z 8 1 2
a b,90<<120
Cmmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
a b, 90
P4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; y, x, z 8 1 4
a b, 120
P6=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z; x, x y, z 8 1 6
12 C12=m1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
x, y, z 4 1 2
cos c=a,90<<135
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
x, y,2x z 4 1 2
2 cos a=c,90<<135
Bmmm
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,0,
1
2
x z, y, z 4 1 2
a c
2
p
, 135
P4=mmm
1
2
a c,
1
2
c,
1
2
b
1
2
,0,0;0,0,
1
2
x, y,2x z;
x z, y, z 4 1 4
12 A12=m1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
887
15.2. EUCLIDEAN AND AFFINE NORMALIZERS
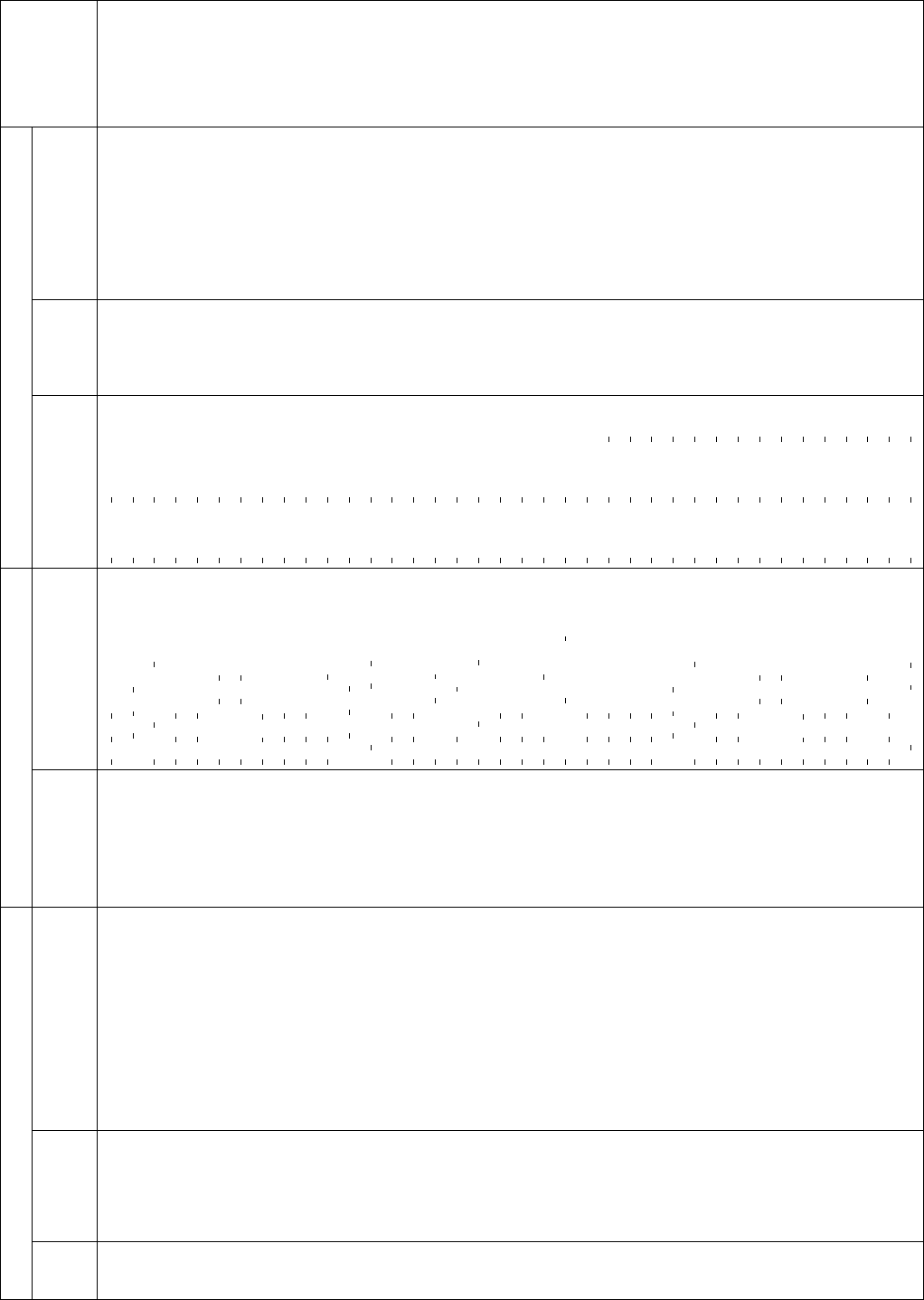
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
cos a=c,90<<135
Pmmm
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0
x 2z, y, z 4 1 2
2 cos c=a,90<<135
Bmmm a
1
2
c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x, y , x z 4 1 2
c a
2
p
, 135
P4=mmm
1
2
a,
1
2
a c,
1
2
b
1
2
,0,0;0,
1
2
,0 x, y , x z;
x 2z, y, z 4 1 4
12 I12=m1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a>c, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
cos c=a,90<<180
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x, y ,2x z 4 1 2
a c,90<<180
Bmmm
1
2
a c,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0 z, y, x 4 1 2
a c, 90
P4=mmm
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0
x, y, z; z, y, x 4 1 4
12 A112=m General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
cos a=b,90<<135
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0
x 2y, y, z 4 1 2
2 cos b=a,90<<135
Cmmm a
1
2
b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x, x y, z 4 1 2
b a
2
p
, 135
P4=mmm
1
2
a b,
1
2
a,
1
2
c
1
2
,0,0;0,
1
2
,0
x 2y, y, z; x, x y, z 4 1 4
12 B112=m General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
cos b=a,90<<135
Pmmm
1
2
a b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x,2x y, z 4 1 2
2 cos a=b,90<<135
Cmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0
x y, y, z 4 1 2
a b
2
p
, 135
P4=mmm
1
2
b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0 x,2x y, z;
x y, y, z 4 1 4
12 I112=m General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a<b, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
cos a=b,90<<180
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0
x 2y, y, z 4 1 2
a b,90<<180
Cmmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0 y, x, z 4 1 2
a b, 90
P4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z; y, x, z 4 1 4
13 P12=c1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos a=c,90<<135
Pmmm
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2z, y, z 8 1 2
2 cos c=a,90<<135
Bmmm a
1
2
c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, x z 8 1 2
c a
2
p
, 135
P4=mmm
1
2
a,
1
2
a c,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, x z;
x 2z, y, z 8 1 4
13 P12=n1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a>c, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos c=a,90<<180
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y,2x z 8 1 2
a c,90<<180
Bmmm
1
2
a c,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, y, x 8 1 2
a c, 90
P4=mmm
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; z, y, x 8 1 4
13 P12=a1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos c=a,90<<135
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y,2x z 8 1 2
2 cos a=c,90<<135
Bmmm
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x z, y, z 8 1 2
a c
2
p
, 135
P4=mmm
1
2
a c,
1
2
c,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y,2x z; x z, y, z 8 1 4
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
888
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY
Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
13 P112=a General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos b=a,90<<135
Pmmm
1
2
a b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x,2x y, z 8 1 2
2 cos a=b,90<<135
Cmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x y, y, z 8 1 2
a b
2
p
, 135
P4=mmm
1
2
b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x,2x y, z;
x y, y, z 8 1 4
13 P112=n General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a<b, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos a=b,90<<180
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2y, y, z 8 1 2
a b,90<<180
Cmmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
a b, 90
P4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; y, x, z 8 1 4
13 P112=b General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos a=b,90<<135
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2y, y, z 8 1 2
2 cos b=a,90<<135
Cmmm a
1
2
b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, x y, z 8 1 2
b a
2
p
, 135
P4=mmm
1
2
a b,
1
2
a,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2y, y, z; x, x y, z 8 1 4
14 P12
1
=c1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos a=c,90<<135
Pmmm
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2z, y, z 8 1 2
2 cos c=a,90<<135
Bmmm a
1
2
c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, x z 8 1 2
c a
2
p
, 135
P4=mmm
1
2
a,
1
2
a c,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, x z;
x 2z, y, z 8 1 4
14 P12
1
=n1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a>c, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos c=a,90<<180
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y,2x z 8 1 2
a c,90<<180
Bmmm
1
2
a c,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
z, y, x 8 1 2
a c, 90
P4=mmm
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; z, y, x 8 1 4
14 P12
1
=a1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos c=a,90<<135
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y,2x z 8 1 2
2 cos a=c,90<<135
Bmmm
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x z, y, z 8 1 2
a c
2
p
, 135
P4=mmm
1
2
a c,
1
2
c,
1
2
b
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y,2x z; x z, y, z 8 1 4
14 P112
1
=a General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos b=a,90<<135
Pmmm
1
2
a b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x,2x y, z 8 1 2
2 cos a=b,90<<135
Cmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x y, y, z 8 1 2
a b
2
p
, 135
P4=mmm
1
2
b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x,2x y, z;
x y, y, z 8 1 4
14 P112
1
=n General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
a<b, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos a=b,90<<180
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2y, y, z 8 1 2
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
889
15.2. EUCLIDEAN AND AFFINE NORMALIZERS

Space group G Euclidean normalizer N
E
G Additional generators of N
E
G
Index of
G in N
E
G
No.
Hermann–
Mauguin
symbol Cell metric Symbol Basis vectors Translations
Inversion
through a
centre at Further generators
a b,90<<180
Cmmm
1
2
a b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
y, x, z 8 1 2
a b, 90
P4=mmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z; y, x, z 8 1 4
14 P112
1
=b General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
8 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, y, z 8 1 2
cos a=b,90<<135
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2y, y, z 8 1 2
2 cos b=a,90<<135
Cmmm a
1
2
b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x, x y, z 8 1 2
b a
2
p
, 135
P4=mmm
1
2
a b,
1
2
a,
1
2
c
1
2
,0,0;0,
1
2
,0;0,0,
1
2
x 2y, y, z; x, x y, z 8 1 4
15 C12=c1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
x, y, z 4 1 2
cos c=a,90<<135
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,0,
1
2
x, y,2x z 4 1 2
2 cos a=c,90<<135
Bbmb n2=mn
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,0,
1
2
x z
1
4
, y
1
4
, z 4 1 2
a c
2
p
, 135
P4
2
=mmc
2=m2=mn
1
2
a c,
1
2
c,
1
2
b
1
2
,0,0;0,0,
1
2
x, y,2x z;
x z
1
4
, y
1
4
, z
4 1 4
15 A12=n1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
cos a=c,90<<135
Pmmm
1
2
a,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0
x 2z, y, z 4 1 2
2 cos c=a,90<<135
Bbmb n2=mn a
1
2
c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x, y
1
4
, x z
1
4
4 1 2
c a
2
p
, 135
P4
2
=mmc
2=m2=mn
1
2
a,
1
2
a c,
1
2
b
1
2
,0,0;0,
1
2
,0
x 2z, y, z;
x, y
1
4
, x z
1
4
4 1 4
15 I12=a1 General P12=m1
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a>c, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
cos c=a,90<<180
Pmmm
1
2
a c,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x, y ,2x z 4 1 2
a c,90<<180
Bbmb n2=mn
1
2
a c,
1
2
b,
1
2
a c
1
2
,0,0;0,
1
2
,0 z
1
4
, y
1
4
, x
1
4
4 1 2
a c, 90
P4
2
=mmc
2=m2=mn
1
2
c,
1
2
a,
1
2
b
1
2
,0,0;0,
1
2
,0
x, y, z; z
1
4
, y
1
4
, x
1
4
4 1 4
15 A112=a General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
cos a=b,90<<135
Pmmm
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0
x 2y, y, z 4 1 2
2 cos b=a,90<<135
Cccm nn2=m a
1
2
b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x, x y
1
4
, z
1
4
4 1 2
b a
2
p
, 135
P4
2
=mmc
2=m2=mn
1
2
a b,
1
2
a,
1
2
c
1
2
,0,0;0,
1
2
,0
x 2y, y, z; x, x y
1
4
,
z
1
4
4 1 4
15 B112=n General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x, y, z 4 1 2
cos b=a,90<<135
Pmmm
1
2
a b,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 x,2x y, z 4 1 2
2 cos a=b,90<<135
Cccm nn2=m
1
2
a,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0
x y
1
4
, y, z
1
4
4 1 2
a b
2
p
, 135
P4
2
=mmc
2=m2=mn
1
2
b,
1
2
a b,
1
2
c
1
2
,0,0;0,
1
2
,0 x,2x y, z;
x y
1
4
, y, z
1
4
4 1 4
15 I112=b General P112=m
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0 4 1 1
a<b, 90
Pmmm
1
2
a,
1
2
b,
1
2
c
1
2
,0,0;0,
1
2
,0
x, y, z 4 1 2
Table 15.2.1.3. Euclidean normalizers of the monoclinic and orthorhombic space groups (cont.)
890
15. NORMALIZERS OF SPACE GROUPS AND THEIR USE IN CRYSTALLOGRAPHY
