Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry

Подождите немного. Документ загружается.

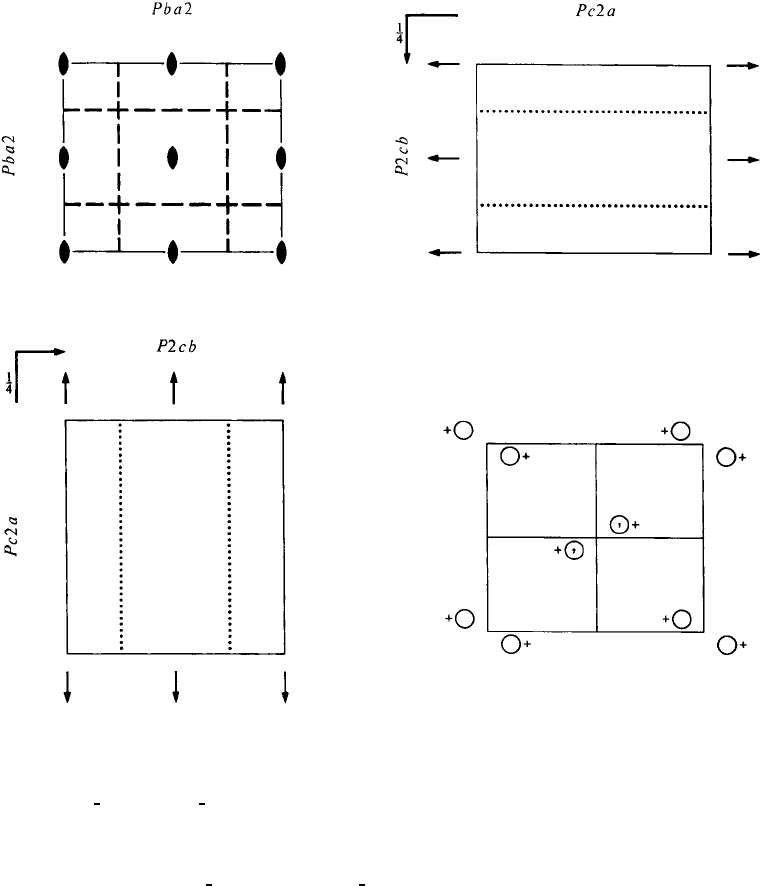
Pba2 C

mm2 Orthorhombic

No. 32 Pba2

Patterson symmetry Pmmm

Origin on 112

Asymmetric unit 0 ≤ x ≤

;0≤ y ≤

;0≤ z ≤ 1

Symmetry operations

(1) 1 (2) 2 0,0,z (3) ax,

,z (4) b

,y,z

232

International Tables for Crystallography (2006). Vol. A, Space group 32, pp. 232–233.

CONTINUED No. 32 Pba2

Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3)

Positions

Multiplicity,

Wyckoff letter,

Site symmetry

Coordinates Reﬂection conditions

General:

4 c 1(1)x,y,z (2) ¯x, ¯y,z (3) x +

, ¯y +

,z (4) ¯x+

,y +

,z 0kl : k = 2n

h0l : h = 2n

h00 : h = 2n

0k0: k = 2n

Special: as above, plus

2 b ..20,

,0, zhkl: h + k = 2n

2 a ..20,0,z

,zhkl: h + k = 2n

Symmetry of special projections

Along [001] p2gg



= ab



= b

Origin at 0,0,z

Along [100] p1m1



= c

Origin at x,0,0

Along [010] p11m



= cb



Origin at 0,y, 0

Maximal non-isomorphic subgroups

[2] P1a1(Pc,7) 1; 3

[2] Pb11(Pc,7) 1; 4

[2] P112 (P2, 3) 1; 2

IIa none

IIb [2] Pnn2(c



= 2c) (34); [2] Pna2



= 2c) (33); [2] Pbn2



= 2c)(Pna2

, 33)

Maximal isomorphic subgroups of lowest index

IIc

[2] Pba2(c



= 2c) (32); [3] Pba2(a



= 3a or b



= 3b) (32)

Minimal non-isomorphic supergroups

[2] Pban(50); [2] Pcca (54); [2] Pbam(55); [2] P4bm(100); [2] P4

bc(106); [2] P

4b2 (117)

II [2] Cmm2 (35); [2] Aea2 (41); [2] Bbe2(Aea2, 41); [2] Iba2 (45); [2] Pbm2(a



a)(Pma2, 28); [2] Pma2(b



b) (28)

233

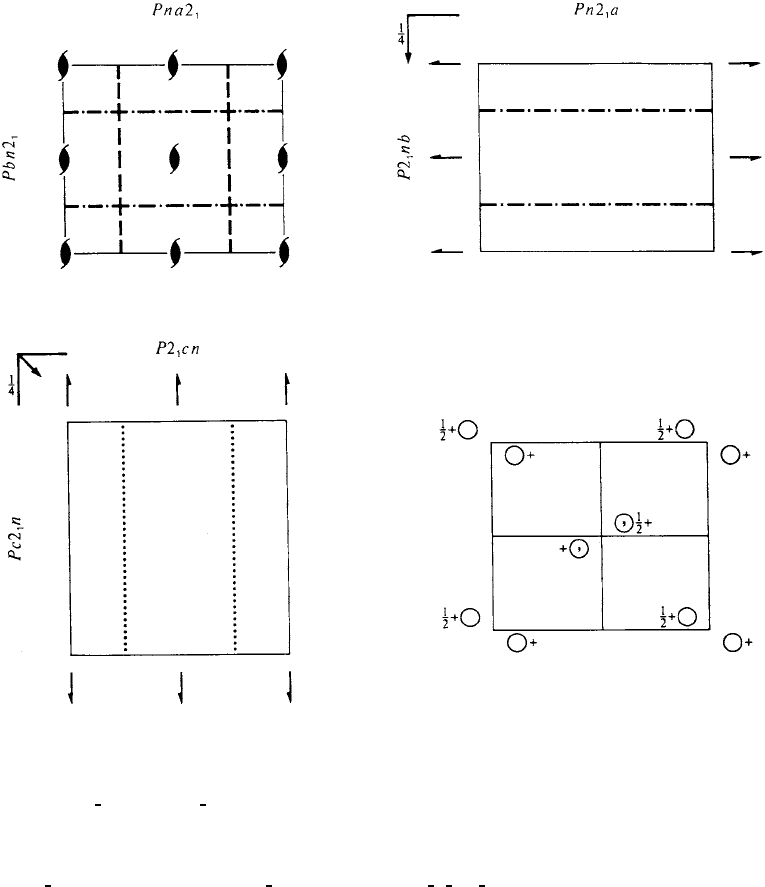
Pna2

mm2 Orthorhombic

No. 33 Pna2

Patterson symmetry Pmmm

Origin on 112

Asymmetric unit 0 ≤ x ≤

;0≤ y ≤

;0≤ z ≤ 1

Symmetry operations

(1) 1 (2) 2(0, 0,

) 0,0,z (3) ax,

,z (4) n(0,

)

,y,z

234

International Tables for Crystallography (2006). Vol. A, Space group 33, pp. 234–235.

CONTINUED No. 33 Pna2

Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3)

Positions

Multiplicity,

Wyckoff letter,

Site symmetry

Coordinates Reﬂection conditions

General:

4 a 1(1)x, y,z (2) ¯x, ¯y,z +

(3) x +

, ¯y +

,z (4) ¯x +

,y +

,z +

0kl : k + l = 2 n

h0l : h = 2n

h00 : h = 2n

0k0: k = 2n

00l : l = 2n

Symmetry of special projections

Along [001] p2gg



= ab



= b

Origin at 0,0,z

Along [100] c1m1



= bb



= c

Origin at x,

Along [010] p11g



= cb



Origin at 0, y,0

Maximal non-isomorphic subgroups

[2] P1a1(Pc,7) 1; 3

[2] Pn11(Pc,7) 1; 4

[2] P112

(P2

,4) 1; 2

IIa none

IIb none

Maximal isomorphic subgroups of lowest index

IIc

[3] Pna2



= 3a) (33); [3] Pna2



= 3b) (33); [3] Pna2



= 3c) (33)

Minimal non-isomorphic supergroups

[2] Pnna(52); [2] Pccn (56); [2] Pbcn (60); [2] Pnma (62)

II [2] Ccm2

(Cmc2

, 36); [2] Ama2 (40); [2] Bbe2(Aea2, 41); [2] Ima2 (46); [2] Pca2



b) (29);

[2] Pnm2



a)(Pmn2

, 31); [2] Pba2(c



c) (32)

235

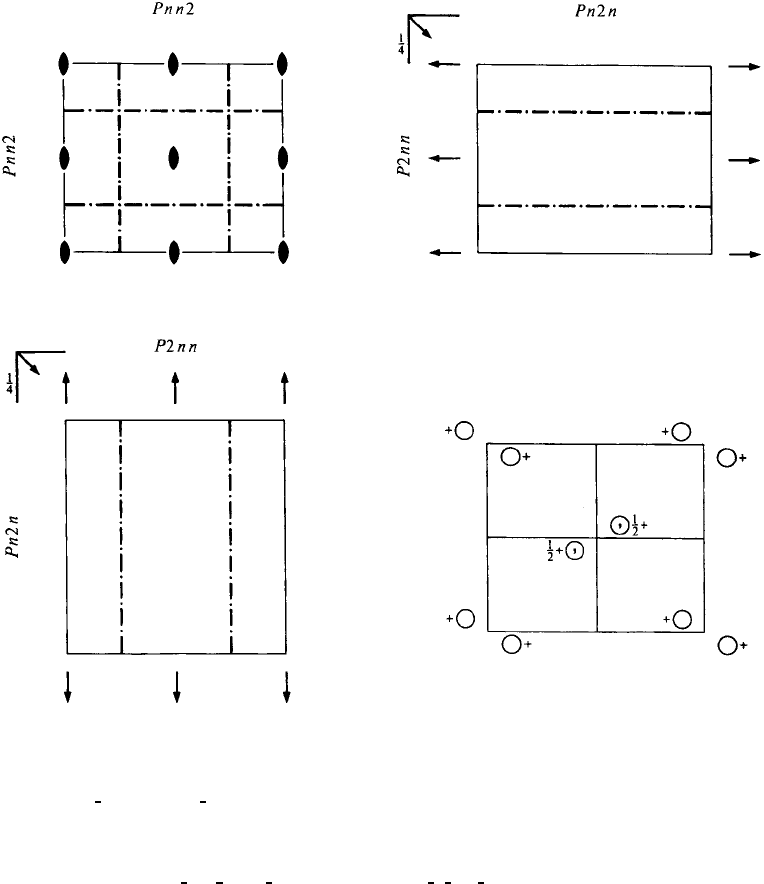
Pnn2 C

mm2 Orthorhombic

No. 34 Pnn2

Patterson symmetry Pmmm

Origin on 112

Asymmetric unit 0 ≤ x ≤

;0≤ y ≤

;0≤ z ≤ 1

Symmetry operations

(1) 1 (2) 2 0,0,z (3) n(

,0,

) x,

,z (4) n(0,

)

,y,z

236

International Tables for Crystallography (2006). Vol. A, Space group 34, pp. 236–237.

CONTINUED No. 34 Pnn2

Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3)

Positions

Multiplicity,

Wyckoff letter,

Site symmetry

Coordinates Reﬂection conditions

General:

4 c 1(1)x,y,z (2) ¯x, ¯y,z (3) x +

, ¯y +

,z +

(4) ¯x+

,y +

,z +

0kl : k + l = 2 n

h0l : h + l = 2n

h00 : h = 2n

0k0: k = 2n

00l : l = 2n

Special: as above, plus

2 b ..20,

,0, z +

hkl : h + k + l = 2n

2 a ..20,0,z

,z +

hkl : h + k + l = 2n

Symmetry of special projections

Along [001] p2gg



= ab



= b

Origin at 0,0,z

Along [100] c1m1



= bb



= c

Origin at x, 0,0

Along [010] c11m



= cb



= a

Origin at 0, y,0

Maximal non-isomorphic subgroups

[2] P1n1(Pc,7) 1; 3

[2] Pn11(Pc,7) 1; 4

[2] P112 (P2, 3) 1; 2

IIa none

IIb [2] Fdd2(a



= 2a,b



= 2b,c



= 2c) (43)

Maximal isomorphic subgroups of lowest index

IIc

[3] Pnn2(a



= 3a or b



= 3b) (34); [3] Pnn2(c



= 3c) (34)

Minimal non-isomorphic supergroups

[2] Pnnn(48); [2] Pnna (52); [2] Pnnm(58); [2] P4

nm(102); [2] P4nc (104); [2] P

4n2 (118)

II [2] Ccc2 (37); [2] Ama2 (40); [2] Bbm2(Ama2, 40); [2] Imm2 (44); [2] Pnc2(a



a) (30); [2] Pcn2(b



b)(Pnc2, 30);

[2] Pba2(c



c) (32)

237

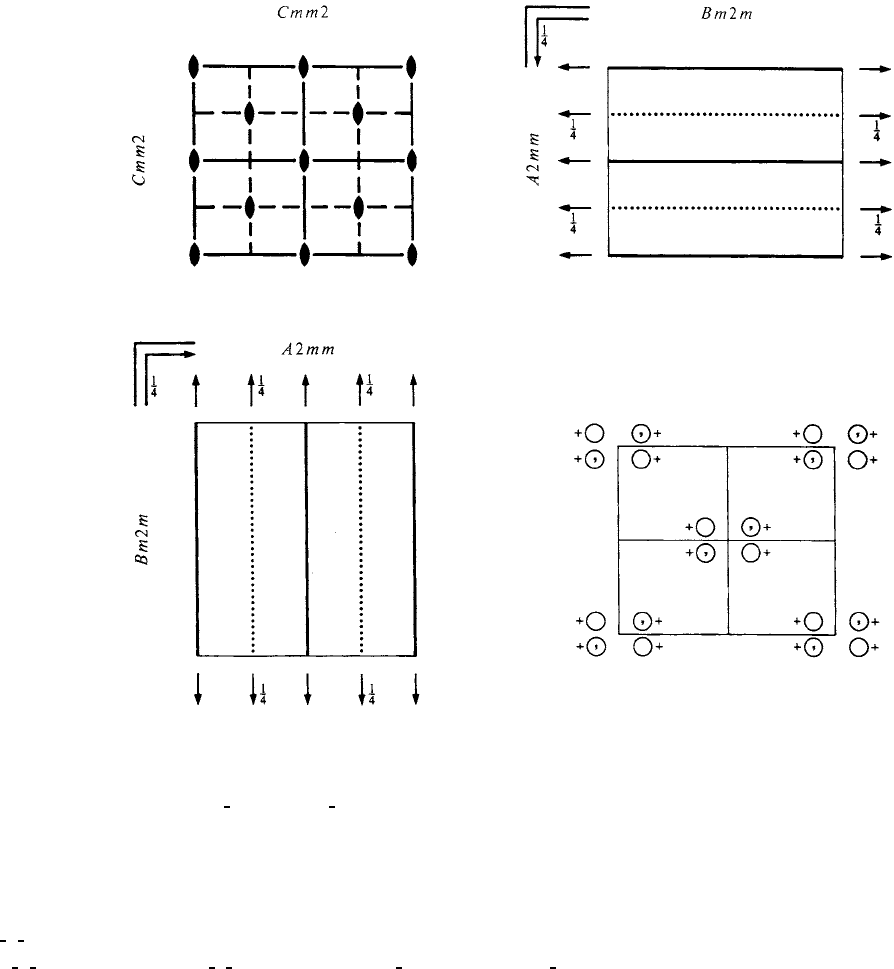
Cmm2 C

mm2 Orthorhombic

No. 35 Cmm2

Patterson symmetry Cmmm

Origin on mm2

Asymmetric unit 0 ≤ x ≤

;0≤ y ≤

;0≤ z ≤ 1

Symmetry operations

For (0,0,0)+ set

(1) 1 (2) 2 0, 0,z (3) mx,0, z (4) m 0,y,z

For (

,0)+ set

(1) t(

,0) (2) 2

,z (3) ax,

,z (4) b

,y,z

238

International Tables for Crystallography (2006). Vol. A, Space group 35, pp. 238–239.

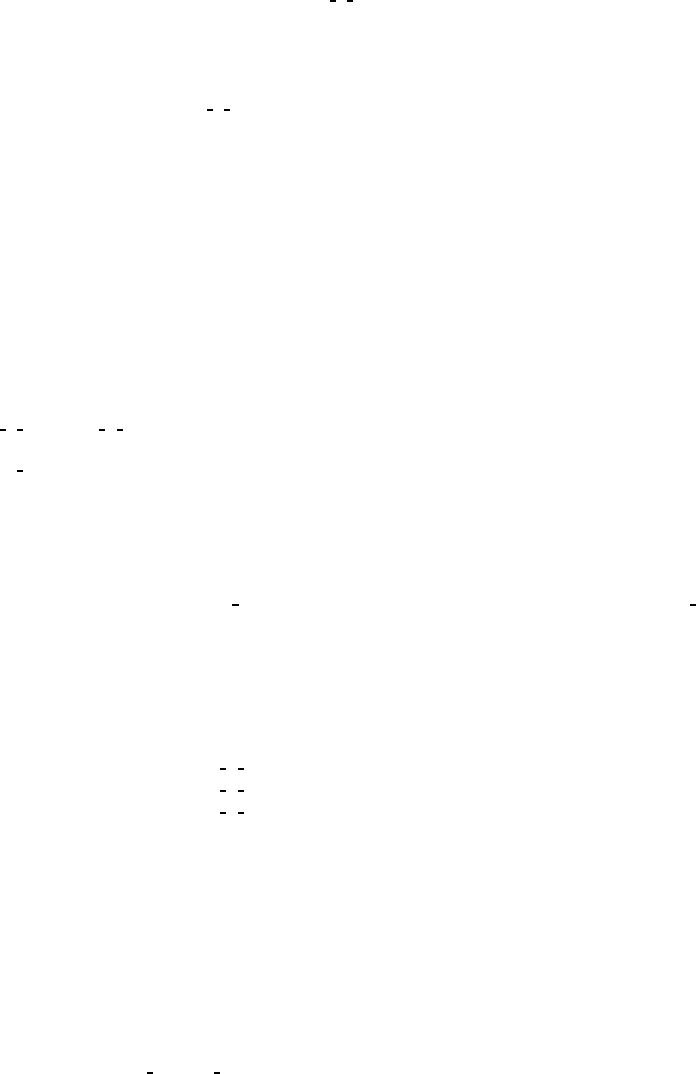
CONTINUED No. 35 Cmm2

Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(

,0); (2); (3)

Positions

Multiplicity,

Wyckoff letter,

Site symmetry

Coordinates

(0,0, 0)+ (

,0)+

Reﬂection conditions

General:

8 f 1(1)x,y,z (2) ¯x, ¯y,z (3) x, ¯y,z (4) ¯x,y,zhkl: h + k = 2n

0kl : k = 2n

h0l : h = 2n

hk0: h + k = 2n

h00 : h = 2n

0k0: k = 2n

Special: as above, plus

4 em.. 0,y,z 0, ¯y,z no extra conditions

4 d . m . x, 0

,z ¯x,0,z no extra conditions

4 c ..2

,zhkl: h = 2n

2 bmm20,

,z no extra conditions

2 amm20, 0,z no extra conditions

Symmetry of special projections

Along [001] c2mm



= ab



= b

Origin at 0,0,z

Along [100] p1m1



= c

Origin at x,0,0

Along [010] p11m



= cb



Origin at 0, y,0

Maximal non-isomorphic subgroups

[2] C 1m1(Cm,8) (1; 3)+

[2] Cm11(Cm,8) (1; 4)+

[2] C 112(P2, 3) (1; 2)+

IIa [2] Pba2 (32) 1; 2; (3; 4)+(

,0)

[2] Pbm2(Pma2, 28) 1; 3; (2; 4)+(

,0)

[2] Pma2 (28) 1; 4; (2; 3)+(

,0)

[2] Pmm2 (25) 1; 2; 3; 4

IIb [2] Ima2(c



= 2c) (46); [2] Ibm2(c



= 2c)(Ima2, 46); [2] Iba2(c



= 2c) (45); [2] Imm2(c



= 2c) (44); [2] Ccc2(c



= 2c) (37);

[2] Cmc2



= 2c) (36); [2] Ccm2



= 2c)(Cmc2

, 36)

Maximal isomorphic subgroups of lowest index

IIc

[2] Cmm2(c



= 2c) (35); [3] Cmm2(a



= 3a or b



= 3b) (35)

Minimal non-isomorphic supergroups

[2] Cmmm (65); [2] Cmme (67); [2] P4mm (99); [2] P4bm (100); [2] P4

cm(101); [2] P4

nm(102); [2] P

42m (111);

[2] P

m (113); [3] P6mm(183)

II [2] Fmm2 (42); [2] Pmm2(a



a,b



b) (25)

239

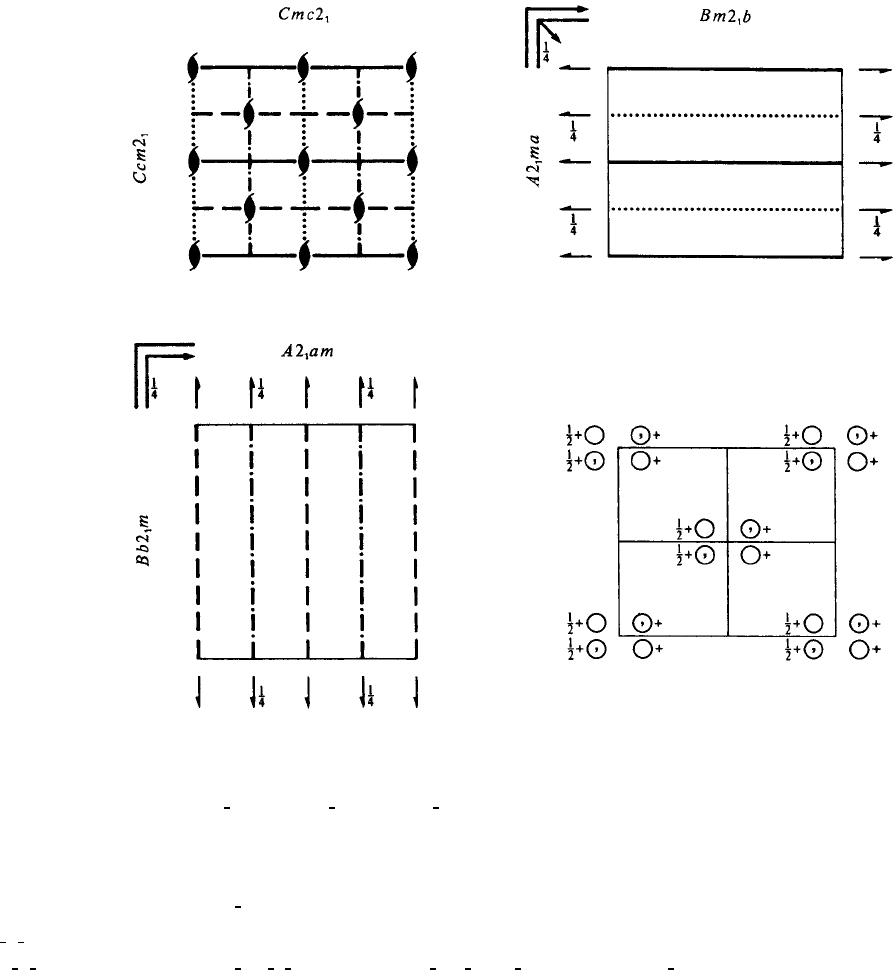
Cmc2

mm2 Orthorhombic

No. 36 Cmc2

Patterson symmetry Cmmm

Origin on mc2

Asymmetric unit 0 ≤ x ≤

;0≤ y ≤

;0≤ z ≤

Symmetry operations

For (0,0,0)+ set

(1) 1 (2) 2(0,0,

) 0,0,z (3) cx,0,z (4) m 0,y,z

For (

,0)+ set

(1) t(

,0) (2) 2(0,0,

)

,z (3) n(

,0,

) x,

,z (4) b

,y,z

240

International Tables for Crystallography (2006). Vol. A, Space group 36, pp. 240–241.

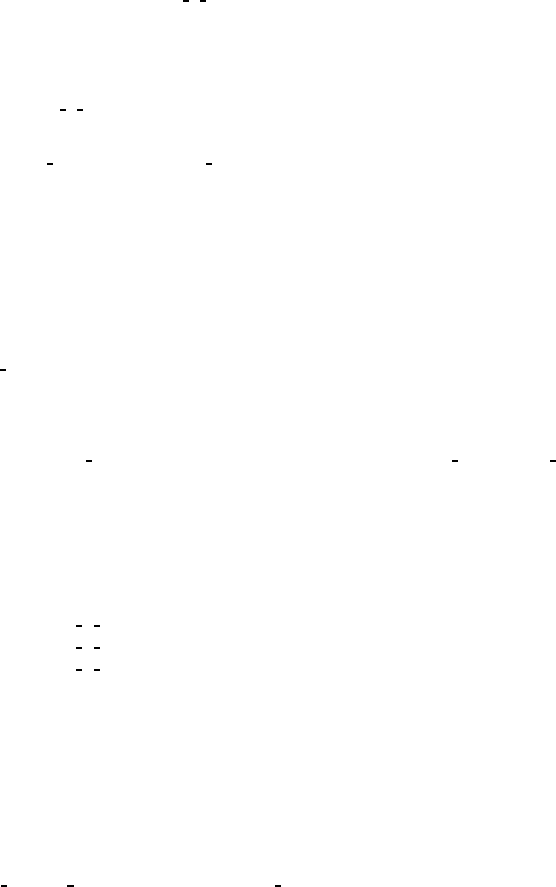
CONTINUED No. 36 Cmc2

Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(

,0); (2); (3)

Positions

Multiplicity,

Wyckoff letter,

Site symmetry

Coordinates

(0,0, 0)+ (

,0)+

Reﬂection conditions

General:

8 b 1(1)x, y,z (2) ¯x, ¯y,z +

(3) x, ¯y, z +

(4) ¯x,y,zhkl: h + k = 2n

0kl : k = 2n

h0l : h, l = 2n

hk0: h + k = 2n

h00 : h = 2n

0k0: k = 2n

00l : l = 2n

Special: no extra conditions

4 am.. 0, y,z 0, ¯y,z +

Symmetry of special projections

Along [001] c2mm



= ab



= b

Origin at 0,0,z

Along [100] p1g1



= c

Origin at x,0,0

Along [010] p11m



Origin at 0,y, 0

Maximal non-isomorphic subgroups

[2] C 1c1(Cc,9) (1; 3)+

[2] Cm11(Cm,8) (1; 4)+

[2] C 112

(P2

,4) (1; 2)+

IIa [2] Pbn2

(Pna2

, 33) 1; 2; (3; 4)+(

,0)

[2] Pmn2

(31) 1; 4; (2; 3)+(

,0)

[2] Pbc2

(Pca2

, 29) 1; 3; (2; 4)+(

,0)

[2] Pmc2

(26) 1; 2; 3; 4

IIb none

Maximal isomorphic subgroups of lowest index

IIc

[3] Cmc2



= 3a) (36); [3] Cmc2



= 3b) (36); [3] Cmc2



= 3c) (36)

Minimal non-isomorphic supergroups

[2] Cmcm(63); [2]Cmce(64); [3] P6

cm(185); [3] P6

mc(186)

II [2] Fmm2 (42); [2] Pmc2



a,b



b) (26); [2] Cmm2(c



c) (35)

241