Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry
Подождите немного. Документ загружается.

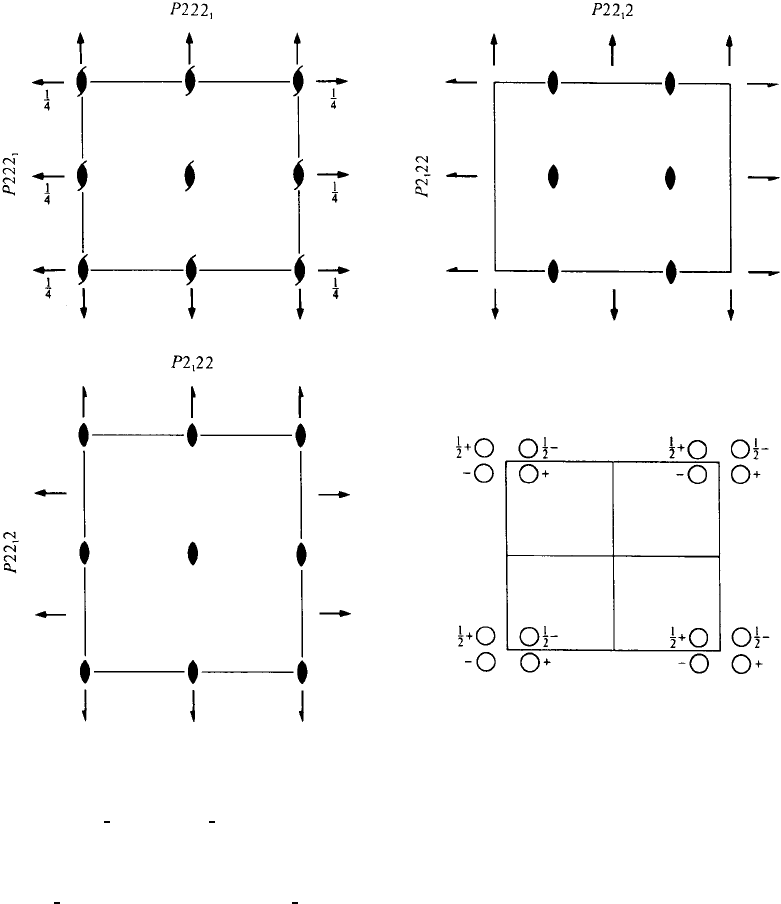
P222
1
D
2
2
222 Orthorhombic
No. 17 P222
1
Patterson symmetry Pmmm
Origin at 212
1
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤ 1
Symmetry operations
(1) 1 (2) 2(0, 0,
1
2
) 0,0,z (3) 2 0,y,
1
4
(4) 2 x , 0,0
202
International Tables for Crystallography (2006). Vol. A, Space group 17, pp. 202–203.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 17 P222
1
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
4 e 1(1)x,y,z (2) ¯x, ¯y,z +
1
2
(3) ¯x,y, ¯z +
1
2
(4) x, ¯y, ¯z 00l : l = 2n
Special: as above, plus
2 d . 2 .
1
2
,y,
1
4
1
2
, ¯y,
3
4
h0l : l = 2n
2 c . 2 . 0,y,
1
4
0, ¯y,
3
4
h0l : l = 2n
2 b 2 .. x,
1
2
,0¯x,
1
2
,
1
2
0kl : l = 2n
2 a 2 .. x, 0,0¯x,0,
1
2
0kl : l = 2n
Symmetry of special projections
Along [001] p2mm
a
= ab
= b
Origin at 0,0,z
Along [100] p2gm
a
= bb
= c
Origin at x,0,0
Along [010] p2mg
a
= cb
= a
Origin at 0,y,
1
4
Maximal non-isomorphic subgroups
I
[2] P112
1
(P2
1
,4) 1; 2
[2] P121 (P2, 3) 1; 3
[2] P211 (P2, 3) 1; 4
IIa none
IIb [2] P2
1
22
1
(a
= 2a)(P2
1
2
1
2, 18); [2] P22
1
2
1
(b
= 2b)(P2
1
2
1
2, 18); [2]C 222
1
(a
= 2a,b
= 2b) (20)
Maximal isomorphic subgroups of lowest index
IIc
[2] P222
1
(a
= 2a or b
= 2b) (17); [3] P222
1
(c
= 3c) (17)
Minimal non-isomorphic supergroups
I
[2] Pmma (51); [2] Pnna (52); [2] Pmna (53); [2] Pcca (54); [2] P4
1
22 (91); [2] P4
3
22 (95)
II [2] C 222
1
(20); [2] A222 (C222, 21); [2] B222(C222, 21); [2] I 2
1
2
1
2
1
(24); [2] P222(c
=
1
2
c) (16)
203
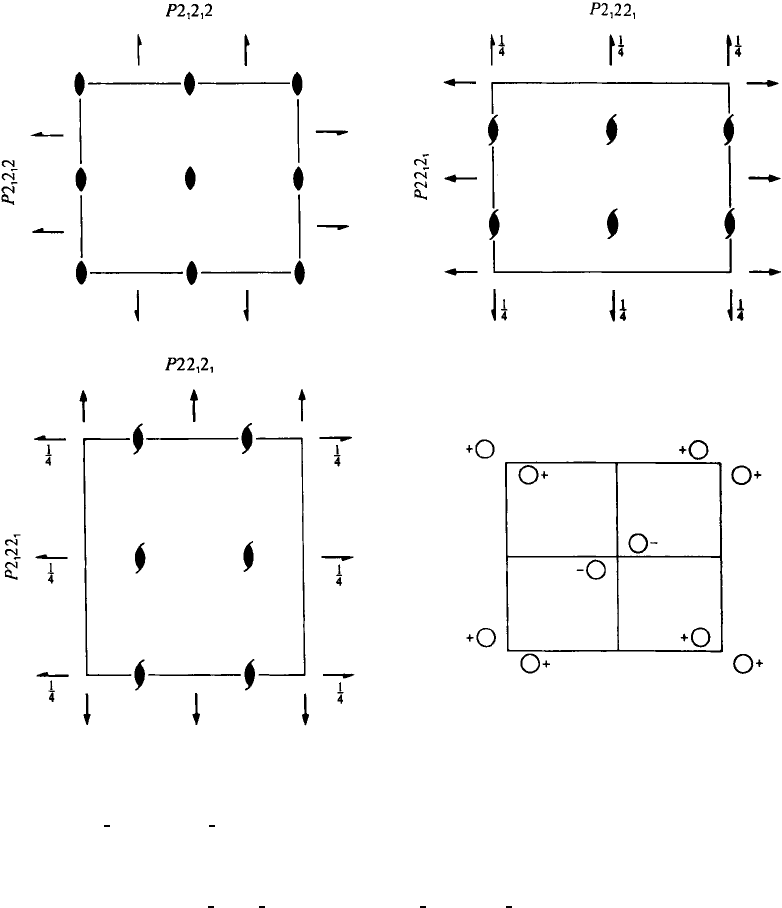
P2
1
2
1
2 D
3
2
222 Orthorhombic
No. 18 P2
1
2
1
2 Patterson symmetry Pmmm
Origin at intersection of 2 with perpendicular plane co ntaining 2
1
axes
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤ 1
Symmetry operations
(1) 1 (2) 2 0,0,z (3) 2(0,
1
2
,0)
1
4
,y,0(4)2(
1
2
,0, 0) x,
1
4
,0
204
International Tables for Crystallography (2006). Vol. A, Space group 18, pp. 204–205.
Copyright © 2006 International Union of Crystallography
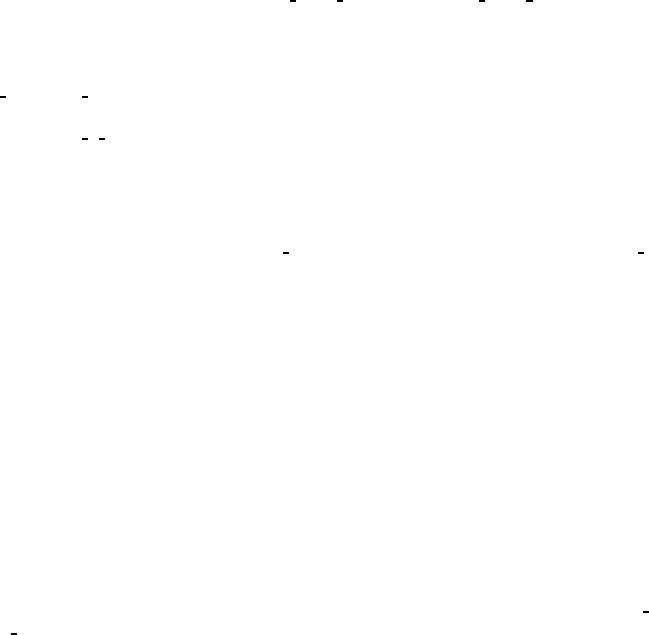
CONTINUED No. 18 P2
1
2
1
2
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
4 c 1(1)x,y,z (2) ¯x, ¯y,z (3) ¯x+
1
2
,y +
1
2
, ¯z (4) x +
1
2
, ¯y +
1
2
, ¯zh00 : h = 2n
0k0: k = 2n
Special: as above, plus
2 b ..20,
1
2
,z
1
2
,0, ¯zhk0: h + k = 2n
2 a ..20,0,z
1
2
,
1
2
, ¯zhk0: h + k = 2n
Symmetry of special projections
Along [001] p2gg
a
= ab
= b
Origin at 0,0,z
Along [100] p2mg
a
= bb
= c
Origin at x,
1
4
,0
Along [010] p2gm
a
= cb
= a
Origin at
1
4
,y,0
Maximal non-isomorphic subgroups
I
[2] P12
1
1(P2
1
,4) 1; 3
[2] P2
1
11(P2
1
,4) 1; 4
[2] P112 (P2, 3) 1; 2
IIa none
IIb [2] P2
1
2
1
2
1
(c
= 2c) (19)
Maximal isomorphic subgroups of lowest index
IIc
[2] P2
1
2
1
2(c
= 2c) (18); [3] P2
1
2
1
2(a
= 3a or b
= 3b) (18)
Minimal non-isomorphic supergroups
I
[2] Pbam(55); [2] Pccn (56); [2] Pbcm(57); [2] Pnnm(58); [2] Pmmn (59); [2] Pbcn(60); [2] P42
1
2 (90); [2] P4
2
2
1
2 (94);
[2] P
¯
42
1
m (113); [2] P
¯
42
1
c (114)
II [2] A2
1
22(C222
1
, 20); [2] B22
1
2(C 222
1
, 20); [2]C 222 (21); [2] I 222 (23); [2] P22
1
2(a
=
1
2
a)(P222
1
, 17);
[2] P2
1
22(b
=
1
2
b)(P222
1
, 17)
205
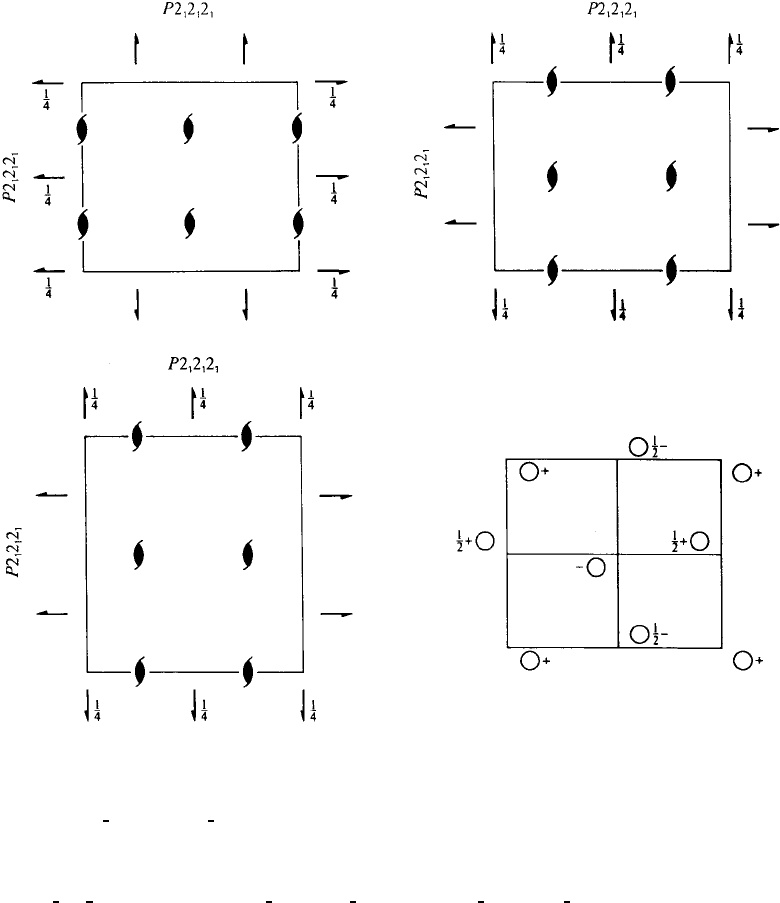
P2
1
2
1
2
1
D
4
2
222 Orthorhombic
No. 19 P2
1
2
1
2
1
Patterson symmetry Pmmm
Origin at midpoint of three non-intersecting pairs of parallel 2
1
axes
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤ 1
Symmetry operations
(1) 1 (2) 2(0, 0,
1
2
)
1
4
,0, z (3) 2(0,
1
2
,0) 0, y,
1
4
(4) 2(
1
2
,0, 0) x,
1
4
,0
206
International Tables for Crystallography (2006). Vol. A, Space group 19, pp. 206–207.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 19 P2
1
2
1
2
1
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
4 a 1(1)x, y,z (2) ¯x +
1
2
, ¯y, z +
1
2
(3) ¯x,y +
1
2
, ¯z +
1
2
(4) x +
1
2
, ¯y +
1
2
, ¯zh00 : h = 2n
0k0: k = 2n
00l : l = 2n
Symmetry of special projections
Along [001] p2gg
a
= ab
= b
Origin at
1
4
,0, z
Along [100] p2gg
a
= bb
= c
Origin at x,
1
4
,0
Along [010] p2gg
a
= cb
= a
Origin at 0,y,
1
4
Maximal non-isomorphic subgroups
I
[2] P112
1
(P2
1
,4) 1; 2
[2] P12
1
1(P2
1
,4) 1; 3
[2] P2
1
11(P2
1
,4) 1; 4
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] P2
1
2
1
2
1
(a
= 3a or b
= 3b or c
= 3c) (19)
Minimal non-isomorphic supergroups
I
[2] Pbca (61); [2] Pnma (62); [2] P4
1
2
1
2 (92); [2] P4
3
2
1
2 (96); [3] P2
1
3 (198)
II [2] A2
1
22(C222
1
, 20); [2] B22
1
2(C 222
1
, 20); [2]C 222
1
(20); [2] I 2
1
2
1
2
1
(24); [2] P22
1
2
1
(a
=
1
2
a)(P2
1
2
1
2, 18);
[2] P2
1
22
1
(b
=
1
2
b)(P2
1
2
1
2, 18); [2] P2
1
2
1
2(c
=
1
2
c) (18)
207
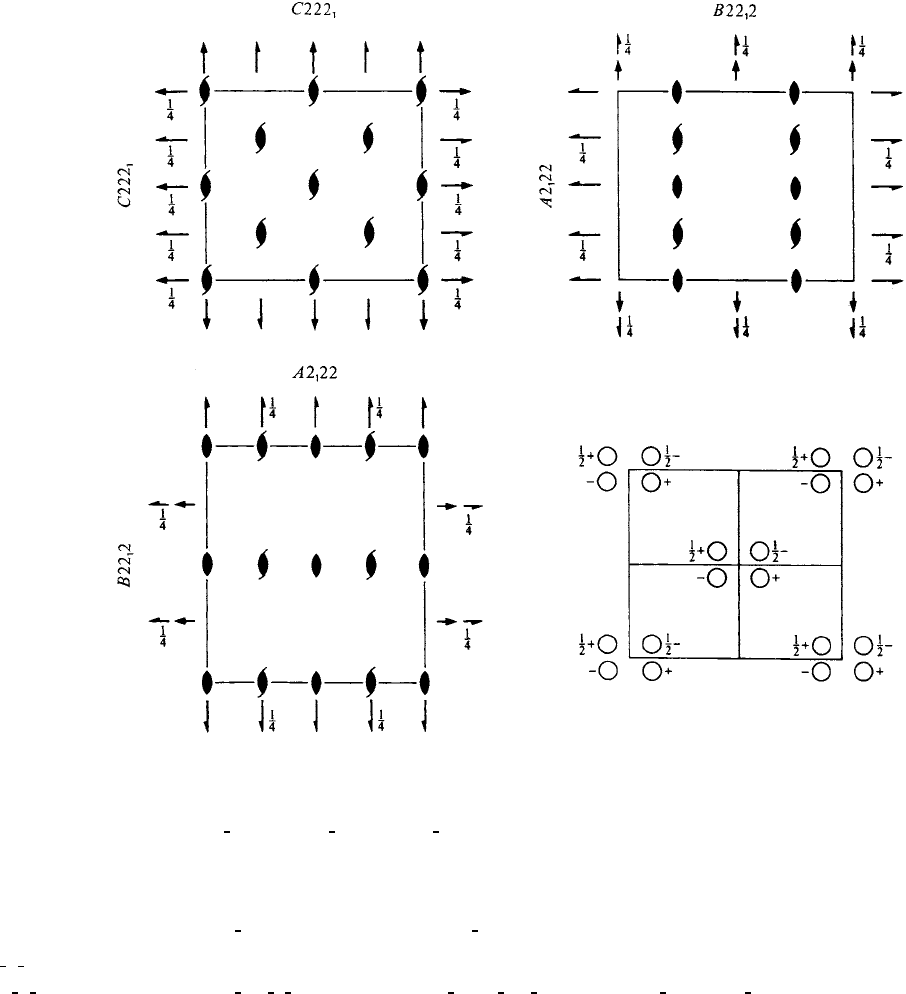
C222
1
D
5
2
222 Orthorhombic
No. 20 C222
1
Patterson symmetry Cmmm
Origin at 212
1
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
2
Symmetry operations
For (0,0,0)+ set
(1) 1 (2) 2(0,0,
1
2
) 0,0,z (3) 2 0,y,
1
4
(4) 2 x,0,0
For (
1
2
,
1
2
,0)+ set
(1) t(
1
2
,
1
2
,0) (2) 2(0,0,
1
2
)
1
4
,
1
4
,z (3) 2(0,
1
2
,0)
1
4
,y,
1
4
(4) 2(
1
2
,0, 0) x,
1
4
,0
208
International Tables for Crystallography (2006). Vol. A, Space group 20, pp. 208–209.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 20 C 222
1
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(
1
2
,
1
2
,0); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates
(0,0, 0)+ (
1
2
,
1
2
,0)+
Reflection conditions
General:
8 c 1(1)x,y,z (2) ¯x, ¯y,z +
1
2
(3) ¯x,y, ¯z +
1
2
(4) x, ¯y, ¯zhkl: h + k = 2n
0kl : k = 2n
h0l : h = 2n
hk0: h + k = 2n
h00 : h = 2n
0k0: k = 2n
00l : l = 2n
Special: as above, plus
4 b . 2 . 0,y,
1
4
0, ¯y,
3
4
h0l : l = 2n
4 a 2 .. x, 0,0¯x,0,
1
2
0kl : l = 2n
Symmetry of special projections
Along [001] c2mm
a
= ab
= b
Origin at 0,0,z
Along [100] p2gm
a
=
1
2
bb
= c
Origin at x,0,0
Along [010] p2mg
a
= cb
=
1
2
a
Origin at 0, y,
1
4
Maximal non-isomorphic subgroups
I
[2] C 121(C2, 5) (1; 3)+
[2] C 211(C2, 5) (1; 4)+
[2] C 112
1
(P2
1
,4) (1; 2)+
IIa [2] P2
1
2
1
2
1
(19) 1; 2; (3; 4 )+(
1
2
,
1
2
,0)
[2] P2
1
22
1
(P2
1
2
1
2, 18) 1; 3; (2; 4)+(
1
2
,
1
2
,0)
[2] P22
1
2
1
(P2
1
2
1
2, 18) 1; 4; (2; 3)+(
1
2
,
1
2
,0)
[2] P222
1
(17) 1; 2; 3; 4
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] C 222
1
(a
= 3a or b
= 3b) (20); [3]C 222
1
(c
= 3c) (20)
Minimal non-isomorphic supergroups
I
[2] Cmcm(63); [2]Cmce(64); [2] P4
1
22 (91); [2] P4
1
2
1
2 (92); [2] P4
3
22 (95); [2] P4
3
2
1
2 (96); [3] P6
1
22 (178);
[3] P6
5
22 (179); [3] P6
3
22 (182)
II [2] F 222 (22); [2] P222
1
(a
=
1
2
a,b
=
1
2
b) (17); [2] C222(c
=
1
2
c) (21)
209
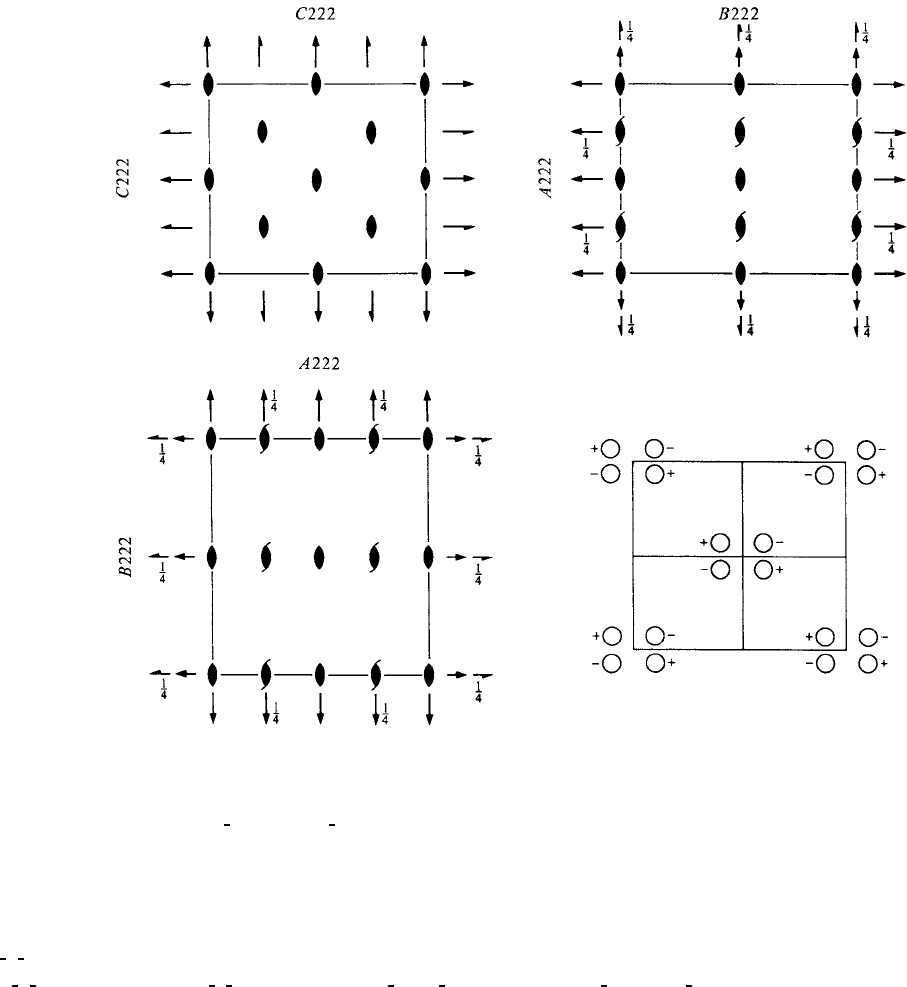
C222 D
6
2
222 Orthorhombic
No. 21 C222
Patterson symmetry Cmmm
Origin at 222
Asymmetric unit 0 ≤ x ≤
1
4
;0≤ y ≤
1
2
;0≤ z ≤ 1
Symmetry operations
For (0,0,0)+ set
(1) 1 (2) 2 0, 0,z (3) 2 0,y,0(4)2x,0,0
For (
1
2
,
1
2
,0)+ set
(1) t(
1
2
,
1
2
,0) (2) 2
1
4
,
1
4
,z (3) 2(0,
1
2
,0)
1
4
,y,0(4)2(
1
2
,0, 0) x,
1
4
,0
210
International Tables for Crystallography (2006). Vol. A, Space group 21, pp. 210–211.
Copyright © 2006 International Union of Crystallography
CONTINUED No. 21 C222
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(
1
2
,
1
2
,0); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates
(0,0, 0)+ (
1
2
,
1
2
,0)+
Reflection conditions
General:
8 l 1(1)x,y,z (2) ¯x, ¯y,z (3) ¯x,y, ¯z (4) x, ¯y, ¯zhkl: h + k = 2n
0kl : k = 2n
h0l : h = 2n
hk0: h + k = 2n
h00 : h = 2n
0k0: k = 2n
Special: as above, plus
4 k ..2
1
4
,
1
4
,z
3
4
,
1
4
, ¯zhk0: h = 2n
4 j ..20,
1
2
,z 0,
1
2
, ¯z no extra conditions
4 i ..20,0, z 0,0, ¯z no extra conditions
4 h . 2 . 0, y,
1
2
0, ¯y,
1
2
no extra conditions
4 g . 2 . 0, y,00, ¯y, 0 no extra conditions
4 f 2 .. x,0,
1
2
¯x,0,
1
2
no extra conditions
4 e 2 .. x,0,0¯x, 0,0 no extra conditions
2 d 222 0,0,
1
2
no extra conditions
2 c 222
1
2
,0,
1
2
no extra conditions
2 b 222 0,
1
2
,0 no extra conditions
2 a 222 0,0,0 no extra conditions
Symmetry of special projections
Along [001] c2mm
a
= ab
= b
Origin at 0,0,z
Along [100] p2mm
a
=
1
2
bb
= c
Origin at x,0,0
Along [010] p2mm
a
= cb
=
1
2
a
Origin at 0,y, 0
Maximal non-isomorphic subgroups
I
[2] C 121(C2, 5) (1; 3)+
[2] C 211(C2, 5) (1; 4)+
[2] C 112(P2, 3) (1; 2)+
IIa [2] P2
1
2
1
2 (18) 1; 2; (3; 4)+(
1
2
,
1
2
,0)
[2] P2
1
22(P222
1
, 17) 1; 3; (2; 4)+(
1
2
,
1
2
,0)
[2] P22
1
2(P222
1
, 17) 1; 4; (2; 3)+(
1
2
,
1
2
,0)
[2] P222 (16) 1; 2; 3; 4
IIb [2] I 2
1
2
1
2
1
(c
= 2c) (24); [2] I 222 (c
= 2c) (23); [2] C222
1
(c
= 2c) (20)
Maximal isomorphic subgroups of lowest index
IIc
[2] C 222(c
= 2c) (21); [3] C222 (a
= 3a or b
= 3b) (21)
Minimal non-isomorphic supergroups
I
[2] Cmmm (65); [2] Cccm (66); [2] Cmme (67); [2] Ccce (68); [2] P422 (89); [2] P42
1
2 (90); [2] P4
2
22 (93); [2] P4
2
2
1
2 (94);
[2] P
¯
4m2 (115); [2] P
¯
4c2 (116); [2] P
¯
4b2 (117); [2] P
¯
4n2 (118); [3] P622 (177); [3] P6
2
22 (180); [3] P6
4
22 (181)
II [2] F 222 (22); [2] P222(a
=
1
2
a,b
=
1
2
b) (16)
211
