Hager G., Wellein G. Introduction to High Performance Computing for Scientists and Engineers

Подождите немного. Документ загружается.

Modern processors 15

1.3 Memory hierarchies

Data can be stored in a computer system in many different ways. As described

above, CPUs have a set of registers, which can be accessed without delay. In ad-

dition there are one or more small but very fast caches holding copies of recently

used data items. Main memory is much slower, but also much larger than cache. Fi-

nally, data can be stored on disk and copied to main memory as needed. This a is a

complex hierarchy, and it is vital to understand how data transfer works between the

different levels in order to identify performance bottlenecks. In the following we will

concentrate on all levels from CPU to main memory (see Figure 1.3).

1.3.1 Cache

Caches are low-capacity, high-speed memories that are commonly integrated on

the CPU die. The need for caches can be easily understood by realizing that data

transfer rates to main memory are painfully slow compared to the CPU’s arithmetic

performance. While peak performance soars at several GFlops/sec per core, memory

bandwidth, i.e., the rate at which data can be transferred from memory to the CPU,

is still stuck at a couple of GBytes/sec, which is entirely insufﬁcient to feed all arith-

metic units and keep them busy continuously (see Chapter 3 for a more thorough

analysis). To make matters worse, in order to transfer a single data item (usually

one or two DP words) from memory, an initial waiting time called latency passes

until data can actually ﬂow. Thus, latency is often deﬁned as the time it takes to

transfer a zero-byte message. Memory latency is usually of the order of several hun-

dred CPU cycles and is composed of different contributions from memory chips, the

chipset and the processor. Although Moore’s Law still guarantees a constant rate of

improvement in chip complexity and (hopefully) performance, advances in memory

performance show up at a much slower rate. The term DRAM gap has been coined

for the increasing “distance” between CPU and memory in terms of latency and

bandwidth [R34, R37].

Caches can alleviate the effects of the DRAM gap in many cases. Usually there

are at least two levels of cache (see Figure 1.3), called L1 and L2, respectively. L1 is

normally split into two parts, one for instructions (“I-cache,” “L1I”) and one for data

(“L1D”). Outer cache levels are normally uniﬁed, storing data as well as instructions.

In general, the “closer”a cache is to the CPU’s registers, i.e., the higher itsbandwidth

and the lower its latency, the smaller it must be to keep administration overhead low.

Whenever the CPU issues a read request (“load”) for transferring a data item to a

it does, this is called a cache hit and the request can be satisﬁed immediately, with

low latency. In case of a cache miss, however, data must be fetched from outer cache

levels or, in the worst case, from main memory. If all cache entries are occupied, a

hardware-implemented algorithm evicts old items from cache and replaces them with

new data. The sequence of events for a cache miss on a write is more involved and

16 Introduction to High Performance Computing for Scientists and Engineers

Figure 1.9: The perfor-

mance gain from access-

ing data from cache ver-

sus the cache reuse ra-

tio, with the speed ad-

vantage of cache ver-

sus main memory being

parametrized by

0.7 0.75 0.8 0.85 0.9 0.95 1

G(τ,β)

τ=5

τ=10

τ=50

will be described later. Instruction caches are usually of minor importance since sci-

entiﬁc codes tend to be largely loop-based; I-cache misses are rare events compared

to D-cache misses.

Caches can only have a positive effect on performance if the data access pattern

of an application shows some locality of reference. More speciﬁcally, data items that

have been loaded into a cache are to be used again “soon enough” to not have been

evicted in the meantime. This is also called temporal locality. Using a simple model,

we will now estimate the performance gain that can be expected from a cache that

is a factor of

faster than memory (this refers to bandwidth as well as latency; a

more reﬁned model is possible but does not lead to additional insight). Let

be the

cache reuse ratio, i.e., the fraction of loads or stores that can be satisﬁed from cache

because there was a recent load or store to the same address. Access time to main

memory (again this includes latency and bandwidth) is denoted by T

. In cache,

access time is reduced to T

= T

. For some ﬁnite

, the average access time will

thus be T

+ (1−

, and we calculate an access performance gain of

) =

+ (1−

)

(1−

)

. (1.4)

As Figure 1.9 shows, a cache can only lead to a signiﬁcant performance advantage if

the reuse ratio is relatively close to one.

Unfortunately, supporting temporal locality is not sufﬁcient. Many applications

show streaming patterns where large amounts of data are loaded into the CPU, mod-

iﬁed, and written back without the potential of reuse “in time.” For a cache that only

supports temporal locality, the reuse ratio

(see above) is zero for streaming. Each

new load is expensive as an item has to be evicted from cache and replaced by the

new one, incurring huge latency. In order to reduce the latency penalty for streaming,

caches feature a peculiar organization into cache lines. All data transfers between

caches and main memory happen on the cache line level (there may be exceptions

from that rule; see the comments on nontemporal stores on page 18 for details). The

Modern processors 17

advantage of cache lines is that the latency penalty of a cache miss occurs only on

the ﬁrst miss on an item belonging to a line. The line is fetched from memory as a

whole; neighboring items can then be loaded from cache with much lower latency,

increasing the cache hit ratio

, not to be confused with the reuse ratio

. So if the

application shows some spatial locality, i.e., if the probability of successive accesses

to neighboring items is high, the latency problem can be signiﬁcantly reduced. The

downside of cache lines is that erratic data access patterns are not supported. On the

contrary, not only does each load incur a miss and subsequent latency penalty, it also

leads to the transfer of a whole cache line, polluting the memory bus with data that

will probably never be used. The effective bandwidth available to the application will

thus be very low. On the whole, however, the advantages of using cache lines pre-

vail, and very few processor manufacturers have provided means of bypassing the

mechanism.

Assuming a streaming application working on DP ﬂoating point data on a CPU

with a cache line length of L

= 16 words, spatial locality ﬁxes the hit ratio at

(16 − 1)/16 = 0.94, a seemingly large value. Still it is clear that performance is

governed by main memory bandwidth and latency — the code is memory-bound. In

order for an application to be truly cache-bound, i.e., decouple from main memory so

that performance is not governed by memory bandwidth or latency any more,

must

be large enough so the time it takes to process in-cache data becomes larger than the

time for reloading it. If and when this happens depends of course on the details of

the operations performed.

By now we can qualitatively interpret the performance data for cache-based ar-

chitectures on the vector triad in Figure 1.4. At very small loop lengths, the processor

pipeline is too long to be efﬁcient. With growing N this effect becomes negligible,

and as long as all four arrays ﬁt into the innermost cache, performance saturates at

a high value that is set by the L1 cache bandwidth and the ability of the CPU to is-

sue load and store instructions. Increasing N a little more gives rise to a sharp drop

in performance because the innermost cache is not large enough to hold all data.

Second-level cache has usually larger latency but similar bandwidth to L1 so that

the penalty is larger than expected. However, streaming data from L2 has the disad-

vantage that L1 now has to provide data for registers as well as continuously reload

and evict cache lines from/to L2, which puts a strain on the L1 cache’s bandwidth

limits. Since the ability of caches to deliver data to higher and lower hierarchy levels

concurrently is highly architecture-dependent, performance is usually hard to predict

on all but the innermost cache level and main memory. For each cache level another

performance drop is observed with rising N, until ﬁnally even the large outer cache is

too small and all data has to be streamed from main memory. The size of the different

caches is directly related to the locations of the bandwidth breakdowns. Section 3.1

will describe how to predict performance for simple loops from basic parameters like

cache or memory bandwidths and the data demands of the application.

Storing data is a little more involved than reading. In presence of caches, if data

to be written out already resides in cache, a write hit occurs. There are several pos-

sibilities for handling this case, but usually outermost caches work with a write-back

strategy: The cache line is modiﬁed in cache and written to memory as a whole when

18 Introduction to High Performance Computing for Scientists and Engineers

evicted. On a write miss, however, cache-memory consistency dictates that the cache

line in question must ﬁrst be transferred from memory to cache before an entry can

be modiﬁed. This is called write allocate, and leads to the situation that a data write

stream from CPU to memory uses the bus twice: once for all the cache line alloca-

tions and once for evicting modiﬁed lines (the data transfer requirement for the triad

benchmark code is increased by 25% due to write allocates). Consequently, stream-

ing applications do not usually proﬁtfrom write-back caches andthere is often a wish

for avoiding write-allocate transactions. Some architectures provide this option, and

there are generally two different strategies:

• Nontemporal stores. These are special store instructions that bypass all cache

levels and write directly to memory. Cache does not get “polluted” by store

streams that do not exhibit temporal locality anyway. In order to prevent ex-

cessive latencies, there is usually a small write combine buffer, which bundles

a number of successive nontemporal stores [V104].

• Cache line zero. Special instructions “zero out” a cache line and mark it as

modiﬁed without a prior read. The data is written to memory when evicted.

In comparison to nontemporal stores, this technique uses up cache space for

the store stream. On the other hand it does not slow down store operations in

cache-bound situations. Cache line zero must be used with extreme care: All

elements of a cache line are evicted to memory, even if only a part of them

were actually modiﬁed.

Both can be applied by the compiler and hinted at by the programmer by means

of directives. In very simple cases compilers are able to apply those instructions

automatically in their optimization stages, but one must take care to not slow down

a cache-bound code by using nontemporal stores, rendering it effectively memory-

bound.

Note that the need for write allocates arises because caches and memory gener-

ally communicate in units of cache lines; it is a common misconception that write

allocates are only required to maintain consistency between caches of multiple pro-

cessor cores.

1.3.2 Cache mapping

So far we have implicitly assumed that there is no restriction on which cache line

can be associated with which memory locations. A cache design that follows this

rule is called fully associative. Unfortunately it is quite hard to build large, fast, and

fully associative caches because of large bookkeeping overhead: For each cache line

the cache logic must store its location in the CPU’s address space, and each mem-

ory access must be checked against the list of all those addresses. Furthermore, the

decision which cache line to replace next if the cache is full is made by some algo-

rithm implemented in hardware. Often there is a least recently used (LRU) strategy

that makes sure only the “oldest” items are evicted, but alternatives like NRU (not

recently used ) or random replacement are possible.

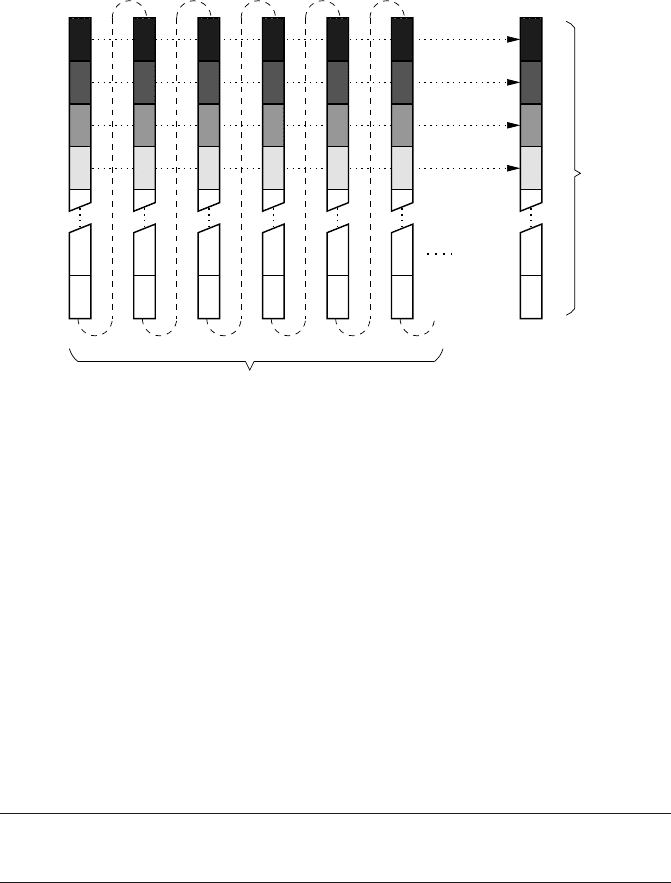
Modern processors 19

Cache

Memory

Figure 1.10: In a direct-mapped cache, memory locations which lie a multiple of the cache

size apart are mapped to the same cache line (shaded boxes).

The most straightforward simpliﬁcation of this expensive scheme consists in a

direct-mapped cache, which maps the full cache size repeatedly into memory (see

Figure 1.10). Memory locations that lie a multiple of the cache size apart are always

mapped to the same cache line, and the cache line that corresponds to some address

can be obtained very quickly by masking out the most signiﬁcant bits. Moreover, an

algorithm to select which cache line to evict is pointless. No hardware and no clock

cycles need to be spent for it.

The downside of a direct-mapped cache is that itis disposed toward cache thrash-

ing, which means that cache lines are loaded into and evicted from the cache in rapid

succession. This happens when an application uses many memory locations that get

mapped to the same cache line. A simple example would be a “strided” vector triad

code for DP data, which is obtained by modifying the inner loop as follows:

1 do i=1,N,CACHE_SIZE_IN_BYTES/8

2 A(i) = B(i) + C(i)

D(i)

3 enddo

By using the cache size in units of DP words as a stride, successive loop iterations

hit the same cache line so that every memory access generates a cache miss, even

though a whole line is loaded every time. In principle there is plenty of room left in

the cache, so this kind of situation is called a conﬂict miss. If the stride were equal to

the line length there would still be some (albeit small) N for which the cache reuse is

100%. Here, the reuse fraction is exactly zero no matter how small N may be.

To keep administrative overhead low and still reduce the danger of conﬂict misses

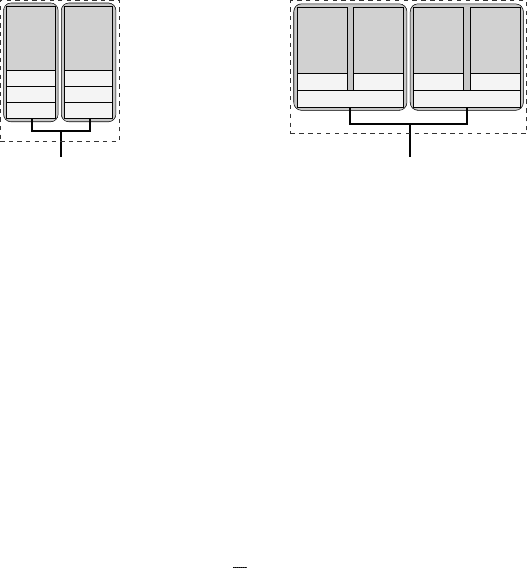
and cache thrashing, a set-associative cache is divided into m direct-mapped caches

20 Introduction to High Performance Computing for Scientists and Engineers

Cache

Memory

Way 1

Way 2

Figure 1.11: In an m-way set-associative cache, memory locations which are located a mul-

tiple of

th of the cache size apart can be mapped to either of m cache lines (here shown for

m = 2).

equal in size, so-called ways. The number of ways m is the number of different cache

lines a memory address can be mapped to (see Figure 1.11 for an example of a

two-way set-associative cache). On each memory access, the hardware merely has to

determine which way the data resides in or, in the case of a miss, to which of the m

possible cache lines it should be loaded.

For each cache level the tradeoff between low latency and prevention of thrashing

must be considered by processor designers. Innermost (L1) caches tend to be less

set-associative than outer cache levels. Nowadays, set-associativity varies between

two- and 48-way. Still, the effective cache size, i.e., the part of the cache that is

actually useful for exploiting spatial and temporal locality in an application code

could be quite small, depending on the number of data streams, their strides and

mutual offsets. See Chapter 3 for examples.

1.3.3 Prefetch

Although exploiting spatial locality by the introduction of cache lines improves

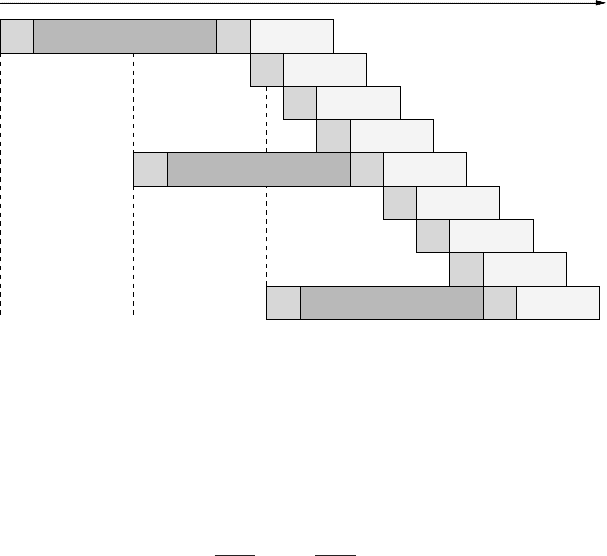
cache efﬁciency a lot, there is still the problem of latency on the ﬁrst miss. Figure 1.12

visualizes the situation for a simple vector norm kernel:

1 do i=1,N

2 S = S + A(i)

A(i)

3 enddo

There is only one load stream in this code. Assuming a cache line length of four

elements, three loads can be satisﬁed from cache before another miss occurs. The

long latency leads to long phases of inactivity on the memory bus.

Modern processors 21

Iteration #

time

cache miss: latency use data

use data

cache miss: latency

use data

Figure 1.12: Timing diagram on the inﬂuence of cache misses and subsequent latency penal-

ties for a vector norm loop. The penalty occurs on each new miss.

Making the lines very long will help, but will also slow down applications with

erratic access patterns even more. As a compromise one has arrived at typical cache

line lengths between 64 and 128 bytes (8–16 DP words). This is by far not big enough

to get around latency, and streaming applications would suffer not only from insufﬁ-

cient bandwidth but also from low memory bus utilization. Assuming a typical com-

modity system with a memory latency of 50ns and a bandwidth of 10GBytes/sec,

a single 128-byte cache line transfer takes 13 ns, so 80% of the potential bus band-

width is unused. Latency has thus an even more severe impact on performance than

bandwidth.

The latency problem can be solved in many cases, however, by prefetching. Pre-

fetching supplies the cache with data ahead of the actual requirements of an applica-

tion. The compiler can do this by interleaving special instructions with the software

pipelined instruction stream that “touch” cache lines early enough to give the hard-

ware time to load them into cache asynchronously (see Figure 1.13). This assumes

there is the potential of asynchronous memory operations, a prerequisite that is to

some extent true for current architectures. As an alternative, some processors feature

a hardware prefetcher that can detect regular access patterns and tries to read ahead

application data, keeping up the continuous data stream and hence serving the same

purpose as prefetch instructions. Whichever strategy is used, it must be emphasized

that prefetching requires resources that are limited by design. The memory subsys-

tem must be able to sustain a certain number of outstanding prefetch operations,

i.e., pending prefetch requests, or else the memory pipeline will stall and latency

cannot be hidden completely. We can estimate the number of outstanding prefetches

required for hiding thelatency completely: If T

ℓ

is the latency and B is the bandwidth,

the transfer of a whole line of length L

(in bytes) takes a time of

T = T

ℓ

. (1.5)

One prefetch operation must be initiated per cache line transfer, and the number of

cache lines that can be transferred during time T is the number of prefetches P that

22 Introduction to High Performance Computing for Scientists and Engineers

Iteration #

time

use data

cache miss: latency

Figure 1.13: Computation and data transfer can be overlapped much better with prefetching.

In this example, two outstanding prefetches are required to hide latency completely.

the processor must be able to sustain (see Figure 1.13):

P =

= 1+

ℓ

. (1.6)

As an example, for a cache line length of 128bytes (16 DP words), B =

10GBytes/sec and T

ℓ

= 50ns we get P≈5 outstanding prefetches. If this requirement

cannot be met, latency will not be hidden completely and the full memory bandwidth

will not be utilized. On the other hand, an application that executes so many ﬂoating-

point operations on the cache line data that they cannot be hidden behind the transfer

will not be limited by bandwidth and put less strain on the memory subsystem (see

Section 3.1 for appropriate performance models). In such a case, fewer outstanding

prefetches will sufﬁce.

Applications with heavy demands on bandwidth can overstrain the prefetch

mechanism. A second processor core using a shared path to memory can sometimes

provide for the missing prefetches, yielding a slight bandwidth boost (see Section 1.4

for more information on multicore design). In general, if streaming-style main mem-

ory access is unavoidable, a good programming guideline is to try to establish long

continuous data streams.

Finally, a note of caution is in order. Figures 1.12 and 1.13 stress the role of

prefetching for hiding latency, but the effects of bandwidth limitations are ignored.

It should be clear that prefetching cannot enhance available memory bandwidth, al-

though the transfer time for a single cache line is dominated by latency.

Modern processors 23

2 4 8 16

-0.6

-0.5

-0.4

-0.3

-0.2

-0.1

Figure 1.14: Required

relative frequency re-

duction to stay within a

given power envelope

on a given process tech-

nology, versus number

of cores on a multicore

chip (or package).

1.4 Multicore processors

In recent years it has become increasingly clear that, although Moore’s Law is

still valid and will probably be at least for the next decade, standard microproces-

sors are starting to hit the “heat barrier”: Switching and leakage power of several-

hundred-million-transistor chips are so large that cooling becomes a primary engi-

neering effort and a commercial concern. On the other hand, the necessity of an

ever-increasing clock frequency is driven by the insight that architectural advances

and growing cache sizes alone will not be sufﬁcient to keep up the one-to-one cor-

respondence of Moore’s Law with application performance. Processor vendors are

looking for a way out of this power-performance dilemma in the form of multicore

designs.

The technical motivation behind multicore is based on the observation that, for

a given semiconductor process technology, power dissipation of modern CPUs is

proportional to the third power of clock frequency f

(actually it is linear in f

and

quadratic in supply voltageV

, buta decrease in f

allows for a proportional decrease

inV

). Lowering f

and thusV

can therefore dramatically reduce power dissipation.

Assuming that a single core with clock frequency f

has a performance of p and a

power dissipation ofW, some relative change in performance

= ∆p/p will emerge

for a relative clock change of

= ∆f

/ f

. All other things being equal, |

| is an

upper limit for |

|, which in turn will depend on the applications considered. Power

dissipation is

W + ∆W = (1+

)

W . (1.7)

Reducing clock frequency opens the possibility to place more than one CPU core

on the same die (or, more generally, into the same package) while keeping the same

power envelope as before. For m “slow” cores this condition is expressed as

(1+

)

m = 1 =⇒

= m

−1/3

−1 . (1.8)

24 Introduction to High Performance Computing for Scientists and Engineers

L1D

Figure 1.15: Dual-core processor chip with

separate L1, L2, and L3 caches (Intel “Mon-

tecito”). Each core constitutes its own cache

group on all levels.

L1D L1D

L1D

PPPP

Figure 1.16: Quad-core processor

chip, con-

sisting of two dual-cores. Each dual-core

has shared L2 and separate L1 caches (Intel

“Harpertown”). There are two dual-core L2

groups.

Each one of those cores has the same transistor count as the single “fast” core, but

we know that Moore’s Law gives us transistors for free. Figure 1.14 shows the re-

quired relative frequency reduction with respect to the number of cores. The overall

performance of the multicore chip,

= (1+

)pm , (1.9)

should at least match the single-core performance so that

−1 (1.10)

is a limit on the performance penalty for a relative clock frequency reduction of

that should be observed for multicore to stay useful.

Of course it is not trivial to grow the CPU die by a factor of m with a given man-

ufacturing technology. Hence, the most simple way to multicore is to place separate

CPU dies in a common package. At some point advances in manufacturing tech-

nology, i.e., smaller structure lengths, will then enable the integration of more cores

on a die. Additionally, some compromises regarding the single-core performance of

a multicore chip with respect to the previous generation will be made so that the

number of transistors per core will go down as will the clock frequency. Some manu-

facturers have even adopted amore radical approach by designing new, much simpler

cores, albeit at the cost of possibly introducing new programming paradigms.

Finally, the over-optimistic assumption (1.9) that m cores show m times the per-

formance of a single core will only be valid in the rarest of cases. Nevertheless,

multicore has by now been adopted by all major processor manufacturers. In order to

avoid any misinterpretation we will always use the terms “core,” “CPU,” and “pro-

cessor” synonymously. A “socket” is the physical package in which multiple cores

(sometimes on multiple chips) are enclosed; it is usually equipped with leads or pins

so it can be used as a replaceable component. Typical desktop PCs have a single

socket, while standard servers use two to four, all sharing the same memory. See

Section 4.2 for an overview of shared-memory parallel computer architectures.