Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 765

An equilibrium point of (13.1) is a point x ∈ D satisfying f(x) = x or,

equivalently, s(k, x) = x for all k ∈ Z

. Unless otherwise stated, we assume

f(0) = 0 for I

= Z

. The following deﬁnition introduces several types

of stability corresponding to the zero solution x(k) ≡ 0 of the discrete-time

system (13.1) for I

= Z

Deﬁnition 13.1. i) The zero solution x(k) ≡ 0 to (13.1) is Lyapunov

stable if for all ε > 0 there exists δ = δ(ε) > 0 such that if kx(0)k < δ, then

kx(k)k < ε, k ∈ Z

ii) The zero solution x(k) ≡ 0 to (13.1) is asymptotically stable if it

is Lyapunov stable and there exists δ > 0 such that if kx(0)k < δ, then

lim

k→∞

x(k) = 0.

iii) The zero solution x(k) ≡ 0 to (13.1) is geometrically stable if there

exist positive constants α, β > 1, and δ such that if kx(0)k < δ, then

kx(k)k ≤ αkx(0)kβ

−k

, k ∈ Z

iv) The zero solution x(k) ≡ 0 to (13.1) is globally asymptotically stable

if it is Lyapunov stable and for all x(0) ∈ R

, lim

k→∞

x(k) = 0.

v) The zero solution x(k) ≡ 0 to (13.1) is globally geometrically stable if

there exist positive constants α and β > 1 su ch that kx(k)k ≤ αkx(0)kβ

−k

k ∈ Z

, for all x(0) ∈ R

vi) Finally, the zero solution x(k) ≡ 0 to (13.1) is unstable if it is not

Lyapunov s table.

The following result, known as Lyapunov’s direct m ethod, gives

suﬃcient conditions for Lyapu nov and asymptotic stability of a discrete-

time nonlinear dynamical s y s tem.

Theorem 13.2. Consider the discrete-time nonlinear dynamical sys-

tem (13.1) and assume that there exists a continuous function V : D → R

such that

V (0) = 0, (13.3)

V (x) > 0, x ∈ D, x 6= 0, (13.4)

V (f (x)) −V (x) ≤ 0, x ∈ D. (13.5)

Then the zero solution x(k) ≡ 0 to (13.1) is Lyapunov stable. If, in addition,

V (f (x)) −V (x) < 0, x ∈ D, x 6= 0, (13.6)

then the zero solution x(k) ≡ 0 to (13.1) is asymptotically stable.

Alternatively, if there exist scalars α, β > 0, ρ > 1, and p ≥ 1, such that

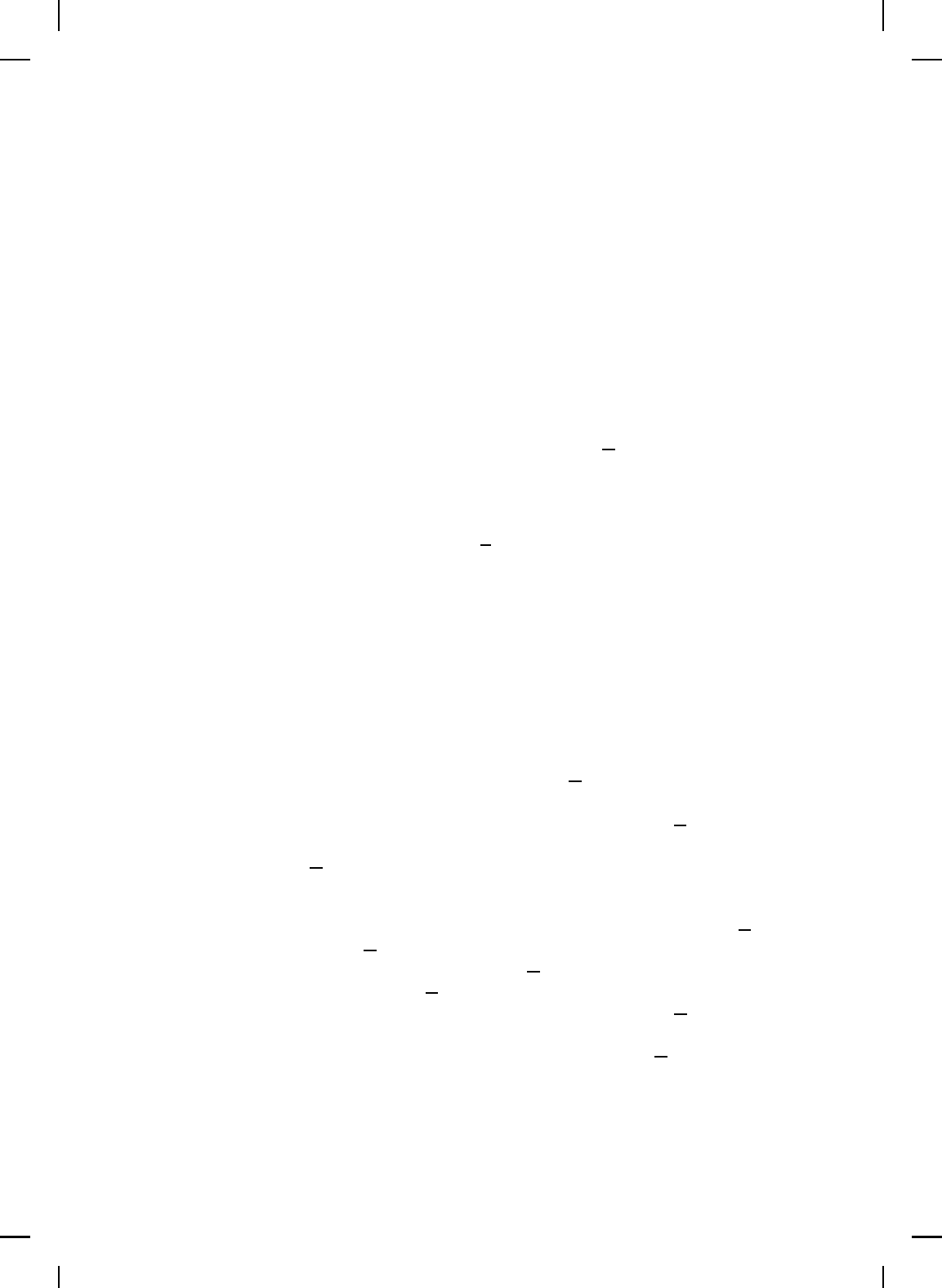
NonlinearBook10pt November 20, 2007

766 CHAPTER 13

V : D → R satisﬁes

αkxk

≤ V (x) ≤ βkxk

, x ∈ D, (13.7)

ρV (f (x)) ≤ V (x), x ∈ D, (13.8)

then the zero solution x(k) ≡ 0 to (13.1) is geometrically stable. Finally, if

D = R

and V (·) is s uch that

V (x) → ∞ as kxk → ∞ (13.9)

then (13.6) implies (respectively, (13.7) and (13.8) imply) that the zero

solution x(k) ≡ 0 to (13.1) is globally asymptotically (respectively, globally

geometrically) stable.

Proof. Let ε > 0 be such that B

(0) ⊆ D. S ince B

(0) is compact and

f(x), x ∈ D, is continuous, it follows that

△

= max

(

ε, max

x∈B

(0)

kf(x)k

)

(13.10)

exists. Next, let α

△

= min

x∈D: ε≤kxk≤η

V (x). Note α > 0 since 0 6∈ ∂B

(0)

and V (x) > 0, x ∈ D, x 6= 0. Next, let β ∈ (0, α) and deﬁne D

△

= {x ∈

(0) : V (x) ≤ β}. Now, for every x ∈ D

, it follows from (13.5) that

V (f (x)) ≤ V (x) ≤ β, and hence, it follows from (13.10) that kf (x)k ≤ η,

x ∈ D

. Next, suppose, ad absurdum, that there exists x ∈ D

such that

kf(x)k ≥ ε. This implies V (x) ≥ α, which is a contradiction. Hence, for

every x ∈ D

, it follows that f(x) ∈ B

(0) ⊂ D

, which implies that D

a positively invariant set (see Deﬁnition 13.4) with respect to (13.1). Next,

since V (·) is continuous and V (0) = 0, there exists δ = δ(ε) ∈ (0, ε) such

that V (x) < β, x ∈ B

(0). Now, let x(k), k ∈ Z

, satisfy (13.1). Since

(0) ⊂ D

⊂ B

(0) ⊆ D and D

is positively invariant with respect to

(13.1) it follows that for all x(0) ∈ B

(0), x(k) ∈ B

(0), k ∈ Z

. Hence,

for all ε > 0 there exists δ = δ(ε) > 0 su ch that if kx(0)k < δ, then

kx(k)k < ε, k ∈ Z

, which proves Lyapunov stability.

To prove asymptotic stability suppose that V (f(x)) < V (x), x ∈ D,

x 6= 0, and x(0) ∈ B

(0). Then it follows that x(k) ∈ B

(0), k ∈ Z

However, V (x(k)), k ∈ Z

, is decreasing and bounded from below by zero.

Now, suppose, ad absurdum, that x(k), k ∈ Z

, does not converge to zero.

This implies that V (x(k)), k ∈ Z

, is lower bounded by a positive number,

that is, there exists L > 0 such that V (x(k)) ≥ L > 0, k ∈ Z

. Hence,

by continuity of V (x), x ∈ D, there exists δ

′

> 0 such that V (x) < L for

x ∈ B

′

(0), which further implies that x(k) 6∈ B

′

(0), k ∈ Z

. Next, let

△

min

′

≤kxk≤ε

[V (x) − V (f(x))]. Now, (13.6) implies V (x) − V (f(x)) ≥ L

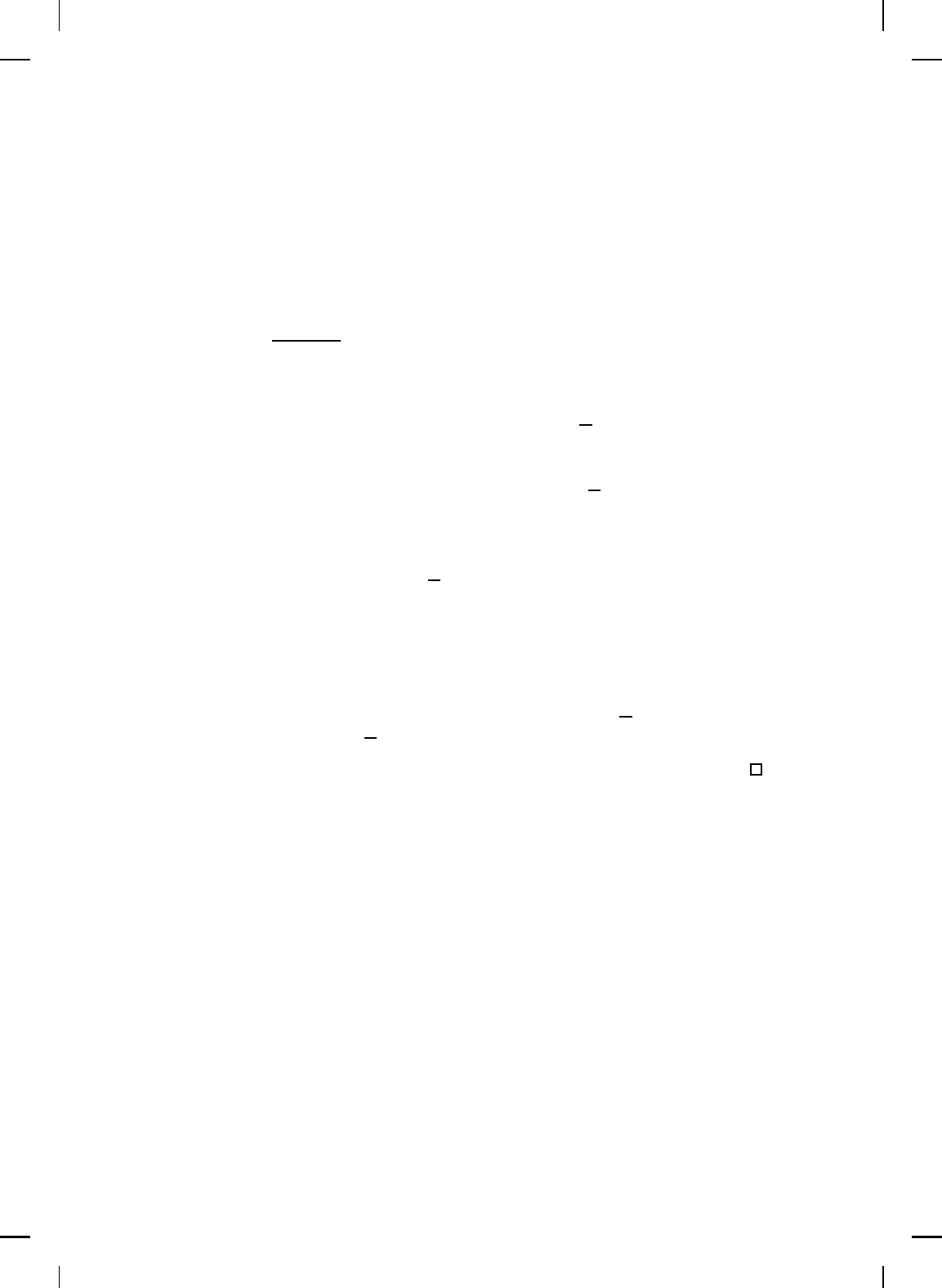
NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 767

′

≤ kxk ≤ ε, or, equivalently,

V (x(k)) − V (x(0)) =

k−1

i=0

[V (f(x(i))) −V (x(i))] ≤ −L

and h en ce, for all x(0) ∈ B

(0),

V (x(k)) ≤ V (x(0)) −L

Letting k >

V (x(0))−L

, it follows that V (x(k)) < L, which is a contradiction.

Hence, x(k) → 0 as k → ∞, establishing asymptotic stability.

Next, to show geometric stability note that (13.8) implies

V (x(k)) ≤ V (x(0))ρ

−k

, k ∈ Z

. (13.11)

Now, since V (x(0)) ≤ βkx(0)k

and αkx(k)k

≤ V (x(k)) it follows that

αkx(k)k

≤ βkx(0)k

−k

, k ∈ Z

, (13.12)

which implies that

kx(k)k ≤





1/p

kx(0)k(ρ

1/p

)

−k

, (13.13)

establishing geometric stability.

Finally, to prove global asymptotic and geometric stability, let x

∈ R

and β

△

= V (x

). Now, the rad ial unboundedness condition (13.9) implies

that there exists ε > 0 such that V (x) ≥ β for kxk ≥ ε, x ∈ R

. Hence,

it follows from (13.6) that V (x(k)) ≤ V (x(0)) = β, k ∈ Z

, which implies

that x(k) ∈ B

(0), k ∈ Z

. Now, the proof follows as in the proof of the

local results.

A continuous function V (·) satisfying (13.3) and (13.4) is called a

Lyapunov function candidate for the discrete-time nonlinear dynamical

system (13.1). If, additionally, V (·) satisﬁes (13.5), V (·) is called a Lyapunov

function f or th e discrete-time nonlinear dynamical system (13.1). Next, we

give a key deﬁnition involving the domain, or region, of attraction of the zero

solution x(k) ≡ 0 of the discrete-time nonlinear dynamical system (13.1).

Deﬁnition 13.2. Suppose the zero s olution x(k) ≡ 0 to (13.1) is

asymptotically stable. T hen the domain of attraction D

of (13.1) is given

△

= {x

∈ D : if x(0) = x

, then lim

k→∞

x(k) = 0}. (13.14)

As in the continuous-time case, constructing the actual domain of

attraction of a discrete-time nonlinear dynamical system is system trajectory

NonlinearBook10pt November 20, 2007

768 CHAPTER 13

dependent. To estimate a subset of the domain of attraction of the

dynamical system (13.1) assume there exists a continuous fun ction V :

D → R such that (13.3), (13.4), and (13.6) are satisﬁed. Next, let

△

= {x ∈ D : V (x) ≤ β}. Note that D

⊆ D and every trajectory

starting in D

will move to an inner energy surface, and hence, cannot

escape D

. Hence, D

is an estimate of the domain of attraction of the

nonlinear dynamical system (13.1). Now, to maximize this estimate of the

domain of attraction we maximize β such that D

⊆ D. Hence, deﬁne

△

= max{β > 0 : D

⊆ D} so that

△

= {x ∈ D : V (x) ≤ V

}, (13.15)

is a subset of th e d omain of attraction for (13.1) since ∆V (x)

△

= V (f (x)) −

V (x) < 0 for all x ∈ D

\{0} ⊆ D\{0}.

13.3 Discrete-Time Invariant Set Stability The orems

In this section, we use the discrete-time Barbashin-Krasovskii-LaSalle

invariance principle to relax on e of the conditions on the Lyapunov function

V (·) in the theorems given in Section 13.2. In particular, the strict negative-

deﬁniteness cond ition on the Lyapunov diﬀerence can be r elaxed while

ensuring system asymptotic stability. To state the main resu lts of this

section s everal deﬁnitions and a key lemma analogous to the ones given

in Section 2.12 are needed.

Deﬁnition 13.3. The trajectory x(k), k ∈ Z

, of (13.1) is bounded if

there exists γ > 0 such that kx(k)k < γ, k ∈ Z

Deﬁnition 13.4. A set M ⊂ D ⊆ R

is a positively invariant set for

the nonlinear dynamical system (13.1) if s

(M) ⊆ M, for all k ∈ Z

, wh ere

(M)

△

= {s

(x) : x ∈ M}. A set M ⊆ D ⊆ R

is an invariant set for th e

dynamical system (13.1) if s

(M) = M for all k ∈ Z

Deﬁnition 13.5. A point p ∈ D is a positive limit point of the

trajectory x(k), k ∈ Z

, of (13.1) if there exists a monotonic sequence

}

∞

n=0

of nonnegative numbers, with k

→ ∞ as n → ∞, such that

x(k

) → p as n → ∞. The set of all positive limit points of x(k), k ∈ Z

, is

the positive limit set ω(x

) of x(k), k ∈ Z

Note that if p ∈ D is a positive limit point of the trajectory x(·), then

for all ε > 0 and ﬁnite K ∈ Z

there exists k > K such that kx(k) −pk < ε.

This follows from the fact that kx(k) − pk < ε for all ε > 0 and some

k > K > 0 is equivalent to the existence of a sequence of integers {k

}

∞

n=0

with k

→ ∞ as n → ∞, such that x(k

) → p as n → ∞.

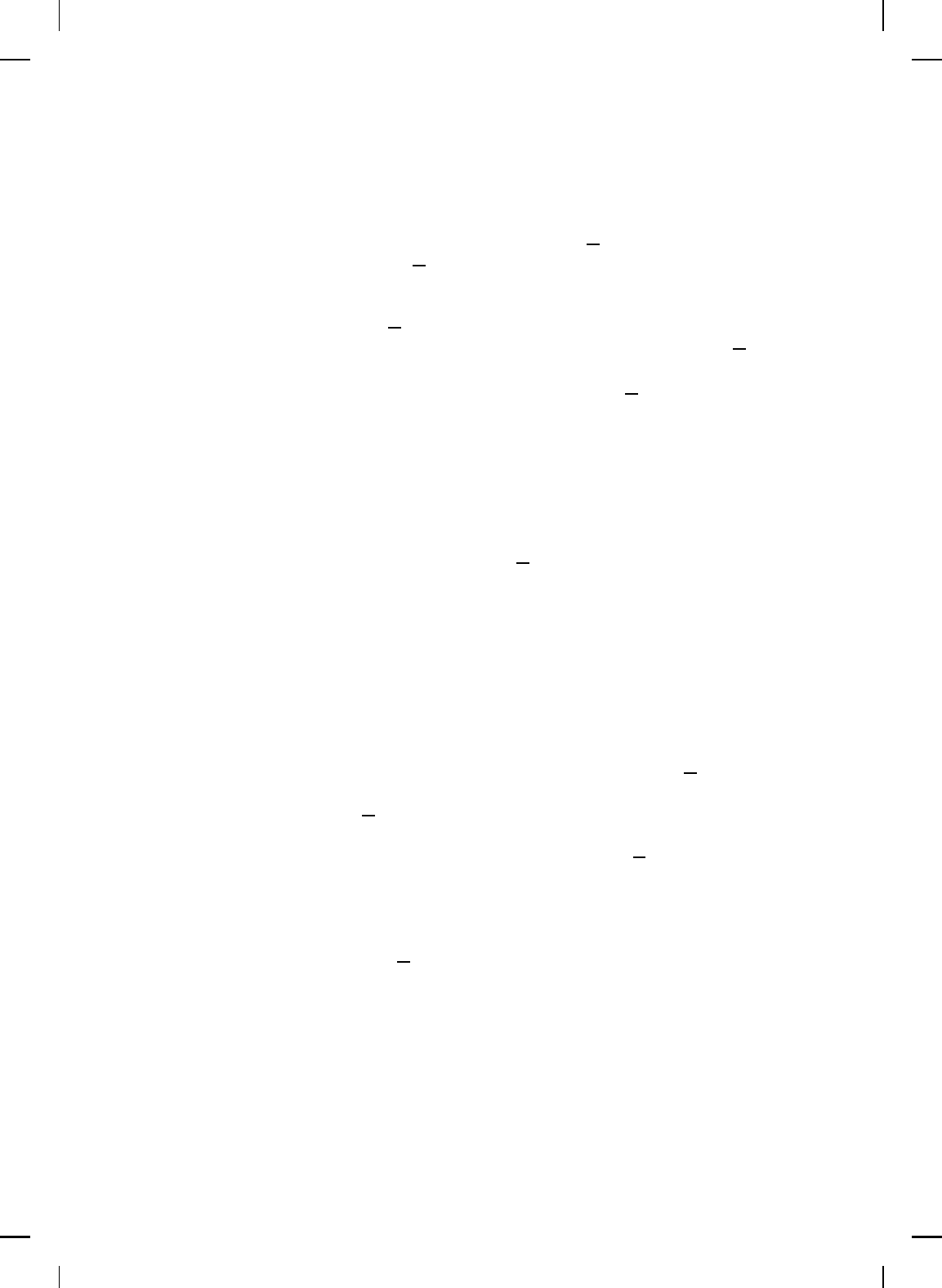
NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 769

Next, we state and prove a key lemma involving positive limit sets for

discrete-time systems.

Lemma 13.1. Suppose the solution x(k) to (13.1) corresponding to

an initial condition x(0) = x

is bounded for all k ∈ Z

. Then the positive

limit set ω(x

) of x(k), k ∈ Z

, is a nonempty, compact, invariant set.

Furth ermore, x(k) → ω(x

) as t → ∞.

Proof. Let x(k), k ∈ Z

, denote the solution to (13.1) corresponding

to the initial condition x(0) = x

. Next, since x(k) is bounded for all k ∈ Z

it follows from the Bolzano-Weierstrass theorem (Theorem 2.3) that every

sequence in the positive orbit O

△

= {s(k, x

) : k ∈ Z

} h as at least

one accumulation point p ∈ D as k → ∞, and hence, ω(x

) is nonempty.

Next, let p ∈ ω(x

) so that there exists an in creasing unbounded sequence

}

∞

n=0

, with k

= 0, such that lim

n→∞

x(k

) = p. Now, since x(k

) is

uniformly bounded in n it follows that the limit point p is bounded, which

implies that ω(x

) is bounded. To show that ω(x

) is closed let {p

}

∞

i=0

be a

sequence contained in ω(x

) such that lim

i→∞

= p. Now, since p

→ p as

i → ∞ for every ε > 0, there exists i such that kp − p

k < ε/2. Next, since

∈ ω(x

), there exists k ≥ K, where K ∈ Z

is arbitrary and ﬁnite, s uch

that kp

− x(k)k < ε/2. Now, since kp − p

k < ε/2 and kp

− x(k)k < ε/2,

k ≥ K, it follows that kp − x(k)k ≤ kp

− x(k)k + kp − p

k < ε. Thus,

p ∈ ω(x

). Hence, every accumulation point of ω(x

) is an element of

ω(x

) so that ω(x

) is closed. Thus, sin ce ω(x

) is closed an d bounded it is

compact.

To sh ow positive invariance of ω(x

) let p ∈ ω(x

) so that there exists

an increasing sequence {k

}

∞

n=0

such th at x(k

) → p as n → ∞. Now, let

s(k

, x

) denote the solution x(k

) of (13.1) with initial condition x(0) = x

and note that since f : D → D in (13.1) is continuous, x(k), k ∈ Z

, is the

unique solution to (13.1) so that s(k+k

, x

) = s(k, s(k

, x

)) = s(k, x(k

)).

Now, since s(k, x

), k ∈ Z

, is continuous with respect to x

, it follows that,

for k + k

≥ 0, lim

n→∞

s(k + k

, x

) = lim

n→∞

s(k, x(k

)) = s(k, p), and

hence, s(k, p) ∈ ω(x

). Hence, s

(ω(x

)) ⊆ ω(x

), k ∈ Z

, establishing

positive invariance of ω(x

To show invariance of ω(x

) let y ∈ ω(x

) so that there exists

an in creasing unbounded sequence {k

}

∞

n=0

such that s(k

, x

) → y as

n → ∞. Next, let k ∈ Z

and note that th ere exists N such that

> k, n ≥ N. Hence, it follows from th e semigroup property that

s(k, s(k

− k, x

)) = s(k

, x

) → y as n → ∞. Now, it follows from the

Bolzano-Lebesgue theorem (Theorem 2.4) that there exists a subsequence

of the sequence z

= s(k

− k, x

), n = N, N + 1, . . ., such that

→ z ∈ D and, by deﬁn ition, z ∈ ω(x

). Next, it follows from th e

NonlinearBook10pt November 20, 2007

770 CHAPTER 13

continuous depen dence property that lim

i→∞

s(k, z

) = s(k, lim

i→∞

and hence, y = s(t, z), which implies th at ω(x

) ⊆ s

(ω(x

)), k ∈ Z

. Now,

using positive invariance of ω(x

) it follows that s

(ω(x

)) = ω(x

), k ∈ Z

establishing invariance of the positive limit set ω(x

Finally, to show x(k) → ω(x

) as k → ∞, suppose, ad absurdum, that

x(k) 6→ ω(x

) as k → ∞. In this case, there exists a sequence {k

}

∞

n=0

, with

→ ∞ as n → ∞, such that

inf

p∈ω(x

)

kx(k

) − pk > ε, n ∈ Z

. (13.16)

However, since x(k), k ∈ Z

, is bounded, the bounded sequence {x(k

)}

∞

n=0

contains a convergent s ubsequence {x(k

∗

)}

∞

n=0

such that x(k

∗

) → p

∗

∈ ω(x

)

as n → ∞, which contradicts (13.16). Hence, x(k) → ω(x

) as k → ∞.

Next, we present a discrete-time version of the Barbashin-Krasovskii-

LaSalle invariance principle.

Theorem 13.3. Consider the discrete-time nonlinear dynamical sys-

tem (13.1), assume D

is a compact invariant set with respect to (13.1),

and assume that there exists a continuous function V : D

→ R such that

V (f (x)) − V (x) ≤ 0, x ∈ D

. Let R

△

= {x ∈ D

: V (f(x)) = V (x)} and

let M denote the largest invariant set contained in R. If x(0) ∈ D

, then

x(k) → M as k → ∞.

Proof. Let x(k), k ∈ Z

, be a solution to (13.1) with x(0) ∈ D

. Sin ce

V (f (x)) ≤ V (x), x ∈ D

, it follows that

V (x(k)) − V (x(κ)) =

k−1

i=κ

[V (f(x(i))) − V (x(i))] ≤ 0, k − 1 ≥ κ,

and hence, V (x(k)) ≤ V (x(κ)), k − 1 ≥ κ, which implies that V (x(k))

is a nonincreasing function of k. Next, since V (x) is continuous on the

compact set D

, there exists L ≥ 0 such that V (x) ≥ L, x ∈ D

. Hence,

△

= lim

k→∞

V (x(k)) exists. Now, for all p ∈ ω(x

) there exists an

increasing unbounded sequence {k

}

∞

n=0

, with k

= 0, such th at x(k

) → p

as n → ∞. Since V (x), x ∈ D, is continuous, V (p) = V (lim

n→∞

x(k

)) =

lim

n→∞

V (x(k

)) = γ

, and hence, V (x) = α on ω(x

). Now, since D

is compact and invariant it follows that x(k), k ∈ Z

, is bounded, and

hence, it follows from Lemma 13.1 that ω(x

) is a nonempty, compact

invariant set. Hence, it f ollows that V (f(x)) = V (x) on ω(x

), and hence,

ω(x

) ⊂ M ⊂ R ⊂ D

. Finally, since x(k) → ω(x

) as k → ∞ it follows

that x(k) → M as k → ∞.

Now, using Theorem 13.3 we provide a generalization of Theorem 13.2

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 771

for local asymptotic s tability of a nonlinear dynamical s y stem.

Corollary 13.1. Consider the nonlinear dynamical system (13.1),

assume D

is a compact invariant set with respect to (13.1) such that 0 ∈

◦

and assume that there exists a continuous function V : D

→ R such that

V (0) = 0, V (x) > 0, x 6= 0, and V (f(x)) − V (x) ≤ 0, x ∈ D

. Furth ermore,

assume that the set R

△

= {x ∈ D

: V (f(x)) = V (x)} contains no invariant

set other than the set {0}. Then the zero solution x(k) ≡ 0 to (13.1) is

asymptotically stable and D

is a subset of the domain of attraction of

(13.1).

Proof. The resu lt is a direct consequence of Theorem 13.3.

In Theorem 13.3 and Corollary 13.1 we explicitly assumed that there

exists a compact invariant set D

⊂ D of (13.1). Next, we provide a result

that does not require the existence of a compact invariant set D

Theorem 13.4. Consider the nonlinear dynamical system (13.1) and

assume that there exists a continuous function V : R

→ R such that

V (0) = 0, (13.17)

V (x) > 0, x ∈ R

, x 6= 0, (13.18)

V (f (x)) −V (x) ≤ 0, x ∈ R

. (13.19)

Let R

△

= {x ∈ R

: V (f(x)) = V (x)} and let M be the largest invariant set

contained in R. Then all solutions x(k), k ∈ Z

, to (13.1) that are bounded

approach M as k → ∞.

Proof. Let x ∈ R

be such that trajectory s(k, x), k ∈ Z

, of (13.1) is

bounded. Now, with D

= O

, it follows from Theorem 13.3 that s(k, x) →

M as k → ∞.

Next, we present the global invariant set theorem for guaranteeing

global asymptotic stability of a discrete-time nonlinear dynamical system.

Theorem 13.5. Consider the nonlinear dynamical system (13.1) and

assume that there exists a continuous function V : R

→ R such that

V (0) = 0 (13.20)

V (x) > 0, x ∈ R

, x 6= 0, (13.21)

V (f (x)) −V (x) ≤ 0, x ∈ R

, (13.22)

V (x) → ∞ as kxk → ∞. (13.23)

Furth ermore, assume that the set R

△

= {x ∈ R

: V (f(x)) = V (x)} contains

no invariant set other than th e set {0}. Then the zero solution x(k) ≡ 0 to

NonlinearBook10pt November 20, 2007

772 CHAPTER 13

(13.1) is globally asymptotically stable.

Proof. Since (13.20)–(13.22) hold, it follows from Theorem 13.2 that

the zero solution x(k) ≡ 0 to (13.1) is Lyapunov stable wh ile the radial

unboundedness condition (13.23) implies that all solutions to (13.1) are

bounded. Now, Theorem 13.4 implies that x(k) → M as k → ∞. However,

since R contains no invariant set other than the set {0}, the set M is {0},

and h en ce, global asymptotic stability is immediate.

13.4 Con verse Lyapunov Theorems for Discrete-Time Systems

In the previous sections the existence of a Lyapunov function is assumed

while stability properties of a discrete-time nonlinear dynamical system are

deduced. As in the continuous-time case, the existence of a lower semi-

continuous and continuous time-invariant Lyapunov function for Lyapunov

stable and asymptotically stable, respectively, discrete-time s ystems can be

established. In order to state and prove the converse Lyapunov theorems

for discrete-time systems the following key lemma is needed.

Lemma 13.2. Let σ : Z

→ Z

be a class L function. Then there

exists a continuous class K function γ : Z

→ Z

such that

∞

k=0

γ[σ(k)] <

∞.

Proof. The proof is similar to the proof of Lemm a 3.1 and, hence, is

omitted.

Theorem 13. 6. Assume that the zero solution x(k) ≡ 0 to (13.1) is

Lyapunov (respectively, asymptotically) stable and f : D → D is continuous.

Then there exist a set D

⊆ D with 0 ∈

◦

and a lower semi-continuous

(respectively, continuous) function V : D

→ R

such that V (·) is continuous

at the origin, V (0) = 0, V (x) > 0, x ∈ D

, x 6= 0, and V (f(x)) ≤ V (x),

x ∈ D

(respectively, V (f(x)) −V (x) < 0, x ∈ D

, x 6= 0).

Proof. Let ε > 0. Since th e zero solution x(k) ≡ 0 to (13.1)

is Lyapunov stable it follows that there exists δ > 0 such that if x

∈

(0), then s(k, x

) ∈ B

(0), k ∈ Z

. Now, let D

= {y ∈ B

(0) :

there exist k ∈ Z

and x

∈ B

(0) such that y = s(k, x

)}, that is, D

(0)). Note that D

⊆ B

(0), D

is positively invariant, and B

(0) ⊆ D

Hence, 0 ∈

◦

. Next, deﬁne V (x)

△

= sup

k∈Z

ks(k, x)k, x ∈ D

, and since

is positively invariant and bounded it follows that V (·) is well deﬁned

on D

. Now, x = 0 implies s(k, x) ≡ 0, and hence, V (0) = 0. Furthermore,

V (x) ≥ ks(0, x)k = kxk > 0, x ∈ D

, x 6= 0.

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 773

Next, since f(·) in (13.1) is continuous, it follows that for every x ∈ D

s(k, x), k ∈ Z

, is the un ique solution to (13.1) so that s(k, x) = s(k −

κ, s(κ, x)), 0 ≤ κ ≤ k, which implies that for every k, κ ∈ Z

, such that

k ≥ κ,

V (s(κ, x)) = sup

θ∈Z

ks(θ, s(κ, x))k

= sup

θ∈Z

ks(κ + θ, x)k

≥ sup

θ≥k−κ

ks(κ + θ, x)k

= sup

θ≥k−κ

ks(θ − (k − κ), s(k, x))k

= sup

θ∈Z

ks(θ, s(k, x))k

= V (s(k, x)), (13.24)

which proves that V (f(x)) −V (x) = V (s(1, x)) −V (s(0, x)) ≤ 0.

Next, since the zero solution x(k) ≡ 0 to (13.1) is Lyapunov stable it

follows that for every ˆε > 0 there exists

δ > 0 such that if x

∈ B

(0), then

s(k, x

) ∈ B

ˆε/2

(0), k ∈ Z

, which implies that V (x

) = sup

k∈Z

ks(k, x

)k ≤

ˆε/2. Hence, for every ˆε > 0 th ere exists

δ > 0 such that if x

∈ B

(0), then

V (x

) < ˆε, establishing that V (·) is continuous at the origin. Finally, to

show that V (·) is lower semicontinuous everywhere on D

, let x ∈ D

and

let ˆε > 0, and since V (x) = sup

k∈Z

ks(k, x)k there exists K = K(x, ˆε) > 0

such that V (x)−ks(K, x)k < ˆε. Now, consider a sequence {x

}

∞

i=1

∈ D

such

that x

→ x as i → ∞. Next, since f(·) in (13.1) is continuous, it follows

that for every k ∈ Z

, s(k, ·) is continuous. Hence, since k · k : D

→ R is

continuous, ks(K, x)k = lim

i→∞

ks(K, x

)k, which implies that

V (x) < ks(K, x)k + ˆε

= lim

i→∞

ks(K, x

)k + ˆε

≤ lim inf

i→∞

sup

k∈Z

ks(k, x

)k + ˆε

= lim inf

i→∞

V (x

) + ˆε, (13.25)

which, since ˆε > 0 is arbitrary, f urther implies that V (x) ≤ lim inf

i→∞

V (x

). Thus, since {x

}

∞

i=1

is arbitrary sequence converging to x, it follows

that V (·) is lower semicontinuous on D

Next, assume that the zero solution x(k) ≡ 0 to (13.1) is asymptot-

ically stable. It follows that (see Problem 3.76) there exist class K and L

functions α(·) and β(·), respectively, such that if kx

k < δ, for some δ > 0,

then kx(k)k ≤ α(kx

k)β(k), k ∈ Z

. Next, let x ∈ B

(0) and let s(k, x)

NonlinearBook10pt November 20, 2007

774 CHAPTER 13

denote the solution to (13.1) with the initial condition x(0) = x so that for

all kxk < δ, ks(k, x)k ≤ α(kxk)β(k), k ∈ Z

. Now, it follows from Lemma

13.2 that th ere exists a continuous class K function γ : R

→ R

such that

∞

k=0

γ(α(δ)β(k)) < ∞. Since ks(k, x)k ≤ α(kxk)β(k) ≤ α(δ)β(k), k ∈ Z

it follows that the function

V (x) =

∞

k=0

γ(ks(k, x)k),

is well deﬁned on D. Furthermore, note that V (0) = 0. Next, note that

V (x) =

∞

k=0

γ( ks(k, x)k) > 0, x ∈ D, x 6= 0. Finally, note that since f(·)

is continuous the trajectory s(k, x), k ∈ Z

, is unique, and hence,

V (s(k, x)) =

∞

κ=0

γ(ks(κ, s(k, x))k)

∞

κ=0

γ(ks(κ + k, x)k)

∞

κ=k

γ(ks(κ, x)k),

which implies that V (f(x))−V (x) = V (s(1, x))−V (s(0, x)) = −γ(kxk) < 0,

x ∈ D

, x 6= 0. The result is now immediate by noting that V : D → R

deﬁned above is continuous.

The next result gives a converse Lyapunov theorem f or geometric

stability.

Theorem 13. 7. Assume that the zero solution x(k) ≡ 0 to (13.1) is

geometrically stable and f : D → D is continuous. Then, for every p > 1,

there exist a set D

⊆ D with 0 ∈

◦

, a continuous function V : D

→ R,

and scalars α, β > 0, β > α, and ρ > 1 such that

αkxk

≤ V (x) ≤ βkxk

, x ∈ D

, (13.26)

ρV (f (x)) ≤ V (x), x ∈ D

. (13.27)

Proof. Since the zero solution x(k) ≡ 0 to (13.1) is, by assumption,

geometrically stable it follows that there exist scalars α

≥ 1, β

> 1,

and δ > 0 such that if kx

k < δ, then kx(k)k ≤ α

kβ

−k

, k ∈ Z

Next, let x ∈ B

(0) and let s(k, x) denote the solution to (13.1) with the

initial condition x(0) = x so that for all kxk < δ, ks(k, x)k ≤ α

kxkβ

−k

k ∈ Z

. Now, using identical arguments as in Theorem 13.6 it follows that