Гулякина Н.А. Общая теория систем

Подождите немного. Документ загружается.

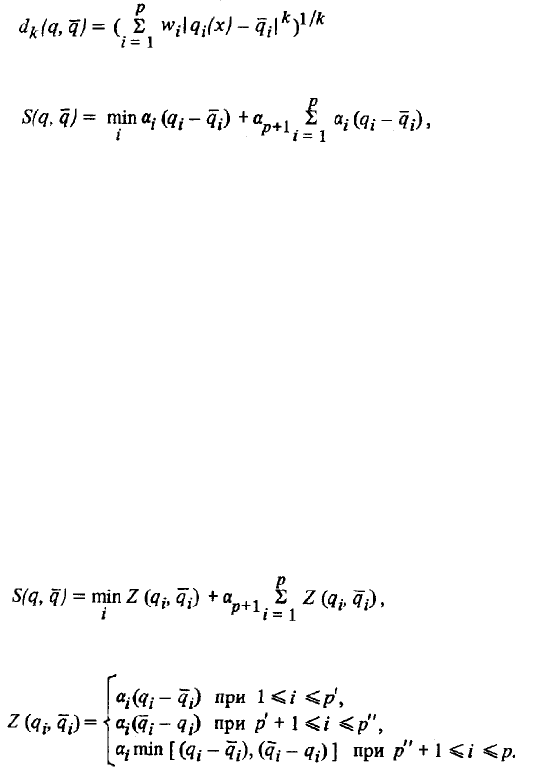
количественно описать эту близость. Например, использовав

расстояния типа

либо расстояния типа

где считается, что q

>= !q

, a

- коэффициенты, приводящие

слагаемые к одинаковой размерности и одновременно учитывающие

разноважность критериев, а

p+1

выражает наше отношение к тому, что

важнее - уменьшать близость к цели любого из частных критериев или

суммарную близость всех критериев к целевым значениям. Если часть

уровней притязания ограничивают критерии снизу (q

>= !q

, i = 1,...,

р'), часть ограничивают их сверху (q

<= !q

, i = р'+ 1, ..., р"), а

остальные задают их жестко (q

= !q

, i = р"+ 1,..., р), то функцию S(q, !

q) модифицируют:

где

Конечно, возможны и другие меры близости, но для функций d(q,

!q) и S(q, !q) проведены подробные исследования их математических

свойств, что важно для обеспечения сходимости процесса

минимизации этих функций, в ходе которого обеспечивается

приближение к x*.

Тема 9.4 НАХОЖДЕНИЕ ПАРЕТОВСКОГО МНОЖЕСТВА

Четвертый полностью формализуемый способ

многокритериального выбора состоит в отказе от выделения

единственной "наилучшей" альтернативы и соглашении о том, что

предпочтение одной альтернативе перед другой можно отдавать только

если первая по всем критериям лучше второй. Если же предпочтение

хотя бы по одному критерию расходится с предпочтением по другому,

то такие альтернативы признаются несравнимыми. В результате

попарного сравнения альтернатив все худшие по всем критериям

альтернативы отбрасываются, a все оставшиеся несравнимые между

собой (недоминируемые) принимаются. Если все максимально

достижимые значения частных критериев относятся к одной и той же

альтернативе, то принятые альтернативы образуют множество Парето и

выбор на этом заканчивается. На рис. 9.1, г жирной линией выделено

множество Парето для рассматриваемого примера. При необходимости

же выбора единственной альтернативы следует привлекать

дополнительные соображения: вводить новые добавочные критерии и

ограничения, либо бросать жребий, либо прибегать к услугам

экспертов.

Мы обсудили наиболее употребительные способы описания

выбора в терминах критериального языка. Возможны и другие

постановки задач на этом языке; наша цель состояла в том, чтобы дать

лишь общее представление об их многообразии. Для обозримости и

облегчения запоминания приведем схему совокупности изложенных

способов (рис. 9.2).

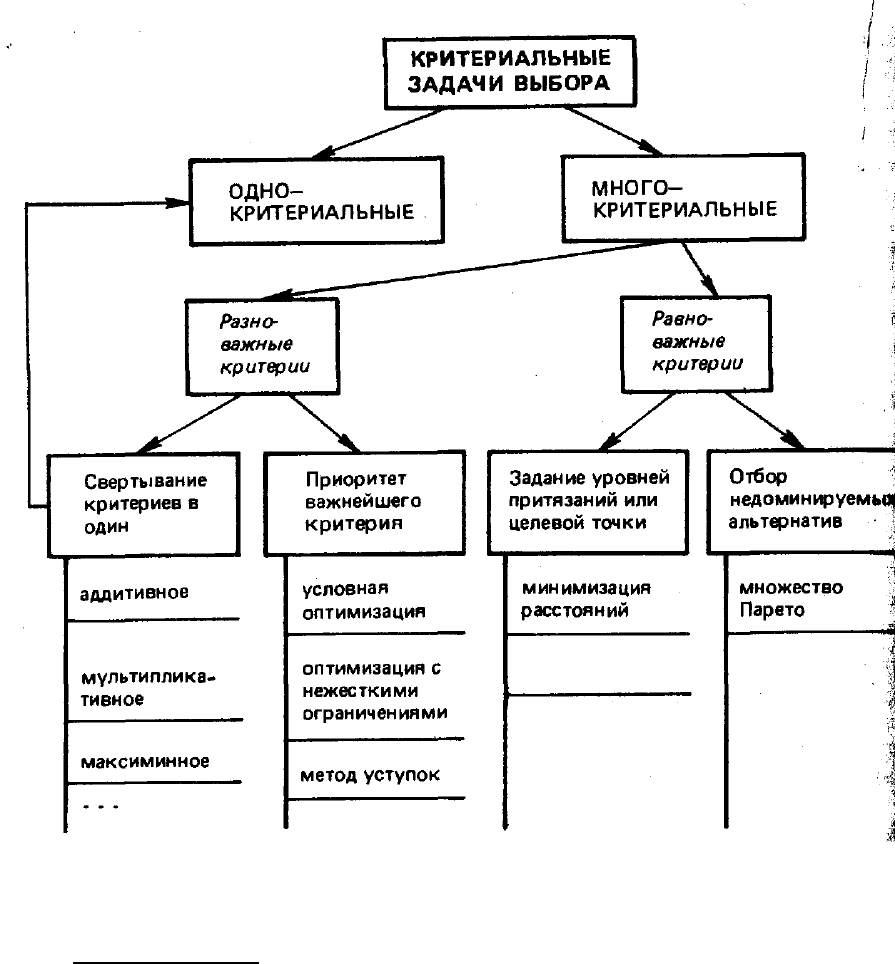
Рисунок 9.2. Классификация задач выбора и способов их решения

при их описании на критериальном языке

Подведем итог:

Основой критериального языка описания выбора является

предположение о возможности оценить каждую отдельно взятую

альтернативу определенным числом. При этом выбор сводится к

отысканию альтернативы с наибольшим значением критериальной

функции. Многокритериальные задачи не имеют однозначного общего

решения. Поэтому предлагается много разных способов придать

многокритериальной задаче частный вид, обладающий единственным

решением. Естественно, что для разных способов эти решения в общем

случае оказываются различными. Поэтому едва ли не главное в

решении многокритериальной задачи — обоснование именно данного

вида ее постановки.

Тема 9.5 ОПИСАНИЕ ВЫБОРА НА ЯЗЫКЕ БИНАРНЫХ

ОТНОШЕНИЙ

Второй, более общий язык, на котором описывается выбор, —

это язык бинарных отношений. Его большая, нежели у критериального

языка, общность основана на учете того факта, что в реальности дать

оценку отдельно взятой альтернативе часто затруднительно или

невозможно; однако если рассматривать ее не в отдельности, а в паре с

другой альтернативой, то находятся основания сказать, какая из них

более предпочтительна.

Таким образом, основные предположения этого языка сводятся к

следующему:

1) отдельная альтернатива не оценивается, т.е.

критериальная функция не вводится;

2) для каждой пары альтернатив (х, у) некоторым образом

можно установить, что одна из них предпочтительнее другой либо они

равноценны или несравнимы (чаще всего последние два понятия

отождествляются);

3) отношение предпочтения внутри любой пары

альтернатив не зависит от остальных альтернатив, предъявленных к

выбору.

Математически бинарное отношение R на множестве X

определяется как определенное подмножество упорядоченных пар (х,

у). Удобно использовать обозначение xRy, если х находится в

отношении R с у, x!Ry в противном случае. Множество всех пар {(х, у),

х, у  X} называется полным ("универсальным") бинарным

отношением. Поскольку в общем случае не все возможные пары (х, у)

удовлетворяют условиям накладываемым отношением R, бинарное

отношение является некоторым подмножеством полного бинарного

отношения, т.е. R  Х* Х.

Задать отношение — это значит тем или иным способом указать

все пары (х, у), для которых выполнено отношение R.

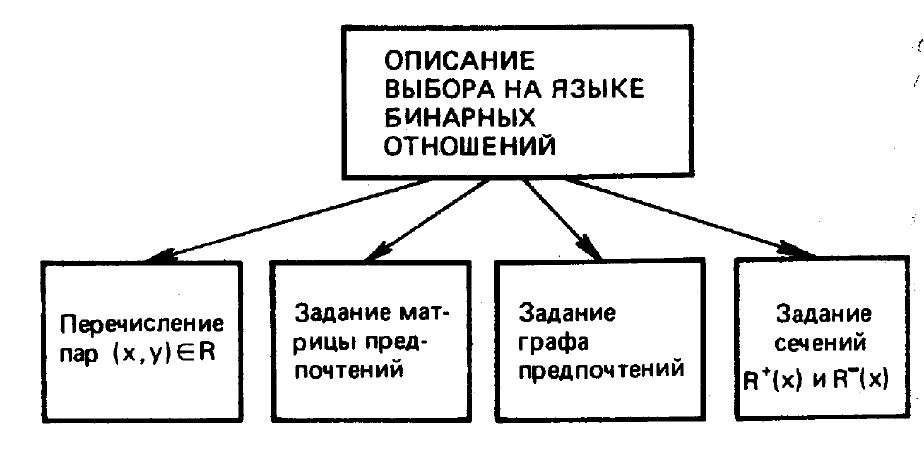
Существует четыре разных способа задания отношений (рис. 9.3)

преимущества каждого проявляются при разных характеристиках

множества X.

Рисунок9.3. Способы описания выбора на языке бинарных

отношений

Первый, очевидный, способ состоит в непосредственном

перечислении таких пар. Ясно, что он приемлем лишь в случае

конечного множества X.

Второй удобный способ задания отношения R на конечном

множестве — матричный. Все элементы нумеруются, и матрица

отношения R определяется своими элементами а

(R) = {1: x

; 0:

!Rx

} для всех i и j. Известным примером такого задания отношений

являются турнирные таблицы (если ничьи обозначить нулями, как и

проигрыш, то матрица изобразит отношение "x

, — победитель х

").

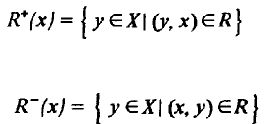
Третий способ — задание отношения графом. Вершинам графа G

(R) ставят в соответствие (пронумерованные) элементы множества X, и

если x

, то от вершины x

проводят направленную дугу к вершине

; если же x

!Rx

, то дуга отсутствует.

Для определения отношений на бесконечных множествах

используется четвертый способ — задание отношение R сечениями.

Множество

называется верхним сечением отношения R, а множество

- нижним сечением. Иначе говоря, верхнее сечение — это

множество всех у  X, которые находятся в отношении yRx с

заданным элементом х  Х, а нижнее сечение — множество всех y

X, с которыми заданный элемент х находится в отношении R.

Отношение однозначно определяется одним из своих сечений.

Для теории выбора особое значение среди всех бинарных

отношений имеют отношения, которые соответствуют предпочтению

одной альтернативы перед другой или случаю невозможности отдать

предпочтение одной из двух альтернатив. Эти отношения можно задать

через строго определяемые отношения эквивалентности, порядка и

доминирования. Для их определения нам понадобятся некоторые

свойства отношений вообще.

Бинарное отношение R на множестве называется:

 рефлексивным, если xRx для каждого х  X;

 антирефлексивным, если x!Rxx  X (т.е. R может

выполняться только для несовпадающих элементов);

 симметричным, если xRy -> yRx х, v  X;

 асимметричным, если xRy -> y!Rx  х, у  X (ясно, что

асимметричное отношение R антирефлексивно);

 антисимметричным, если для всех x, у  X (xRy, yRx) -> х

= у;

 транзитивным, если для всех х, y, z  X (xRy, yRz) -> xRz;

 отрицательно транзитивным, если отношение !R

транзитивно;

 сильно транзитивным, если отношение одновременно

транзитивно и отрицательно транзитивно.

Теперь можно охарактеризовать отношения, используемые в

теории выбора.

Отношение R на множестве Х называет отношением

эквивалентности (обозначение ~), если оно рефлексивно, симметрично

и транзитивно. Примеры отношений эквивалентности "быть четным",

"иметь одинаковый остаток от деления на 3" - на множестве

натуральных чисел; "быть одноклассниками" — на множестве

учеников данной школы; "быть подобными" — на множестве

многоугольников. Задание отношения эквивалентности равносильно

разбиению множества Х на непересекающиеся классы (X =  X

, X



= ф при ij) эквивалентных элемнтов: x ~ y тогда и только тогда,

когда х, y  X

(т.е. если x и y принадлежат одномк классу

эквивалентности).

Отношением нестрогого порядка (обозначение <=) называется

рефлексивное, антисимметричное и транзитивное отношение.

Отношением строгого порядка (обозначение <) называется

антирефлексивное, асимметричное и транзитивное отношение.

Отношение нестрогого порядка можно рассматривать как объединение

отношений < и ~.

Наконец, отношением доминирования называется отношение,

обладающее антирефлексивностью и асимметричностью. Говорят, что

"х доминирует у" (обозначается х >> у), когда х в каком-то смысле

превосходит у. (Очевидно, строгий порядок — частный случай

доминирования, при котором имеет место еще транзитивность.)

Хотя при подробном рассмотрении выбора потребуются и другие

факты теории отношений, введенные понятия позволяют составить

представление о возможностях данного языка.

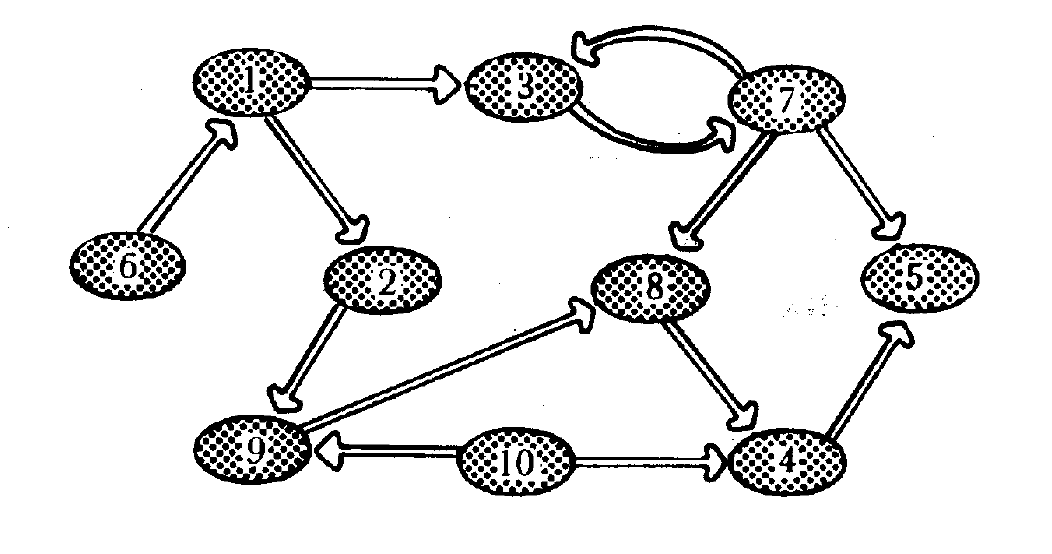
В случае конечных множеств Х очень удобно находить

наилучшие альтернативы с помощью графа предпочтений, стрелки

которого направлены в сторону менее предпочтимой альтернативы

(рис. 9.4). Выделив вершины графа, из которых стрелки только исходят

(альтернативы б и 10 на рис. 9.4), мы находим недоминируемые, т.е.

наилучшие, альтернативы. Можно показать, что если граф сильно

транзитивен (т.е. транзитивен и по наличию, и по отсутствию стрелок)

и антирефлексивен (отсутствуют петли), то описываемый выбор

сводится к однокритериальному выбору. Другие типы графов

описывают другие ситуации выбора.

Рисунок 9.4 Пример графа предпочтений

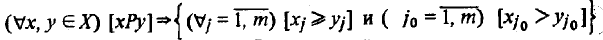
Несмотря на то что язык бинарных отношений введен для

описания более общих и сложных ситуаций, нежели те, которые

описываются критериальным языком, в чисто познавательных целях

поучительно проследить, как уже известная нам ситуация выглядит в

новом представлении.

Например, многомерное критериальное пространство (с теми

оговорками о соотношении размерностей критериев, которые были

сделаны в предыдущем параграфе) может быть поставлено в

соответствие евклидову пространству. Введение на этом пространстве

бинарных отношений требует учета его свойств. В частности,

начинают играть роль отношения инвариантные (относительно

переноса), для которых верхнее сечение в любой точке может быть

получено параллельным переносом верхнего сечения в любой другой

точке. Примером инвариантного отношения является отношение

Парето Р:

Верхнее сечение отношения Р есть первый квадрант с началом в

точке теперь понятно, как находится паретовское множество

альтернатив (на рис. 9.5 приведен случай конечного множества X;

сравните этот рисунок с рис. 9.1, г): в паретовское множество

включаются альтернативы, верхнее сечение которых пусто (на рис. 9.6

они отмечены кружками).

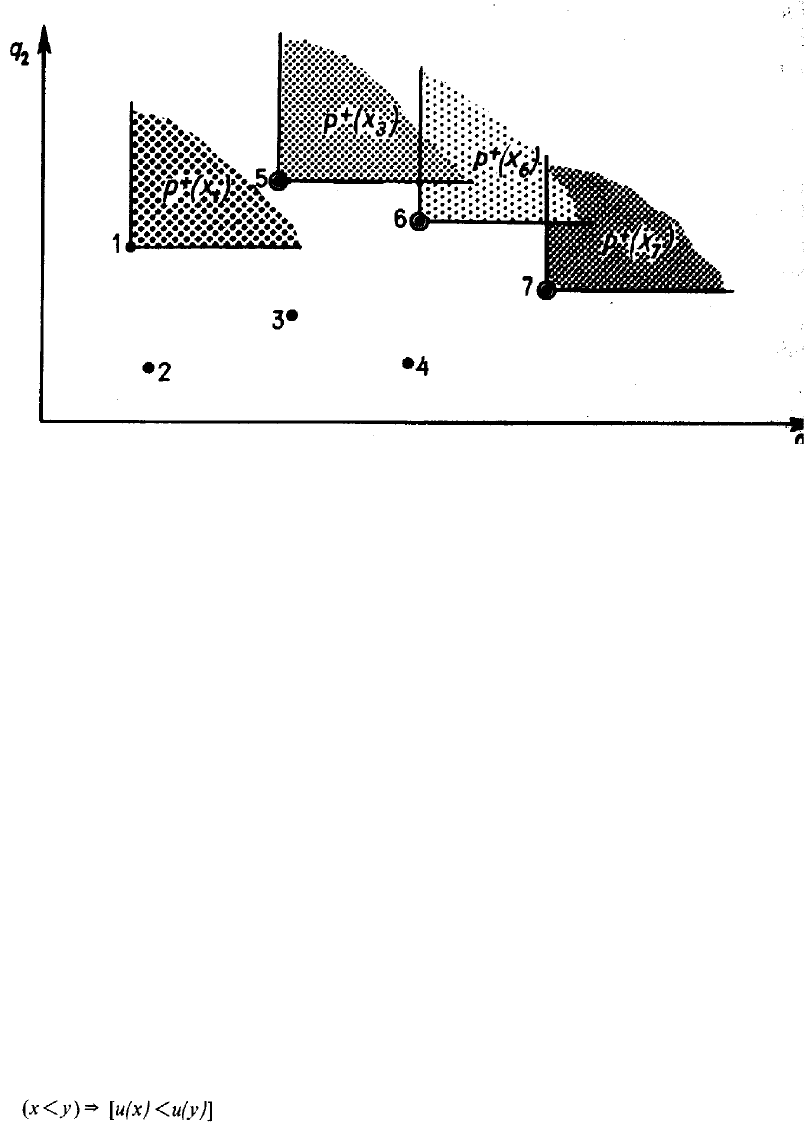
Рисунок 9.6.Описание паретовского множества как множества

таких альтернатив, для которых верхнее сечение Р+ (х) пусто

В общем же случае выделение наиболее предпочтительных

альтернатив возможно с помощью понятия оптимальности по

отношению, позволяющего придавать разный смысл понятию

"наилучший" (задавая разные отношения R). Элемент х  Х называется

мажорантой по отношению R на X, если для всех у  Х выполнено

условие y!Rx. Множество X

(R) всех мажорант называется

множеством R-оптимальных элементов.

Важно обсудить ситуацию, возникшую при описании выбора на

языке бинарных отношений в результате создания теории полезности.

П. Фишберн строго доказал теорему, смысл которой довольно ясен:

если множество Х конечно и между его элементами имеется

отношение строгого порядка, то можно построить такую вещественную

функцию и (х) на X, для которой

(в левой части < означает отношение предпочтения, в правой —

знак "меньше").

Функция и (х) называется функцией полезности. Ясно, что такая

функция не единственна: произвольное монотонное преобразование