Gulian A.M., Zharkov G.F. Nonequilibrium Electrons and Phonons in Superconductors

Подождите немного. Документ загружается.

SECTION 10.2. OSCILLATORY PROPERTIES OF A TUNNEL SOURCE 261

the source obtained in Ref. 10 and figuring in a number of papers (see Ref.

11) does not possess this property. The relevant expression

arises if one

drops in Eq. (10.7) all but the terms in the corresponding round

parentheses, drops also the terms

1,2

in (10.5) and (10.6), and then sets

Such a procedure may be justified only in the case of injection

in the range of directly above the gap, when the imbalance is insignifi-

cant. In the latter case, however, an interesting peculiarity of the tunnel

source resulting from the macroscopic phase coherence will be lost.

3. This peculiarity arises from the time-oscillating components

which are of a quantum nature (they vanish when

Since the solution of the nonlinear problem (10.13) yields the

which are explicitly time dependent, the entire

source (including the “stationary” generally “vibrates,” and the

Fourier spectrum of these oscillations (when the deviation from equilib-

rium is significant) cannot be represented by the first (Josephson) har-

monic only.

10.2.2. Oscillations of the Gauge-Invariant Potential

Thus if the electron injection in the NIS junction leads to the appearance of a

nonzero potential (see Sect. 8.1.1), in the SIS junction not only does the potential

appear, but having appeared, it should oscillate in time. At small these

oscillations would be of small amplitude near the stationary value and have the

Josephson frequency. We will now find certain quantitative characteristics of the

predicted effects.

Consider a symmetric SIS junction and use in calculations the collision integral

(4.119), accepting the electron–phonon collisions as the dominant relaxation

mechanism in (10.13). Assuming the deviation from equilibrium to be weak, we

present the difference in the form

Substituting (10.15) into (10.13) subject to (4.119) and (10.4), one obtains acoupled

system of integral equations for determination of

where the function is

262 CHAPTER 10. JOSEPHSON JUNCTIONS

while the operator is defined as

We also denoted here

where is the dimensionless electron–phonon interaction constant and is the

sound velocity.

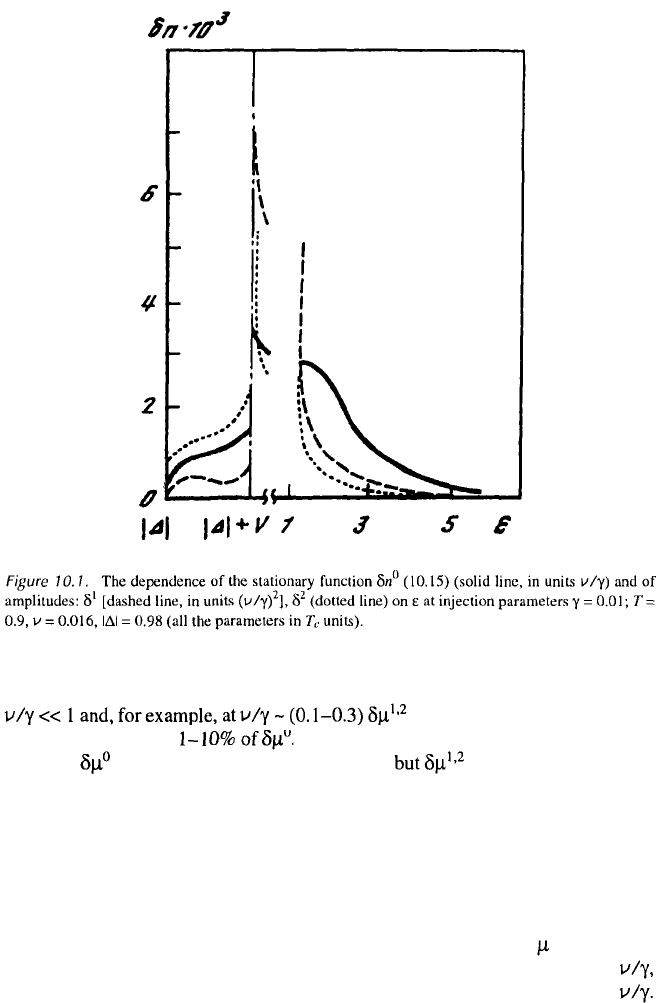
Obtaining results of the numerical solution of Eq. (10.16), shown in Fig. 10.1,

we may easily calculate the value of the gauge-invariant potential which

according to (8.6) equals

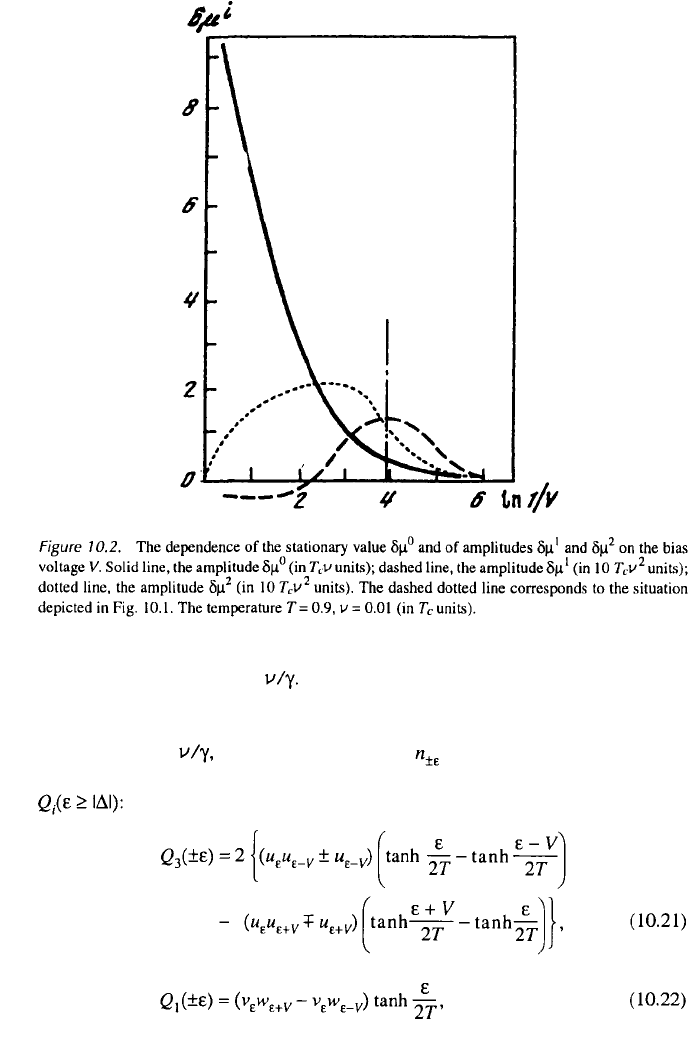
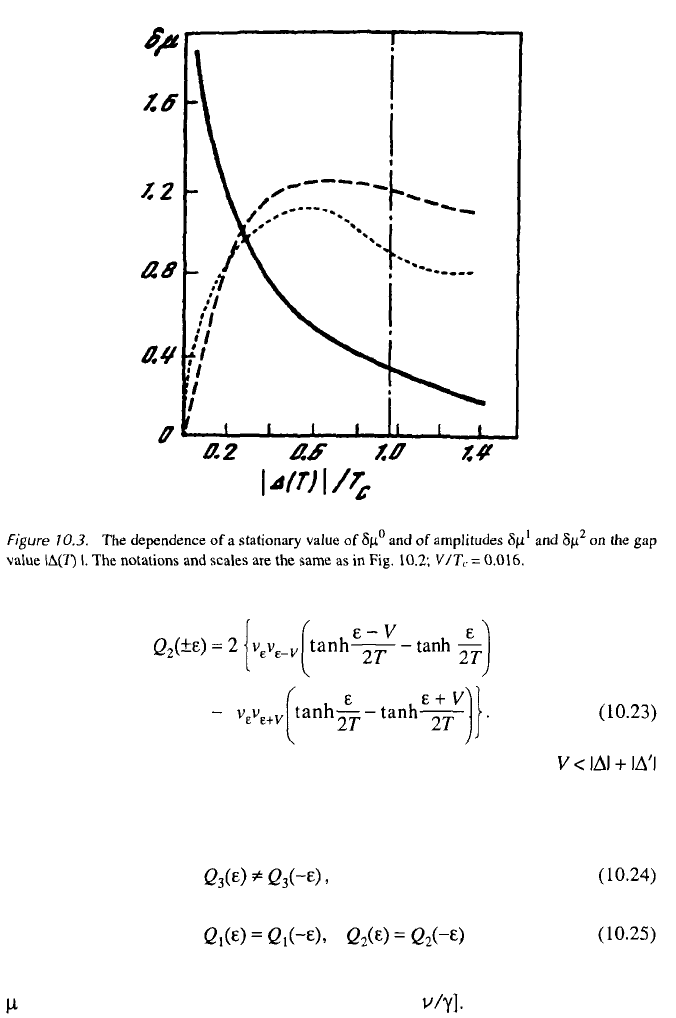
Figures 10.2 and 10.3 show the behavior of as the functions of V and T,

respectively. The stationary value of the junction, as an examination shows,

behaves analogously to that of the NIS junction. At sufficiently small values of v

(Fig. 10.2), the dependencies of are analogous to although with increasing

v the oscillations of reach a maximum and then diminish. At the same time,

the stationary part increases nearly without bounds (the only limitation is the

condition Another peculiarity of the oscillating terms in the potential

is their dependence on (i.e., on the temperature; Fig. 10.3). We have

Despite this, because of the

structural differences between [Eq. (10.4)].

SECTION 10.2. OSCILLATORY PROPERTIES OF A TUNNEL SOURCE 263

We should note that this examination, strictly speaking, is valid only when

may, as is clear from Figs. 10.2

and 10.3, account for In the most favorable cases the characteristic

values of may be on the order of a microvolt, may be fractions of this

value (say, tens or hundreds of nanovolts for low-resistance aluminum junctions).

Thus the oscillations of the nonequilibrium gauge-invariant potential may be

identified experimentally a detection scheme should be like in Fig. 10.4 with

voltmeter replaced by an oscilloscope.

10.2.3. Satellites in Scattered Radiation

The amplitude of oscillations of the gauge-invariant potential examined in

the previous section is of the second order of smallness in the parameter

whereas the potential itself (its time-averaged value) is a first-order effect in

The question arises of whether the oscillations of the tunnel source can appear in

264

CHAPTER 10. JOSEPHSON JUNCTIONS

the first approximation in Such an effect is described in the following

paragraphs.

We will focus on the kinetic equation (10.13). In the first approximation over

a small parameter

the distribution functions

in (10.4) to (10.7) may be taken

as equilibrium ones. As a result, one obtains the following expressions for

SECTION 10.2. OSCILLATORY PROPERTIES OF A TUNNEL SOURCE 265

In writing these expressions we have restricted ourselves to the case

(recall that the primed quantities and functions with shifted arguments correspond

to the injector). It is easily seen that the functions (10.21) to (10.23) have the

properties:

[The property (10.25) is responsible for the oscillating contribution to the potential

(10.20), being of the second order of smallness in From (10.25) it follows

that the oscillating nonequilibrium contributions to the distribution function of the

266

CHAPTER 10. JOSEPHSON JUNCTIONS

electron–hole excitations in the first order in are symmetric with respect to the

sign of We will find these contributions.

Consider the range of temperatures so that there is a sufficient

number of equilibrium electron excitations. The collision integral in (10.13)

may then be linearized in small deviations of the distribution function. The

stationary correction to in this case is determined by the term (10.21) and

yields an insignificant renormalization of The asymmetry with respect to

(property 10.24) causes an imbalance that we will also ignore in view of its

additional smallness (as follows from 10.21) and assume further that

Because the applied voltage

the variation

is localized at energies smaller

than T. This means that now we may use in (10.13) the relaxation time approxima-

tion for the collision integral (we postpone general discussion

of the validity of relaxation time approximation until Sect. 11.3):

where is a characteristic energy damping of the nonequilibrium excitations.

Substituting (10.21) to (10.23) and (10.26) into (10.13) and carrying out a Fourier

expansion of the nonequilibrium addition

SECTION 10.2. OSCILLATORY PROPERTIES OF A TUNNEL SOURCE 267

one obtains in the first order in the following amplitudes

where Using these expressions we may now consider the scattering of

external electromagnetic radiation by a nonequilibrium tunnel junction.

For a proper description of the scattering process, we must know the general-

ized of the nonequilibrium junction in response to the action of the

electromagnetic radiation. For this purpose we will use the photon–electron colli-

sion operator. The electron–photon collision operator was derived in the quantum

treatment of electromagnetic radiation in Sect. 5.3. Within the same lines one can

show that the desired photon–electron operator for “dirty” superconductors has the

form corresponds to the occupation number of photons with the frequency

268

CHAPTER 10. JOSEPHSON JUNCTIONS

where the prefactor n is proportional to the fine structure constant:

We have written the operator (10.30) in a general form that also accounts for

the branch imbalance. We are interested now in the classical limit of (10.30) when

In this case one can carry from under the integral signs (henceforth

we assume that is included in the prefactor n; we will not need the explicit form

of this factor and it will be omitted in the following discussion). Retaining only the

terms that correspond to the action of a field with frequency one obtains

where the functions [determined subject to (10.27) to (10.29)] acquire the form

(the contribution of in 10.15 is negligible),

SECTION 10.2. OSCILLATORY PROPERTIES OF A TUNNEL SOURCE 269

Before providing the results of the numerical analysis of these integrals, we briefly

comment on the physical picture.

According to (10.27) to (10.29), the density of electron excitations in thin

superconducting film oscillates with a small amplitude near its steady-state value owing

to the existence of macroscopic phase coherence in a system of single-electron

excitations. The interaction between the external electromagnetic radiation and the

oscillating electron density of states causes the scattering of the electromagnetic

wave with the formation of satellites at frequencies

The collision operator (10.30) allows one to calculate the response of the

nonequilibrium system, for example, to find the relative intensities of the satellites

in the reflected radiation. From the point of view of spectroscopic experiments,

however, it is easier to deal with the absorption coefficient of the system (specifi-

cally, with the imaginary part of the dielectric constant) or, in other words, with

characteristics of the wave that passes through the film.

Consider a test wave passing through one of the films of an equilibrium

superconducting junction. The absorption coefficient (up to a constant factor) is

given by formula (10.34). We assume that the oscillations of the type mentioned

earlier occur in the film. Then the absorption coefficient would also oscillate in

accordance with (10.33). As a result, the amplitude of the transmitting wave would

be modulated (we assume that and the satellites would appear. The

estimate of their relative intensity is as follows:

The presence of a second film in the junction, in which oscillations also occur,

somewhat distorts this simple picture. We will return to this question later.

Consider now the results of the numerical analysis of the junction’s behavior.

The function was calculated for three metals: lead,

niobium, and tantalum with the parameters shown in Table 10.1 (the data for

aluminum will be used later, in further considerations).

The growth of P with a drop in temperature (Fig. 10.5) is due to the reduction

in the number of equilibrium excitations, which makes the film effectively more

transparent [for convenience Fig. 10.5 shows the dependence in the BCS

*The value of was introduced in calculations as a cutoff factor to remove divergence at the integration

over in (10.35).

270 CHAPTER 10. JOSEPHSON JUNCTIONS

model]. One may become sure of that by direct analysis of the behavior of the

amplitudes (see the dotted lines in Fig. 10.5).

The presence of a (logarithmic) maximum near (Fig. 10.6) is a charac-

teristic feature of the dependence of P on the voltage V across the junction.

Corresponding voltages are optimal for detection of satellites.