Gross R., Sidorenko A., Tagirov L. Nanoscale Devices

Подождите немного. Документ загружается.

Thermoelectricity of Low-Dimensional Nanostructured Materials 295

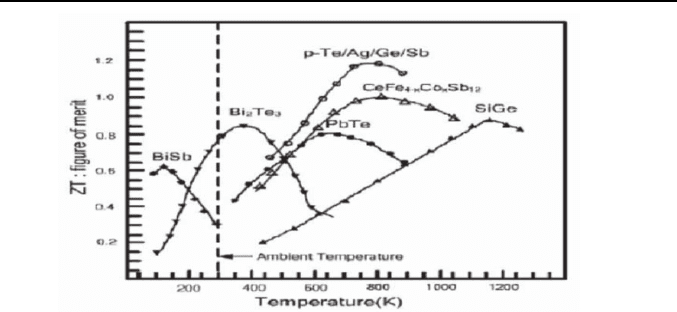
The best room temperature cooling bulk materials available at present are

alloys of Bi

with Sb

such as Bi

0.5

1.5

, p-type, and Bi

with

such as Bi

2.7

0.3

Thus the major objective in thermoelectric materials engineering and

investigation is to increase the figure of merit ZT =

×T/K, i.e. to

increase electrical conductivity σ and thermoelectric power S, and to reduce

thermal conductivity K.

Basis of Improved Thermoelectric Efficiency in

Nanostructured Materials

Recently, thermoelectric materials research experienced a resurgence

inspired by the development of new concepts and principles to engineer

thermoelectric transport in low dimensional nanostructures. Extensive

investigations of thermoelectric properties of low-dimensional structures

started in the 1990’s after a seminal paper [3] of Hicks and Dresselhaus. In

parallel the interests in certain bulk thermoelectric materials such as

skutterudites and others have been renewed. The general approach in

developing new thermoelectric materials and structures can be succinctly

summarized as engineering of electron and phonon transport. Solid-state

nanostructured materials are unique in offering the possibilities of tailoring

both the quantum-mechanical and transport characteristics of electrons and

phonons through the artificial structure potential landscape.

Fig. 1. ZT vs T for established thermoelectric materials.

, n-type, with typical ZT values close to one [2].

296 V. G. Kantser

Being quantum quasi-particles the motion of electrons and phonons in

nanostructured materials can develop in the range between two different

regimes: i) totally coherent motion (when electrons or phonons spreads in

the structure as waves); ii) totally incoherent motion (when either or both of

them spreads in the structure as classical particles). The regime of the

transport processes in the structures are determined by the correlation

between size-scale of the structure potential landscape and three physical

length scales of the quasi-particles: mean free path (MFP), phase breaking

length (PBL) and the Fermi wavelength (FWL). In the terms of electron

parameters high values of ZT request both high mobility and high density of

states. This can be realized in anisotropic materials or in multivaley

semiconductors with anisotropic carrier characteristics, when it is possible

to have a small effective mass in the current flow direction to give a high

mobility and large effective masses in the directions perpendicular to the

current flow to give a high density of states. Thus, in comparison with the

usual electronic transport in traditional low dimensional structures, the

thermoelectric structures involve the factor of carrier anisotropy. At the

same time such structures are characterized by several groups of carriers in

different energy valleys and the possibility of band pocket engineering

occur, which together with anisotropy offer a new opportunity to tailor the

thermoelectric transport. Hence the above mentioned length scales in

thermoelectric solid state structures based on anisotropic and multivalley

semiconductors (such as bismuth (Bi) like semimetals, IV-VI narrow gap

semiconductors, n-type Si and Ge) MFP, PBL and FWL of the carriers

become anisotropic. Therefore, in addition to the issue of thermoelectricity

such structures open new possibilities for the investigation of traditional

low dimensional transport effects in situations where several groups of

carriers with anisotropic physical characteristics are present.

In the regime of coherent motion due to quantum size effects in

nanostructured materials, such as quantum wells, superlattices, quantum

wires, and quantum dots, the energy spectra of electrons and phonons can

manipulated through the variation of the size of the structures. Such

low-dimensional nanostructures can be considered to be new materials [2],

when a new set of size parameters provides a “new” material. Since the

constituent

components of nanostructures are well known, the structures

are suitable to a certain degree of analysis, prediction and optimization.

When the quasi-particle motion is incoherent, it is still possible to utilize

classical

size effects to tailor the transport properties providing for

example a more effective scattering of phonons at the boundaries and

interfaces

than of the charge carriers. In the context of structure boundaries

Thermoelectricity of Low-Dimensional Nanostructured Materials 297

and interfaces classical size effects can manifest themselves for charge

carriers too, leading to a stronger energy dependence of the carrier time

relaxation.

Thus we can mention the following two physical approaches to improve

the thermoelectric efficiency of low dimensional nanostructured materials:

I. ZT enhancement due to quantum confinement of carriers

- energy states engineering

- carrier pocket engineering

- band structure anisotropy engineering

- concentration of electronic density of states near Fermi energy

- semimetal – semiconductor transition

- increasing of energy asymmetry of electronic density of states

II. ZT increase due to a decrease in the lattice thermal

conductivity by phonon engineering

- increased phonon – boundary scattering: thickness W

≤

phonon MFP

- reduced phonon group velocity due to phonon confinement effect in

2D and 1D structures: L ~ W << MFP

-phonon stop-band materials

The main aspects of the transformation of the density of states due to the

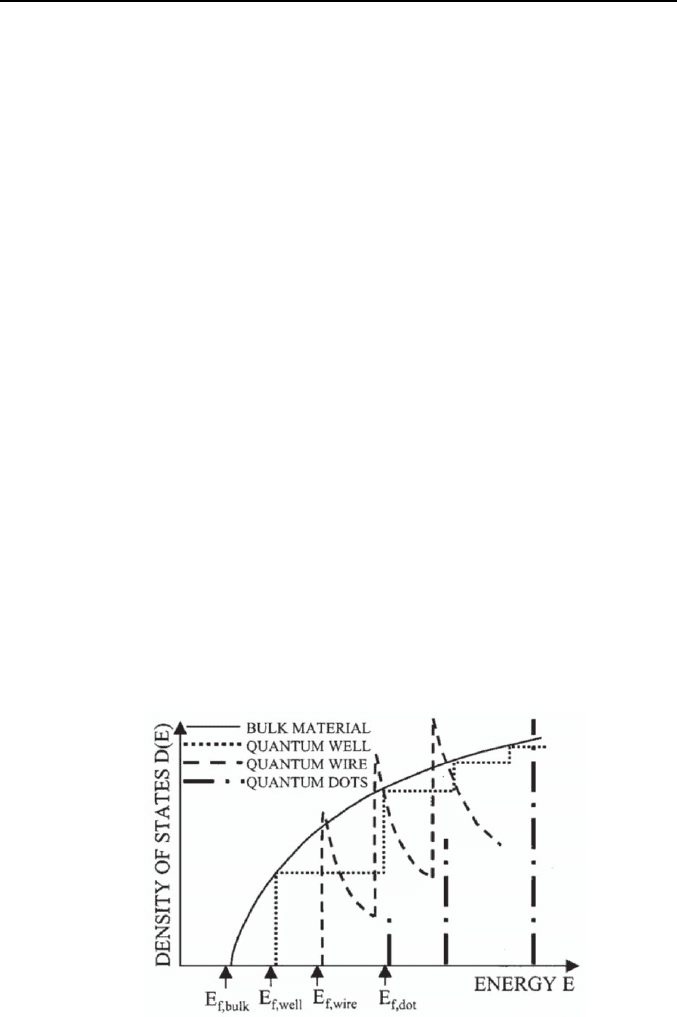
change in the dimensionality of the electron system are illustrated in Fig. 2.

Fig. 2. The density-of-states of electrons in systems of different dimensionality.

298 V. G. Kantser

Therefore it is challenging to develop new non-expensive methods of

fabrication of Bi

and PbTe thermoelectric elements as well as to

improve significantly its and others materials like bismuth thermoelectric

performance, in particular on the basis of approaches for the nanoscale

driven enhancement of thermoelectric properties.

Multiple Quantum Well and Superlattice Layered

Structures

The engineering of electron states in nanostructures in the direction to

improve thermoelectric efficiency have started with the consideration of a

layered systems with multiple quantum wells [3] analyzing the transport

parallel to the layers. A large number of theoretical and experimental

papers have demonstrated the enhancement of

ZT in the QW material of

n-type structures [4 - 7] due to electron confinement. Being one of the best

bulk thermoelectric materials lead telluride was among the first system

analyzed in the context of low dimensional thermoelectricity. The effect of

dimensionality on the power factor for n-type PbTe/PbEuTe Quantum Well

structures is shown in Fig. 4 on the basis of theoretical modeling [6, 7].

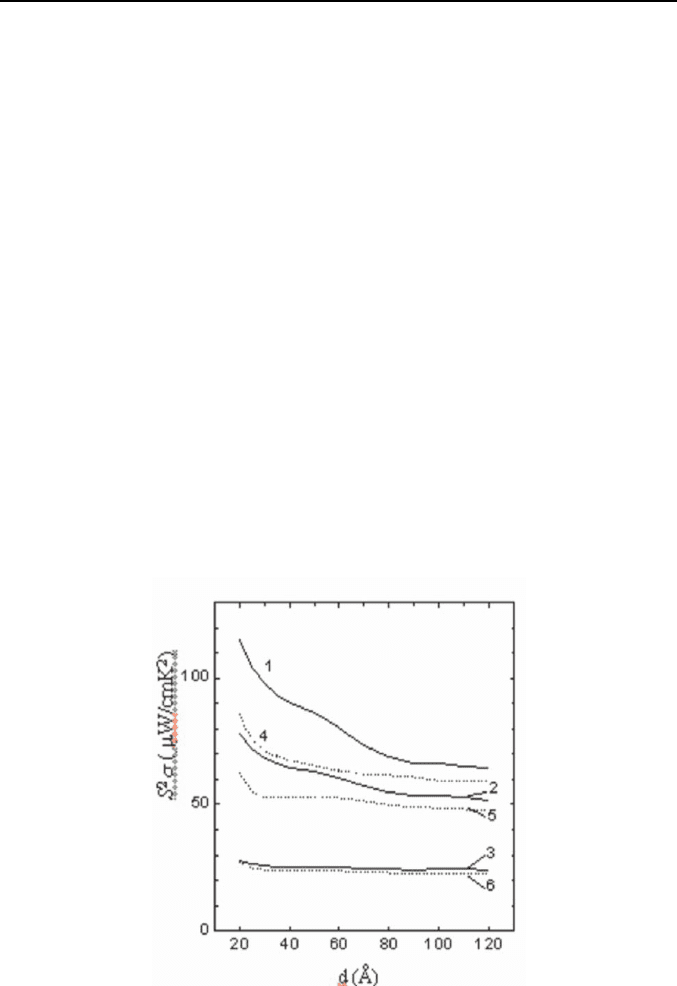
Fig. 3. Power factor for (100) and for (111) ones, (S

Φ)

111

(dashed lines) vs. well

width d at T = 300 K. Curves 1 and 4 are for n = 10

–3

; 2 and 5 for

n = 5·10

–3

; 3 and 6 for n = 10

–3

Thermoelectricity of Low-Dimensional Nanostructured Materials 299

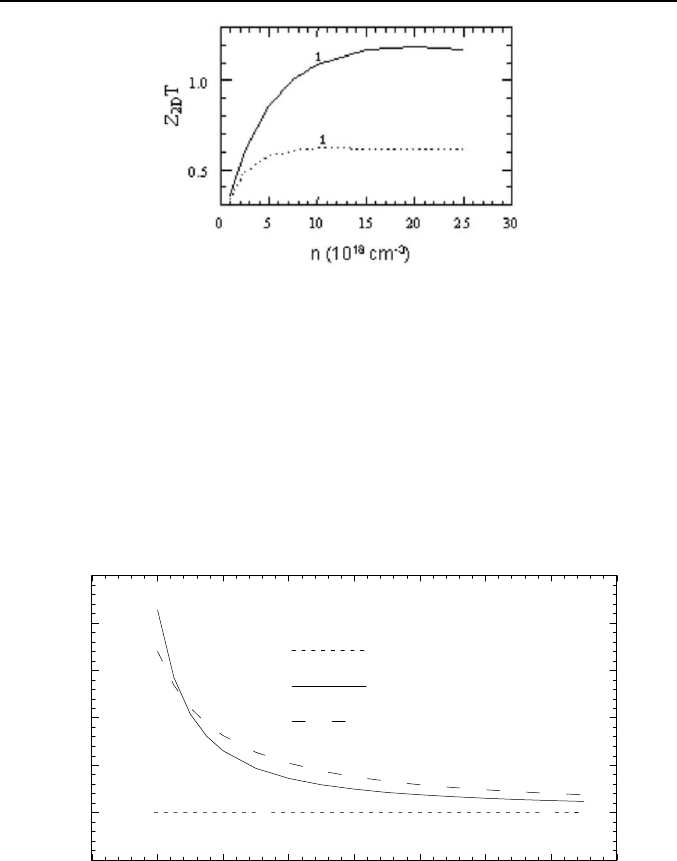
Fig. 4. Thermoelectric figure of merit Z

T of PbTe/Pb

1-x

Te as a function of

carrier concentration n for (100) oriented QWs (continuous curve 1) and for (111)

ones (dotted curve 1’). Potential barrier height U = 171 meV, x = 0.073, d = 2 nm,

T = 300 K (after [4]).

In p-type PbTe/PbEuTe quantum well structures the first experimental

demonstration of the principle of low dimensionality in thermoelectricity

obtained in [8] for p-type PbTe/PbEuTe quantum well structures can be

In the context of p-PbTe wells an other low dimensional approach have

been

reveal [9] it was suggested that quantum confinement will lead to the

Fig. 5. Thermoelectric figure of merit of p-type PbTe/Pb

0.927

0.073

Te quantum well

structures scaled by its bulk value as a function of well width d for two differen

scattering mechanisms (on acoustical phonons (DA) and optical phonons (LO)).

0 20406080100120140160

DA,

LO,

/ZT

d (Å)

U =

∞

U = 141 meV

U =

∞

was obtained. As an illustration in Fig. 5 the first experimental results

reproduced taking into account the finite weight of the barrier.

300 V. G. Kantser

change of the thermoelectric transport from L-type subbands to Σ -type

ones. The latter with higher density of states must be more favorable for the

improvement of thermoelectric properties. This is the case for PbTe where

we have 12 full valleys (energetic minimas) and 12 full ellipsoids of

constant energy in

Σ -points of the Brillouin zone. As a result, the density

of states must be higher and, respectively, the Seebeck coefficient and the

figure of merit must be higher too.

GeSi/Si QW structures are also materials utilized in bulk

thermoelectricity. The modeling of their thermoelectric properties and the

first experimental results indicate that the may have a higher possible figure

merit. It has been also shown that in such structures the phonon scattering

rate is considerably increased and, as a result, the QW in-plane lattice

thermal conductivity is strongly diminished [10]. For the optimization of

the thermoelectric properties of QW structures it is very important to take

into account the prospects of phonon engineering as well [2].ZA lot of

investigations so far has focused on the thermoelectric transport

perpendicular to the layer plane of structures. There are several aspects

related to the study the transport perpendicular to superlattice layer plane

[2]: i) tailoring the density of states using quantum size effects; ii) energy

filtering through thermionic transport; iii) reducing thermal conductivity by

stopping the propagation of some phonon modes; iv) selective scattering of

carriers with high and low energy.

The results obtained with the 1 nm / 5 nm Bi

/Sb

p-type

superlattices indicate that the phonon and charge carriers transport can be

tuned to improve ZT [11] by the so-called phonon-blocking/electron-

transmitting mechanism [12]. In the same paper encouraging results have

been also obtained with n-type 1 nm / 5 nm Bi

/Bi

2.83

0.17

n-type

superlattices, indicating ZT values higher than one at 300 K. The reason for

the less-than impressive ZT value of 1.46 at 300 K in n-type

/Bi

2.83

0.17

superlattices, compared to 2.4 at 300 K in the best p-

type Bi

/Sb

superlattices, is their higher thermal conductivity K.

Thermoelectric Wire Nanostructures

General theoretical considerations suggest that, because of their increased

quantum confinement effects, one-dimensional quantum wires could have

even larger enhancement in ZT. However, even without quantum

Thermoelectricity of Low-Dimensional Nanostructured Materials 301

confinement effects microwires are of significant importance due to the

following aspects:

(1) the one-dimensional shape of the microwire should be favourable

for

some synthetic textures;

(2) microwires may be convenient for some tiny-dimensional

applications such as natural “thermoelectric wires” taking

advantage of their characteristic shape.

Several mechanisms are combined to enhance ZT in nanowire arrays:

1. strong carrier quantum confinement in each quantum wire resulting

in a δ-function like density of states

2. suppression of phonon scattering

3. strong asymmetry of the energy dependence of the DOS.

Due to the very small effective mass of the charge carriers in Bi and

PbTe-like semiconductors, the effects of reduced dimensionality can be

seen in samples with dimensions of the order of 10 to 50 nm. In addition, it

was shown recently [13] that due to the anisotropy of the electron (hole)

energy ellipsoids, the quantum size effects in cylindrical Bi- like wires are

strongly enhanced. The origin of this effect is related to the peculiarities

arising from the wave propagation of anisotropic carriers - like caustics in

the geometrical optics of light propagation in ellipsoidal resonators.

Recently, the methods and corresponding technological equipment for

the fabrication of an array of Bi nanowires have been developed. Arrays

with wire diameters of 5-200 nm have been obtained by liquid-phase

pressure injection [14], vapour-phase deposition [15] and electrochemical

deposition [16]. Various transport investigations have been carried out to

highlight classical and quantum size effects [17-19]. As a host template

materials porous anodic alumina has been used and even single crystalline

nanowires of two orientations (normal to the (202) and (012) lattice planes)

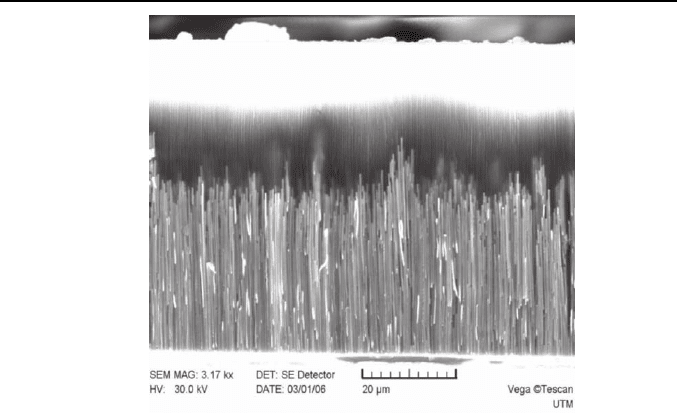
were fabricated. Figure 6 shows an image of an anodized alumina template

which is filled with bismuth by electrochemical deposition.

302 V. G. Kantser

Fig. 6. SEM image of Bi nanowire arrays in the alumina template. The wire

diameter is ~ 100 nm.

However, regarding the compatibility of the nanowire array technology

with the conventional technology of micro- and optoelectronic materials

and from the perspective of wire orientations and their doping the nanowire

array fabrication in porous silicon and III-V semiconductors seems to be

more attractive. Investigations in this direction started recently.

Nanowire arrays based on Bi are the most promising systems for re-

engineering the transport properties by making use of the quantum

confinement effect of the anisotropic carriers and size-induced semimetal-

semiconductor phase transitions, which are expected to result in good

parameters for thermoelectric applications [19]. In particular, the anisotropy

of the carrier pockets in Bi is outlined to be one of the key elements for

achieving significantly improved thermoelectric parameters. On the basis of

theoretical investigations, the thermoelectric figure of merit Z

T of Bi

nanowires is expected to increase significantly [19, 20] However, the

measurements of the thermoelectric properties (such as the Seebeck

coefficient and the thermal conductivity as well as a quantitative

explanation of these measurements (and even of existing results on

electrophysical investigations) are more challenging. Only recently, the first

results of the Seebeck coefficient measurements in Bi-wires

nanocomposites have been obtained [21]. The thermoelectric power was

found to increase considerable in Bi-nanowires with diameters less than

10 nm in alumina matrices.

the other hand the investigations of the Electric Field Effect (EFE)

on thermoelectric transport in solid state structures have been started

Thermoelectricity of Low-Dimensional Nanostructured Materials 303

recently [22]. In the context of nanowire structures the first theoretical

analysis show that thermoelectric transport and figure of merit can be

engineered by radial EFE [23]. For coaxial cylindrical capacitor

configuration of PbTe and Bi

nanowire structures was established that

the existence of the transition bipolar-monopolar semiconductor in radial

electric field, differences in carrier masses and mobility can essentially

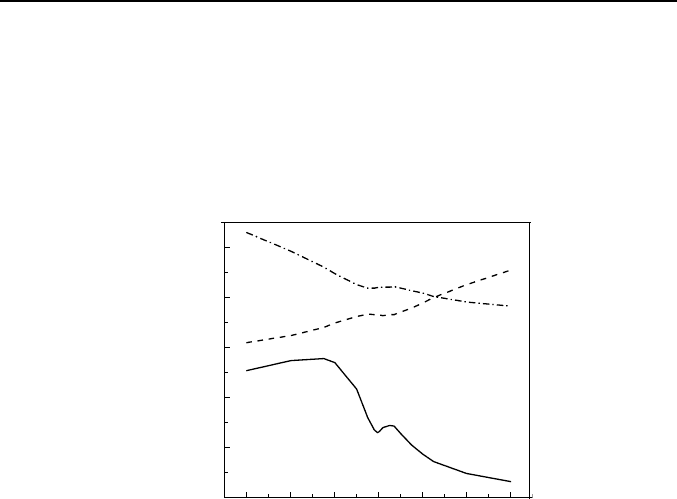
Fig. 7. Dependence of the Seebeck coefficient for electrons Sn (dash line), holes Sp

(dash dot line) and bipolar Seebeck coefficient S (solid line) on the gate voltage

cylindrical capacitor Bi

nanowire structures with diameter of 100 nm.

Quantum Dots and Three-Dimensional Nanostructured

Thermoelectric Systems

The most significant improvement of the thermoelectric figure of merit ZT

can be achieved by strongly reducing of the lattice thermal conductivity.

The

effect of phonon confinement on the lattice thermal conductivity in

low-dimensional structures is frequently treated in terms of additional

boundary scattering and the decrease of the phonon mean free path.

However, there is also another approach. When the phonon modes in the

confined structures are modified significantly, the group velocity of these

phonons usually decreases and this can strongly influences ZT [22]. Due to

the specific properties of quantum dot systems both implications of size

-300 -200 -100 0 100 200 300

100

200

300

400

500

Seebeck coefficient [

µV/K]

Gate voltage [V]

modified the thermoelectric properties (Fig. 7).

304 V. G. Kantser

effects – classical and quantum – on the characteristics of the phonon

system and the thermal conductivity have been intensively studied over the

last years [24]. In such approach quantum dot systems represent an example

of the abovementioned ‘phonon-blocking electron-transmitting’ [12]

structure with a great potential for thermoelectric applications.

An illustrative result of numerical calculations for a structure that consists

of multiple layers of Si with array of Ge quantum dots separated by wetting

layers and spacers are shown in Fig. 8.

Fig. 8. Figure of merit ZT of Si/Ge quantum dot systems scaled by its bulk value

(ZTexp(Si)=0.05 - 0.06 at 300 K) as a function of Fermi energy for two different

value of thermal conductivity (15 W m

–1

and 156 W m

–1

respectively).

There the electron and phonon transport modifications due to the space

confinement caused by the mismatch in electronic and thermal properties

between dot and host materials have been taken into account. The analysis

shows that the enhancement of the thermoelectric figure of merit ZT is

mostly due to the significant drop in the lattice thermal conductivity caused

by the acoustic phonon scattering by quantum dots.

take advantage of both the superlattices and the nanowires to design

a better thermoelectric system in [26] another variant of nanostructured

quantum dot like systems have been proposed and investigated. The

electronic density of states and the thermoelectric properties of superlattice

nanowires made of various lead salts (PbS, PbSe, and PbTe) have been

investigated as a function of the segment length, wire diameter, crystal

orientation along the wire axis, and the length ratio of the constituent

-3

-2

-1

-0

-0.1-0.2

0.1 0.2

-0.3

Fermi Energy (eV)

/ZT

Gross R., Sidorenko A., Tagirov L. Nanoscale Devices - Fundamentals and Applications

Подождите немного. Документ загружается.