Gross R., Sidorenko A., Tagirov L. Nanoscale Devices

Подождите немного. Документ загружается.

252 S. L. Prischepa

It is reasonably to suppose that the same research program should be also

realized for S/X multilayered structures (X denotes the non

superconducting material). Until recently, the obtained theoretical results

for multilayers have been mostly related to the temperature and angular

dependencies of the second upper critical magnetic field, H

(Θ,T) [7, 8].

At the same time the results of experimental measurements of H

(Θ,T)

dependencies differ from theoretical models [9,10] which, however, mostly

consider infinite stacks of S and X layers [7]. For example, at present the

effect of the surface critical magnetic field, H

, on the multilayered

structures is not well understood. Firstly, the definition of H

for S/X

samples is not known and secondly it is not clear how to calculate this

quantity for multilayers. Furthermore, it is not well known in which cases

the S/X structure could be considered as (i) infinite, (ii) semi-infinite

medium or as (iii) sample with two boundaries. The criterion, at least

empirical, for these definitions, is absent in the literature.

For these reasons we decided to perform a series of experiments in order

to study the influence of finite dimensions on the thermodynamic quantity

of S/X multilayers as well as its temperature and angular dependencies.

We choose X=N, where N stands for a normal (non superconducting)

metal. This means that the proximity effect is responsible for the coupling

between the different S layers. At this initial stage of our research we

restrict ourselves to the two simplest cases: (i) the symmetry plane of the

multilayer falls into the center of the superconducting layer and (ii) the

symmetry plane falls into the center of the normal layer.

In this work we present results of the experimental investigation of (i) the

temperature dependence of the upper critical magnetic field paying special

attention to the configuration with the applied magnetic field parallel to the

film surface and (ii) the angular dependence of the upper critical magnetic

field at different temperatures. Both kinds of experiments were performed

for samples with the symmetry plane in S or in N layers.

We have studied the properties of both Nb/Cu and Nb/Pd multilayers.

The choice of Nb for the fabrication of the superconducting multilayers was

related to the fact that it has the highest critical temperature among the

superconducting elements. The choice of Cu was motivated by the

possibility of creating the Nb/Cu multilayers with high quality structural

properties [11]. Moreover, the proximity effect is very well studied in this

system [12]. On the other hand, we choose Pd because among the normal

metals

it turns out to be particularly interesting. It is in fact characterized

by a large value of the spin susceptibility and in some alloys (i.e. Pd

1-x

) ferromagnetic behavior is obtained even for small values of x

[13]. Moreover, the interface of the Nb/Pd system is more transparent

compared to the Nb/Cu system [14]. These differences between the two

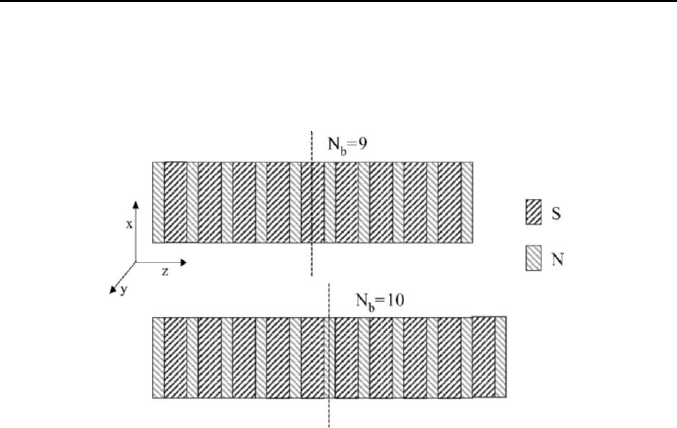
Properties of S/N Multilayers with Different Geometrical Symmetry 253

studied systems give us the opportunity to generalize the observed

symmetry effect to the class of the proximity coupled metallic multilayers.

Fig. 1. The geometrical configuration of the Nb/Pd samples for N

=9 and N

=10.

For all investigated samples the top and the bottom layers consist of the

normal metal. In this way, taking into account the constant period of the

multilayer, the central layer is superconducting in the case of an odd

number of bilayers (N

) and normal for an even N

. This means that for odd

(even) N

values, taking into account the capping N layer, the symmetry

plane of the whole sample falls into the center of the S (N) layer (see Fig.

1). The thickness d

of the S layers is always 200Å for both compositions.

In Nb/Pd samples, the thickness d

of the Pd layers is equal to 100Å. In

fact, as has been shown recently, the presence of a 100Å thick Pd layer

results in a temperature induced dimensional crossover in the Nb/Pd

systems [15]. When the Pd layer thickness increases towards 200Å, the

system behaves as 2D in the whole temperature range [15]. For the Nb/Cu

system we chose d

= d

= 200Å. In fact, for these values a pronounced 2D-

3D crossover is usually observed on increasing temperature at a crossover

temperature T* [12]. We show that changing the number of bilayers, i.e.

changing the symmetry of the samples, a drastic change in the

dimensionality of the system occurs for T→T

, with a 2D behavior observed

almost up to T

for samples in which the symmetry plane lies in the center

of the S layer.

Also we show that, as it was mentioned in [12], the global angular

dependence of the H

for S/N layered superconductors is much more

complicated than for isolated films [5,16]. Moreover, the measured

(T, Θ = 0) and the H

(Θ) dependencies do not correlate to each other

254 S. L. Prischepa

with the H

(Θ) dependences being more sensitive to the nucleation

character of the superconducting phase.

Sample Preparation and Experimental Details

Pairs of Nb/Pd and Nb/Cu samples with N

= 9 and 10 were grown on

Si(100) substrates at room temperature by using a dual source magnetically

enhanced dc triode sputtering system [15]. The deposition rates were 9 Å/s

for Nb, 8 Å/s for Pd and 5 Å/s for Cu. Nb/Cu samples were deposited in

different deposition runs, while Nb/Pd samples were sputtered

simultaneously. A specially designed movable shutter allowed the

simultaneous deposition of the two samples with different number of

bilayers. The starting position of the sample holder was located between the

Pd and Nb guns and two substrates were mounted on it. N

+1 bilayers were

deposited on the substrate positioned closest to the Pd target, while N

bilayers were deposited on the other substrate. The platform where the

samples are mounted can be rotated in a controlled way over 360 degrees

using a stepper motor to reach every position. At the beginning of the

process the sample holder is sent to the Pd gun to sputter the first layer (the

two samples will consist of N

or N

+1 Nb/Pd bilayers plus a bottom Pd

layer). Then, after Pd deposition, the sample holder is moved, through the

zero position, to the Nb gun. This movement from the Nb to the Pd gun is

repeated alternately until on both samples N

bilayers plus the Pd bottom

layer have been sputtered. Then, the sample holder is moved from the Pd to

the Nb gun in the direction opposite to the zero position to sputter the Nb

layer only on one sample. The sample holder has a diameter of 2.5 cm and

the distance between the two substrates is almost 2 cm. This allows us to

use a shutter close the Nb gun to prevent Nb deposition also on another

sample during this last Nb deposition step. After this, the sample holder is

slightly moved back and the Nb gun is switched off. When we are sure that

the Nb rate is zero (usual waiting time is 1 minute), the sample holder is

moved, through the Nb gun, to the zero position, and finally to the Pd gun

to sputter the last Pd layer only on this second sample. This last step is

possible due to the presence of another shutter close the Pd gun. Finally the

sample holder is moved back to the zero position and the deposition process

is completed.

X-ray reflectivity measurements confirmed the layered structure of the

samples with an interface roughness of the order of 10 Å [15]. Transport

measurements with a standard four probe technique were performed for

both

parallel and perpendicular magnetic field orientations. The resistance

Properties of S/N Multilayers with Different Geometrical Symmetry 255

was measured with the accuracy of 10

-4

Ohm, while the measured accuracy

of the magnetic field was 10

-4

T. The samples from each pair were

simultaneously mounted in an insert with the possibility to rotate them in

the liquid helium bath. The accuracy of the rotation angle was ± 0.1°. The

value Θ = 0 corresponds to the magnetic field direction parallel to the film

surface. A superconducting Nb-Ti solenoid with T

= 7.2 K was used to

produce the external magnetic field. The H

values were extracted from the

R(H) curves measured at the onset of the superconducting transition. The

temperature stabilization during the measurements was ± 0.01 K. The

transition widths ∆T

in zero magnetic field were always less than 20 mK,

while at parallel fields higher than 2 Tesla their values were less than

300 mK, confirming the high quality of the samples. From H

c2⊥

(T) curves

we have calculated the values of ξ

(0) which was of the order of 120 Å for

all samples. We named the samples using the letter S or N according to

whether the symmetry plane lies in the center of S or in the center of N

layers, respectively, followed by a letter that indicates the normal metal

used (P for Palladium and C for Copper). For example, SP is the Nb/Pd

multilayer whose symmetry plane lies in the S layer (N

=9) while NC is the

Nb/Cu sample with the symmetry plane in the center of the N layer

=10).

The deposition of the Nb/Pd multilayers in the same run allows us to

consider the same Nb as well as the same interface properties in each

sample [17]. This hypothesis is confirmed by the fact that for these two

samples the same values have been obtained for the resistivity

∼ 9 µΩ×cm, the residual resistivity ratio β

≈ 1.6 and the coherence

length ξ

(0) ≈ 125 Å. The macroscopic parameters of Nb/Cu samples were

also very similar. Therefore, we believe that the only difference between

each pair of samples is in their symmetry due to their different finite

dimensions.

The choice of 9 and 10 number of bilayers for the samples studied in this

work was based on the result of our previous research [17]. In ref. 17 the

effect of the symmetry on the resistive characteristics of Nb/Cu multilayers

prepared in the same way as in this work was investigated for N

in the

range 5…12. It was shown that for N

> 10 the symmetry effect becomes

less pronounced due to the smaller influence of the surface effects with

increasing the N

value. In order to demonstrate the validity of the observed

phenomena we have also prepared another pair of Nb/Cu samples with N

equal to 5 and 6. This couple of multilayers have been fabricated in the

same deposition run.

256 S. L. Prischepa

Temperature Dependence of the Upper Critical Magnetic

Field

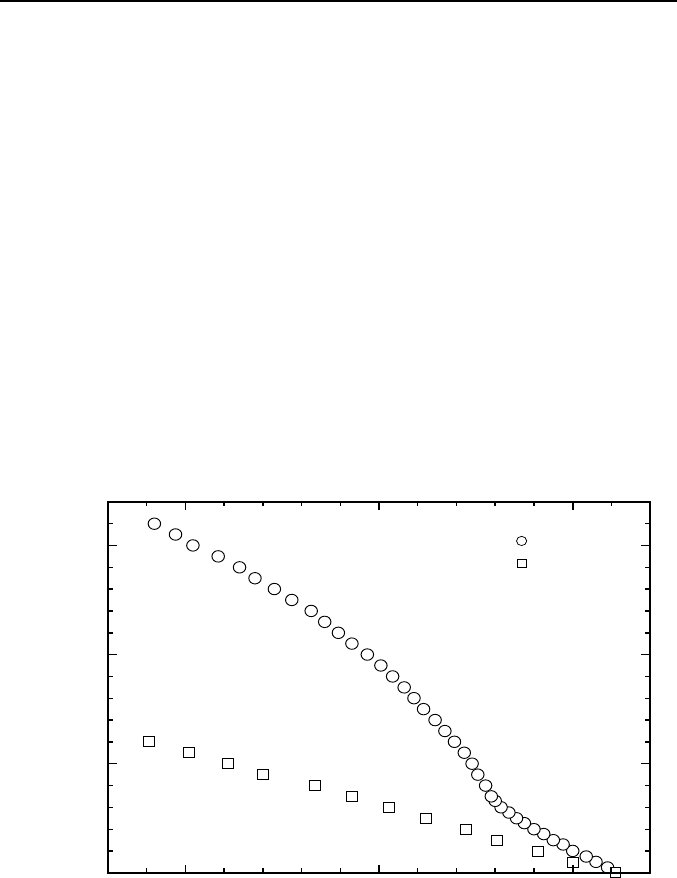
In Fig. 2a we present the measured temperature dependencies of parallel

and perpendicular magnetic fields for the sample NP. The behavior of

c2||

(T) reveals the conventional 2D-3D crossover for S/N multilayers

[7, 9, 10, 12, 15, 18].

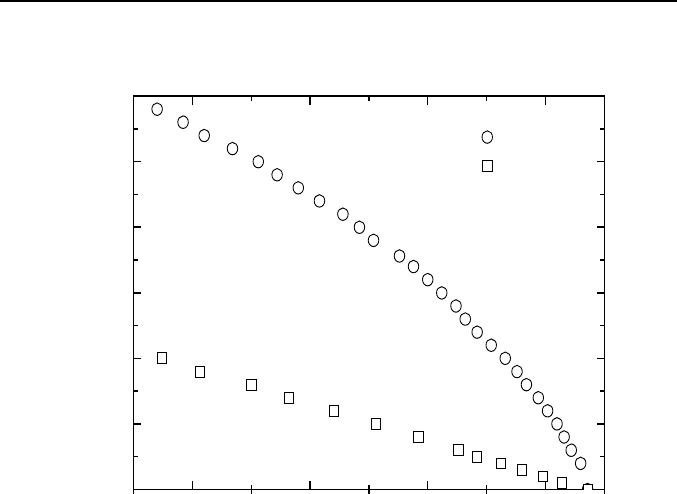
In Fig. 2b we present the H-T phase diagram for sample SP, with the

symmetry plane in the center of the Nb layer. It is clearly seen that the

c2||

(T) curve is quite different, while the H

c2⊥

(T) dependence is very similar

to that of NP sample. We did not see the pronounced linear part in the

c2||

(T) dependence as it is usually observed for S/N multilayers in the case

of d

≈ d

≈ ξ

. The H

c2||

(T) curve seems to be square root like in the whole

temperature range even close to T

. This is the signature of the 2D behavior.

234

(T)

T(K)

C2||

C2perp

Fig. 2a. H-T phase diagram for sample NP.

Properties of S/N Multilayers with Different Geometrical Symmetry 257

2,02,53,03,5

0,0

0,5

1,0

1,5

2,0

2,5

3,0

C2| |

C2perp

(T)

T(K)

Fig. 2b. H-T phase diagram for sample SP.

As already pointed out, both the samples SP and NP were obtained in the

same deposition run and therefore represent the same Nb properties and

Nb/Pd interface behaviors. The only difference between these two samples

is the different number of bilayers and, consequently, their different

symmetry. To confirm the effect of the samples’ symmetry on the H

c2||

(T)

dependencies

have

investigated another S/N system. We have

fabricated and measured a pair of multilayers with a different N material,

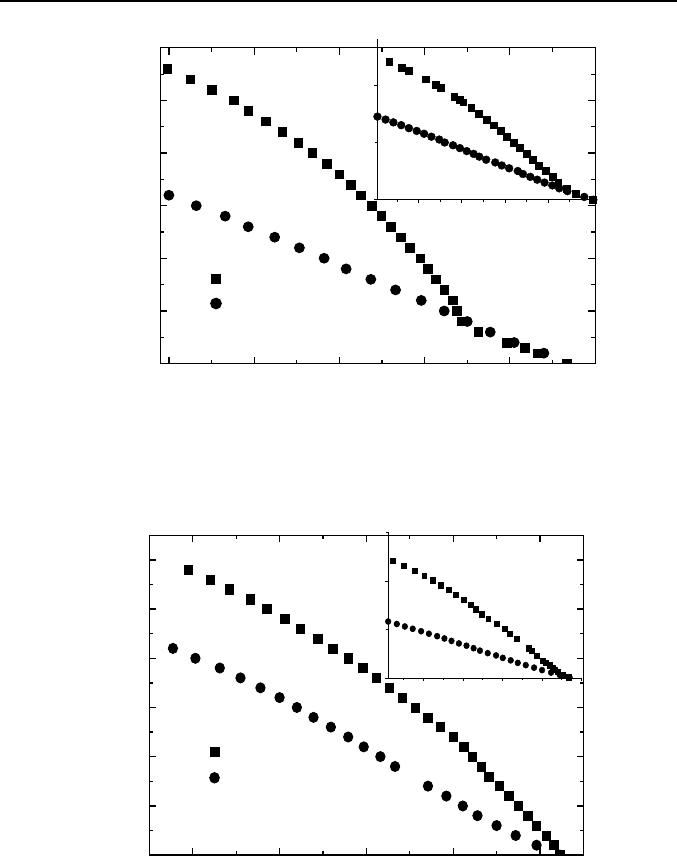
namely Nb/Cu, with 10 (NC sample) and 9 (SC sample) bilayers. Taking

into account the absence of the large spin susceptibility in Cu compared to

Pd [13],

the thickness of Cu was larger, d

= 200Å. The results of the

(T) measurements for the NC and SC samples are presented in Fig. 3a

and

Fig

3b,

respectively

[18].

Again

the

c2||

(T) dependence for the

sample NC is usual for the S/N multilayers revealing a pronounced 3D-2D

crossover. The H

c2||

(T) dependence for the sample SC is square root like in

the

whole

temperature

range

up to T

. In the inset of Fig. 3a we show the

H-T plot for the Nb/Cu multilayer with N

= 6. Furthermore, in the inset of

Fig. 3b the H-T phase diagram is presented for another Nb/Cu sample with

258 S. L. Prischepa

234567

0,0

0,5

1,0

1,5

2,0

2,5

3,0

c2||

c2perp

(T)

T(K)

34567

(T)

T(K)

Fig. 3a. H-T phase diagram for sample NC. Inset: the same for sample with N

=6.

23456

0,0

0,5

1,0

1,5

2,0

2,5

3,0

c2||

c2perp

(T)

T(K)

34567

(T)

T(K)

Fig. 3b. H-T phase diagram for sample SC. Inset: the same for sample with N

=5.

= 5. Also in this case the behavior of H

c2||

versus T depends almost only

on the symmetry of the multilayers.

Based on the obtained results for different systems and a different

number of bilayers, we may conclude that the observed increase of the

temperature interval of the 2D nature of samples with the symmetry plane

Properties of S/N Multilayers with Different Geometrical Symmetry 259

in the center of S layer is a general feature of S/N metallic multilayers.

According to our opinion, this behavior is mainly due to the effect of finite

dimensions on the nucleation of superconductivity. In order to get deeper

insight into the problem, we performed angular measurements of the upper

critical magnetic field for Nb/Pd and Nb/Cu samples at different

temperatures.

Angular Dependence of the Upper Critical Magnetic Field

In this section we will present the angular dependences of H

at different

temperatures. For sample SP we performed such kind of measurements in

the temperature interval 1.91 K ≤ T ≤ 3.61 K (0.52 ≤ t = T/T

≤ 0.98). The

results of the measurements for two temperatures (3.50 K and 1.91 K) are

presented in Fig. 4. As it is clearly seen, there is no significant difference in

the shape of the H

(Θ) curve for both temperatures. The dashed lines in

Fig. 4 correspond to Tinkham’s formula [5] for a 2D thin film. It is seen

that the theory explains well the H

(Θ) data, especially at small angles

(|Θ| < 20°). The present result is typical for this sample. The same behavior

was observed also at other temperatures as well as for Nb/Cu multilayers.

According to our opinion it confirms the 2D character of superconductivity

of S/N multilayer with an odd number of bilayers in the whole temperature

range.

-20-10 0 102030405060708090

1000

2000

3000

4000

5000

6000

10000

15000

20000

25000

30000

(Oe)

T=3.50K

T=1.91K

Fig. 4. H

(Θ) for sample SP at two temperatures. The dashed lines are for the

Tinkham result.

260 S. L. Prischepa

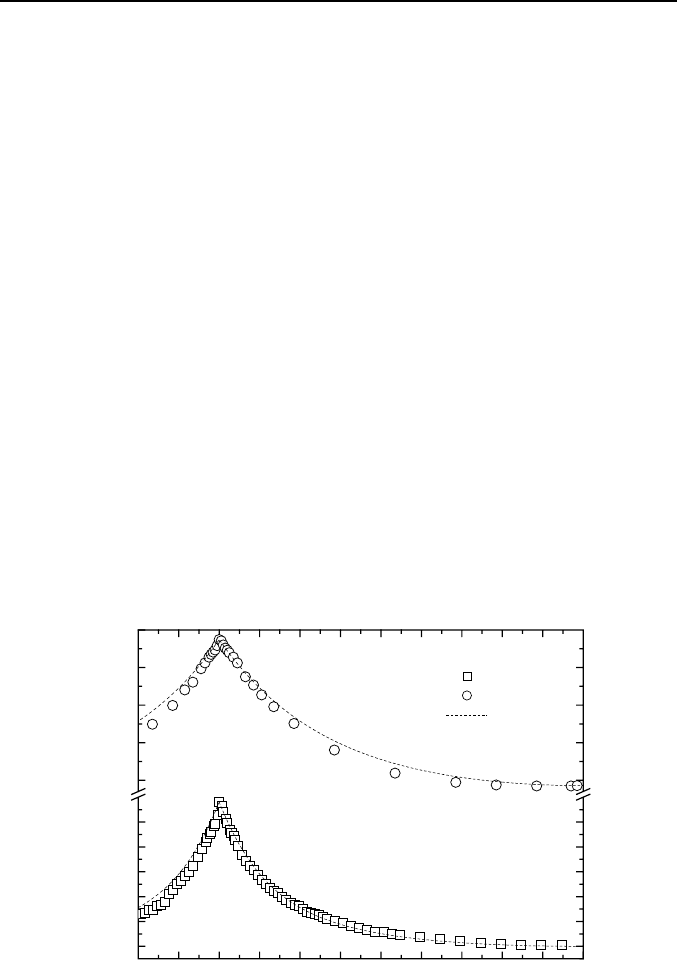
In Fig. 5 we show the H

(Θ) dependences for sample NP at 4 different

temperatures: T = 4.19 K (t = 0.99), T = 3.97 K (t = 0.94), T = 3.45 K

(t = 0.82), and T = 2.05 K (t = 0.49). As it is clearly seen, the shape of the

(Θ) curves changes significantly with temperature. At T very close to T

(t = 0.99), the features of 3D behavior is present and the curve is bell-

shaped. The solid line in this figure corresponds to the 3D Lawrence-

Doniach result [16].

100

200

300

400

500

600

700

800

-100 -80 -60 -40 -20 0 20 40 60 80 100

4000

6000

8000

10000

12000

14000

T=4.19K

(Oe)

1000

1250

1500

1750

2000

2250

2500

T=3.97K

T=3.45K

7500

12500

17500

22500

27500

T=2.05K

Fig. 5. H

(Θ) for sample NP at 4 temperatures. The dashed lines are for the

Tinkham result and the solid line is for the Lawrence-Doniach result.

Properties of S/N Multilayers with Different Geometrical Symmetry 261

Good agreement with the experiment is seen for |Θ| < 20°. This, indeed,

corresponds to the linear H

(T, Θ = 0) dependence. But at the slightly

smaller reduced temperature t = 0.94, at which H

(T, Θ = 0) is still a linear

function, the measured H

(Θ) curve reveals a pronounced cusp. This is in

disagreement with the dimensionality derived from the measurement of the

temperature dependence of the parallel upper critical magnetic field.

Moreover, the experimental data are well described by the thin film limit

[5] (dashed line for data of this temperature). In the region around T*

(t = 0.82) the H

(Θ) curve becomes more complicated showing a sudden

increase of the H

values at Θ < 10°. Finally, at low temperatures

(t = 0.49), the experimentally measured H

(Θ) dependence becomes

similar to the H

(Θ) dependence of a thin film, however, in the same way

as found previously for different multilayers [19], the experimental points

fall faster than the Tinkham curve (dashed line).

The results presented in this section show the different behavior of the

angular dependences of the upper critical field for two different kinds of

samples. For multilayers with the symmetry plane in the center of S layer,

the H

(Θ) curves are well described by the expression for 2D thin films,

for which the nucleation position of the superconducting phase is supposed

be in the center of the sample. Moreover, the two-dimensionality of

these

samples was also confirmed by the results of the H

(T)

measurements (Figs. 2b, 3b). From this point of view it is reasonable to

suppose that for this kind of sample there is only a single superconducting

nucleus at the H

value for the whole investigated temperature range in the

parallel

magnetic field configuration. Moreover, it is likely that this

nucleus is located in the middle of the central S layer. At the same time the

physical picture for samples with the symmetry plane in the central N layer

is more complicated. First of all, at T very close to T

, where the coherence

length

is larger than the sample dimensions, the H

(Θ) curve is bell-

shaped

with the derivative d H

(Θ)/d Θ |

Θ=0

=0. This reflects a 3D

behavior.

Then, still in the temperature region of 3D behavior (according

to the H

(T, Θ = 0) result), but at slightly smaller temperatures (t = 0.94),

the H

(Θ) curve has a cusp. Previously, the presence of a cusp in the

(Θ) curve was considered as a prove of two-dimensionality. Our

experimental results strongly indicate that for S/N multilayers this is not

always

the case. At least it is not valid for samples with the symmetry

plane within N layer. In the region of the 2D behavior (according to the

(T, Θ = 0) result), where the value of ξ becomes comparable to the

multilayer period, the H

(Θ) curves become more complicated revealing

the probable complex character of the superconducting phase nucleation in

these samples. The likely reason of such effects could be related to the

Gross R., Sidorenko A., Tagirov L. Nanoscale Devices - Fundamentals and Applications

Подождите немного. Документ загружается.