Громкович Ю. Теоретическая информатика. Введение в теорию автоматов, теорию вычислимости, теорию сложности, теорию алгоритмов, рандомизацию, теорию связи и криптографию
Подождите немного. Документ загружается.

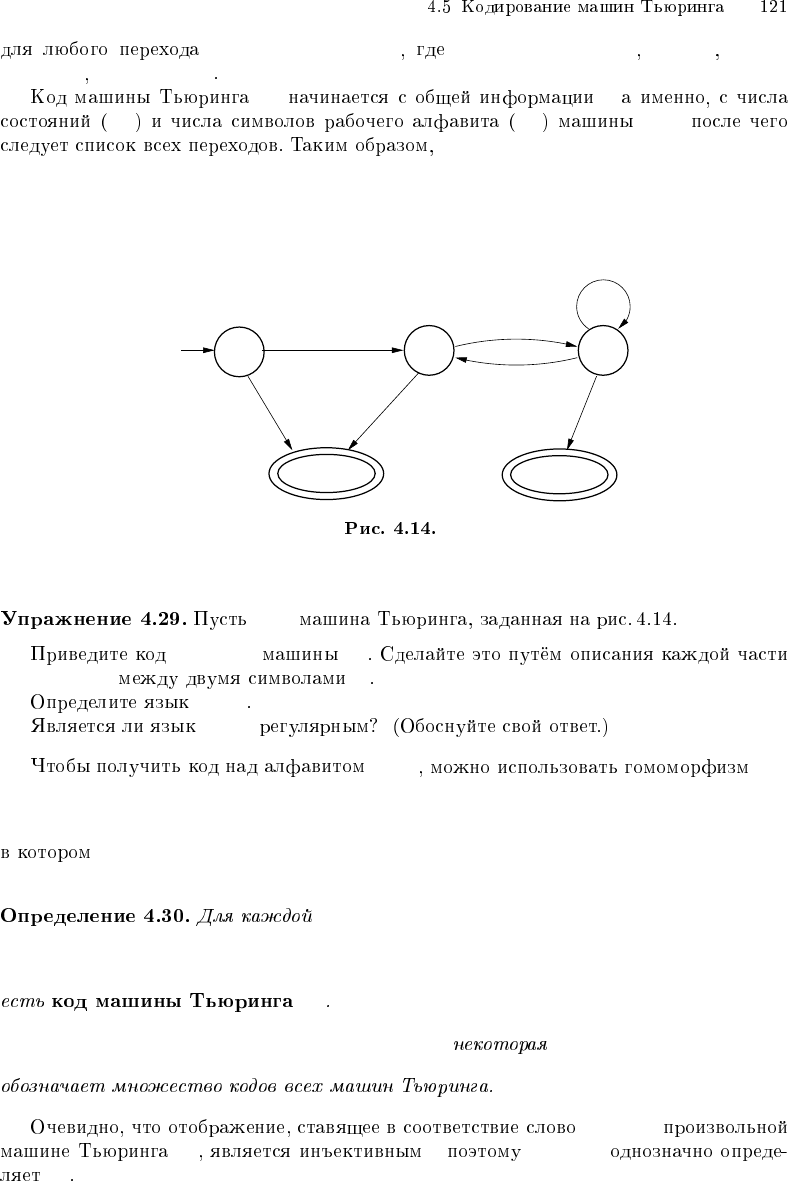
δ(p, A
l
) = (q, A
m
, α) p ∈ {q
0
, q
1
, . . . , q
m
} q ∈ Q l, m ∈
{1, . . . , r} α ∈ {N, L, R}
M
|Q| |Γ | M
Code(M) = #0
m+3
#0
r
##Co de(Transition
1
)#Code(Transition
2
)# . . . .
q
0
q
1
q
2
q
accept
q
reject
¢ → ¢, R
¢ → ¢, R
0 → 0, R
0 → 0, R
1 → 1, R
t
→
t
, L
a → a, N
b → b, N
a ∈ {0, 1,
t
}
b ∈ {1, ¢,
t
}
M
• Code(M) M
Code(M) #
• L(M)
• L(M)
Σ
bool
h : {0, 1, #}
∗
→ (Σ
bool
)
∗
,
h(#) = 01, h(0) = 00, h(1) = 11.
MT M
Kod(M ) = h(Co de(M ))
M
KodMT = {Kod(M) | M MT}
Kod(M)
M Kod(M)
M

Code(M)
M
x ∈ {0, 1}
∗
x ∈ KodMT x
A
ver
Σ
bool
KodMT x ∈ (Σ
bool
)
∗
x MT
x ∈ (Σ
bool
)
∗
i
x i MT
• x = Kod(M ) M
• {y ∈ (Σ
bool
)
∗
| y x
} i −1
x = Kod(M ) i MT M i
M
i
i MT M
i
i
i Kod(M
i
) Gen
IN (Σ
bool
)
∗
Gen(i) = Kod(M
i
)
Gen
Kod(M
i
)
i
Gen
i ∈ IN
x := 1; {x (Σ
bool
)
∗
}
I := 0;
I < i
A
ver
x ∈ KodMT
x ∈ KodMT
I := I + 1
y := x
x := x (Σ
bool
)
∗
(y)
Kod(M) ∈ (Σ
bool
)
∗
M M

x
x q
accept
q
reject
x
x x
M L(M) M
L = L(M ) M
L L = L(M ) MT M
M
q
accept
q
reject
•
•
MT
MMT
x
27
28

x q
accept
HMT
{0, 1}
{0, 1}
i
i MT
29
30


L
RE
L
RE

|KodMT|
Σ
bool
KodMT
|(Σ
bool
)
∗
| K odMT ⊆ (Σ
bool
)
∗
Σ
bool
|P((Σ
bool
)
∗
)|
(Σ
bool
)
∗
< |P ((Σ
bool
)
∗
))|,
A B
|A| ≤ |B|,
f A B
|A| = |B|,
|A| ≤ |B| |B| ≤ |A|
A B
|A| < |B|,
|A| ≤ |B|
A B
1
2
3
f A B a, b ∈ A
a 6= b f(a) 6= f(b)
4
f A B b ∈
B
a ∈ A f(a) = b
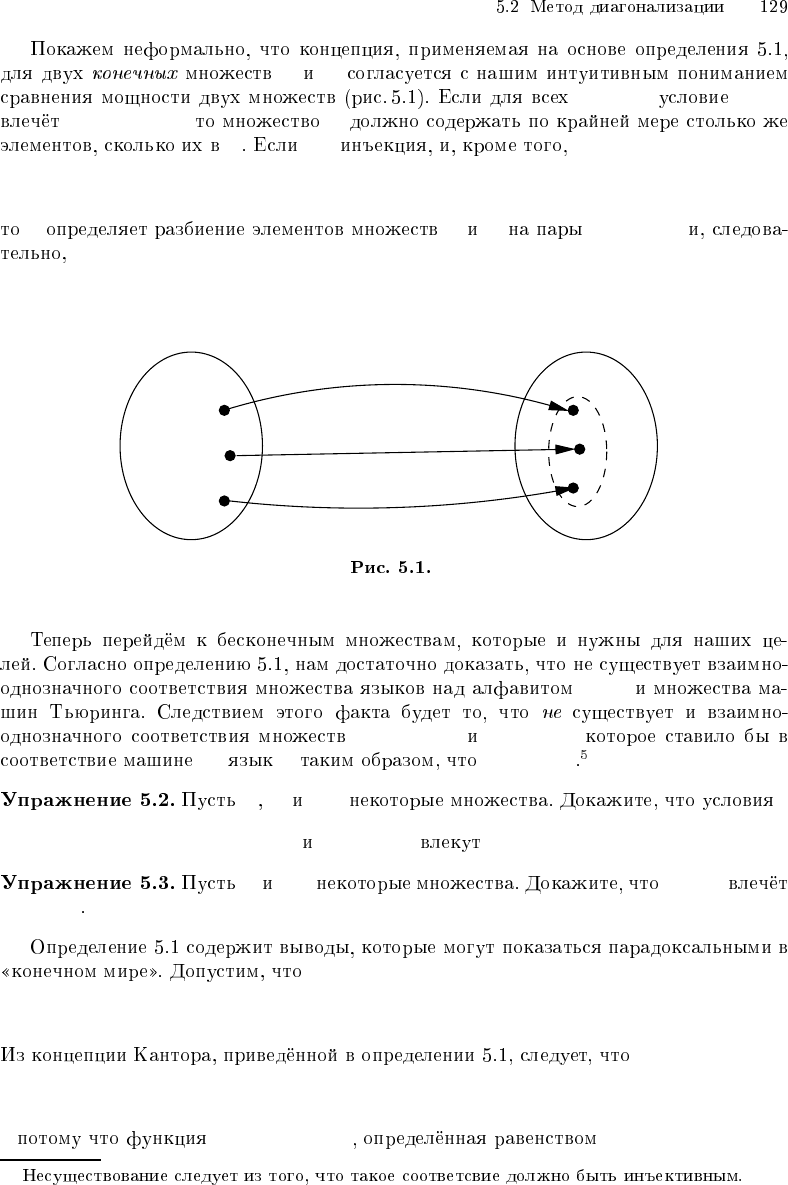
A B
x, y ∈ A x 6= y
f(x) 6= f (y) B
A f
{f(x) | x ∈ A} = B,
f A B (x, f (x))
|A| = |B|.
A
B
f
Σ
bool
P((Σ
bool
)
∗
) Ko dMT
M L L = L(M)
A B C
|B| ≤ |A| |C| ≤ |B| |C| ≤ |A|.
A B A ⊆ B
|A| ≤ |B|
IN
even
= {2i | i ∈ IN
0
}.
|IN
0
| = |IN
even
|
f : IN
0
→ IN
even
5

f(i) = 2i
i ∈ IN IN
0
IN
even
B A
A
|IN
0
| = |IN
even
|
f(i) = 2i (i, 2i) IN
0
IN
even
IN
0
IN
IN
A |A| > |IN|
A
A |A| = |IN
0
|
A A
f : A → IN
0
A
(Σ
bool
)
∗
KodMT
Σ Σ
∗
6
7
8
A ⇐⇒ f : A → IN
0
.
B |B | < |IN
0
|
IN
0
9
A
A
