Громкович Ю. Теоретическая информатика. Введение в теорию автоматов, теорию вычислимости, теорию сложности, теорию алгоритмов, рандомизацию, теорию связи и криптографию
Подождите немного. Документ загружается.


•
•
38

1
2

Σ
bool
•
•
•
3
4
5
6
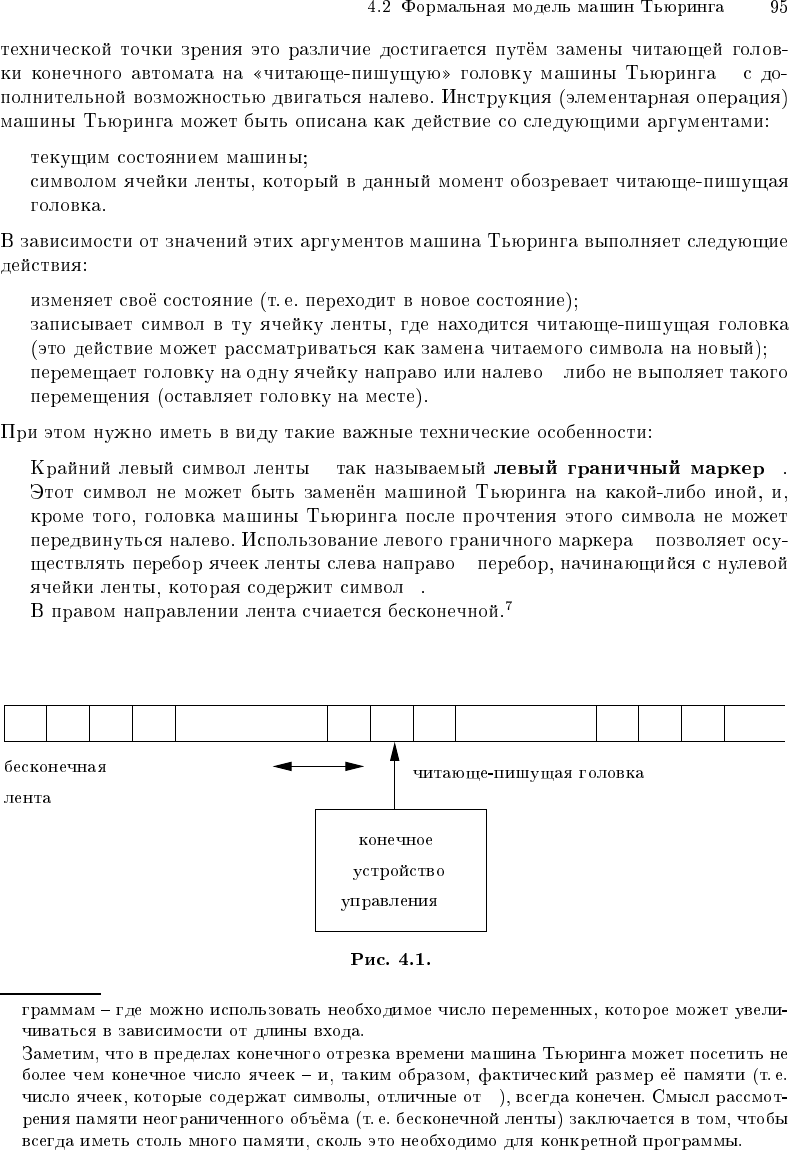
•
•
•
•
•
• ¢
¢
¢
•
0
1
2
3
i
i + 1i − 1
n
n + 1
n + 2
x
1
x
2
x
3
x
i
x
n
x
i−1
x
i+1
tt
··· ······
¢
7
t

( MT) M =
(Q, Σ, Γ, δ, q
0
, q
accept
, q
reject
)
• Q M
• Σ ¢
t
Σ
{Σ
}
• Γ Σ ⊆ Γ ¢,
t
∈ Γ
{Γ
}
• δ : (Q − {q
accept
, q
reject
}) × Γ → Q × Γ × {L, R, N}
M
δ(q, ¢) ∈ Q ×{¢} × {R, N}
q ∈ Q − {q
accept
, q
reject
}
{δ
M M (q, X, Z) ∈
Q ×Γ ×{L, R, N} M p Y ∈ Γ
δ(p, Y ) = (q, X, Z)
p q Y X
Z Z = L M
Z = R Z = N
δ(q, ¢) ∈ Q × {¢} × {R, N}
M ¢
}
• q
0
∈ Q
• q
accept
∈ Q
{M
M q
accept
q
accept
}
• q
reject
∈ Q − {q
accept
}
{ M q
reject
M (
) }
C M
conf(M ) = {¢} · Γ
∗
· Q · Γ
+
∪ Q · {¢} · Γ
∗
.
{
w
1
qaw
2
w
1
∈ {¢}Γ
∗
w
2
∈ Γ
∗
a ∈ Γ q ∈ Q ( )
M q
8
M

¢w
1
aw
2ttt
. . . (|w
1
|+ 1)
a p¢w p ∈ Q w ∈ Γ
∗
¢w
ttt
. . . 0
¢ }
¢ w
1
w
2 t
. . .
t
q
a
M x q
0
¢x
M
|−−
M
|−−
M
⊆
conf(M) × conf(M)
• x
1
x
2
. . . x
i−1
qx
i
x
i+1
. . . x
n
|−−
M
x
1
x
2
. . . x
i−1
pyx
i+1
. . . x
n
δ(q, x
i
) = (p, y, N)
• x
1
x
2
. . . x
i−1
qx
i
x
i+1
. . . x
n
|−−
M
x
1
x
2
. . . x
i−2
px
i−1
yx
i+1
. . . x
n
δ(q, x
i
) = (p, y, L)
• x
1
x
2
. . . x
i−1
qx
i
x
i+1
. . . x
n
|−−
M
x
1
x
2
. . . x
i−1
ypx
i+1
. . . x
n
δ(q, x
i
) = (p, y, R) i < n
• x
1
x
2
. . . x
n−1
qx
n
|−−
M
x
1
x
2
. . . x
n−1
yp
t
δ(q, x
n
) = (p, y, R)
M
C
0
, C
1
, C
2
, . . . C
i
|−−
M
C
i+1
i = 0, 1, 2, . . .
C
0
|−−
M
C
1
|−−
M
···
|−−
M
C
i
i ∈ IN
0
C
0
∗
|−−
M
C
i
.
M x
C
0
= q
0
¢x
w
1
qw
2
q ∈ {q
accept
, q
reject
}
M x
w
1
q
accept
w
2
M x
w
1
q
reject
w
2
M x
9
(q, w, i) ∈ Q × Γ
∗
× IN
0
M
q w
ttt
. . .
i
x
2
x
2
x
2
x
2
x
2
x
2
x
2
x
2
x
i−1
x
i−1
x
i−1
x
i−1
x
i−1
x
i−1
x
n−1
x
n−1
x
i+1
x
i+1
x
i+1
x
i+1
x
i+1
x
i+1
x
i
x
i
x
i
x
n
x
n
x
n
x
n
x
n
x
n
x
n
x
1
x
1
x
1
x
1
x
1
x
1
x
1
x
1
¢
¢
¢
¢
¢
¢
¢
¢
q
q
q
q
p
p
p
p
y
y
y
y
t
t
t
t
t
t
t
t
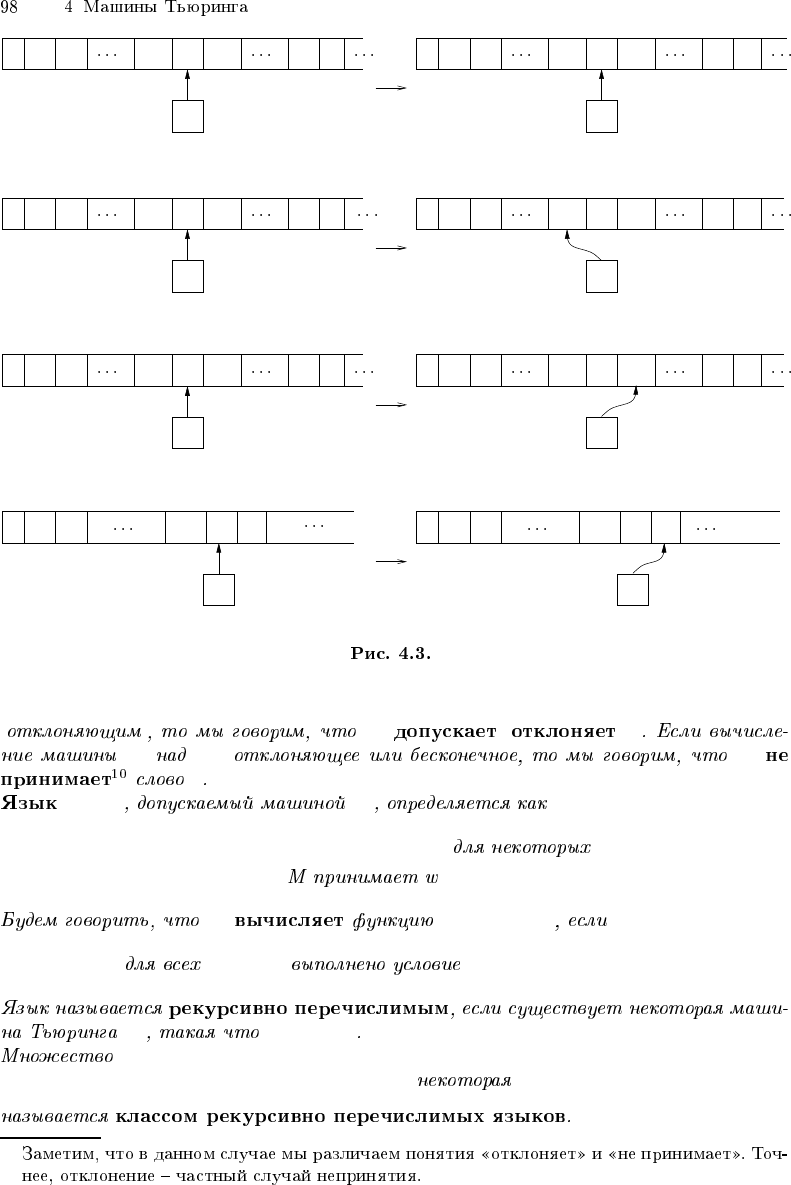
(a) δ(q, x
i
) = (p, y, N)
(b) δ(q, x
i
) = (p, y, L)
(c) δ(q, x
i
) = (p, y, R)
(d) δ(q, x
n
) = (p, y, R)
[ ] M [ ] x
M x M
x
L(M) M
L(M) = {w ∈ Σ
∗
| q
0
¢w
∗
|−−
M
yq
accept
z, y, z ∈ Γ
∗
}
= {w ∈ Σ
∗
| } .
M F : Σ
∗
→ Γ
∗
x ∈ Σ
∗
q
0
¢x
∗
|−−
M
q
accept
¢F (x).
M L = L(M )
L
RE
= {L(M) | M MT}
10

L ⊆ Σ
∗
(Σ, L)
L = L (M ) M
x ∈ Σ
∗
• q
0
¢x
∗
|−−
M
yq
accept
z y, z ∈ Γ
∗
x ∈ L
• q
0
¢x
∗
|−−
M
uq
reject
v
u, v ∈ Γ
∗
x /∈ L
{ M }
M
M
{
}
L
R
= {L(M) | M MT }
Σ
1
Σ
2
F : Σ
∗
1
→ Σ
∗
2
F
(q, ¢w, i) ∈ Q ×{¢}Γ
∗
×IN
0
(q, ¢w, i)
q ¢w
ttt
. . . i
L
middle
= {w ∈ (Σ
bool
)
∗
| w = x1y, |x| = |y|}.
L
middle
1
L
middle
/∈ L(KA)
M L(M) = L
middle
M = (Q, Σ, Γ, δ, q
0
, q
accept
, q
reject
)
Q = {q
0
, q
even
, q
odd
, q
accept
, q
reject
, q
A
, q
B
, q
1
, q
left
, q
right
, q
middle
}
Σ = {0, 1}
Γ = Σ ∪ {¢,
t
} ∪ (Σ × {A, B}) = {0, 1, ¢,
t
0
A
0
B
1
A
1
B
δ(q
0
, ¢) = (q
even
, ¢, R),
δ(q
0
, a) = (q
reject
, a, N)
a ∈ {0, 1,
t
},
δ(q
even
, b) = (q
odd
, b, R) b ∈ Σ,

δ(q
even
,
t
) = (q
reject
,
t
, N),
δ(q
odd
, b) = (q
even
, b, R) b ∈ Σ,
δ(q
odd
,
t
) = (q
B
,
t
, L).
M
q
even
q
odd
M
t
q
even
M
t
q
odd
M q
B
M
a ∈ {0, 1}
a
B
b ∈ Σ
b
A
δ(q
B
, a) = (q
1
,
a
B
, L)
a ∈ {0, 1},
δ(q
1
, a) = (q
left
, a, L)
a ∈ {0, 1},
δ(q
1
, c) = (q
middle
, c, R) c ∈ {¢,
0
A
,
1
A
},
δ(q
middle
,
0
B
) = (q
reject
, 0, N),
δ(q
middle
,
1
B
) = (q
accept
, 1, N),
δ(q
left
, a) = (q
left
, a, L)
a ∈ {0, 1},
δ(q
left
, c) = (q
A
, c, R) c ∈ {
0
A
,
1
A
, ¢},
δ(q
A
, b) = (q
right
,
b
A
, R)
b ∈ { 0, 1},
δ(q
right
, b) = (q
right
, b, R) b ∈ {0 , 1},
δ(q
right
, d) = (q
B
, d, L)
d ∈ {
0
B
,
1
B
}.
(q
right
, ¢)
δ q
reject
q, p ∈ Q a, b ∈ Σ X ∈ {L, R, N}
δ(q, a) = (p, b, X),
M
q p
a → b, X
