Гринберг А.С., Иванюкович В.А., Новыш Б.В., Шешолко В.К. Ситуационный анализ и моделирование на основе информационных технологий баз данных

Подождите немного. Документ загружается.

SELECT DISTINCT Сотрудники.Фамилия, Отделы.Наименование, Сотрудники.Зарплата

FROM Отделы, Сотрудники

WHERE Отделы.Код_отдела = Сотрудники.Код_отдела;

Если необходимо использовать несколько условий связи, то они разделяются

оператором AND).

5.5. Запрос на объединение

Запросы на объединение позволяют представить в одной таблице записи,

созданные несколькими запросами на выборку, записав их один под другим.

Синтаксис запроса на объединение, основой которого является оператор UNION,

имеет вид:

SELECT оператор выборки

UNION SELECT оператор выборки

[GROUP BY условие группировки]

[HAVING итоговое условие]

[UNION SELECT оператор выборки

[GROUP BY условие группировки]

[HAVING итоговое условие]]

[UNION…]

[ORDER BY столбцы сортировки];

При использовании операторов UNION необходимо задавать одинаковый набор

имен полей в списке отбираемых полей, причем, их последовательность должна

быть одинакова в каждом предложении UNIONjSELECT. Модификатор ORDERjBY

может быть использован только один раз в инструкции за последним

оператором UNIONjSELECT. При необходимости в каждый оператор SELECT и

UNIONjSELECT можно вложить операторы GROUP BY и HAVING.

Синтаксис оператора UNION позволяет собирать в одном поле объединенной

таблицы значения из различных доменов:

SELECT Имя_П AS Наименование

FROM Поставщики

WHERE Гор=’Минск’

UNIONjSELECT Имя_Пр AS Наименование

FROM Проекты

WHERE Гор=’Минск’;

Результатом запроса будет таблица из одного столбца, названного

«Наименование», содержащая поставщиков, находящихся в Минске, и

проектов, выполняемых в Минске.

5.6. Вложенные запросы

Вложенные запросы – это применение одного запроса к результирующему

набору записей другого. Для этой цели создается запрос SELECT, в котором

для формирования условия предложения WHERE используется еще один

запрос SELECT. Такие конструкции могут существенно повысить

производительность работы базы данных.

Синтаксис записи вложенных запросов:

SELECT список полей

FROM список таблиц

WHERE [имя таблицы.] имя поля

IN (SELECT оператор выборки

[GROUP BY условие группировки]

[HAVING условие отбора]

[ORDER BY столбцы сортировки]);

5.7. Запросы на изменение. Перекрестные запросы.

Запросы на изменение предназначены для добавления, удаления или

обновления записей, а также для создания таблиц.

Синтаксис запроса на добавление записей:

INSERT INTO таблица-получатель

SELECT [ALL/DISTINCT/DISTINCTROW] список полей

FROM таблица-источник

Если в инструкции на добавление отсутствует предложение WHERE, то в

таблицу-получатель будут добавлены все записи таблицы-источника.

Синтаксис запроса на удаление записей:

DELETE FROM имя таблицы

[WHERE условие удаления];

В этой инструкции предложение WHERE также не обязательное. При его

отсутствии из указанной таблицы будут удалены все записи.

Синтаксис запроса на создание таблицы:

SELECT [ALL/DISTINCT/DISTINCTROW] список полей

INTO новая таблица

FROM исходная таблица

[WHERE условие выбора];

Полную копию исходной таблицы можно создать, указав вместо списка полей

символ * и не используя предложение WHERE.

Запрос на обновление используется для присвоения новых значений отдельным

столбцам при помощи операторов UPDATE и SET:

UPDATE имя таблицы

SET имя_поля_1=значение [,имя_поля_2=значение[,…]]

[WHERE условие обновления];

Перекрестные запросы позволяют создавать различные итоговые запросы,

использующие статистические функции SQL. Когда данные группируются с

помощью перекрестного запроса, можно выбирать значения из заданных полей

или выражений как заголовки столбцов. Для их организации используются

операторы Jet-SQL TRANSFORM и PIVOT:

TRANSFORM статистическая функция (имя поля) [AS наименование]

SELECT [ALL/DISTINCT/DISTINCTROW] список полей

FROM имя таблицы

PIVOT Format (имя поля, “тип форматирования”)

[IN список значений];

Используя SQL, можно обновить данные или удалить записи таблиц,

относящихся к другим базам данных любого типа (FoxPro, dBase, Paradox,…).

Для определения файла внешней таблицы или базы данных используется

оператор IN. Средствами MS ACCESS можно создавать или изменять таблицы

dBase или Paradox, указав в операторе IN путь к их файлу и тип файла.

Стандарт ANSI SQL-92 содержит около 200 ключевых слов, а в JetjSQL

используется менее половины из них. Многие операции организуются в JetjSQL

выражениями, создаваемыми набором операторов или функциями MS ACCESS

VBA (Visual Basic for Applications). Кроме того, в JetjSQL зарезервирован набор

слов, не имеющих аналогов в ANSI SQL-92. Тем не менее, JetjSQL

соответствует стандарту SQL-92.

Все ключевые слова ANSIjSQL, поддерживаемые используемой модификацией

JetjSQL, а также зарезервированные уникальные слова, можно найти в

справочных пособиях (в том числе и в системе помощи MS ACCESS). Слова,

зарезервированные в JetjSQL, нельзя использовать в качестве имен таблиц,

полей или переменных.

Возможности современных реляционных баз данных позволяют осуществлять

эффективное управление данными, используя одновременно два языка – язык

реляционных баз данных SQL и язык программирования VBA, разработанный

для программных продуктов пакета MS Office.

6 . ПР О Е К Т И Р О В А Н И Е Р Е Л Я Ц И О Н Н Ы Х Б АЗ Д А Н Н Ы Х

6.1. Цели проектирования

Как правило, администратор баз данных (даже если это группа лиц)

практически не в состоянии охватить и осмыслить все информационные

требования сотрудников организации – будущих пользователей системы.

Поэтому информационные системы больших организаций состоят из

некоторого количества баз данных, нередко распределенных между

несколькими взаимосвязанными ЭВМ различных подразделений.

Отдельные базы данных могут объединять все данные, необходимые для

решения одной или нескольких прикладных задач, или данные, относящиеся к

какой-либо предметной области (например, финансам, студентам,

преподавателям, кулинарии и т.п.). Первые обычно называют прикладными

базами данных, а вторые – предметными базами данных (соотносящимся с

предметами организации, а не с ее информационными приложениями).

Предметные базы данных должны обеспечивать поддержку любых

текущих и будущих приложений. Вследствие этого предметные базы данных

создают основу для обработки неформализованных, изменяющихся и

неизвестных запросов и приложений (приложений, для которых невозможно

заранее определить требования к данным). Такая гибкость и

приспосабливаемость позволяет создавать на основе предметных баз данных

достаточно стабильные информационные системы, т.е. системы, в которых

большинство изменений можно осуществить без вынужденного переписывания

старых приложений.

Осуществляя проектирование баз данных на текущих и предвидимых

приложениях, можно существенно ускорить создание высокоэффективной

информационной системы, т.е. системы, структура которой учитывает наиболее

часто встречающиеся пути доступа к данным. Поэтому прикладное

проектирование до сих пор привлекает разработчиков. Однако по мере роста

числа приложений таких информационных систем быстро увеличивается число

прикладных баз данных, резко возрастает уровень дублирования данных и

повышается стоимость их ведения.

Желание достичь и гибкости, и эффективности привело к формированию

методологии проектирования, использующей как предметный, так и

прикладной подходы. В общем случае предметный подход используется для

построения первоначальной информационной структуры, а прикладной – для ее

совершенствования с целью повышения эффективности обработки данных.

Далее будут рассматриваться только вопросы, связанные с

проектированием отдельных реляционных предметных баз данных.

Основная цель проектирования баз данных – это сокращение

избыточности хранимых данных, а следовательно, экономия объема

используемой памяти, уменьшение затрат на многократные операции

обновления избыточных копий и устранение возможности возникновения

противоречий из-за хранения в разных местах сведений об одном и том же

объекте. Так называемый "чистый" проект базы данных ("Каждый факт в одном

месте") можно создать, используя методологию нормализации отношений. И

хотя нормализация должна использоваться на завершающей проверочной

стадии проектирования баз данных, мы начнем обсуждение вопросов

проектирования с рассмотрения причин, которые заставили Кодда создать

основы теории нормализации.

В процессе проектирования баз данных могут возникнуть следующие

проблемы:

1. Избыточность – некоторые данные или группы данных могут многократно

повторяться.

2. Аномалии обновления – вследствие избыточности данных при их

обновлении необходимо просматривать все данные, тем не менее, может

возникнуть ситуация, когда не все данные будут обновлены (потенциальная

противоречивость данных).

3. Аномалии включения – возможна ситуация, когда в базу нельзя ввести

данные, прежде чем не будут получены и введены некоторые

дополнительные сведения.

4. Аномалии удаления – обратная проблема может возникнуть при удалении

некоторых данных (возможна потеря полезной информации).

Такие проблемы разрешаются в процессе нормализации отношений.

6.2. Нормализация отношений

Нормализация – это разбиение таблицы на две или более, обладающих

лучшими свойствами при добавлении, изменении и удалении данных.

Окончательная цель нормализации сводится к получению такого проекта базы

данных, в котором «каждый факт появляется лишь в одном месте», т.е.

исключена избыточность информации. Это делается не столько с целью

экономии памяти, сколько для исключения возможной противоречивости

хранимых данных.

Каждая таблица в реляционной базе данных удовлетворяет условию, в

соответствии с которым в позиции на пересечении каждой строки и столбца

таблицы всегда находится единственное атомарное значение, и никогда не

может быть множества таких значений. Любая таблица, удовлетворяющая

этому условию, называется нормализованной. Фактически, ненормализованные

таблицы, т.е. таблицы, содержащие повторяющиеся группы, даже не

допускаются в реляционной базе данных.

Всякая нормализованная таблица автоматически считается таблицей в

первой нормальной форме, сокращенно 1НФ. Таким образом, строго говоря,

"нормализованная" и "находящаяся в 1НФ" означают одно и то же. Однако на

практике термин "нормализованная" часто используется в более узком смысле

– "полностью нормализованная", который означает, что в проекте не

нарушаются никакие принципы нормализации.

Теперь в дополнение к 1НФ можно определить дальнейшие уровни

нормализации – вторую нормальную форму (2НФ), третью нормальную форму

(3НФ) и т.д. Считается, что таблица находится во 2НФ, если она находится в

1НФ и удовлетворяет, кроме того, некоторому дополнительному условию, суть

которого будет рассмотрена ниже. Таблица находится в 3НФ, если она

находится в 2НФ и, помимо этого, удовлетворяет другому дополнительному

условию и т.д.

Таким образом, каждая нормальная форма является в некотором смысле

более ограниченной, но и более желательной, чем предшествующая. Это

связано с тем, что (n+1)-я нормальная форма не обладает некоторыми

непривлекательными особенностями, свойственными n-й нормальной форме.

Общий смысл дополнительного условия, налагаемого на (n+1)-ю нормальную

форму по отношению к n-й нормальной форме, состоит в исключении этих

непривлекательных особенностей.

Процедура нормализации отношений обратима. Например, множество

отношений, находящихся в 3НФ, можно преобразовать в отношения,

находящиеся в 2НФ. Это очень важное свойство нормализации означает, что в

процессе нормализации информация не утрачивается.

Теория нормализации основывается на наличии той или иной зависимости

между полями таблицы. Особое внимание уделяется функциональным и

многозначным зависимостям и зависимостям соединений.

6.3. Функциональные зависимости

Пусть X и Y – произвольные подмножества множества атрибутов

отношения R. Y функционально зависит от X тогда и только тогда, когда

каждое значение множества X связано в точности с одним значением

множества Y. Обозначение: XY (читается как «X функционально определяет

Y»). Левая и правая части символической записи называются детерминантом и

зависимой частью соответственно.

Иначе говоря, если два кортежа отношения R совпадают по значению X, то

они также совпадают и по значению Y. Для пояснения рассмотрим несколько

измененную версию таблицы отношения поставок, изображенной на рис. 3.5.3.

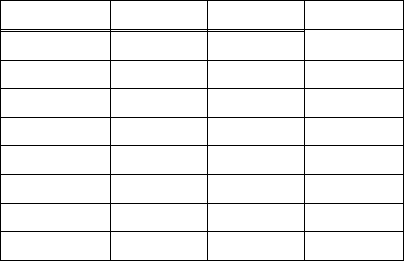
П№ Гор Д№ Кол

П1 Брест Д1 100

П1 Брест Д2 100

П2 Минск Д1 200

П2 Минск Д2 200

П3 Гродно Д2 300

П4 Минск Д2 400

П4 Минск Д4 400

П4 Минск Д5 400

Рис. 6.3.1. Таблица отношения поставок ПОС

Все кортежи отношения ПОС с одинаковым значением атрибута П№ имеют

одинаковые значения атрибута Гор. Значит, атрибуты Гор функционально зависят

от атрибутов П№: {П№}{Гор}. Более того, в этом отношении присутствуют и

другие постоянные функциональные зависимости: {П№,Д№}{Кол}, {П№,Д№}{Гор},

{П№,Д№}{Гор,Кол}, {П№,Д№}{П№,Д№,Гор,Кол}, {П№,Д№}{П№}, а также зависимости,

которые являются функциональными в любой данный момент, но не все время

– {П№}{Кол} и {Гор}{П№}.

Отметим, что если X является потенциальным ключом отношения R, то

все атрибуты Y отношения R должны быть функционально зависимы от X (это

следствие из определения потенциального ключа). Фактически, если отношение

R удовлетворяет функциональной зависимости АВ и А не является

потенциальным ключом, то R будет характеризоваться некоторой

избыточностью. Например, в отношении ПОС сведения о том, что каждый

поставщик находится в определенном городе будут повторяться много раз.

Функциональные зависимости являются ограничениями целостности,

поэтому при каждом обновлении базы данных они должны быть проверены.

Очевидным способом сокращения множества функциональных зависимостей

является исключение тривиальных зависимостей, т.е. таких, которые не могут

не выполняться. Например, {П№,Д№}{П№}. Функциональная зависимость

является тривиальной тогда и только тогда, когда правая часть символьной

записи является подмножеством левой части. Такие зависимости не

представляют никакого интереса с практической точки зрения.

Неприводимые зависимости. Атрибут В неприводимо зависим от

составного атрибута А, если он функционально зависит от А и не зависит

функционально от любого подмножества атрибута А. В ранних публикациях

вместо термина неприводимая зависимость использовался термин полная

функциональная зависимость.

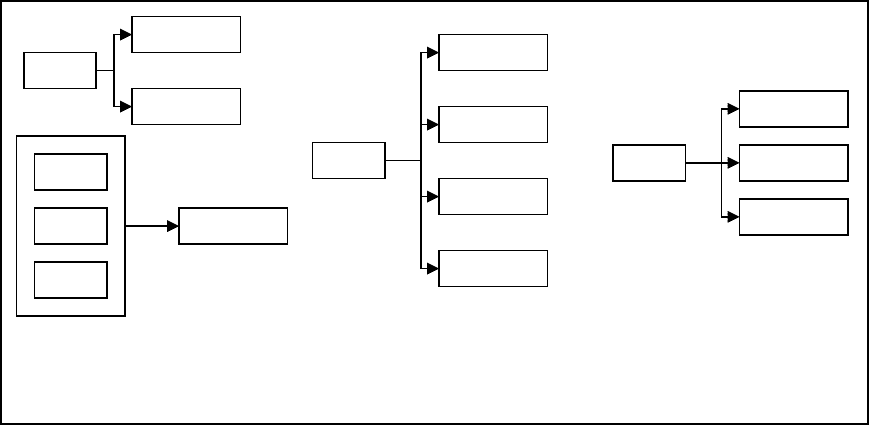
Функциональные зависимости могут быть изображены при помощи

диаграмм. Для базы данных поставщиков и деталей (рис. 3.5.3) диаграмма

функциональных зависимостей изображена на рис.6.3.2.

Каждая стрелка на диаграмме начинается с первичного ключа

соответствующего отношения. На диаграмме возможны и другие стрелки. В

таком случае процедуру нормализации можно неформально охарактеризовать

как процедуру исключения стрелок, которые начинаются не на первичном

ключе.

6.4. Нормальные формы, обоснованные функциональными

зависимостями

В п.j6.2 было дано нестрогое определение первой нормальной формы

(1НФ). Приведем более строгое ее определение, а также определения других

нормальных форм.

Таблица находится в первой нормальной форме (1НФ) тогда и только

тогда, когда ни одна из ее строк не содержит в любом своем поле более

одного значения и ни одно из ее ключевых полей не пусто.

Этим требованиям не удовлетворяет таблица (данные в поле Д№ не

атомарны):

Пр№

Имя_Пр

Имя_Рук

П№

Кол

Д№

Имя_Д

Цвет

Вес

Гор

П№

Имя_П

Статус

Гор

Рис. 6.3.2. Диаграмма функциональных зависимостей для

отношений Проекты, Детали, Поставщики и Поставки

(см.jрис.j3.5.3)

Пр№

Д№

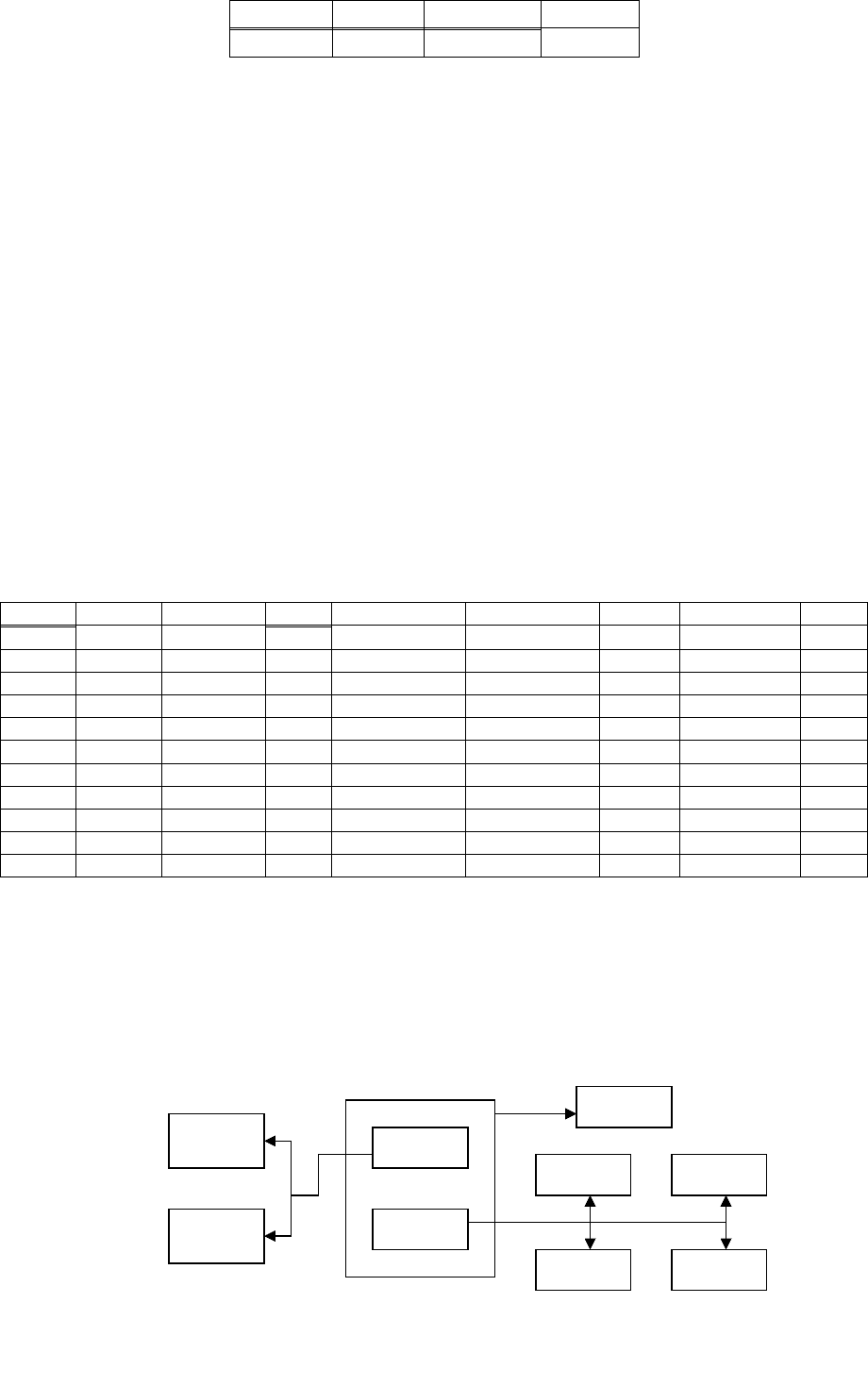
П№ Гор Д№ Кол

П4 Минск Д2,Д4,Д5 400

Рис.j6.4.1. Пример таблицы, которая не является отношением

Такие таблицы даже не рассматриваются в реляционных моделях.

Если мы разрабатываем реляционную базу данных, то на первом этапе

может быть создана таблица, объединяющая все рассматриваемые данные,

например, Поставщики, Детали, Поставки. Таблица на рис.j6.4.2 представляет

собой экземпляр корректного отношения. Его называют универсальным

отношением проектируемой базы данных. В одно универсальное отношение

включаются все представляющие интерес атрибуты и оно может содержать все

данные, которые предполагается размещать в базе данных в будущем. Для

малых баз данных универсальное отношение может использоваться в качестве

отправной точки при их проектировании. Первичным ключом таблицы

является комбинация полей П№ и Д№. Эта таблица удовлетворяет всем

требованиям 1НФ.

П№ Статус Гор_П Д№ Имя_Д Цв Вес Гор_Д Кол

П1 20 Брест Д1 Тестер Черный 250 Борисов 300

П1 20 Брест Д2 Дозиметр Серый 700 Минск 200

П1 20 Брест Д3 Радиометр Черный 1400 Минск 400

П1 20 Брест Д4 Часы Желтый 140 Брест 200

П1 20 Брест Д5 Рулетка Красный 200 Пинск 100

П1 20 Брест Д6 Лом Черный 5000 Могилев 100

П2 10 Минск Д1 Тестер Черный 250 Борисов 300

П2 10 Минск Д2 Дозиметр Серый 700 Минск 400

П3 30 Гродно Д2 Дозиметр Серый 700 Минск 200

П4 10 Минск Д2 Дозиметр Серый 700 Минск 200

П4 10 Минск Д4 Часы Желтый 140 Брест 300

Рис.j6.4.2. Отношение в первой нормальной форме

Диаграмма функциональных зависимостей такого отношения может иметь

вид, изображенный на рис.j6.4.3 (будем предполагать, что статус поставщика

определяется городом).

Рис.j6.4.3. Диаграмма функциональных зависимостей

отношения в 1НФ

П№

Д№

Гор_П

Статус

Цв

ВесГор_Д

Кол

Имя_Д