Гринберг А.С., Иванюкович В.А., Новыш Б.В., Шешолко В.К. Ситуационный анализ и моделирование на основе информационных технологий баз данных
Подождите немного. Документ загружается.

Отношение R(X,Y,...,Z) удовлетворяет зависимости соединения *(X,Y,...,Z)
в том и только в том случае, когда R восстанавливается без потерь путем
соединения своих проекций на X, Y, ..., Z.
Сейчас теорему Фейгина можно сформулировать в таком виде:
Отношение R(А,В,С) удовлетворяет зависимости соединения *(АВ,АС)
тогда и только тогда, когда оно удовлетворяет многозначным зависимостям
АВ и АС.
Зависимость соединения является обобщением понятия многозначной
зависимости. Более того, это наиболее общая форма зависимости.
Возвращаясь к отношению Поставщики-Детали-Проект, можно
обнаружить, что оно содержит зависимость соединения
ПДПрj*(ПД,jДПр,jПрП), которая не является ни функциональной, ни
многозначной зависимостью. Такое отношение рекомендуется
декомпозировать на проекции, заданные зависимостью соединения. Такой
процесс декомпозиции может повторяться до тех пор, пока все
результирующие отношения не будут находиться в пятой нормальной форме
(5НФ).
Отношение R находится в пятой нормальной форме в том и только в
том случае, когда любая зависимость соединения в R следует из
существования некоторого возможного ключа в R.
Менее строгое определение 5НФ:
Таблица находится в пятой нормальной форме (5НФ) тогда и только
тогда, когда в каждой ее полной декомпозиции все проекции содержат
возможный ключ. Таблица, не имеющая ни одной полной декомпозиции, также
находится в 5НФ.
Четвертая нормальная форма (4НФ) является частным случаем 5НФ, когда
полная декомпозиция должна быть соединением ровно двух проекций. Весьма
не просто подобрать реальную таблицу, которая находилась бы в 4НФ, но не
была бы в 5НФ.
Для заданного отношения R можно утверждать, что оно находится в 5НФ
при условии, что известны все потенциальные ключи и все зависимости
101
соединения. Однако нет алгоритма, позволяющего определять все зависимости
соединения. Но такие отношения чрезвычайно редки на практике.
Пятая нормальная форма – это последняя нормальная форма, которую
можно получить путем декомпозиции. Ее условия достаточно нетривиальны, но
на практике 5НФ не используется.
6.7. Процедура нормализации и проектирования
Мы рассмотрели технологию декомпозиции без потерь, применяемую для
проектирования базы данных. Основная идея этой технологии состоит в
систематическом приведении первоначального отношения, находящегося в
1НФ, к набору меньших отношений, который в некотором заданном смысле
эквивалентен исходному отношению, но более предпочтителен. Каждый этап
процесса приведения состоит из разбиения на проекции отношений,
полученных на предыдущем этапе. При этом заданные ограничения
используются на каждом шаге процедуры нормализации для выбора проекций
на следующем этапе. Нормализация – это разбиение отношения (таблицы) на
несколько отношений, обладающих лучшими свойствами при обновлении,
включении и удалении данных. Этот процесс последовательной замены
таблицы ее полными декомпозициями выполняется до тех пор, пока все они не
будут находиться в 5НФ. В общем, можно выделить следующие цели процесса
нормализации:
исключение некоторых типов избыточности;
устранение некоторых аномалий обновления;
проектирование макета базы данных, который являлся бы "хорошим"
представлением реального мира, был интуитивно понятен и служил хорошей
основой для дальнейшего развития;
упрощение процесса наложения ограничений целостности.
На практике достаточно привести таблицы к НФБК и с большой гарантией
можно считать, что они находятся в 5НФ. Перечислим основные правила,
которые используются в процедуре нормализации.
1. Унифицированное отношение должно быть приведено к 1НФ.
2. Отношения в 1НФ следует разбить на проекции для исключения всех
функциональных зависимостей, которые не являются неприводимыми.
102
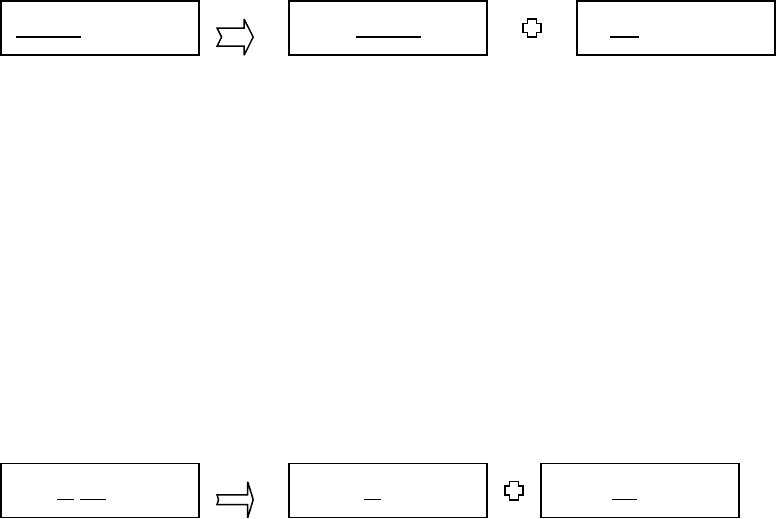
Другими словами, если отношение имеет составной первичный ключ вида
(К1,К2) и включает также поле F, которое функционально зависит от части
этого ключа, например, от К2, но не от полного ключа, то в этом случае
рекомендуется сформировать другое отношение, содержащее К2 и F
(первичный ключ – К2), и удалить F из первоначального отношения:
В результате такого действия будет получен набор отношений в 2НФ.
3. Отношения в 2НФ следует разбить на проекции для исключения любых
транзитивных функциональных зависимостей. Другими словами, если
отношение имеет потенциальный ключ К, не являющийся потенциальным
ключом атрибут F1, который функционально зависит от К, и другой
неключевой атрибут F2, который функционально зависит от F1, то
рекомендуется удалить из исходного отношения атрибут F2 и сформировать
другое отношение, содержащее F1 и F2, с первичным ключом F1.
В результате будет получен набор отношений в 3НФ.
4. Отношения в 3НФ рекомендуется разбить на проекции для исключения
любых оставшихся функциональных зависимостей, в которых
детерминанты не являются потенциальными ключами. В результате будет
получен набор отношений в НФБК.
5. Отношения в НФБК следует разбить на проекции для исключения всех
многозначных зависимостей, которые не являются функциональными
зависимостями. В результате будет получен набор отношений в 4НФ (на
практике такие многозначные зависимости обычно исключаются при
создании исходных отношений, отделяя независимые повторяющиеся
группы).
6. Отношения в 4НФ следует разбить на проекции для исключения любых
зависимостей соединения, которые не подразумеваются потенциальными
K1,K2,F (K2F) K1,K2 K2,F (K2F)
K,F1,F2 K,F1 F1,F2
103
ключами, если их можно выявить. Таким образом будет получен набор
отношений в 5НФ.
При следовании предложенным правилам необходимо помнить, что
разбиение на проекции должно выполняться без потерь и с сохранением
зависимости.
Предложенные рекомендации по поводу нормализации являются всего
лишь рекомендациями и, возможно, могут существовать ситуации, когда
нормализацию не следует выполнять от начала до конца. У такого
предположения есть несколько оснований. Во-первых, нормализация может
помочь получить в простой форме некоторые ограничения целостности, но
кроме функциональных и многозначных зависимостей и зависимости
соединения, на практике могут существовать и другие типы зависимостей. Во-
вторых, для выбора предпочтительной декомпозиции существует немного
критериев. В-третьих, процесс нормализации и сохранение зависимости не
всегда совместимы. В-четвертых, не всякую избыточность можно устранить в
процессе нормализации.
Проектирование систем баз данных начинается с построения
инфологической модели данных, т.е. идентификации сущностей. Затем
необходимо выполнить следующие шаги процедуры проектирования:
1. Представить каждую независимую сущность таблицей базы данных
(базовой таблицей) и определить первичный ключ этой базовой таблицы.
2. Представить каждую ассоциацию (связь между сущностями) как
базовую таблицу. Использовать в этой таблице внешние ключи для
идентификации участников ассоциации и специфицировать ограничения,
связанные с каждым из этих внешних ключей.
3. Представить свойства сущностей как базовые таблицы с внешним
ключом, идентифицирующим соответствующие сущности. Специфицировать
ограничения на внешние ключи этих таблиц и их первичные ключи.
4. Представить каждое свойство как поле в базовой таблице,
представляющей сущность, которая непосредственно описывается этим
свойством.
104
5. Для того чтобы исключить в проекте непреднамеренные нарушения
каких-либо принципов нормализации, выполнить процедуру нормализации.
6. Если в процессе нормализации было произведено разделение каких-либо
таблиц, то следует модифицировать инфологическую модель базы данных и
повторить перечисленные шаги.
7. Указать ограничения целостности проектируемой базы данных и дать
(если это необходимо) краткое описание полученных таблиц и их полей.
Для наглядного представления структуры проектируемой системы может
быть использован язык инфологического моделирования "Таблица-связь",
используемый в наиболее распространенных реляционных базах данных. В нем
все сущности изображаются одностолбцовыми таблицами с заголовками,
состоящими из имени сущности. Строки таблицы – это перечень атрибутов
сущности, а те из них, которые составляют первичный ключ, выделяются.
Связи между сущностями указываются стрелками, направленными от
первичных ключей или их составляющих.
7 . ПР И М Е Р П Р О Е К Т И Р О В А Н И Я
Б А З Ы Д А Н Н Ы Х
7.1. Назначение и предметная область
База данных предназначена для хранения информации о персонале
некоторой компании.
В компании есть несколько отделов.
В каждом отделе есть несколько сотрудников, несколько проектов и
несколько кабинетов.
Каждый сотрудник имеет несколько заданий. Для каждого задания
существует ведомость с перечнем денежных сумм, полученных сотрудником за
выполнение данной работы.
В каждом кабинете есть несколько телефонов.
В базе данных должна храниться следующая информация:
105
Для каждого отдела: уникальный номер отдела, бюджет и уникальный
номер руководителя отдела.
Для каждого сотрудника: уникальный номер сотрудника, номер текущего
проекта, номер кабинета, номер телефона, а также название выполняемой
работы вместе с датами и размерами всех оплат, полученных за выполнение
данной работы.
Для каждого проекта: уникальный номер проекта и бюджет.
Для каждого кабинета: уникальный номер кабинета, площадь, номера всех
телефонов.
Семантические утверждения:
Ни один сотрудник не является одновременно руководителем нескольких
отделов.
Ни один сотрудник не работает одновременно более чем в одном отделе.
Ни один сотрудник не работает одновременно более чем с одним проектом.
Ни один сотрудник не имеет одновременно более одного кабинета.
Ни один сотрудник не имеет одновременно более одного телефона.
Ни один сотрудник не имеет одновременно более одного задания.
Ни один проект не дается одновременно более чем одному отделу.
Ни один кабинет не относится одновременно более чем к одному отделу.
7.2. Проектирование базы данных
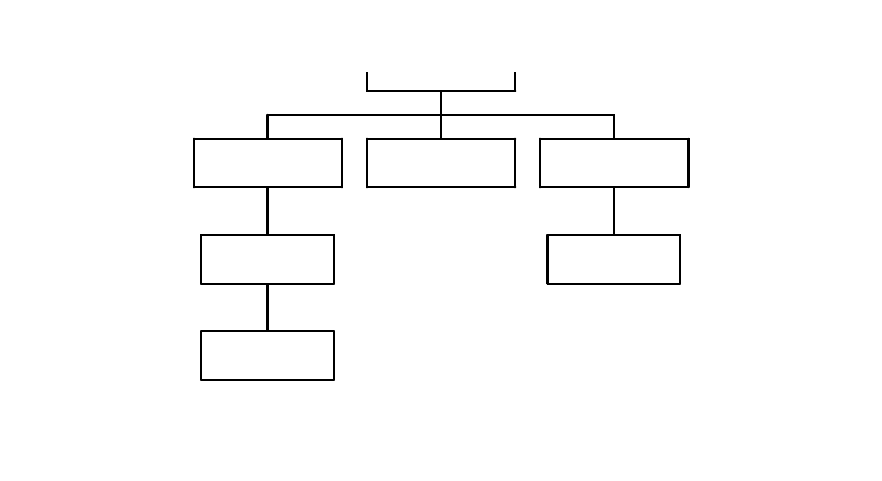
Анализ определенных выше объектов и атрибутов позволяет выделить
сущности проектируемой базы данных и построить ее инфологическую модель
на языке "Таблицы-связи" (рис.7.2.1).
Исходную иерархическую структуру можно рассматривать как
ненормализованное отношение:
ОТДЕЛЫ (ОТД№, БЮДЖЕТ_О, РУК№, СОТРУДНИКИ, ПРОЕКТЫ, КАБИНЕТЫ)
CANDIDATE KEY (ОТД№)
CANDIDATE KEY (РУК№)
Здесь смысл атрибутов ОТД№ (уникальный номер отдела), БЮДЖЕТ_О, РУК№
(номер руководителя) понятен из названий, а домены, соответствующие
атрибутам СОТРУДНИКИ, ПРОЕКТЫ, КАБИНЕТЫ состоят из значений-отношений. Мы
можем расписать их вложенные атрибуты:
106
.ОТДЕЛЫ (ОТД№, БЮДЖЕТ, РУК№,
СОТРУДНИКИ (СОТР№, ПРОЕКТ№, КАБ№, ТЕЛ№, РАБОТА (ТЕМА, ОПЛАТА
(ДАТА, СУММА))),
ПРОЕКТЫ (ПРОЕКТ№, БЮДЖЕТ_П),
КАБИНЕТЫ (КАБ№, ПЛОЩАДЬ, ТЕЛЕФОН (ТЕЛ№)))
CANDIDATE KEY (ОТД№)
CANDIDATE KEY (РУК№)
Сейчас можно привести это отношение к набору отношений в 1НФ. При
этом, рассматривая каждое значение-отношение отдельно, мы исключаем все
многозначные зависимости, которые не являются функциональными
зависимостями.
ОТДЕЛЫ1 (ОТД№, БЮДЖЕТ_О, РУК№)
PRIMARY KEY (ОТД№)
ALTERNATE KEY (РУК№)
СОТРУДН1 (СОТР№, ОТД№, ПРОЕКТ№, КАБ№, ТЕЛ№)
PRIMARY KEY (СОТР№)
РАБОТА1 (ТЕМА, СОТР№)
PRIMARY KEY (ТЕМА, СОТР№)
ОПЛАТА1 (СОТР№, ТЕМА, ДАТА, СУММА)
PRIMARY KEY (СОТР№, ТЕМА, ДАТА)
ПРОЕКТЫ1 (ПРОЕКТ№, БЮДЖЕТ_П, ОТД№)
PRIMARY KEY (ПРОЕКТ№)
КАБИНЕТЫ1 (КАБ№, ПЛОЩАДЬ, ОТД№)
PRIMARY KEY (КАБ№)
ТЕЛЕФОНЫ1 (ТЕЛ№, КАБ№)
PRIMARY KEY (ТЕЛ№)
Далее, можно привести отношения, находящиеся в 1НФ, к эквивалентной
совокупности отношений в 2НФ, исключая неприводимые зависимости.
В е д о м о с т ь
З а д а н и я
С о т р у д н и к и
П р о е к т ы
Т е л е ф о н ы
К а б и н е т ы
О т д е л ы
Рис.7.2.1.jНенормализованное представление
информации о персонале компании, которая
107

Отношения ОТДЕЛЫ1, СОТРУДН1, ОПЛАТА1, ПРОЕКТЫ1, КАБИНЕТЫ1 и ТЕЛЕФОНЫ1 уже
находятся в 2НФ.
Отношение РАБОТА1 является проекцией отношения ОПЛАТА1,
следовательно, оно несет избыточную информацию и его можно удалить без
потери данных. В то же время, отношение ТЕЛЕФОНЫ1 является проекцией
отношения СОТРУДН1, но при его удалении появятся аномалии обновления –
данные о телефонах не будут существовать без данных о конкретных
сотрудниках.
Покажем сейчас структуру базы данных, отношения которой приведены к
2НФ, используя язык моделирования «Таблица-Связь», который применяется в
СУБД MSjACCESS:
ОТДЕ
Л2
СОТР
УДН2
ОП
ЛАТА2
ПРОЕ
КТ2
КАБИ
НЕТ2
ТЕЛЕ
ФОН2
ОТД
СОТР
СОТ
ПРОЕ
КАБ№
ТЕЛ№
БЮД
ЖЕТ_О
ОТД
№
ДАТ
А
ОТД
№
ПЛОЩ
АДЬ
КАБ№
РУК
№
ПРОЕ
КТ№
ТЕМ
А
БЮД
ЖЕТ_П
ОТД№
КАБ
№
СУ
ММА
ТЕЛ№
Далее, исключая транзитивные зависимости, можно привести отношения,
находящиеся в 2НФ, к эквивалентной совокупности отношений в 3НФ.
Единственным отношением, которое не находится в 3НФ, является отношение
СОТРУДН, в котором атрибуты КАБ№ и ОТД№ транзитивно зависят от первичного
ключа СОТР№ – КАБ№ через ТЕЛ№, а ОТД№ через ПРОЕКТ№ и, кроме того, через КАБ№
и ТЕЛ№. Тогда отношение СОТРУДН можно заменить совокупностью проекций,
находящихся в 3НФ:
СОТРУДН3 (СОТР№, ПРОЕКТ№, ТЕЛ№)
PRIMARY KEY (СОТР№)
X (ТЕЛ№, КАБ№)
PRIMARY KEY (ТЕЛ№)
Y (ПРОЕКТ№, ОТД№)
PRIMARY KEY (ПРОЕКТ№)
Z (КАБ№, ОТД№)
PRIMARY KEY (КАБ№)
108
Но отношение X – аналог отношения ТЕЛЕФОН2, Y – проекции
отношения ПРОЕКТ2, Z – проекции КАБИНЕТ2 и, значит, могут быть удалены
из модели базы данных. Следовательно, модель базы данных, отношения
которой приведены к 3НФ, будет выглядеть так:
ОТДЕЛЫ3 (ОТД№, БЮДЖЕТ_О, РУК№)
PRIMARY KEY (ОТД№)
ALTERNATE KEY (РУК№)
СОТРУДН3 (СОТР№, ПРОЕКТ№, ТЕЛ№)
PRIMARY KEY (СОТР№)
ОПЛАТА3 (СОТР№, ТЕМА, ДАТА, СУММА)
PRIMARY KEY (СОТР№, ТЕМА, ДАТА)
ПРОЕКТЫ3 (ПРОЕКТ№, БЮДЖЕТ_П, ОТД№)
PRIMARY KEY (ПРОЕКТ№)
КАБИНЕТЫ3 (КАБ№, ПЛОЩАДЬ, ОТД№)
PRIMARY KEY (КАБ№)
ТЕЛЕФОНЫ3 (ТЕЛ№, КАБ№)
PRIMARY KEY (ТЕЛ№)
Каждое из этих отношений уже находится в НФБК. Более того, они
находятся в 4НФ – от возможных многозначных зависимостей мы избавились
на этапе приведения модели к 1НФ). Все отношения не содержат видимых
аномалий и поэтому можно предполагать, что база данных сконструирована
правильно.
8 . ДО П О Л Н И Т Е Л Ь Н Ы Е А С П Е К Т Ы
8.1. Объектно-ориентированный подход
При структурном программировании последовательно выполняются
операторы, записываемые программистом в соответствии со схемой решения
поставленной задачи. Объектно-ориентированное программирование (ООП)
делает акцент не на программные структуры, а на объекты. Программист
создает нужные объекты, описывает действия с ними и их реакцию на действия
пользователя. Любую программу можно написать, используя тот или иной
набор объектов, обеспечивающих выполнение тех или иных функций.
109
Объектно-ориентированные СУБД берут свое начало от объектно-
ориентированных языков программирования. Основная идея, объединяющая
эти две области, состоит в том, что пользователям приходится оперировать не
понятиями, связанными с аппаратным обеспечением, например биты и байты
или записи и поля, а понятиями, которые более всего отвечают структуре
реального мира, а именно объектами и операциями, определенными для этих
объектов. Иначе говоря, фундаментальной идеей объектно-ориентированного
подхода является повышение уровня абстракции, а его смысл заключается в
создании объектов и удобных средств манипуляции ими.
Для упрощения восприятия связи объектно-ориентированного подхода и
СУБД можно сопоставить (достаточно грубо) их терминологию:
Объектно-ориентированная
терминология
Терминология традиционного
программирования
Объект Переменная (если объект "изменчив") или
значение (если объект "неизменчив")
Объектный класс Тип данных
Метод Функция
Событие Вызов функции
В настоящее время большинство современных коммерческих СУБД
используют элементы ООП для упрощения и ускорения создания различных
элементов и выполнения операций, но нет объектно-ориентированных систем
управления в «чистом виде». В первую очередь потому, что реляционный
подход обладает значительным преимуществом по сравнению с объектно-
ориентированным – в нем предусмотрено выполнение незапланированных
запросов. Тем не менее, выполняется множество исследовательских работ в
этом направлении. Однако наиболее перспективным представляется поиск
возможностей совместного использования реляционного и объектно-
ориентированного подходов. Сближение двух подходов следует выполнять на
основе реляционной модели (которая служит основой всей современной
области изучения баз данных). Это значит, что следует изменить реляционную
систему, чтобы в нее вошли лучшие черты объектно-ориентированных систем.
Перечислим основные типы объектов, применяемых в СУБД.
1. Объекты для работы с данными. Наиболее универсальным объектом
является текстовое поле TextBox. С его помощью можно отображать и
110
