Гринберг А.С., Иванюкович В.А., Новыш Б.В., Шешолко В.К. Ситуационный анализ и моделирование на основе информационных технологий баз данных

Подождите немного. Документ загружается.

Однако отношение, которое находится только в 1НФ, обладает структурой,

которая по некоторым причинам не совсем желательна. Например, очевидна

избыточность информации. Это приводит не только к увеличению размера базы

данных, но и к разным аномалиям обновления:

 Вставка (Insert). Нельзя вставить данные о поставщике (П5), не указав

деталь (Null-значение в ключевом поле недопустимо).

 Удаление (Delete). При удалении некоторого кортежа приходится удалять

слишком много другой информации (удаление информации о поставке

удаляет информацию о поставщике).

 Обновление (Update). Избыточная информация может привести к

несовместимым результатам. Если поставщик П1 переехал в другой город, а

обновление сделано не во всех кортежах, то база данных будет содержать

противоречивую информацию.

Для решения этой проблемы надо провести декомпозицию отношения.

Таблица находится во второй нормальной форме (2НФ), если она

удовлетворяет определению 1НФ и все ее поля, не входящие в первичный ключ,

связаны неприводимой зависимостью с первичным ключом (или находятся в

полной функциональной зависимости с первичным ключом).

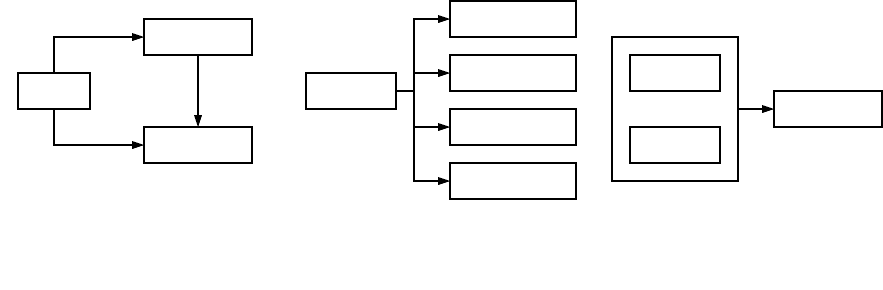
Функциональные зависимости отношений нашей базы данных,

приведенных ко 2НФ, показаны на рис.6.4.4, а соответствующие таблицы – на

рис.6.4.5.

Сейчас в базу данных можно вводить сведения и о поставщиках без

сведений об их товаре, при удалении сведений о товаре остаются остальные

Гор_П

П№

Статус

Д№

Имя_Д

Цв

Вес

Гор_Д

П№

Д№

Кол

Рис.6.4.4. Диаграмма функциональных зависимостей отношения,

приведенного к 2НФ

данные (о поставщиках, например), сведения о городе встречаются один раз и

это снимает проблему, связанную с избыточностью информации. Т.е.,

благодаря декомпозиции мы избавились от многих проблем, сопровождающих

отношения в 1НФ. В то же время, отношения, приведенные на рис.6.4.5, могут

быть объединены и тогда мы вернемся к отношению, изображенному на

рис.6.4.3 – значит декомпозиция проведена без потери данных.

Таким образом, первым этапом процедуры нормализации отношения

является создание проекций для исключения «приводимых» функциональных

зависимостей.

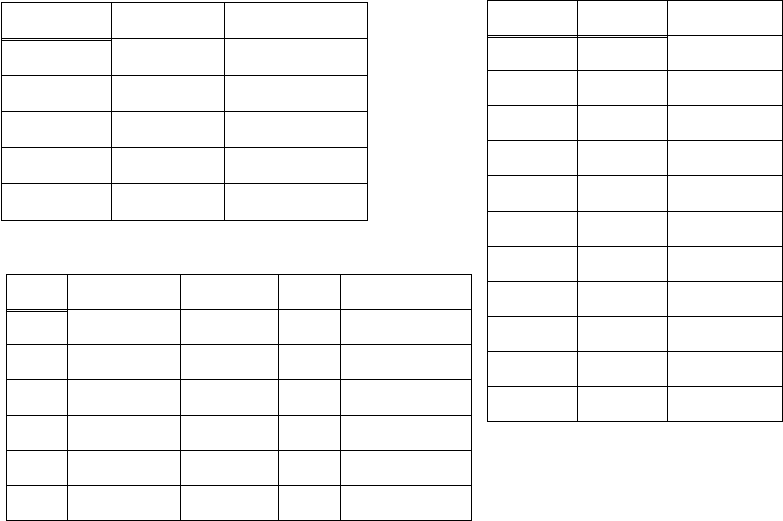
Рис.6.4.5.

Отношения в 2НФ

Однако структура отношений,

показанных на рис.6.4.5, может создать некоторые проблемы, связанные с

отношением Поставщик, в котором неключевые атрибуты не являются взаимно

независимыми. Зависимость атрибута Статус от атрибута П№ является

функциональной и неприводимой, но она также транзитивна через атрибут

Город – каждое значение П№ определяет значение Город, а каждое значение

Город определяет значение Статус. Но если выполняются зависимости АВ и

ВС, то выполняется также зависимость АС. Транзитивные зависимости

могут опять привести к аномалиям обновления:

 Вставка – нельзя включить данные о некотором городе и его статусе, пока в

нем нет поставщика.

П№ Статус Гор_П

П1 20 Брест

П2 10 Минск

П3 30 Гродно

П4 10 Минск

П5 20 Брест

П№ Д№ Кол

П1 Д1 300

П1 Д2 200

П1 Д3 400

П1 Д4 200

П1 Д5 100

П1 Д6 100

П2 Д1 300

П2 Д2 400

П3 Д2 200

П4 Д2 200

П4 Д4 300

Д№ Имя_Д Цв Вес Гор_Д

Д1 Тестер Черный 250 Борисов

Д2 Дозиметр Серый 700 Минск

Д3 Радиометр Черный 1400 Минск

Д4 Часы Желтый 140 Брест

Д5 Рулетка Красный 200 Пинск

Д6 Лом Черный 5000 Могилев

 Удаление – при удалении поставщика теряется информация о статусе

города (очевидно, что причиной такой проблемы является совместная

информация – в таблице содержится информация и о поставщиках, и о

городе).

 Обновление – статус городов повторяется несколько раз. При изменении

статуса города приходится просматривать множество строк, чтобы

исключить получение противоречивого результата, но вероятность ошибки

остается.

Проблема также решается декомпозицией отношения Поставщик:

Эта процедура исключает транзитивную зависимость и разрешает все

трудности.

Отношение находится в третьей нормальной форме (3НФ) тогда и

только тогда, когда оно находится в 2НФ и каждый неключевой атрибут

нетранзитивно зависит от первичного ключа

(или другими словами: таблица находится в третьей нормальной форме

(3НФ), если она находится в 2НФ и ни одно из ее неключевых полей не зависит

функционально от любого другого неключевого поля).

Таким образом, вторым этапом нормализации является создание

проекций для исключения транзитивных зависимостей.

В процессе выполнения процедуры нормализации часто возникают

ситуации, когда отношение может быть подвергнуто операции декомпозиции

несколькими способами. Например, отношение Поставщик (рис.6.4.5) с

функциональными зависимостями П№Город и ГородСтатус и,

следовательно, транзитивной зависимостью П№ Статус. Возможны варианты

декомпозиции этого отношения на две проекции, находящиеся в 3НФ:

А: (П№, Город) и (Город, Статус) (так было предложено ранее) и

В: (П№, Город) и (П№, Статус)

(третий вариант декомпозиции на проекции (П№, Статус) и (Город,

Статус) не может быть применен, поскольку выполняется с потерей

П№ Гор_П Гор_П Статус

информации – несколько городов могут иметь одинаковый статус, тогда будет

потеряна информация о городе, где находиться поставщик).

По некоторым причинам декомпозиция В менее желательна, чем

декомпозиция А. Например, после выполнения декомпозиции В невозможно

вставить информацию о том, что некоторый город имеет некоторый статус, без

указания поставщика из этого города.

В декомпозиции А обе проекции независимы друг от друга в том смысле,

что обновления в каждой из проекций могут быть выполнены совершенно

независимо друг от друга. В декомпозиции В обновление любой из двух

проекций должно контролироваться, чтобы не нарушить исходную зависимость

ГородСтатус. Т.е., проекции декомпозиции В не являются независимыми друг

от друга.

Концепция независимости проекций обеспечивает критерий выбора одной

из нескольких возможных декомпозиций. Проекции R1 и R2 отношения R

независимы в упомянутом выше смысле тогда и только тогда, когда

- каждая функциональная зависимость в отношении R является логическим

следствием функциональных зависимостей в проекциях R1 и R2;

- общие атрибуты проекций R1 и R2 образуют потенциальный ключ, по

крайней мере, для одной из них.

В рассматриваемом примере в декомпозиции А две проекции независимы,

поскольку их общий атрибут Город является потенциальным ключом для

второй проекции и каждая функциональная зависимость исходного отношения

находится в одной из проекций. Наоборот, в декомпозиции В две проекции не

являются независимыми, т.к. зависимость ГородСтатус не может быть

получена из функциональных зависимостей этих проекций, хотя их общий

атрибут П№ является потенциальным ключом для обеих проекций.

Идея нормализации с декомпозицией на независимые проекции

предложена Риссаненом (Rissanen) и называется декомпозицией с сохранением

зависимости.

6.5. Нормальная форма Бойса–Кодда

До сих пор мы предполагали для простоты, что каждое отношение имеет

только один потенциальный ключ – первичный ключ. Данное выше

определение 3НФ не совсем подходит, если

 отношение имеет два или более потенциальных ключа;

 два потенциальных ключа являются сложными и они перекрываются

(имеют хотя бы один общий атрибут).

Поэтому определение 3НФ было дополнено нормальной формой Бойса-

Кодда, НФБК (Boyce-Codd). Его можно сформулировать так:

Отношение находится в нормальной форме Бойса-Кодда тогда и только

тогда, когда детерминанты являются потенциальными ключами.

Другими словами, на диаграмме функциональных зависимостей стрелки

должны начинаться только с потенциальных ключей.

Комбинация таких условий не часто встречается на практике, поэтому для

отношений без таких условий 3НФ и НФБК эквиваленты.

Дадим еще одно определение: Таблица находится в нормальной форме

Бойса-Кодда (НФБК), тогда и только тогда, когда любая функциональная

зависимость между ее полями сводится к полной функциональной

зависимости от возможного ключа.

Рассмотрим пример, включающий два неперекрывающихся

потенциальных ключа:

Поставщик (П№, Имя_П, Статус, Город),

где атрибуты П№ и Имя_П являются потенциальными ключами, а атрибуты

Статус и Город совершенно независимы.

Диаграмма функциональных зависимостей

изображена на рис.6.5.1. Это отношение

находится в НФБК. Здесь все детерминанты

являются потенциальными ключами, а все

стрелки начинаются с потенциальных

ключей.

П№

Имя_П

Город

Статус

Рис.6.5.1. Диаграмма

отношения в НФБК

Приведем примеры отношений, в которых потенциальные ключи

перекрываются.

Первый пример:

Поставки (П№, Имя_П, Д№, Кол-во).

Потенциальными ключами здесь являются {П№, Д№} и {Имя_П, Д№}. Но

отношение не находится в НФБК, т.к. содержит два детерминанта, которые не

являются потенциальными ключами (П№ и Имя_П – детерминанты, поскольку

определяют друг друга). В этом отношении содержится некоторая

избыточность, которая обуславливает аномалии обновления. Для решения

проблемы отношение Поставки следует разбить на две проекции:

Поставщик (П№, Имя_П) и Поставки1 (П№, Д№, Кол-во).

Второй пример:

СДП (С, Д, П),

где атрибуты обозначают студента, предмет и преподавателя. Кортеж

отношения СДП означает, что некоторый студент С обучается некоторому

предмету Д у некоторого преподавателя П. При этом есть ограничения:

 Каждый студент изучает данный предмет у одного преподавателя;

 Каждый преподаватель ведет только один предмет (но каждый предмет

может преподаваться несколькими преподавателями).

Из первого ограничения следует зависимость {С,Д}П, из второго –ПД.

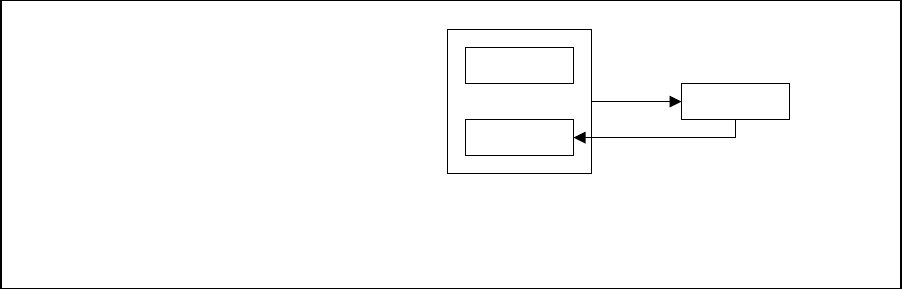
На рис.6.5.2 показан пример таблицы и диаграммы функциональных

зависимостей такого отношения. В рассматриваемом примере есть два

перекрывающихся потенциальных ключа – {С,Д} и {С,П}. Отношение находится

в 3НФ (присутствующая здесь транзитивная зависимость касается ключевого

СДПОлег МатемИльинОлегФизикаПетровПетрМатем Ильин ПетрФизикаИванов

Рис.6.5.2. Таблица и диаграмма функциональных зависимостей

для отношения СДП

атрибута), но не находится в НФБК и характеризуется некоторыми аномалиями

обновления. Например, если удалить информацию о том, что Олег изучает

физику, то мы потеряем информацию о том, что Петров преподает физику. Эта

проблема вызвана тем, что П является детерминантом, но не является

потенциальным ключом. Для решения этой проблемы исходное отношение

надо разбить на две проекции: СП и ПД.

Таким образом, концепция НФБК позволяет избавиться от некоторых

проблем, присущих отношениям в 3НФ. Более того, определение НФБК проще

определения 3НФ, т.к. в нем не используются понятия 1НФ, 2НФ, первичного

ключа и транзитивной зависимости. Кроме того, понятие потенциального

ключа может быть заменено введением более фундаментального понятия

функциональной зависимости. Но с другой стороны, концепции первичного

ключа, транзитивной зависимости и т.д. полезны на практике, поскольку

позволяют представить идею постепенного процесса, выполняемого

разработчиком для приведения произвольного отношения к эквивалентному

набору отношений в НФБК.

6.6. Нормальные формы, обоснованные более сложными зависимостями

В следующих нормальных формах (4НФ и 5НФ) учитываются не только

функциональные, но и многозначные зависимости и зависимости соединения

между полями таблицы. Для знакомства с ними рассмотрим

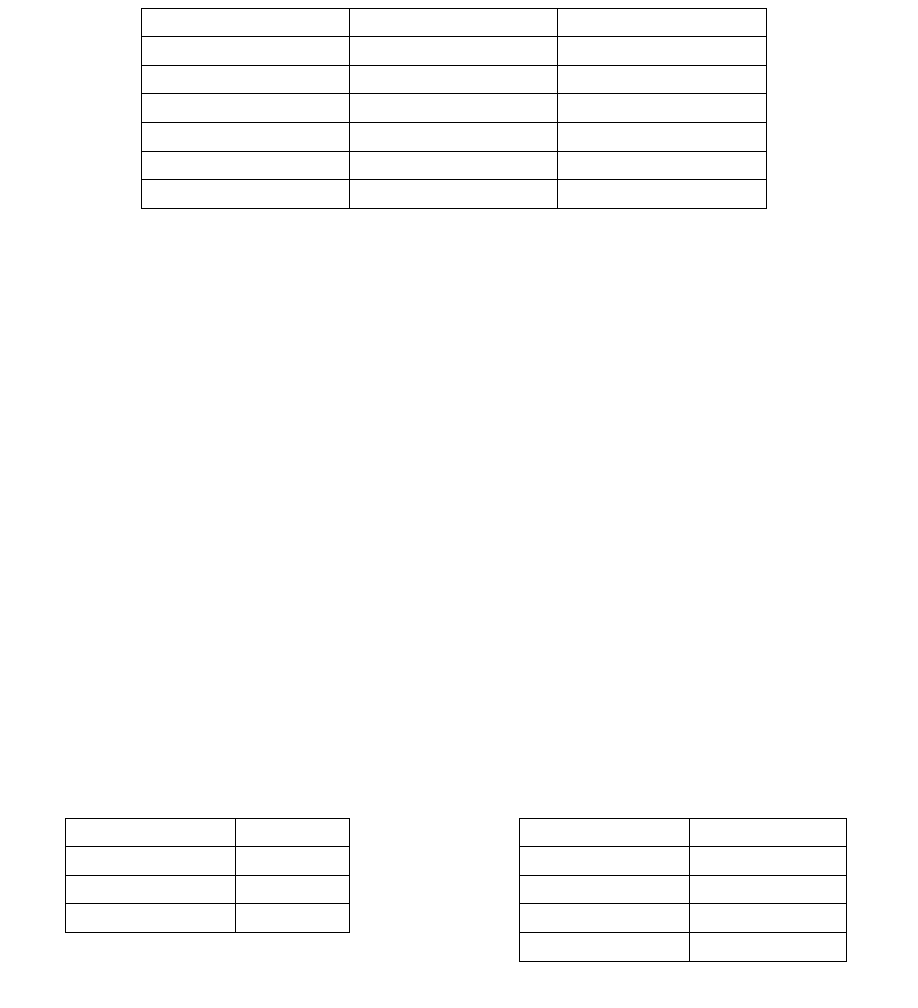
ненормализованное отношение, показанное на рис.6.6.1. Каждый кортеж

отношения содержит название курса, группу имен преподавателей, и набор

учебников. Это значит, что каждый курс может преподаваться любым

преподавателем с использованием любых учебников. Преобразуем это

отношение в эквивалентное нормализованное. Для представленных данных

функциональные зависимости не определены. Поэтому нет формальной основы

Д П У

Физика Петров Механика

Иванов Оптика

Математика Иванов Геометрия

Мат. анализ

Рис.6.6.1. Ненормализованное отношение ДПУ

для декомпозиции этого отношения и нормализованное отношение изображено

на рис.6.6.2.

Очевидно, что отношение ДПУ характеризуется значительной

избыточностью и приводит к возникновению аномалий обновления. Тем не

менее, отношение является полностью ключевым и поэтому находится в НФБК.

Возникающие проблемы вызваны тем, что преподаватели и учебники

полностью независимы друг от друга. Проблема нормализованного отношения

ДПУ не возникла бы, если бы при нормализации некоторых

ненормализованных отношений были разделены все независимые

повторяющиеся группы. В нашем случае можно было улучшить ситуацию,

заменив отношение ДПУ проекциями {Д,П} и {Д,У} (рис.6.6.3). При этом обе

проекции являются полностью ключевыми и находятся в НФБК. Такая

декомпозиция не может быть выполнена на основе функциональных

зависимостей, которых нет в этом примере. Ее можно осуществить на основе

многозначной зависимости. Многозначные зависимости – это обобщение

функциональных зависимостей в том смысле, что каждая функциональная

зависимость является многозначной, но не наоборот.

В отношении ДПУ есть две многозначные зависимости: ДП и ДУ.

Д П У

Физика Петров Механика

Физика Петров Оптика

Физика Иванов Механика

Физика Иванов Оптика

Математика Иванов Геометрия

Математика Иванов Мат. анализ

Рис.6.6.2. Нормализованное отношение ДПУ

Д П Д У

Физика Петров Физика Механика

Физика Иванов Физика Оптика

Математика Ильин Математика Геометрия

Математика Мат. анализ

Рис.6.6.3. Проекции {Д,П} и {Д,У} отношения ДПУ

Первая из этих многозначных зависимостей означает, что хотя для каждой

дисциплины не существует одного соответствующего только этой дисциплине

преподавателя, т.е. не выполняется функциональная зависимость ДП, тем не

менее, каждая дисциплина имеет определенное множество преподавателей,

независимо от наименования учебника.

Вторая многозначная зависимость интерпретируется аналогично.

Пусть А,В,С являются произвольными подмножествами множества

атрибутов отношения R. Тогда В многозначно зависит от А (А



В) тогда и

только тогда, когда множество значений В, соответствующее заданной паре

значений (А,С) отношения R, зависит только от А, но не зависит от С.

Очевидно, что многозначная зависимость АВ выполняется только

тогда, когда выполняется многозначная зависимость АС. Многозначные

зависимости всегда образуют связанные пары.

Возвращаясь к проблемам отношения ДПУ, можно сказать, что они

связаны с существованием многозначных зависимостей, которые не являются

функциональными (именно наличие таких зависимостей требует вставлять два

кортежа, когда надо добавить данные еще об одном преподавателе физики).

Проекции {Д,П} и {Д,У} не содержат многозначных зависимостей и поэтому

являются более желательными. Прежде чем дать определение четвертой

нормальной формы, познакомимся с теоремой Фейгина (R. Fagin):

Пусть А,В,С являются множествами атрибутов отношения R{А,В,С}.

Отношение R будет равно соединению его проекций {А,В} и {А,С} тогда и

только тогда, когда для отношения R выполняются многозначные зависимости

АВ и АС.

Отношение R находится в четвертой нормальной форме (4НФ) тогда и

только тогда, когда в случае существования многозначной зависимости



B все остальные атрибуты R функционально зависят от A.

Другими словами:

Отношение R находится в 4НФ, если оно находится в НФБК и все

многозначные зависимости отношения R фактически являются

функциональными зависимостями от потенциальных ключей.

Отношение ДПУ не находится в 4НФ, поскольку содержит многозначную

зависимость, не являющуюся функциональной зависимостью. Однако обе

проекции {Д,П} и {Д,У} находятся в 4НФ, которая по сравнению с НФБК

позволяет создать улучшенную структуру.

Во всех рассмотренных до этого момента процедурах нормализации

производилась декомпозиция одного отношения в два. Иногда это сделать не

удается, но возможна декомпозиция в большее число отношений, каждое из

которых обладает лучшими свойствами. Такое отношение называется n-

декомпозируемым отношением, для которого n>2.

Рассмотрим, например, отношение Поставщики-Детали-Проекты

(рис.6.6.4). Предположим, что один и тот же поставщик может поставлять

несколько типов деталей для разных проектов. Первичным ключом этого

отношения является полная совокупность его атрибутов, отсутствуют

функциональные и многозначные зависимости (многозначной зависимости нет,

т.к. для П1 набор деталей зависит от проекта). Поэтому отношение находится в

4НФ. Однако в нем могут существовать аномалии (не всегда очевидные),

которые можно устранить путем декомпозиции в три отношения. Такая

декомпозиция возможна без потерь информации только в случае

существования зависимости соединения.

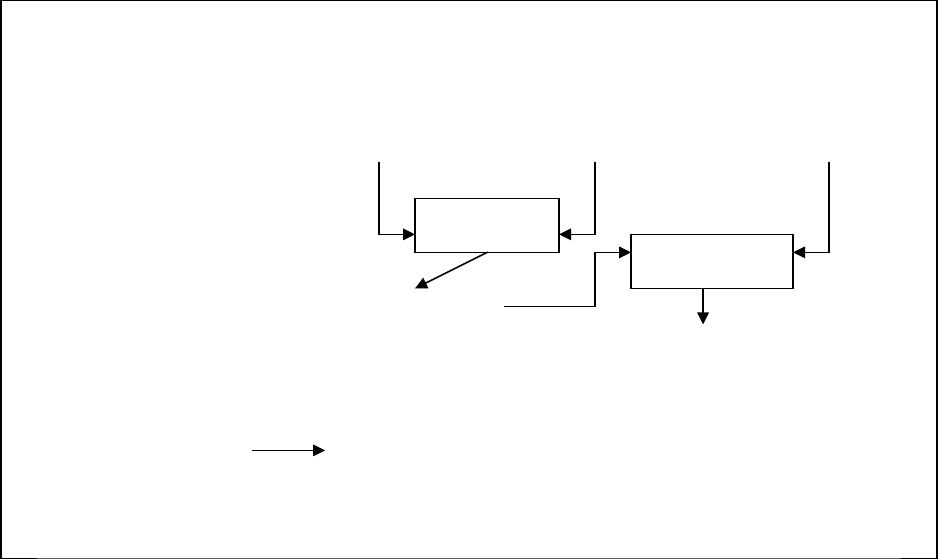
ПДПрПДДПрПрППДПрПДППрПрПП1Д1Пр2П1Д1Д1Пр2Пр2П1П1Д2Пр1П1Д2Д2Пр1

Пр1П1П2Д1Пр1 П2Д1Д1Пр1 Пр1 П2П1Д1Пр1

ПДПрПДПрПДПр

(исходн)П1Д1Пр2ПДПрП1Д2Пр1П1Д1Пр2П2Д1

Пр1 П1Д2Пр1П2Д1Пр2П2Д1Пр1

П1Д1Пр1П1Д1Пр1

Соединение по

атрибуту Д

Соединение по

атрибутам Пр и П

Лишний кортеж

Рис.6.6.4. Пример 3-декомпозиции отношения ПДПр

100