Грин В.М. Учебное пособие - Основы инженерного эксперимента
Подождите немного. Документ загружается.

21
3.2 Дисперсионный анализ
Напомним, что при дисперсионном анализе имеется один или несколько управ-
ляемых факторов и одна функция отклика. Необходимо установить, значимо ли (в стати-
стическом смысле) влияние каждого фактора на функцию отклика, и упорядочить факторы
(если их несколько) по степени влияния на функцию отклика.
Вспомним пример 2 из главы 1.
Необходимо оценить влияние
шагов в трубном пучке S
1
и S
2
на интенсивность те-
плообмена (значение критерия Нуссельта Nu).
Основная идея дисперсионного анализа заключается в следующем. Величина откли-
ка
Y
ij
в каждой точке (
X
1i
,X
2j
) есть сумма некоторой средней величины
µ,
отклонений
β
i
и
γ
j
, вызванных отдельными факторами, их взаимодействиями
δ
ij
и случайными отклоне-
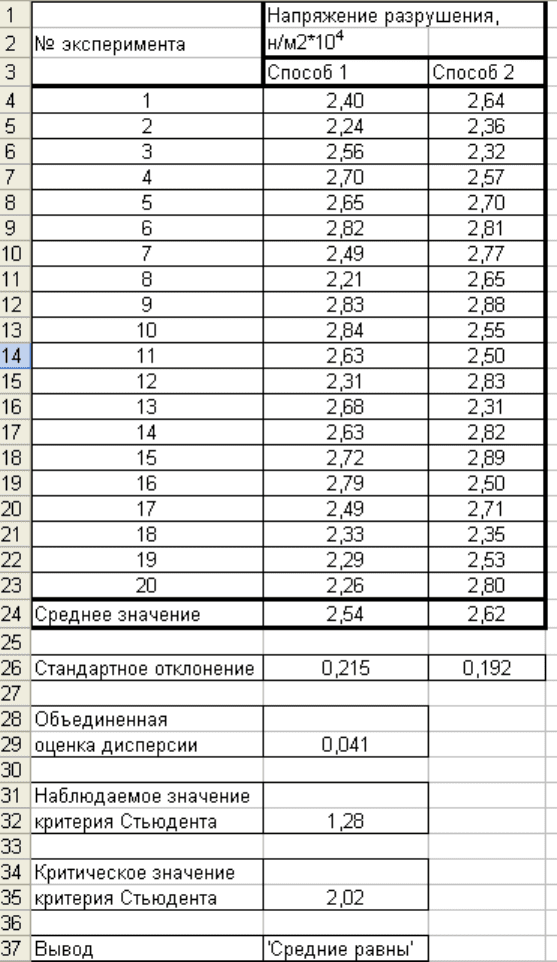
ниями
Z
, вызванными неконтролируемыми факторами:
22
Y
ij=
µ+ β
i
+ γ
j
+
δ
ij
+ Z.
Если упростить задачу, предположив, что эффекты взаимодействия отсутствуют
(необходим предварительный анализ), отклонения, вызванные факторами, имеют одинако-
вые дисперсии, случайные отклонения
Z
распределены по нормальному закону, модель ре-
зультатов наблюдения упрощается, можно проводить статистический анализ:
Y
ij=
µ+ β
i
+ γ
j
+ Z.
Переходим к построению матрицы условий эксперимента. Выберем по 4 уровня для
факторов S
1
и S
2
:
S
1
=(2d, 2,5d, 3d, 3,5d),
S
2
=(1,5d, 2d, 2,5d, 3d),
где
d
– диаметр трубы.
Полный факторный план включает n=4х4=16 экспериментов:
Номер опыта Значение S
1
Значение S
2
Отклик Nu
1 S
11
S
21
Nu
11
2 S
11
S
22
Nu
12
3 S
11
S
23
Nu
13
4 S
11
S
24
Nu
14
5 S
12
S
21
Nu
21
6 S
12
S
22
Nu
22
7 S
12
S
23
Nu
23
8 S
12
S
24
Nu
24
9 S
13
S
21
Nu
31
10 S
13
S
22
Nu
32
11 S
13
S
23
Nu
33
12 S
13
S
24
Nu
34
13 S
14
S
21
Nu
41
14 S
14
S
22
Nu
42
15 S
14
S
23
Nu
43
16 S
14
S
24
Nu
44
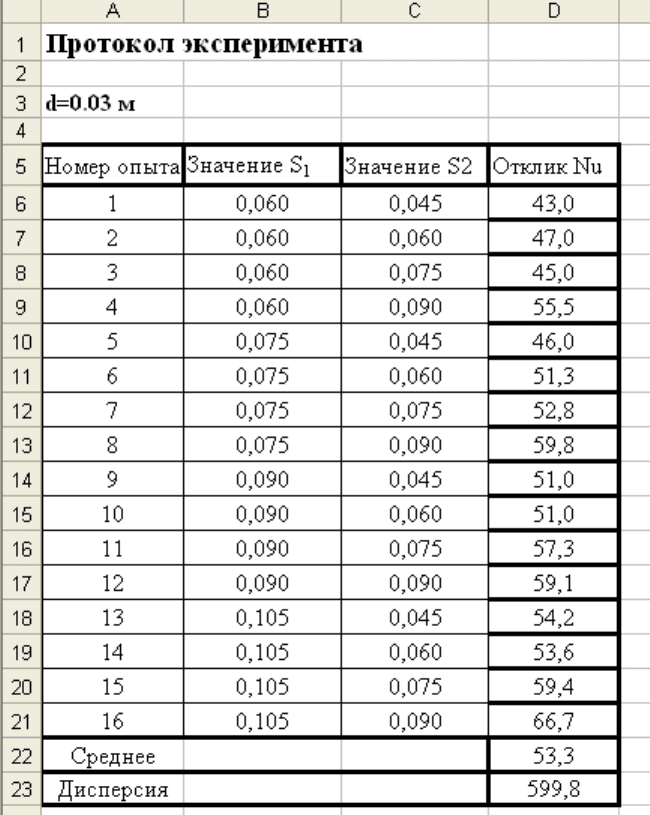
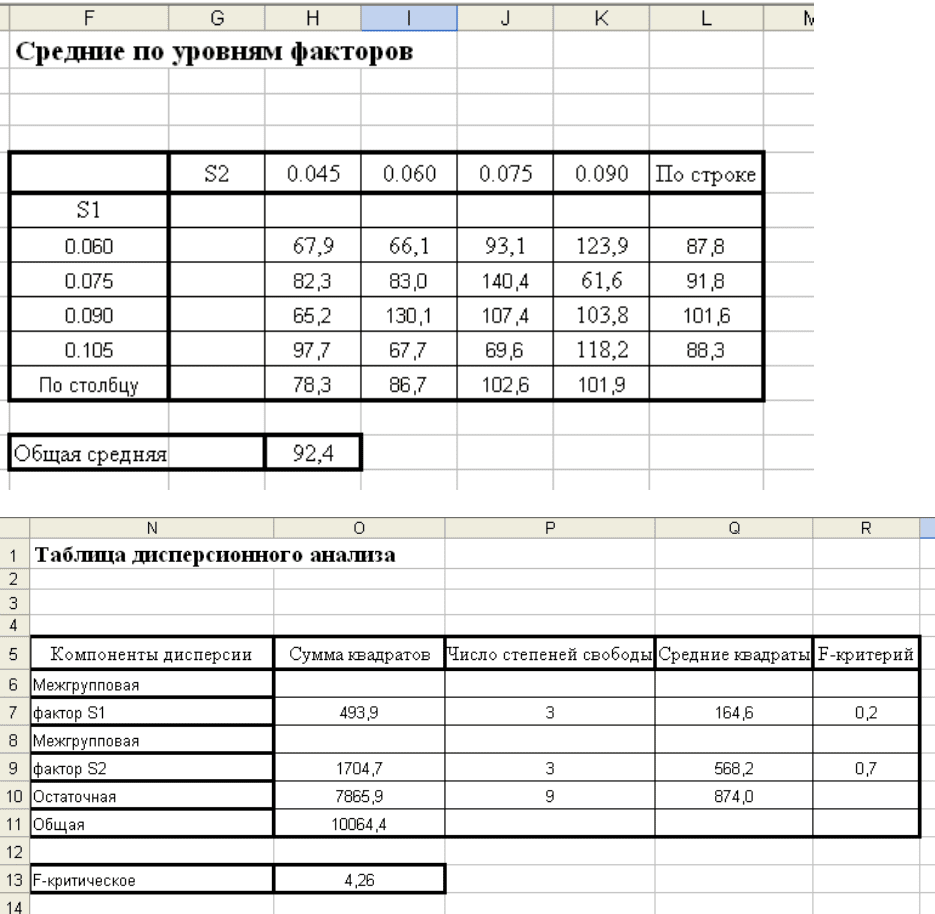
Проводим эксперимент, результаты заносим в протокол.
23
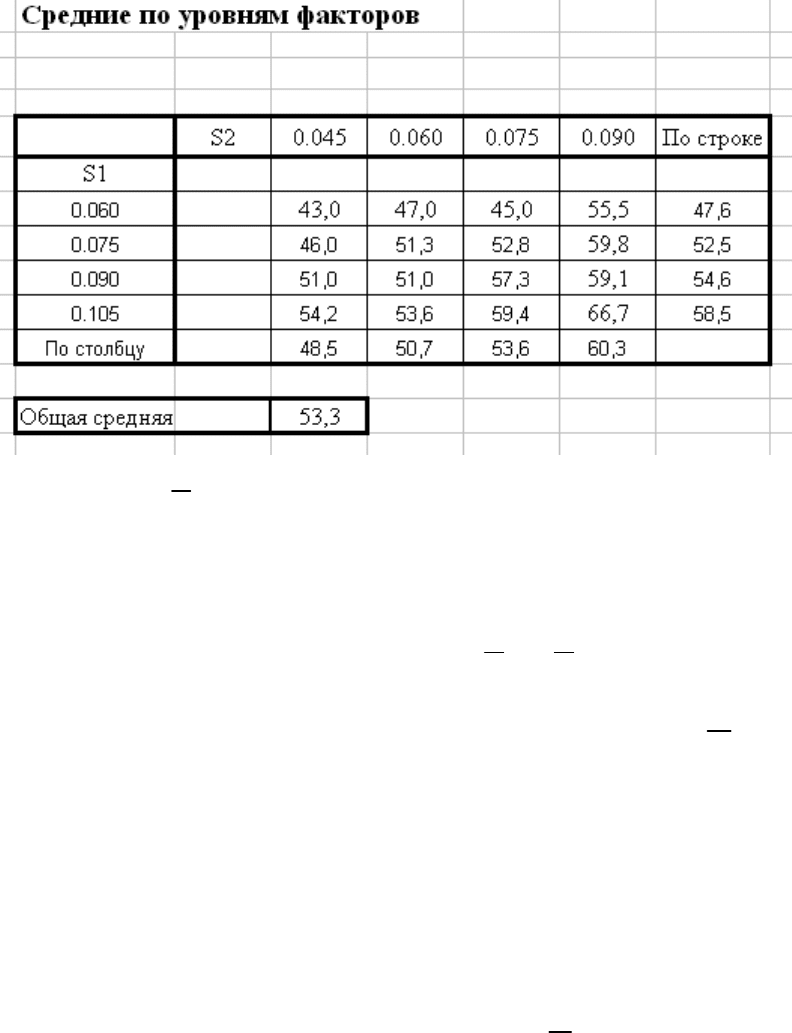
Суммируем значения откликов по уровням факторов и находим средние по строкам
и столбцам.
24
Общая средняя
3,53=Y
.
Составляем таблицу дисперсионного анализа.
Суммы квадратов отклонений, вызванные влиянием j-го фактора, вычисляем по
формуле:
2
1
2
)(()(
∑
=
−=
r
i
ijj
YYXS
,
где i – номер уровня, j – номер фактора, r – число уровней (r=4),
ij
Y
- средние по
строкам и столбцам.
4,246))3,535,58()3,536,54()3,535,52()3,536,47(()(
2222
1
2
=−+−+−+−=XS
5,313))3,533,60()3,536,53()3,537,50()3,535,48(()(
2222
2
2
=−+−+−+−=XS
.
Общая сумма квадратов отклонений вычисляется по формуле:
∑∑
==
−=
k
j
r
i
ij
YYS
11
22
)(
,
где k – количество факторов (k=2).
S
2
=599,8.
Остаточная сумма квадратов отклонений, обусловленная случайными факторами,
равна
8,39)()(
2
2
1
222
0
=−−= XSXSSS
.

25
Вычисляем средние квадраты
1
)(
1
2
2
1
−
=
r
XS
s
,
1
)(
2
2
2
2
−
=
r
XS
s
,
)1)(1(
2
0
2
0
−−
=
rr
S
s
.
1,82
3
4,246
2
1
==s
,
5,104
3
5,313
2
2
==s
,
4,4
9
8,39
2
0
==s
.
Вычисляем наблюдаемое значение критерия Фишера-Снедекора:
2
0
2
1
1
s
s
F =
,
2
0
2
2
2
s
s
F =
.
6,18
4,4
1,82
1
==F
,
6,23
4,4
5,104
2
==F
.
Наконец, по таблицам распределения Фишера-Снедекора (приложение Б) для веро-
ятности ошибки
α=
0,05, числа факторов
k
=2, числа степеней свободы
(r-1)(r-1)=
9 нахо-
дим
Fкр
=4,26.
Результаты сводим в таблицу.
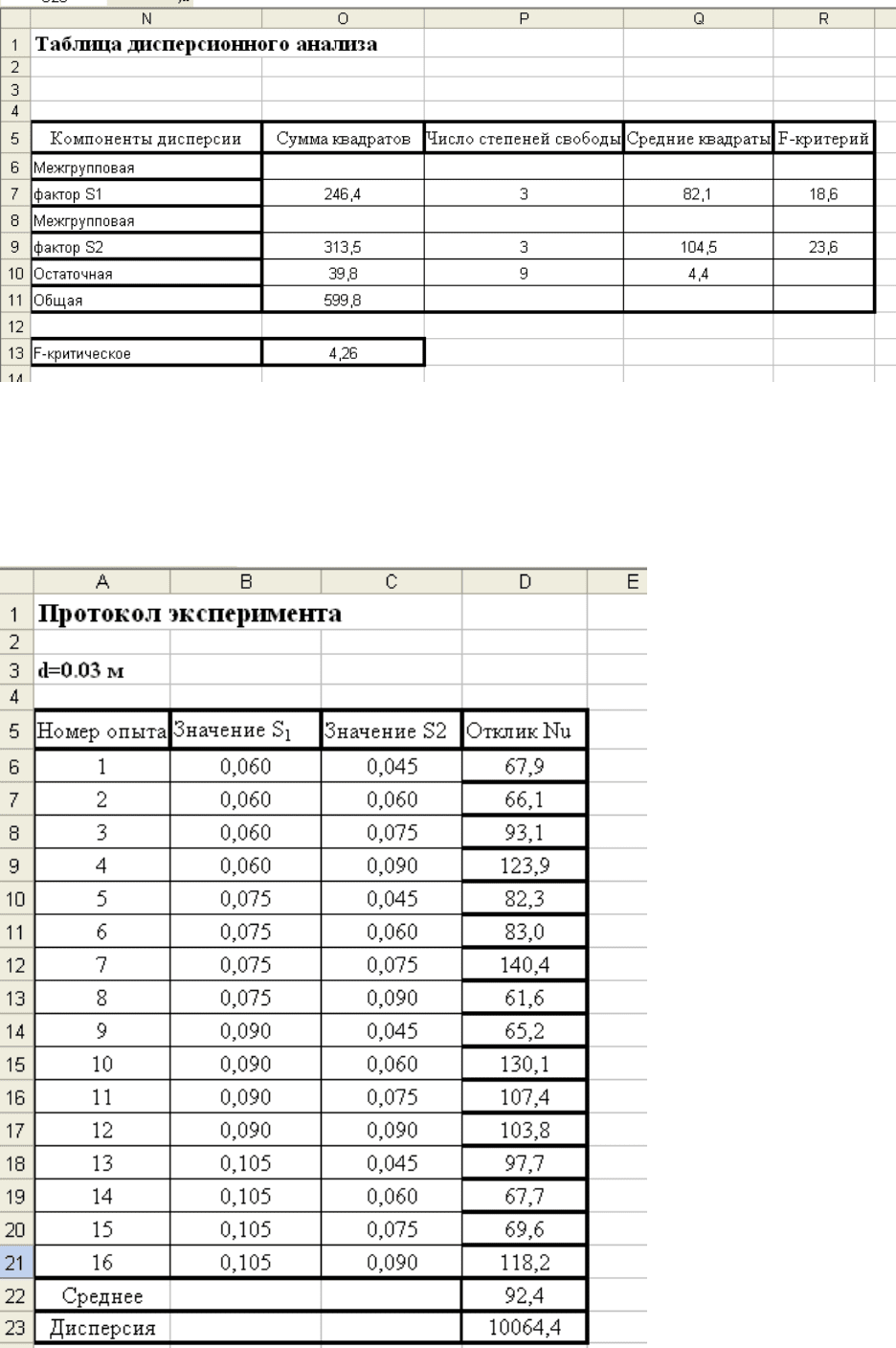
26
Поскольку наблюдаемое значение для первого и второго факторов больше крити-
ческого, следует признать оба фактора значимыми, причем фактор S2 оказывает на отклик
несколько большее влияние.
В следующем примере, наоборот, следует признать влияние факторов незначимым.
27
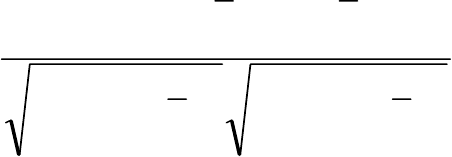
28
3.3 Регрессионный анализ
Итак, при регрессионном анализе ставится задача на основе данных эксперимента оты-
скания функциональной зависимости математического ожидания отклика M(Y) от значе-
ний одного или нескольких факторов:
M(Y)=f(X1) или M(Y)=f(X1,X2) и т.д.
Этот этап начинают, как правило, с линейного регрессионного анализа. Предполагает-
ся, что наблюдаемое в опыте значение отклика Y можно мысленно разделить на две части:
одна из них закономерно зависит от X, то есть является функцией X, другая часть – слу-
чайна по отношению к X. Отклик можно представить в виде
ε
+
=
)(XfY
,
где
ε
- некоторая случайная величина. Иногда
ε
называют ошибкой эксперимен-
та, связывая ее присутствие с несовершенством метода измерения Y. Возникает задача об
отыскании функции отклика
f(X).
Класс функций, в котором ищется функция
f(X),
часто
определяется физической сущностью происходящих процессов. Это могут быть экспонен-
ты, степенные функции, но начинают подбор и анализ, как правило, с линейной функции
bxaXf
+
=
)(
.
Прежде чем переходить к определению коэффициентов
a
и
b
, проводят вычисление
коэффициента корреляции, величина которого позволяет судить об обоснованности приня-
тия линейной модели.
Коэффициентом корреляции называют величину
∑∑
∑
==
=
−−
−−
=
n
i
i
n
i
i
n
i
ii
yyxx
yyxx
r
1
2
1
2
1
)()(
))((
.
Коэффициент корреляции принимает значения в интервале [-1,1]. Чем больше
абсолютная величина коэффициента корреляции, тем с большим основанием можно
предполагать наличие линейной зависимости между переменными. В этом случае можно
переходить к определению коэффициентов линейной зависимости, например, методом
наименьших квадратов. В пакете Microsoft Excel функции вычисления коэффициента кор-
реляции и построения линейной регрессии являются встроенными.
Если предполагается нелинейная зависимость
Y
от
X
, то с помощью преобразова-
ний нередко удается привести зависимость к линейной и воспользоваться далее инструмен-
тами определения коэффициентов в линейном уравнении регрессии.
Например, при экспериментальном исследовании процессов теплообмена [2] ищут
зависимость величины критерия Нуссельта от величины критерия Рейнольдса в виде:
n
cNu Re=
.
Проведя логарифмирование выражения
Relglglg ncNu
+
=
29
и обозначив
Y=lg Nu, A=lg c, X=lg Re
, ,приходим к установлению линейной зави-
симости вида
nXAY
+
=
.
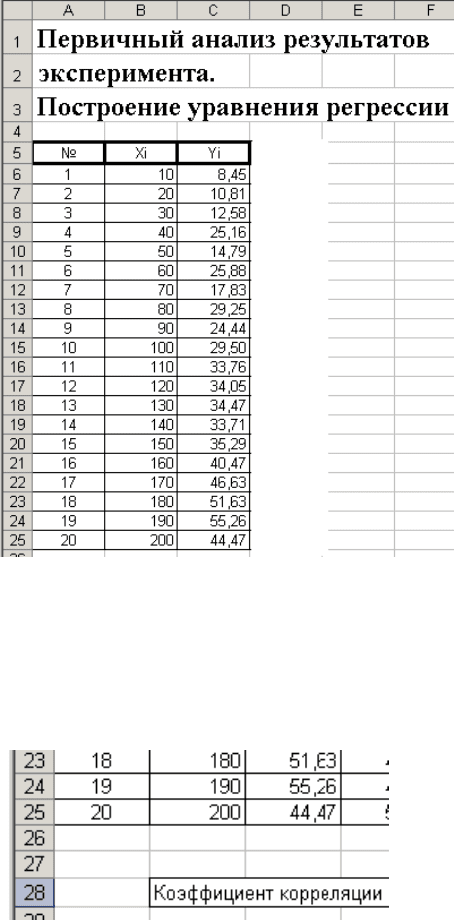
Пусть имеются результаты 20 измерений независимой переменной X и зависимой
переменной Y. Открываем электронные таблицы EXCEL, в верхней части листа
формируем заголовок, в ячейки A5 – C25 заносим таблицу.
Вычислим коэффициент корреляции между переменными X и Y. Для этого в ячейку
B28 сначала занесем текст «Коэффициент корреляции».
Затем в
ячейку E28 через главное меню «Вставка – Функция – Статистические»
вставим функцию КОРРЕЛ.
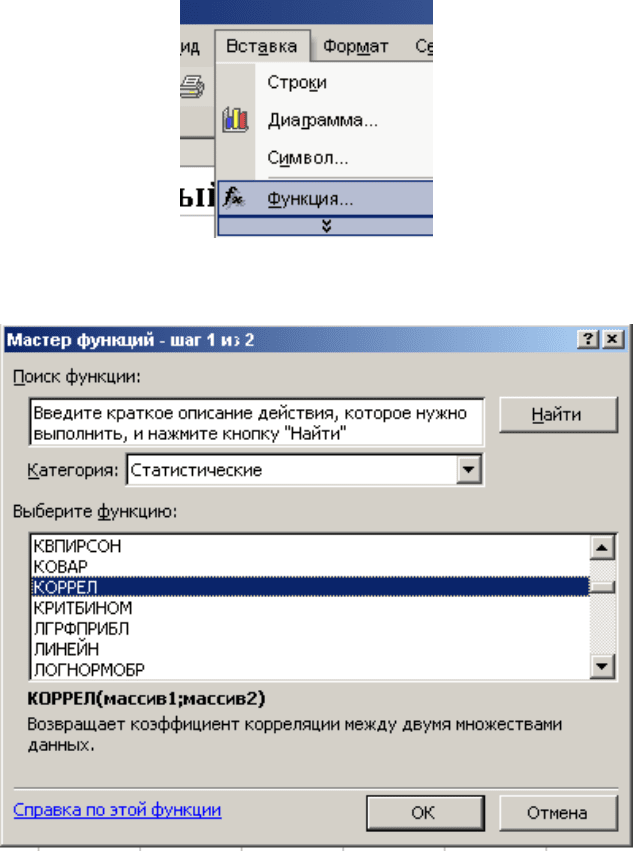
30
Для заполнения окна «Массив1» выделим столбец значений X, а окна «Массив2» -
столбец значений Y.
