Григорьева Е.В., Дымков М.П. Высшая математика. Второй семестр
Подождите немного. Документ загружается.

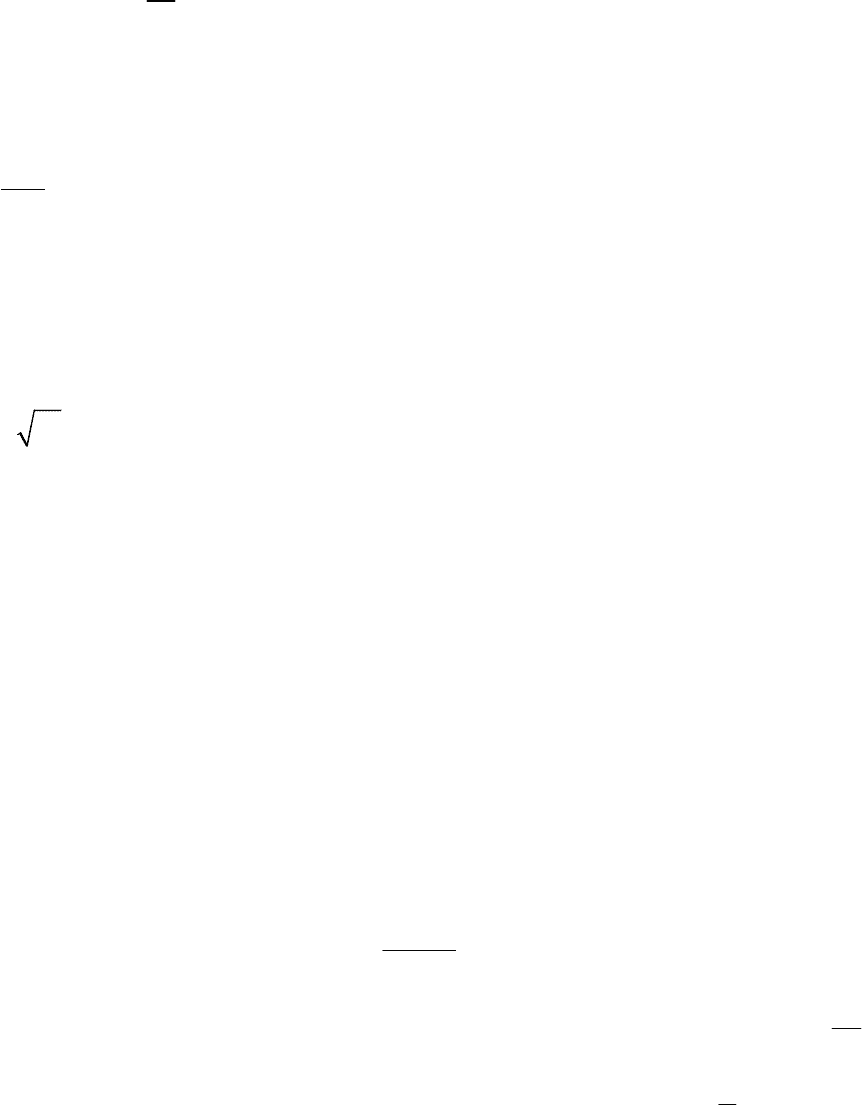
следует сходимость ряда , а из расходимости ряда следует
расходимость ряда . Иначе говоря,
если «больший» ряд сходится, то и
«меньший» ряд сходится; если «меньший» ряд расходится, то и «больший»
ряд расходится.
1
n
n
a
∞
=
∑
1
n
n
a
∞
=
∑
1
n
n
b
∞
=
∑
Второй признак сравнения. Если существует конечный, отличный от
нуля, предел
lim , 0, ,
n
n
n
a
LL L
b
→∞
=≠≠∞ то ряды
1
n
n
a
∞
=
∑
и сходятся или
расходятся одновременно.
1
n
n
b
∞
=
∑
Признак Даламбера. Если для ряда существует предел
,
1
0,
nn
n
aa
∞
=
>
∑
1
lim ,
n
n
n
a
l
a
+
→∞
= то при ряд сходится, при ряд расходится, при
1l < 1l > 1l
=
вопрос остается открытым ― нужно применять другие признаки.
Признак Даламбера удобно применять в тех случаях, когда в записи
общего члена ряда участвуют факториалы (!) и степени.
Признак Коши. Если для ряда существует предел
1
,
nn
n
aa
∞
=
>
∑
0,
lim
n
n
n
l
→∞
= a
, то при ряд сходится, при ряд расходится, а при
1l < 1l > 1l
=
вопрос остается открытым.
Интегральный признак. Если члены ряда не
возрастают и существует функция
,
1
0,
nn
n
aa
∞
=
>
∑
123
... ...
n
aaa a≥≥≥≥≥
()
f
x
, которая
определена на промежутке
)
1;
+
∞⎡
⎣
, непрерывна, не возрастает и
то для сходимости ряда
( ), 1,2,...,
n
afnn==
1
n
n
a
∞
=
∑
необходимо и
достаточно, чтобы несобственный интеграл
1
()
f
xdx
∞
∫
сходился.
Тема «Признаки сходимости знакоположительных рядов»
Пример. Исследовать ряд
2
1
2
12
n
n
n
∞
=
+
∑
на сходимость.
Решение. Сравним данный ряд с геометрическим рядом
1
1
2
n
n
∞
=
∑
,
который сходится как геометрический ряд со знаменателем
1
1
2
q =<
. Имеем
51
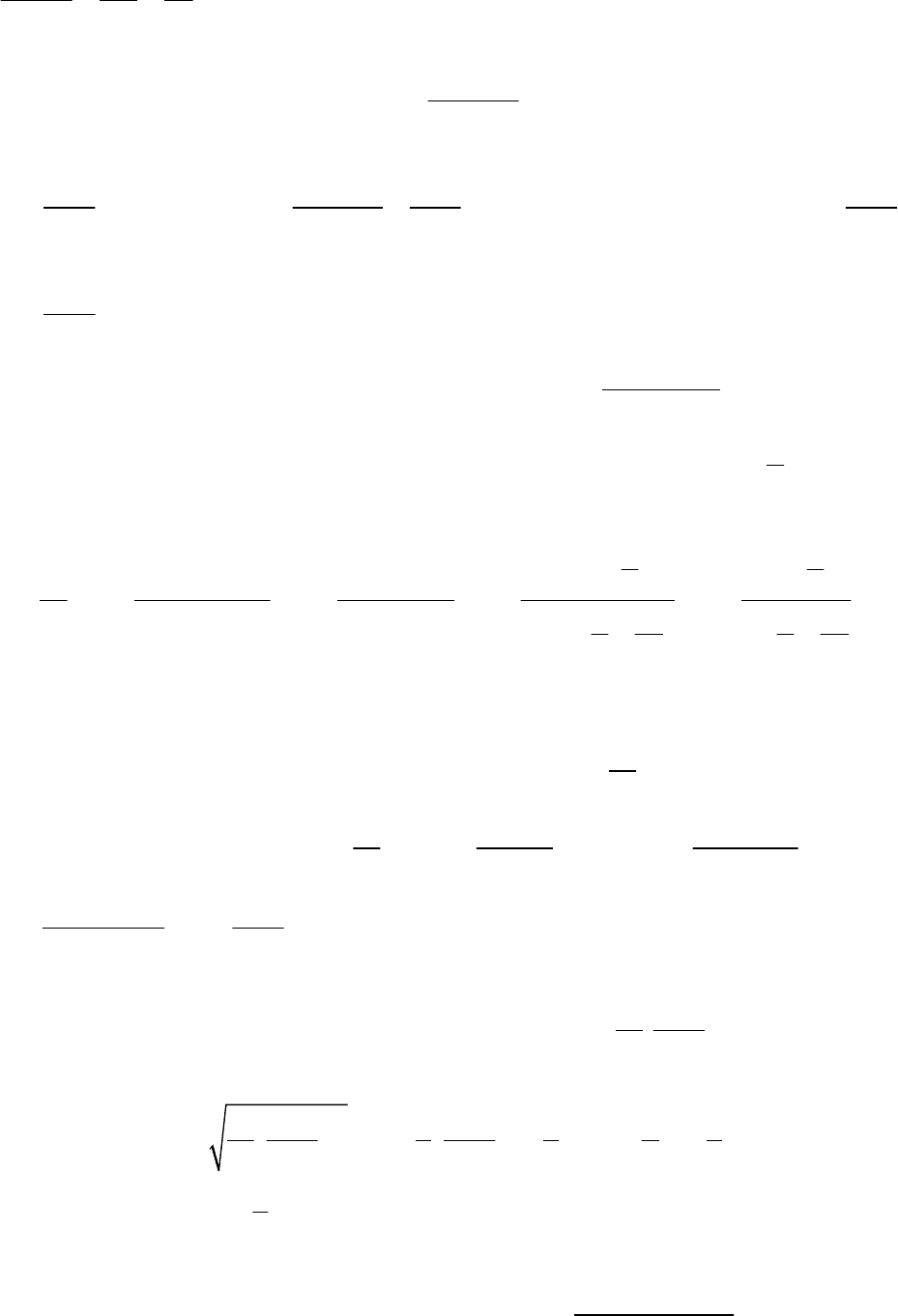
2
2
12
n
n
<
+
2
2
22
n
n
=
1
n
для всех , значит, на основании первого признака
сравнения ряд сходится.
n
Пример. Исследовать ряд
1
1
ln( 1)
n
n
∞
=
+
∑
на сходимость.
Решение. Сравним данный ряд с расходящимся гармоническим рядом
1
1
1
n
n
∞
=
+
∑
. Поскольку
11
ln( 1) 1nn
>
+
+
и гармонический ряд
1
1
1
n
n
∞
=
+
∑
расходится, то на основании первого признака сравнения заключаем, что ряд
1
1
1
n
n
∞
=
+
∑
расходится.
Пример. Исследовать на сходимость ряд
2
1
21
35
n
n
nn
∞
=
−
−
+
∑
.
Решение. Сравним данный ряд с гармоническим рядом
1
1
n
n
∞
=
∑
, который
расходится. Имеем
lim
n
n
n
a
b
→∞
=
2
(2 1)
lim
(35)
n
nn
nn
→∞
−
=
−+
2
2
2
lim
35
n
nn
nn
→∞
−
=
−+
2
2
2
1
(2 )
lim
35
(1 )
n
n
n
n
nn
→∞
−
=
−+
2
1
2
lim 2
35
1
n
n
nn
→∞
−
=
−+
.
Поскольку то на основании второго признака сравнения заключаем,
что исследуемый ряд расходится.
20,≠
Пример. Исследовать на сходимость ряд
1
!
5
n
n
n
∞
=
∑
.
Решение. Так как
!
,
5
n
n
n
a =
1
1
(1)!
,
5
n
n
n
a
+
+
+
= то
lim
n
l
→∞
=
1
(1)!5
5!
n
n
n
n
+
+
=
lim
n→∞
!( 1) 5
55 !
n
n
nn
n
+
=
⋅⋅
1
lim
5
n
n
→∞
+
=∞
. Так как
1,
∞
>
то исследуемый ряд
расходится.
Пример. Исследовать на сходимость ряд
2
1
11
()
3
n
n
n
n
n
∞
=
+
∑
.
Решение. Применим признак Коши, для чего найдем
2
11
lim ( )
3
n
n
n
n
n
n
→∞
+
=
11
lim ( )
3
n
n
n
n
→∞
+
=
11
lim(1 )
33
n
n
e
n
→∞
+
= .
Так как и
2,72e ≈
1,
3
e
< то на основании признака Коши заключаем, что
исследуемый ряд сходится.
Пример. Исследовать сходимость ряда
1
1
(1)ln(1
n
nn
∞
=
)
+
+
∑
.
52
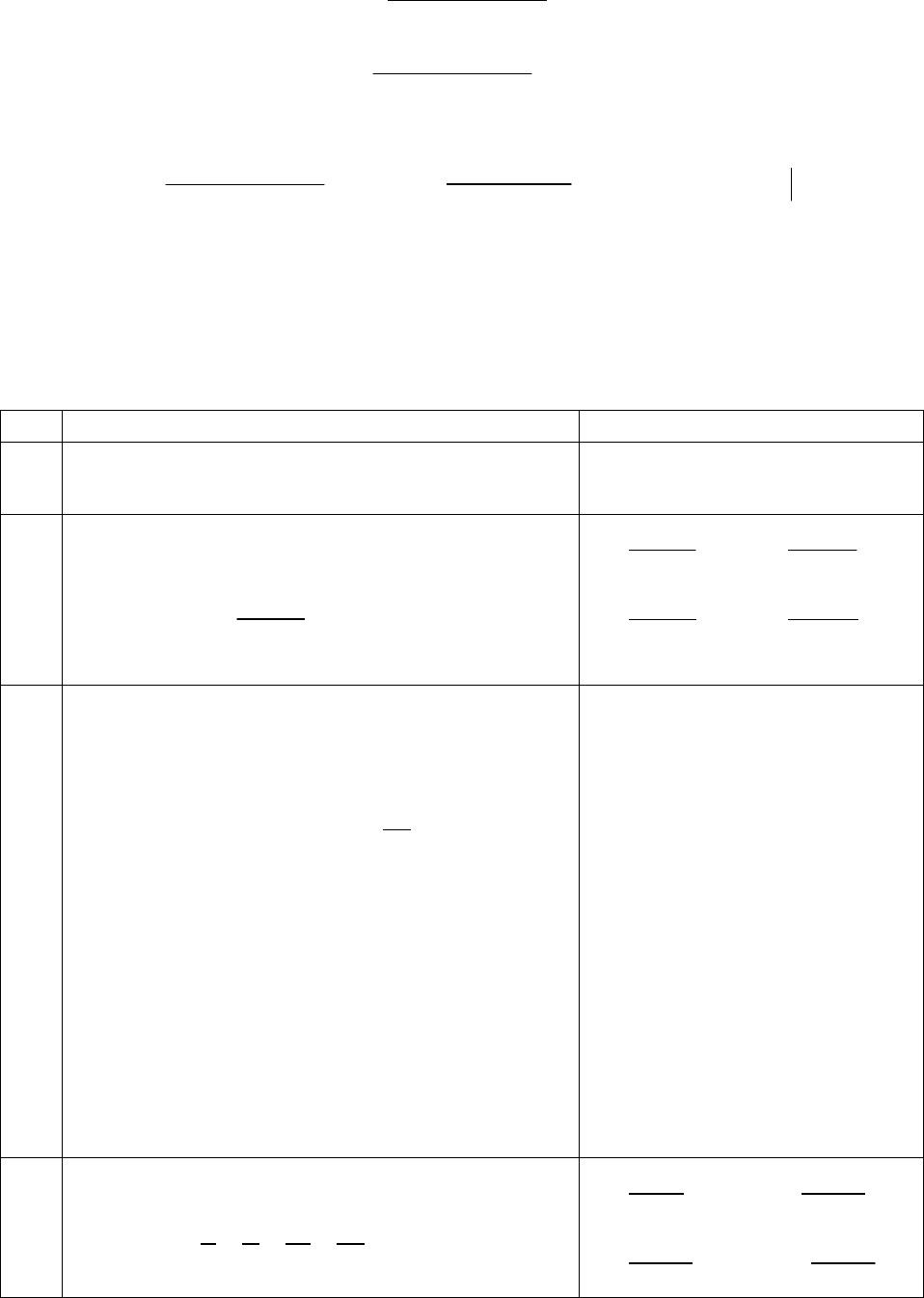
Решение. Применим интегральный признак Коши-Маклорена. Заменяя
в формуле общего члена
1
(1)ln(1
n
a
nn
=
)
+
+
число на переменную
n
x
,
получаем функцию
1
()
(1)ln(1
fx
xx
=
)
+
+
. Вычисляем несобственный
интеграл
1
()
f
xdx
∞
∫
=
1
∞
∫
1
(1)ln(1)
dx
xx
=
++
1
(ln( 1))
lim
ln( 1)
B
B
dx
x
→+∞
+
=
+
∫
1
lim ln(ln( 1))
B
B
x
→+∞
+=
= .
lim (ln(ln ) ln(ln 2))
B
B
→+∞
−=∞
Интеграл расходится, и следовательно, исходный числовой ряд также
расходится.
Задачи для самостоятельного решения
№ Задание Варианты ответов
1.
Если
n-й член числового ряда
, то сумма
1
(1) (3 2)
n
n
an
−
=− +
4
aa
5
+
равна
1) 2; 2) 3; 3) –31 ;
4) 32; 5) другой ответ.
2.
Найти
(1)n
+
-й член
1n
a
+
ряда, n-й член
которого
32
21
n
n
a
n
+
=
−
.
1)
3
2
n
n
+ 3
; 2)
3
21
n
n
4
+
+
;
3)
3
21
n
n
+
+
5
; 4)
36
22
n
n
+
+
;
5) другой ответ.
3.
Пусть и
1
n
n
a
∞
=
∑
1
n
n
b
∞
=
−
∑
ряды с
положительными членами. Известно, что
ряд сходится и
1
n
n
a
∞
=
∑
lim
n
n
n
a
l
b
→∞
=
. Укажите
верные утверждения:
а) если , то вопрос о сходимости ряда
остается открытым;
1l =
1
n
n
b
∞
=
∑
в) если , то ряд расходится;
1l >
1
n
n
b
∞
=
∑
с) если , то ряд сходится.
l <∞
1
n
n
b
∞
=
∑
1) все утверждения верны;
2) все утверждения
неверны;
3) верно только а);
4) верно только в);
5) верно только с).
4.
Написать формулу общего члена ряда
12 3 4
5 8 11 14
++ + +… .
1)
5
n
n
+
; 2)
51
n
n
+
;
3)
31
n
n
+
; 4)
61
n
n
−
;
53
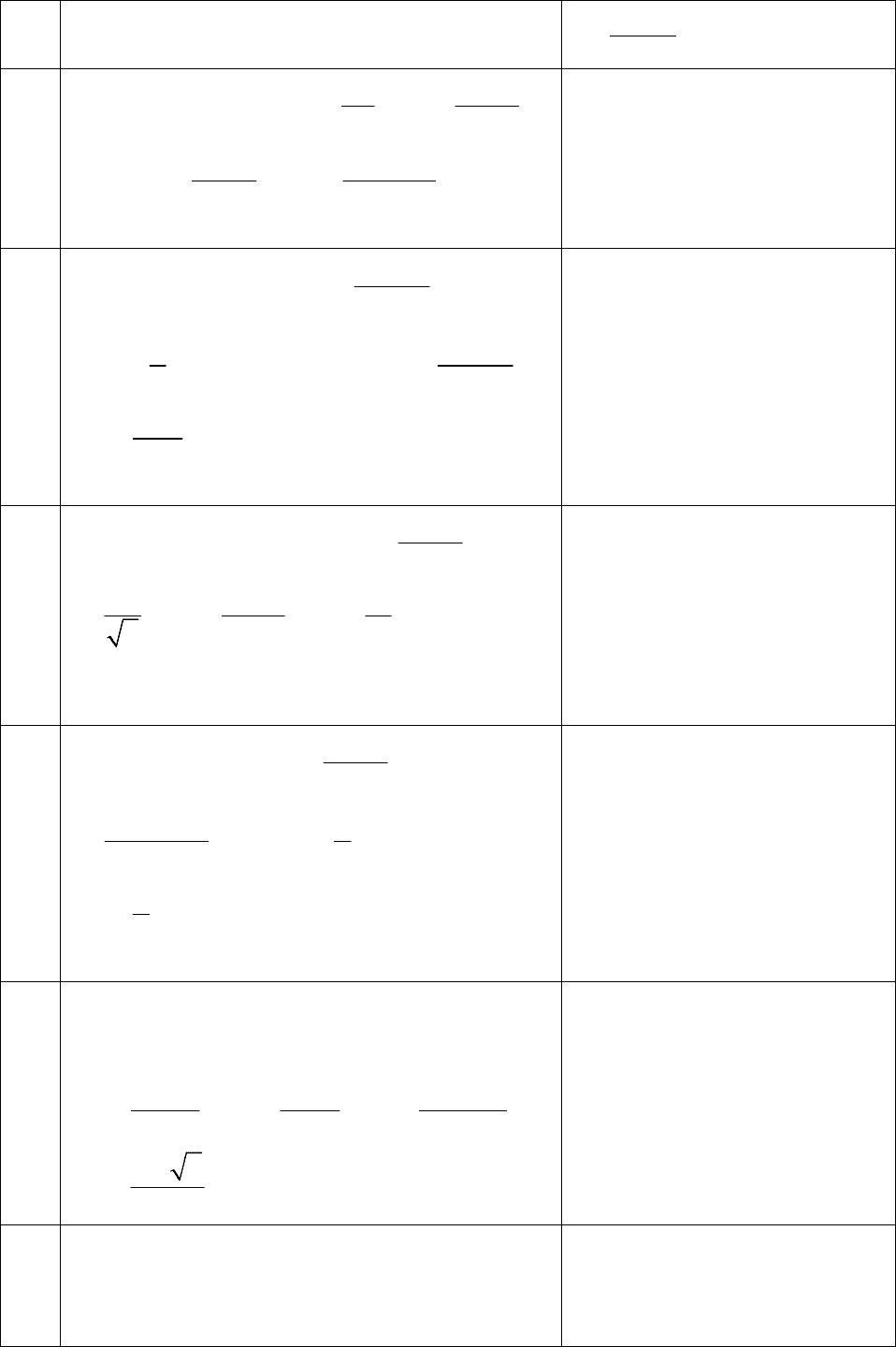
5)
32
n
n
+
.
5
Какие из рядов 1)
1
sin
2
n
n
π
∞
=
∑
; 2)
2
1
!
8
n
n
n
∞
=
+
∑
;
3)
()
3
1
5
1
4
n
n
n
n
∞
=
−
+
∑
; 4)
(
)
1
ln 1
n
n
n
∞
=
+
∑
;
являются знакопостоянными?
1)
1, 2, 4, 5;
2)
1, 2, 4;
3)
2, 4, 5;
4)
2, 4;
5)
Все.
6
Для каких из рядов 1)
3
2
1
3
1
n
n
n
∞
=
2
−
+
∑
; 2)
1
1
1
n
n
n
∞
=
⎛
−
⎜
⎝⎠
∑
⎞
⎟
; 3) ; 4)
1
arctg
n
n
∞
=
∑
2
1
7
53
n
n
n
∞
=
−
∑
;
5)
1
1
n
n
n
∞
=
+
∑
не выполняется необходимое
условие сходимости ряда?
1)
1, 2, 3, 5;
2)
Для всех;
3)
4;
4)
2, 3;
5)
1, 4, 5.
7
Какие из данных рядов 1)
1
53
n
n
n
∞
=
−
∑
; 2)
3
1
2
n
n
∞
=
∑
; 3)
3
1
1
3
n
n
∞
=
+
∑
; 4)
1
1
5
n
n
∞
=
∑
;
5)
1
cos
n
n
π
∞
=
∑
являются сходящимися?
1) Все;
2)
1, 2, 5;
3)
3, 4;
4)
2, 3, 4;
5)
1, 2, 3, 4.
8
Для каких рядов 1)
1
53
n
n
n
∞
=
−
∑
; 2)
(
)
1
ln 1
3
n
n
n
n
∞
=
+
∑
; 3)
1
1
1
n
n
n
∞
=
⎛
+
⎜
⎝⎠
∑
⎞
⎟
; 4) ;
5)
1
arctg
n
n
n
∞
=
∑
1
6
n
n
∞
=
∑
применение признака Коши не
даёт ответа на вопрос о сходимости ряда?
1)
Для всех;
2)
1, 2, 5;
3)
2, 3, 4;
4)
1, 5;
5)
2, 3, 5.
9. С помощью признаков сравнения,
установить какие из перечисленных рядов
сходятся:
а)
2
1
2
12
n
n
n
∞
=
+
∑
; б)
1
1
1
n
n
∞
=
+
∑
; в)
1
1
ln( 1)
n
n
∞
=
+
∑
;
г)
2
1n
nn
nn
∞
=
−
−
∑
1) а); в)
2) все, кроме в)
3) только а)
4) а); г)
5) другой ответ
10. С помощью интегрального признака
установить, какие из перечисленных
рядов сходятся:
1) только а)
2) а); в); г)
3) а); в)
4) б); г)
54

а)
2
1
6
9
n
n
∞
=
+
∑
; б)
2
1
1
4
n
n
∞
=
+
∑
;
в)
2
1
1
61
n
na
∞
=
−+
∑
3
; г)
2
1
1
n
n
n
∞
=
+
∑
5) все
Тема «Знакопеременные ряды»
Если среди его членов есть как положительные, так и отрицательные
действительные числа, то ряд называется знакопеременным. Частный случай
знакопеременного ряда – знакочередующийся ряд а
1
– а
2
+ а
3
+… + (– 1)
n–1
а
n
+… , где все а
i
положительные числа. Любые два его соседних члена имеют
различные знаки.
Знакопеременные ряды исследуются на абсолютную и условную
сходимости.
Знакопеременный ряд называется абсолютно сходящимся, если
сходится ряд
1
n
n
a
+∞
=
∑
, составленный из абсолютных величин членов
знакопеременного ряда. Если же ряд, составленный из абсолютных величин
членов знакопеременного ряда расходится, а сам знакопеременный ряд
сходится, то такой знакопеременный ряд называется условно сходящимся.
Сходимость знакочередующегося ряда исследуется при помощи
признака Лейбница: если члены знакочередующегося ряда убывают а
1
<
а
2
< а
3
…
и
lim 0
n
n
a
→+∞
=
, то знакочередующийся ряд сходится и его сумма не
превосходит первого члена ряда, т.е.
S≤ а
1
.
Пример. Исследовать на сходимость ряд – 1+1/2 –1/3+ …+ (– 1)
n
/ n+ …
Решение. Данный ряд знакочередующийся. Исследуем его на
абсолютную и условную сходимости. Составим ряд, взяв члены ряда по
абсолютной величине, получим гармонический ряд 1+ 1/2+ 1/3+ …+ 1/ n +
…. . Он расходится, поэтому абсолютной сходимости нет. Возможна
условная сходимость, для этого проверим, выполняются ли условия
признака Лейбница. Члены ряда убывают (1 < 1/2 < 1/3 …)
и
(1)
lim lim 0
n
n
nn
a
n
→+∞ →+∞
−
=
=
, следовательно, сам знакочередующийся ряд
сходится.
Ответ: Ряд условно сходящийся.
ОБРАЗЕЦ 30.
Если а
1
, а
2
, …а
n
, … - некоторые действительные
числа, то среди записей:
а) а
1
·а
2
· …·а
n
;
b) а
1
+а
2
+…+а
n
;
все записи;
все, кроме первых
двух;
только запись d);
55
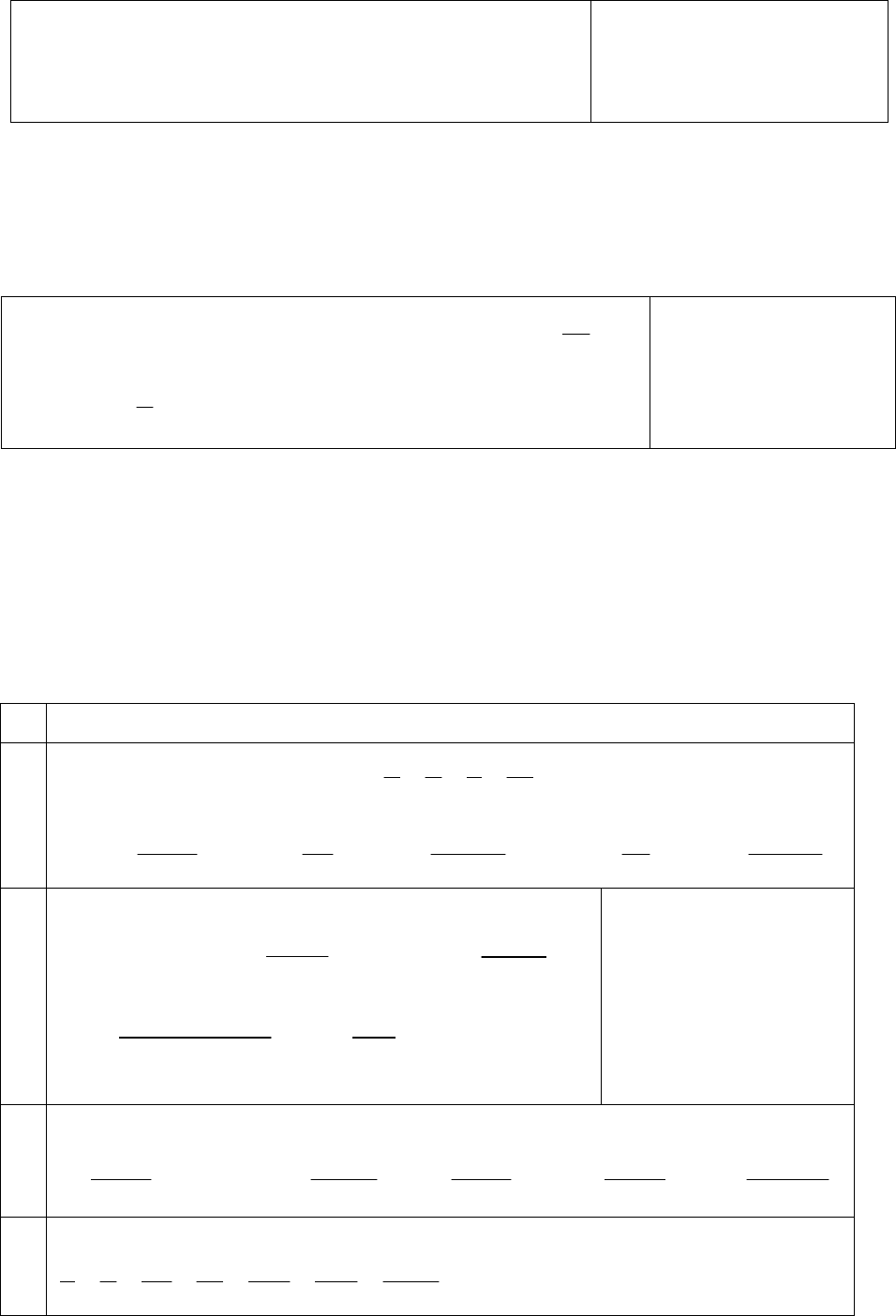
с) а
1
·а
2
· …·а
n
· …;
d) а
1
+а
2
+…+а
n
+ …;
е) –а
1
– а
2
–…–а
n
– …;
числовыми рядами являются:
только запись е);
другой ответ.
Решение. Все записи быть не могут, так как записи а), b), с) не
являются числовыми рядами. Только записи d) и е) удовлетворяют
требованию. Среди возможных ответов такого ответа нет. Поэтому в столбце
ответов следует выбрать последнюю строчку: «другой ответ».
ОБРАЗЕЦ 31.
Среди числовых рядов: а)
1
(1)
n
n
+∞
=
−
∑
; b)
1
1
1
(1)
2
n
n
n
+∞
−
=
−
∑
;
с)
1
1
(1)
n
n
n
+∞
=
−
∑
; d) сходящимися являются….
1
2
n
+∞
=
∑
только а);
только b);
все;
ни один;
только b) и с).
Решение. Глядя на n-ый член каждого ряда и проверяя необходимый
признак сходимости
(
lim 0
n
n
a
→+∞
=
), видим, что для рядов а) и d) он не
выполняется. Ряд с) сходится условно
(см пример выше). Ряд b) –
геометрический с |q |=1/2, что меньше 1, поэтому он сходится . Среди
предложенных рядов только ряды b) и с) – сходящиеся.
Задачи для самостоятельного решения
Формулировка вопроса
1
Формула общего члена ряда
111 1
...
24816
−
+− + имеет вид…
1)
()
1
2
n
n
n
a
−
= ; 2)
1
2
n
a
n
= ; 3)
(
)
1
1
2
n
n
n
a
+
−
=
; 4)
1
2
n
n
a
=
− ; 5)
(
)
1
1
2
n
n
a
n
−
−
=
+
2 Какие из рядов
1)
1
cos
n
n
π
∞
=
∑
; 2)
1
5
!
n
n
n
∞
=
−
∑
3
; 3)
()
1
2
1
1
4
n
n
n
n
∞
−
=
−
+
∑
;
4)
() ( )
4
1
1ln 1
n
n
n
n
∞
=
−+
∑
; 5)
2
1
3
n
n
n
∞
=
−
∑
являются знакочередующимися?
1)
Все;
2)
3, 4, 5;
3)
3, 4;
4)
1, 3, 4, 5;
5)
1, 3, 4.
3 Какой из данных рядов сходится условно?
(
)
2
1
1
n
n
n
∞
=
−
∑
; 2)
()
1
1
6
1
n
n
n
n
∞
+
=
5
+
−
∑
; 3)
(
)
1
1
1
n
n
n
∞
=
−
+
∑
; 4)
(
)
4
1
1
1
n
n
n
∞
=
−
+
∑
; 5)
(
)
1
1!
2
n
n
n
n
∞
=
−
∑
4 Сколько слагаемых необходимо взять, чтобы найти сумму ряда
12 3 4 5 6 7
...
3 9 27 81 243 729 2187
−+−+−+ −
с точностью 0,01?
56
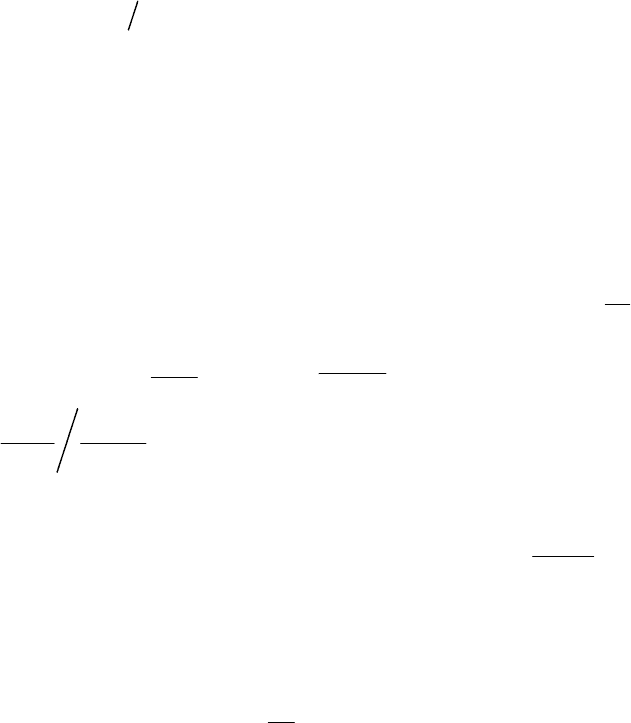
Тема «Сходимость степенных рядов. Применение рядов в
приближенных вычислениях
»
Выражение вида = С
0
n
n
n
Cx
+∞
=
∑
0
+ С
1
х+ С
2
х
2
+ … + С
n
х
n
+ … где С
1
, С
2
,
… , С
n
… – действительные числа (коэффициенты степенного ряда), х –
переменная, а
n
=С
n
х
n
– n-ый (общий) член, называется степенным рядом.
Подставив в степенной ряд конкретное значение переменной, например
х= х
0
, получим числовой ряд. Этот ряд может сходиться, а может и
расходиться.
Множество
D
значений переменной х, при которых ряд сходится,
называется областью сходимости степенного ряда.
Неотрицательное число R, такое, что при |х| < R ряд сходится, а при
|х| > R – расходится, называется радиусом сходимости степенного ряда.
Для степенного ряда радиус сходимости определяется
формулой:
0
n
n
n
Cx
+∞
=
∑
1
lim ( )
nn
n
RCC
+
→+∞
=
.
Из понятия радиуса сходимости ясно, что если известен радиус R,
то
ряд сходится на интервале (–R; R), вне этого интервала – расходится.
Интервал (–R; R) называется интервалом сходимости степенного ряда. На
концах интервала сходимости, т.е. при х = – R и х = R, ряд может как
сходиться, так и расходиться. Поэтому для нахождения области сходимости
надо исследовать сходимость ряда при х = – R и х = R. Результаты
исследования и позволят ответить на поставленный вопрос.
Пример. Найти область сходимости степенного ряда
0
(1)
2
n
n
n
n
x
+∞
=
−
∑
.
Решение. Так как
(1)
2
n
n
n
C
−
=
, то
1
1
1
(1)
2
n
n
n
C
+
+
+
−
=
. Радиус сходимости R будет
равен:
1
1
(1) (1)
lim 2
22
nn
nn
n
R
+
+
→+∞
−−
=
⎛
⎜
⎝⎠
=
⎞
⎟
. Следовательно, интервал сходимости (–2;
2).
Исследуем сходимость ряда на концах интервала. Подставляя в степенной
ряд значение х= –2, получаем числовой ряд
00
(2)
(1) 1
2
n
n
n
nn
+
∞+
==
−
−=
∞
∑
∑
, т. е.
.
Для полученного ряда необходимое условие не выполняется
( ).
То же самое будет, если подставить в степенной ряд
значение х =
2. Получим
1+1+1+1+
lim lim 1 1
n
nn
a
→+∞ →+∞
==
0
2
(1)
2
n
n
n
n
+∞
=
−
∑
, т.е. ∑ (–1)
n
– ряд расходится.
Проведенное исследование показало: найденный интервал сходимости
одновременно будет и областью сходимости степенного ряда.
57
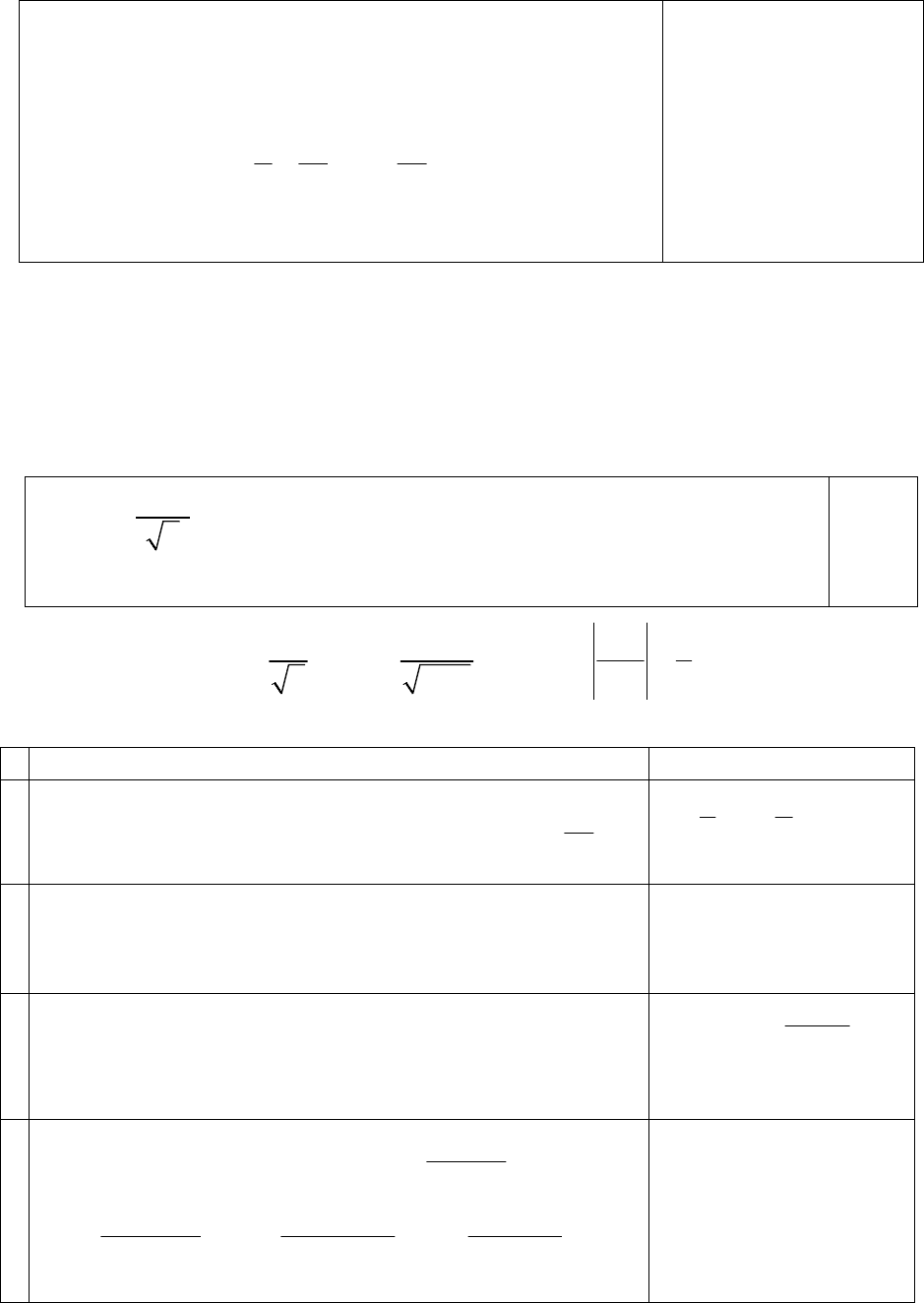
ОБРАЗЕЦ 32.
Если а
i
– действительные числа, а х – переменная,
то среди выражений:
a) а
1
2
+ а
2
2
+ а
3
3
+… + а
n
n
+… ;
b) – х – х – х –…– х –…;
с)
2
11 1
1 ... ...
n
хх х
++ ++ +
;
d) –а
1
– а
2
– а
3
– … – а
n
–…. .
степенными рядами являются ….
все;
; ни одно;
только с);
другой ответ.
Решение. а) и d) – числовые ряды. Оставшихся два ряда, -
функциональные, но не степенные, так как составлены из функций, не
являющимися целыми положительными степенями переменной
х. Поэтому
правильный ответ: ни одно из предложенных выражений не является
степенным рядом.
ОБРАЗЕЦ 33.
Если
1
5
nn
n
x
n
+∞
=
∑
– степенной ряд, то его радиус сходимости равен…
1) ∞; 2) 5; 3)1; 4) 0,2; 5) 0.
∞;
2;
1;
; 0,2;
Решение.
5
n
n
C
n
= ,
1
1
5
1
n
n
C
n
+
+
=
+
.
1
1
lim
5
n
n
n
C
R
C
→+∞
+
=
=
.
Задачи для самостоятельного решения
№
Задание Варианты ответов
1
Найти длину интервала сходимости ряда
1
3
n
n
n
x
∞
=
∑
.
1)
1
3
; 2)
2
3
; 3) 3;
4) 6; 5) 1.
2
Радиус сходимости степенного ряда
равен 2. Найти интервал сходимости.
1
(6)
n
n
n
ax
∞
=
−
∑
1) (0; 2); 2) (–2; 2);
3) (–1; 1); 4) (4; 8);
5) (2; 6).
3
Вычислить приближенно значение выражения
, ограничиваясь суммой первых двух
членов ряда Маклорена для функции
1000 cos 0,5⋅
cos
x
.
1) 500; 2)
1000
3
π
; 3)
1125; 4) 1000;
5) 875.
4
Какие из рядов 1)
1
cos
n
n
π
∞
=
∑
; 2)
()
3
1
1
n
n
n
x
n
∞
=
−
∑
;
3)
()
4
1
25
n
n
n
x
n
∞
=
−
∑
; 4)
()
1
2
1
5
!
n
n
nx
n
+
∞
=
+
∑
;5)
(
)
3
1
ln 1
n
n
n
n
∞
=
+
∑
являются степенными?
1.
2, 3, 4;
2.
Все;
3.
1, 3, 4;
4.
2, 3;
5.
2, 3, 4, 5.
58

ПРИМЕРНЫЕ ВАРИАНТЫ ТЕСТОВ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
ВАРИАНТ №1
1.
Если
ln
y
zx
x
= , то равно …
y
z
′
1)
ху; 2)
2
x
y
; 3)
2
x
y
; 4)
x
y
; 5)
1
ln
y
x
x
+
2.
Если функция двух переменных
33
12 67zx y xy
=
+− +
(0, 0)
x
y>>
, то
её минимум равен…
min
z
3.
Найти неопределённый интеграл
2sin(3 2 )
x
dx−
∫
.
cos(3 – 2x)+C;
0,5
⋅cos(3 – 2x)+C;
cos(3 – 2
x)+C;
2
⋅cos(3 – 2x)+C;
– 4
⋅cos(3 – 2x)+C.
4.
Вычислить
2
0,5
0
x
x
ed⋅
∫
x
.
5.
Сколько интегралов в следующей группе являются несобственными?
а) ; б) ; в) ; г)
∫
+∞
1
xdx
∫
2
1
ln xdx
∫
2
0
ln xdxx
∫
−
∞−
1
2
x
dx
; д)
∫
+
2
1
1x
dx
.
6.
Решением уравнения
1
=
′
yx
является:
1)
x
y
=
; 2) ; 3)
1=y
2
1
x
y −=
; 4) ; 5) .
x
ey =
xy ln=
7.
Если а
i
– действительные числа, а х – переменная, то среди выражений:
а) а
1
2
+ а
2
2
+ а
3
3
+… + а
n
n
+… ; b) х – х – х –…– х –…;
с)
2
11 1
1 ... ...
n
хх х
++ ++ +
; d) а
1
–а
2
– а
3
– … – а
n
–…. .
степенными рядами являются …
1) все; 2) ни одно; 3) только с); 4) другой ответ.
59
ВАРИАНТ №2
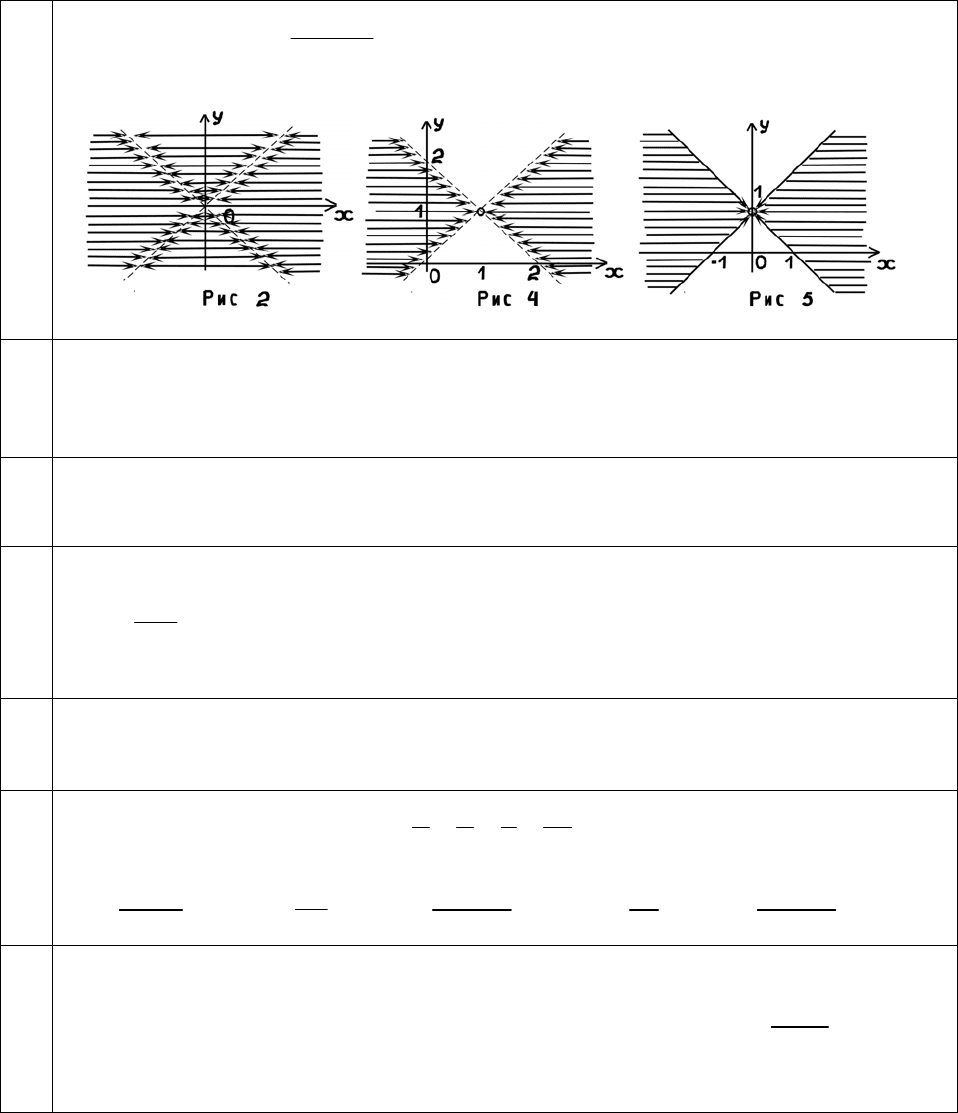
1.
Если функция
2
1
z
yx
=
−
2
, то на плоскости хОу область определения
функции имеет вид…
В ответе запишите номер рисунка.
2.
Найти полный дифференциал функции
2
3
2
Z
xxyy
=
++
в точке
0
(1, 2)M
1) ; 2) ; 3)
878dx dy+ 87dx dy−+ 7dx dy
+
;.4)
12 9dx dy
+
3.
Вычислить
0
5
0,2
50
x
x
edx
−
−
⋅
∫
4. Вычислить несобственный интеграл или установить его расходимость
ln
e
x
dx
x
+∞
∫
1) 1; 2)
е; 3) расходится; 4) е – 1;
5.
Решением уравнения является:
xy
2
tg1 =−
′
1)
x
y cos=
; 2) ; 3)
x
ey =
x
y ctg
=
; 4)
x
y
tg
=
; 5)
Cxy
+
= sin
.
6.
Формула общего члена ряда
111 1
...
24816
−
+− + имеет вид…
()
1
2
n
n
n
a
−
=
; 2)
1
2
n
a
n
= ; 3)
(
)
1
1
2
n
n
n
a
+
−
=
;4)
1
2
n
n
a
=
−
; 5)
(
)
1
1
2
n
n
a
n
−
−
=
+
7.
Зная, что среднее значение m издержек
()
K
x
при изменении объема
производства х от а до b вычисляется по формуле
1
()
b
a
mK
ba
=
−
∫
xdx
,
найти m в случае
2
0, 3, ( ) 8 9abKxxx== =−++
60
