Григорьева Е.В., Дымков М.П. Высшая математика. Второй семестр
Подождите немного. Документ загружается.

Примерный перечень вопросов
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА (Второй семестр)»
1. Определение функции нескольких переменных.
2. Непрерывность функции нескольких переменных.
3. Частные производные и полный дифференциал функции нескольких
переменных.
4. Экстремумы функции нескольких переменных. Необходимые условия.
Достаточное условие экстремума.
5. Понятие об эмпирических формулах. Подбор параметров по способу
наименьших квадратов. Выравнивание по прямой, параболе.
6. Определение первообразной функции и неопределенного интеграла.
Таблица основных интегралов. Основные свойства неопределенного
интеграла.
7. Замена переменной (подстановка) в неопределенном интеграле.
Интегрирование по частям.
8. Интегрирование некоторых выражений, содержащих квадратный
трехчлен.
9. Интегрирование рациональных функций.
10. Геометрическая задача, приводящая к понятию определенного
интеграла. Определение определенного интеграла.
11. Свойства определенных интегралов.
12. Теорема существования первообразной для непрерывной функции.
Формула Ньютона -Лейбница.
13. Замена переменной и интегрирование по частям в определенном
интеграле.
14. Площадь плоской фигуры. Обьем тела вращения.
15. Вычисление объёма произведенной продукции и средней
производительности труда за период.
16. Несобственные интегралы с бесконечными пределами.
17. Несобственные интегралы от неограниченных функций.
18. Дифференциальные уравнения (основные понятия).
19. Дифференциальные уравнения первого порядка с разделяющимися
переменньми.
20. Линейные дифференциальные уравнения первого порядка. Модель
Эванса.
21. Линейные дифференциальные уравнения второго порядка с
постоянными коэффициентами. Метод вариации произвольных постоянных.
22. Понятие числового ряда и суммы ряда. Геометрическая прогрессия.
23. Простейшие свойства сходящихся рядов. Необходимый признак
сходимости ряда.
24. Интегральный признак сходимости.
25. Признак сравнения для положительных рядов.. Признаки Даламбера и
11
Коши.
26. Знакопеременные ряды. Абсолютная и условная сходимость.
27. Знакочередующиеся ряды. Признак Лейбница.
28. Понятие степенного ряда. Область сходимости степенного ряда.
Теорема Абеля.
29. Ряды Тейлора и Маклорена, их применение в приближённых
вычислениях.
30. Дифференцирование и интегрирование степенных рядов.
Основная литература.
1. Яблонский А.И. и др. Под общей ред. С.А.Самаля. Высшая математика.
Общий курс. Мн.: Выш. шк., 2000 г.
2. Кузнецов А.В. и др. Под общей редакцией Яблонского А.И. Высшая
математика. Общий курс. Мн., Выш. шк., 1993 г.
3. Шилкина Е.И. Высшая математика. Ч.1. Мн.: БГЭУ, 2003.
4. Шилкина Е.И., Дымков М.П. Высшая математика Ч.2. Мн.: БГЭУ 2005.
5. Кузнецов А.В., Кузнецова Д.С., Шилкина Е.И. и др. Сборник задач и
упражнений по высшей математике. Общий курс. Учебное пособие. Мн.,
Выш. шк., 1994 г.
6. Общий курс высшей математики для экономистов. Учебник. Под
редакцией проф. В.И. Ермакова. М. Инфра – М. 2006 г.
7. Высшая математика для экономистов /Под ред. Н.Ш. Кремера. – М.:
ЮНИТИ, 2006.
8. Белько И.В., Кузьмич. К.К. Высшая математика для экономистов. Второй
семестр. Экспресс-курс. М.: Новое знание, 2006.
Дополнительная литература.
1. Лихолетов И.И. Высшая математика, теория вероятностей и
математическая статистика. Общий курс. Мн., Выш. шк., 1976 г.
2. Лихолетов И.И., Мацкевич И.П. Руководство к решению задач по высшей
математике, теории вероятностей и математической статистике. Мн.,
Выш. шк., 1969 г.
12

Тематические тестовые задания.
С целью ознакомления студентов с тематикой разработанных тестов
ниже приводится часть тестовых заданий из каждого раздела изучаемой
дисциплины. Эти задания взяты из компьютерной базы данных,
используемой преподавателями кафедры высшей математики БГЭУ для
формирования конкретных тестов, и могут быть использованы студентами
для самостоятельной подготовки. Отметим, что компьютерной системой
предоставляются три типа формы ответов на разрабатываемые тестовые
задания:
1) выбор правильного ответа (или нескольких правильных ответов, если это
оговорено в задании) из набора предложенных вариантов ответа;
2) ввод с клавиатуры правильного ответа (как правило, в виде целого числа,
если не оговорено противное в задании);
3) установление правильного соответствия между элементами множеств.
Приводимые ниже примеры тестовых заданий приводятся или с
полными решениями, или предлагаются варианты ответов:
с подчёркнутым правильным ответом, если предусмотрена форма
ответа №1 (выбор ответа из списка);
правильный ответ, если вопрос второго типа (ввод ответа с
клавиатуры);
вид экрана, содержащего задание и ответ на вопрос третьего типа
(установление соответствия между двумя рядами объектов).
Задания по всему курсу на владение основными
понятиями, терминами и положениями
Одним из пунктов в тестовом задании может быть вопрос общего вида,
выясняющий, как тестируемый ориентируется в основных понятиях,
терминах и определениях программы курса. В задании подобного вида надо
указать соответствие между элементами левой и правой колонок.
ОБРАЗЕЦ 1.
Сопоставьте варианты из правой колонки вариантам из левой:
0
(1)
n
nn
x
+∞
=
−
∑
ФУНКЦИЯ ДВУХ
ПЕРЕМЕННЫХ
z=f(x, y)
СТЕПЕННОЙ РЯД
()
f
xdx
∫
ДИФФЕРЕНЦИАЛЬНОЕ
УРАВНЕНИЕ
xy⋅dx+
2
1
x
−
⋅ln y⋅dy
НЕОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ
13
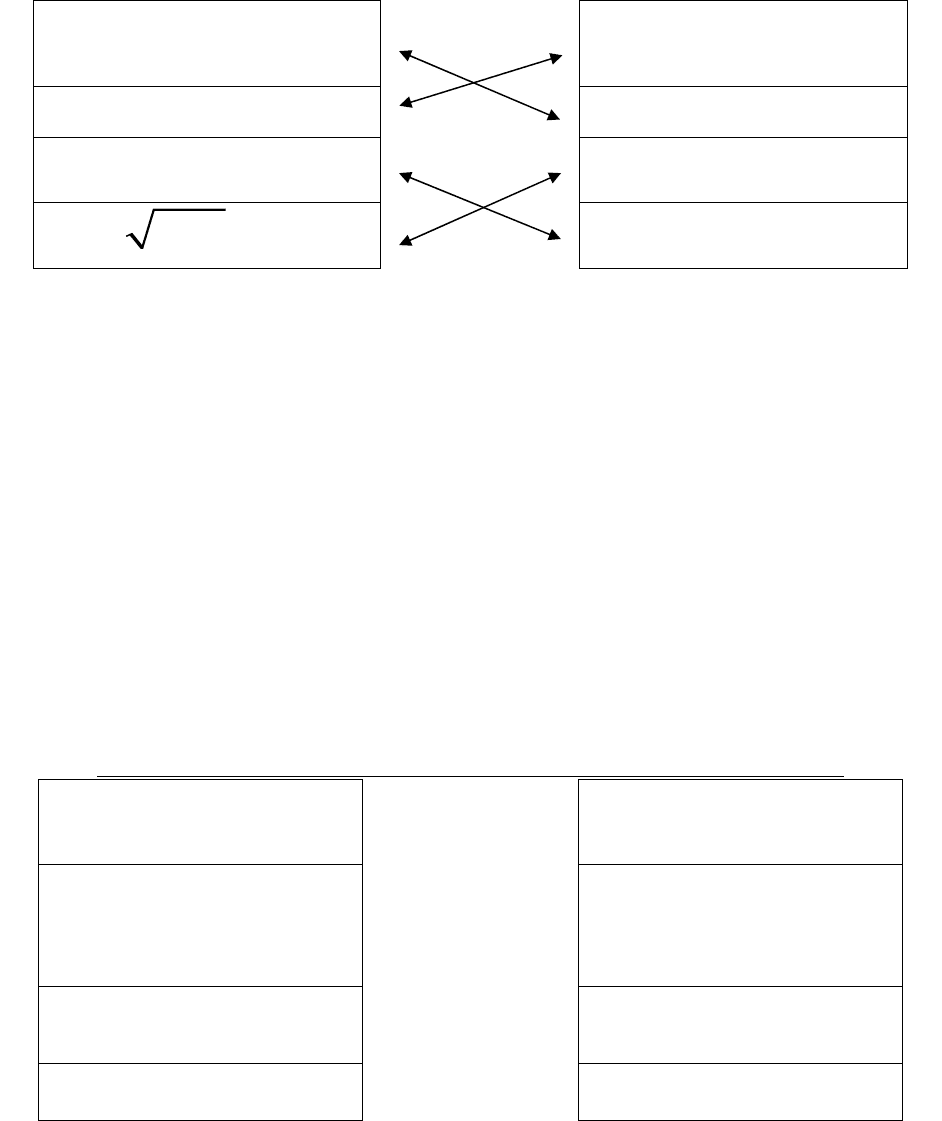
Ответ на вопрос формируется следующим образом. Наводим курсор
мышки на клетку с текстом в правом ряду, нажимаем левую кнопку и, не
отпуская её, переводим курсор на соответствующую клетку в левом ряду,
после чего левую кнопку мышки отпускаем. На экране появится стрелка,
соединяющая эти две клетки. Аналогичную процедуру необходимо
проделать и со всеми оставшимися парами клеток. В итоге ответ на вопрос-
сопоставление будет выглядеть, как это показано на рисунке ниже.
0
(1)
n
nn
x
+∞
=
−
∑
ФУНКЦИЯ ДВУХ
ПЕРЕМЕННЫХ
z=f(x, y)
СТЕПЕННОЙ РЯД
()
f
xdx
∫
ДИФФЕРЕНЦИАЛЬНОЕ
УРАВНЕНИЕ
xy⋅dx+
2
1
x
− ⋅ln y⋅dy=0
НЕОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ
Если возникает необходимость очистить назначенные связи и провести
операцию их назначения заново, необходимо нажать кнопку «очистить»,
расположенную под полем со стрелками.
В тестовом задании может содержаться вопрос, касающийся основных
понятий конкретного раздела. Так, например, для первого раздела “Функции
многих переменных” такими понятиями являются:
функция многих переменных, области определения и изменения;
полное и частное приращения;
частные производные;
полный дифференциал;
экстремум функции.
Например, вопрос по Разделу I может быть вида:
ОБРАЗЕЦ 2.
Сопоставьте варианты из правой колонки вариантам из левой:
z – функция
переменных х и у
– у
2
+1 функция одной
переменной
Если z (см ответ на
редыдущий пункт), то
z (0; у) =
1 – частная
производная по х
x
z
′
=
– 2у dу - частный
дифференциал по у.
y
dz=
z = х – у
2
+1
Ответ на поставленный выше вопрос выглядит следующим образом.
14
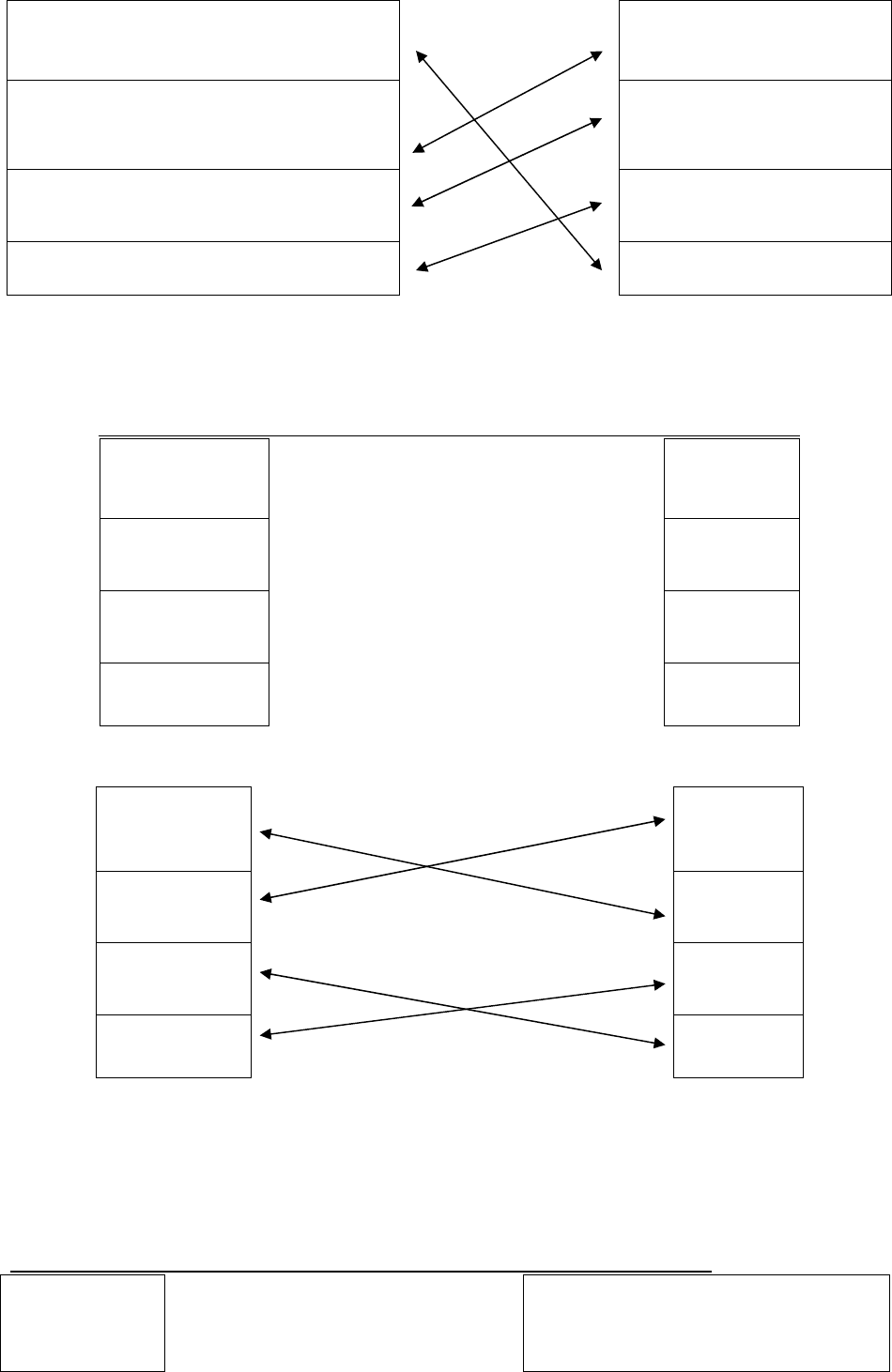
z – функция переменных х и у
– у
2
+1 функция
одной переменной
Если z (см ответ на редыдущий
пункт), то z (0; у) =
1 – частная
производная по х
x
z
′
=
– 2у dу - частный
дифференциал по у.
y
dz=
z = х – у
2
+1
Вопрос по разделу “Неопределённый интеграл ”, требующий сопоставления
элементов левого и правого столбцов, может выглядеть так:
ОБРАЗЕЦ 3.
Сопоставьте варианты из правой колонки вариантам из левой:
()
0dx
′
=
∫
С
0 dx
∫
0
dx
∫
dх
ddx
∫
х + С
Ответ:
()
0dx
′
=
∫
С
0 dx
∫
0
dx
∫
dх
ddx
∫
х + С
Если же вопрос будет выбран из набора вопросов, относящихся к теме
“Определённый интеграл”, то возможен такой вариант:
ОБРАЗЕЦ 4.
Сопоставьте варианты из правой колонки вариантам из левой:
()
d
c
gxdx
∫
ПОДЫНТЕГРАЛЬНАЯ
ФУНКЦИЯ
15
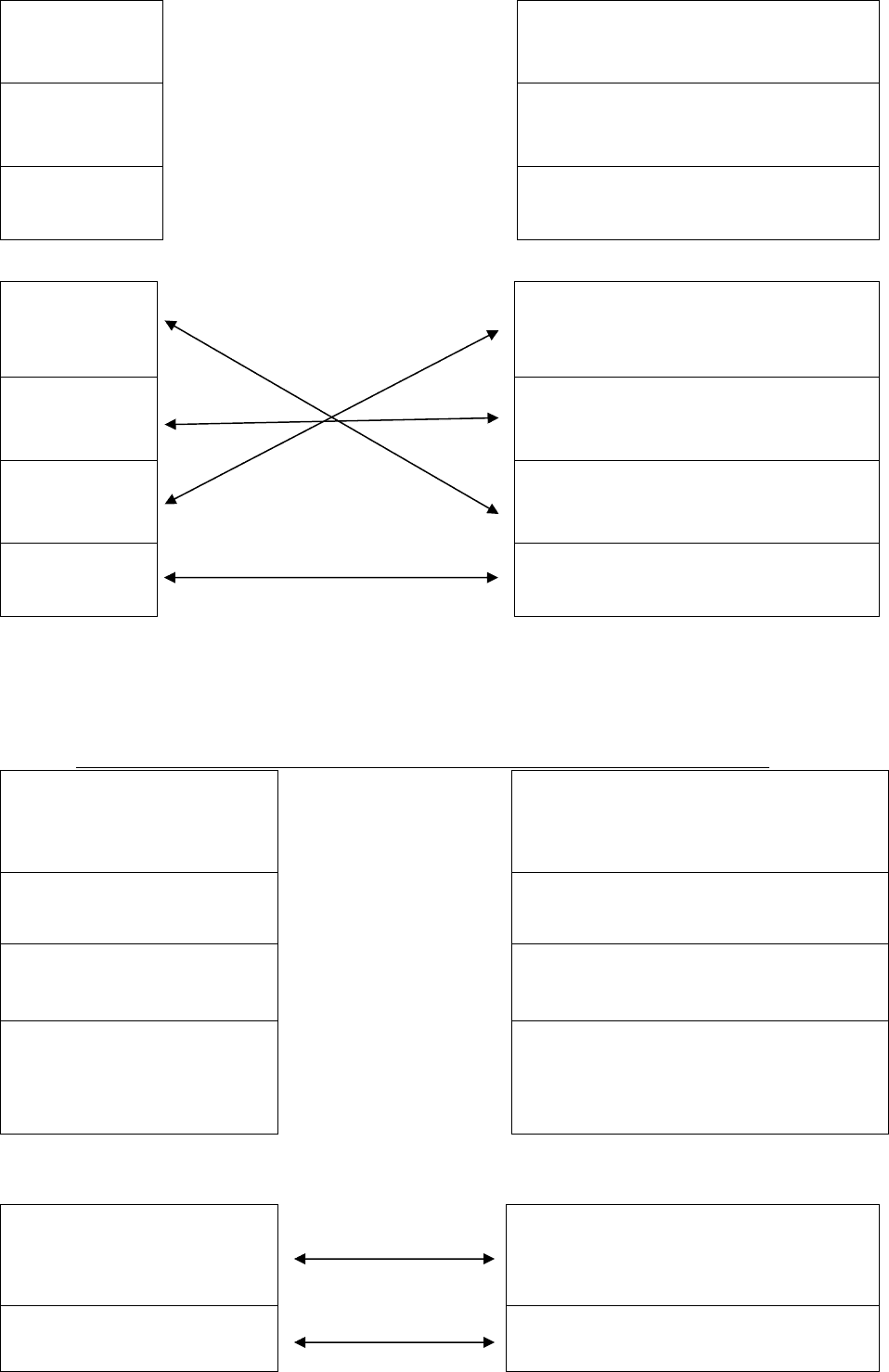
g(x) dx
ПОДЫНТЕГРАЛЬНОЕ
ВЫРАЖЕНИЕ
g(x)
ОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ
[c; d]
ОТРЕЗОК
ИНТЕГРИРОВАНИЯ
Ответ:
()
d
c
gxdx
∫
ПОДЫНТЕГРАЛЬНАЯ
ФУНКЦИЯ
g(x) dx
ПОДЫНТЕГРАЛЬНОЕ
ВЫРАЖЕНИЕ
g(x)
ОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ
[c; d]
ОТРЕЗОК
ИНТЕГРИРОВАНИЯ
Следующий пример – образец возможного вопроса из тематики раздела
“Обыкновенные дифференциальные уравнения”.
ОБРАЗЕЦ 5.
Сопоставьте варианты из правой колонки вариантам из левой:
F(x, y, y′, y″ )=0
обыкновенное
дифференциальное уравнение
второго порядка
y′ +p(x)·y =q(x)
линейное дифференциальное
уравнение первого порядка
y″ – 2y = 0
к
2
– 2 = 0 –
характеристическое уравнение
(y′)
2
– 1 = 0
дифференциальное уравнение
первого порядка второй
степени
Ответ:
F(x, y, y′, y″ )=0
обыкновенное
дифференциальное уравнение
второго порядка
y′ +p(x)·y =q(x)
линейное дифференциальное
16
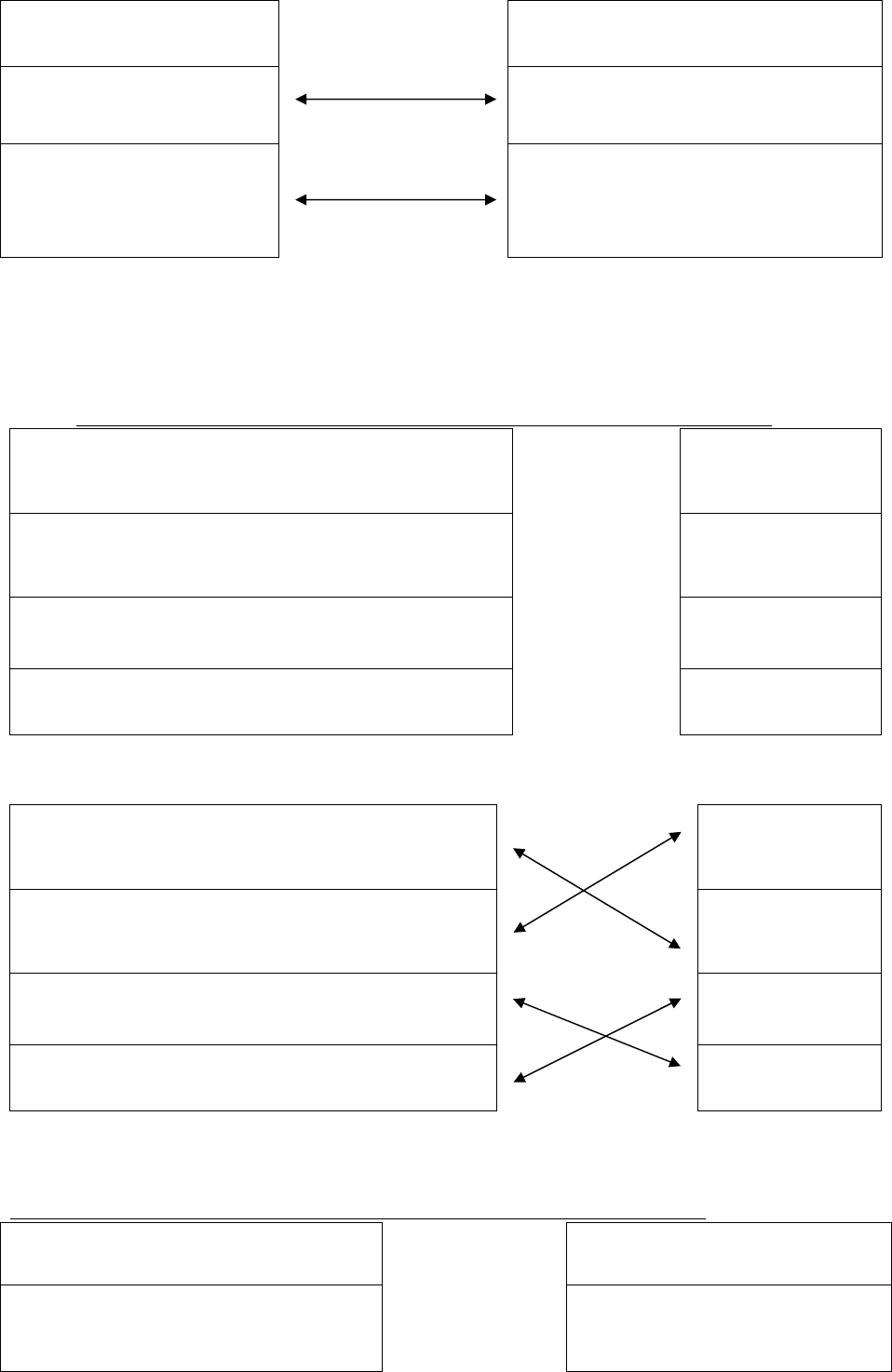
уравнение первого порядка
y″ – 2y = 0
к
2
– 2 = 0 –
характеристическое уравнение
(y′)
2
– 1 = 0
дифференциальное уравнение
первого порядка второй
степени
Следующие два образца – примеры заданий на сопоставление по разделу
“Числовые ряды и степенные ряды”.
ОБРАЗЕЦ 6.
Сопоставьте варианты из правой колонки вариантам из левой:
ЧАСТИЧНУЮ СУММУ ЧИСЛОВОГО
РЯДА ОБОЗНАЧАЮТ
2
n
n-ый ЧЛЕН ЧИСЛОВОГО РЯДА
2+4+8+16+32 + … +
S
n
lim 0
n
n
S
→+∞
=
(СМ. ПЕРВЫЙ ВОПРОС)
ряд
расходится
РЯД И – ТОГДА
n
b
∑
lim 0
n
n
b
→+∞
≠
ряд сходится
Ответ:
ЧАСТИЧНУЮ СУММУ ЧИСЛОВОГО
РЯДА ОБОЗНАЧАЮТ
2
n
n-ый ЧЛЕН ЧИСЛОВОГО РЯДА
2+4+8+16+32 + … +
S
n
lim 0
n
n
S
→+∞
=
(СМ. ПЕРВЫЙ ВОПРОС)
ряд
расходится
РЯД И – ТОГДА
n
b
∑
lim 0
n
n
b
→+∞
≠
ряд сходится
ОБРАЗЕЦ 7.
Сопоставьте варианты из правой колонки вариантам из левой:
С
0
+ С
1
х+ С
2
х
2
+ …+С
n
х
n
.
– ЭТО
СТЕПЕННОЙ РЯД
0
n
n
cx
n
+∞
∑
=
- ЭТО
n-ый ЧЛЕН
СТЕПЕННОГОРЯДА
17
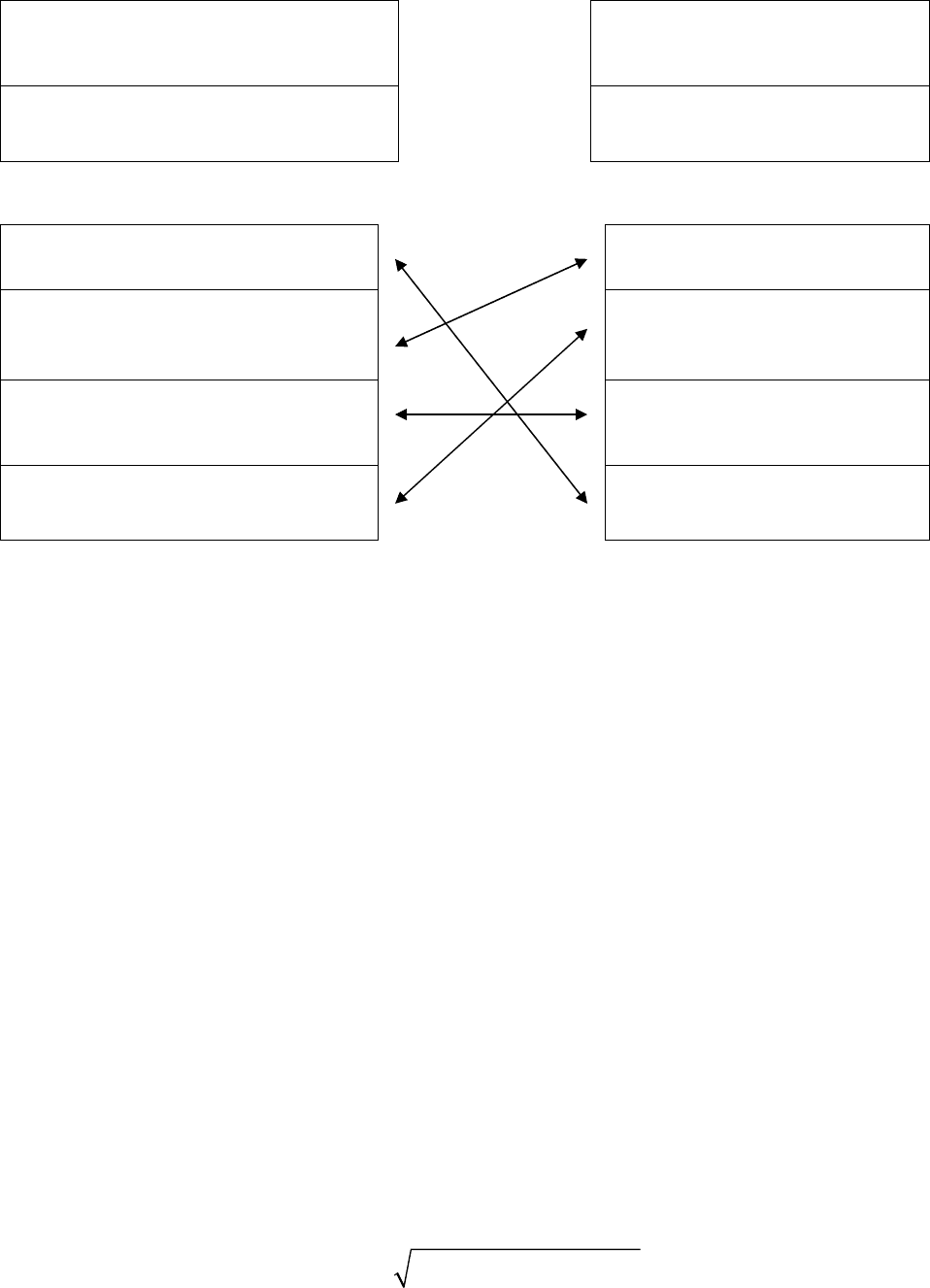
С
n - ЭТО
n-ый КОЭФФИЦИЕНТ
СТЕПЕННОГО РЯДА
С
n
х
n
– ЭТО
ЧАСТИЧНАЯ СУММА
СТЕПЕННОГО РЯДА
Ответ:
С
0
+ С
1
х+ С
2
х
2
+ …+С
n
х
n
.
– ЭТО
СТЕПЕННОЙ РЯД
0
n
n
cx
n
+∞
∑
=
- ЭТО
n-ый ЧЛЕН
СТЕПЕННОГОРЯДА
С
n - ЭТО
n-ый КОЭФФИЦИЕНТ
СТЕПЕННОГО РЯДА
С
n
х
n
– ЭТО
ЧАСТИЧНАЯ СУММА
СТЕПЕННОГО РЯДА
Формы ответов других типов (выбор верного ответа из списка
предложенных или ввод ответа с клавиатуры) уже хорошо знакомы по
первому семестру.
При выполнении теста следует учесть, что последовательность тем
заданий в тесте не совпадает с порядком следования разделов в программе,
так как каждое конкретное тестовое задание формируется системой
случайным образом.
Раздел 1. Функции двух переменных
Тема:
«Функция многих переменных, область определения и область
изменения
»
Пусть D - некоторое множество точек плоскости Oxy. Если каждой
точке M(x, y) из области D соответствует вполне определенное число z ∈ Е ⊂
R, то говорят, что на множестве D задана функция двух переменных x и y.
Переменные x и y называются независимыми переменными, или
аргументами, D - областью определения, или существования, функции, а
множество Е всех значений функции - областью ее значений.
Функциональную зависимость z от x и y записывают в виде z=f(M), z = f(x, y),
z = z(x, y), z = F(x, y) и т.д.
Расстояние между двумя точками A(x
1
, y
1
), B(x
2
, y
2
) на плоскости Oxy
вычисляют по формуле
22
21 21
(,) ( ) ( ).
A
Bxx yy
ρ
=−+−
Функция f(M) имеет пределом число A, , если разность f(M) -
A есть бесконечно малая, когда ρ =ρ(M
MM
0
lim
f(M) = A
→
o,
M) → 0 при любом способе
приближения на плоскости Oxy точки M к точке M
o
18
Функция f(x, y) называется непрерывной в точке M
o
, если .
MM
0
0
lim
f(M) = f(M
→
)
ОБРАЗЕЦ 8.
Сопоставьте варианты из правой колонки вариантам из левой:
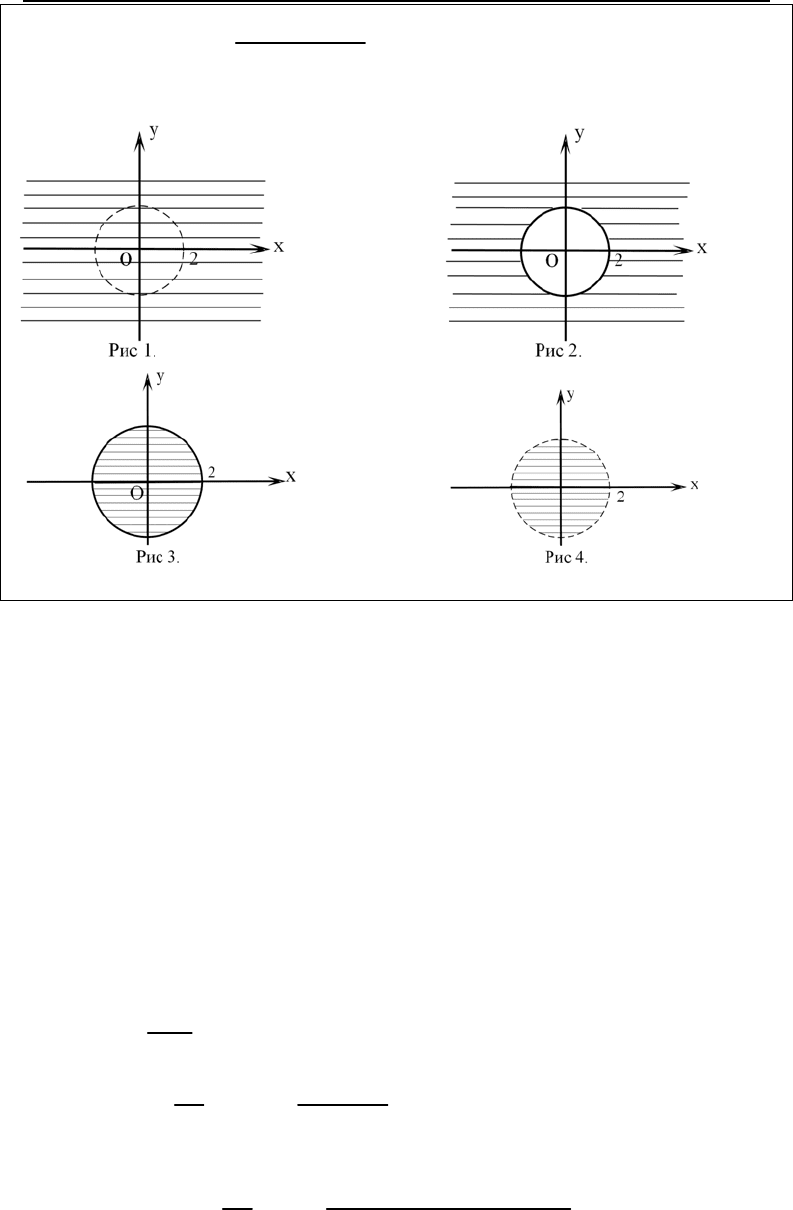
Если функция
2
1
4
z
yx
=
2
−
−
, то на плоскости хОу ее
область определения имеет вид…
В ответе запишите номер рисунка.
Решение. Числитель дроби не должен равняться нулю. Приравняв его к
нулю, получим: у
2
+ х
2
= 4. Это уравнение окружности с центром в начале
координат и радиусом R=2. Поэтому область определения функции – вся
плоскость кроме данной окружности, т.е. ответом является первый рисунок.
Надо в строку ответов ввести число 1.
Тема «Частные производные 1-го и 2-го порядка»
Пусть в некоторой области задана функция z = f(x, y). Возьмем
произвольную точку М(х, у) и зададим приращение Δх переменной х. Тогда
величина Δ
x
z = f( x + Δx, y) – f(x, y) называется частным приращением
функции по х.
Предел
0
lim
x
x
z
x
Δ→
Δ
Δ
называется частной производной
функции z = f(x, y)
по х. Обозначение:
(, )
;; ;(,
xx
zfxy
zf
xx
∂∂
′′
∂∂
).xy
Аналогично определяется частная производная функции по у.
0
(, ) (, )
lim
y
zfxyyfx
yy
Δ→
∂+Δ−
=
∂Δ
y
Если функция f(x, y) определена в некоторой области D, то ее частные
производные
(, )
x
f
xy
′
и (, )
y
f
xy
′
тоже будут определены в той же области
или ее части.
19
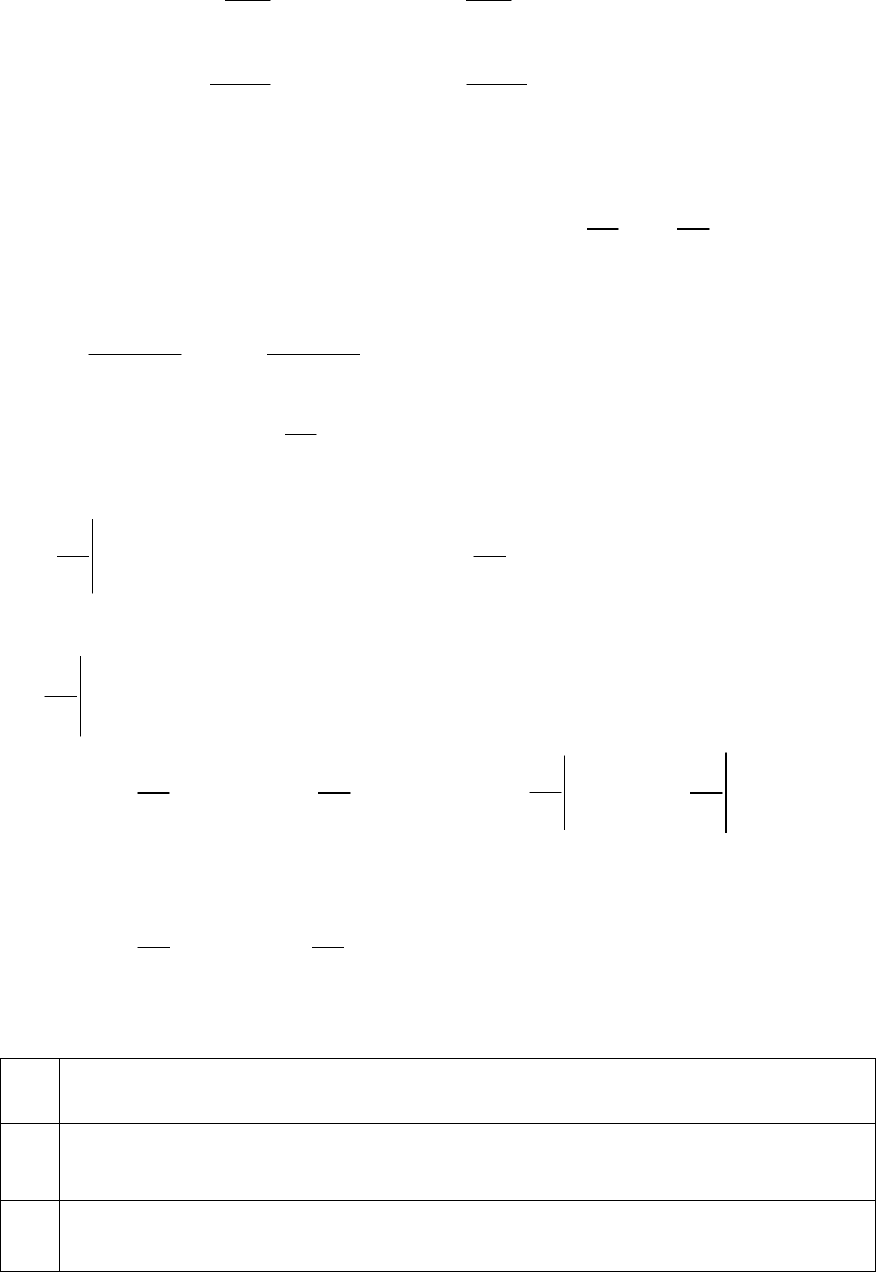
Будем называть эти производные частными производными первого
порядка.
Производные этих функций будут частными производными
второго порядка.
22
22
( , ); ( , );
xx yy
zz
f
x
yf
x
y
xy
∂∂
′′ ′′
==
∂∂
22
(, ); (, );
xy yx
zz
f
x
yf
x
y
xy yx
∂∂
′′ ′′
==
∂∂ ∂∂
Продолжая дифференцировать полученные равенства, получим
частные производные более высоких порядков.
Пример. Вычислить частные производные
z
x
∂
∂
и
z
y
∂
∂
в произвольной
точке
(, )
M
xy
для функции
2
(, ) 3 2
2
f
xy x xy y=− +
и затем найти их
значения
0
(zM)
x
∂
∂
и
0
(zM)
y
∂
∂
, если .
0
(1, 2)M
Решение. Имеем :
z
x
∂
∂
=
22
(32)
x
xxyy
′
−
+=
22
() (3) (2)
xx x
′
=23()023
xxyy
′′
=− +
x
yx x y
′
−
+= −
.
Тогда
0
(1,2)M
z
x
∂
∂
= . Далее:
21 32 4⋅−⋅ =−
z
y
∂
∂
=
22
(32)
y
xxyy
′
−
+=
22
() (3) (2) 03 4
yy y
x
xy y x y
′′′
=− + =−+. Значит,
0
(1,2)M
z
y
∂
∂
= 31 2 4 5
−
⋅+ ⋅ = .
Ответ:
23,
z
x
y
x
∂
=−
∂
34,
z
0
= -4
M
z
x
∂
∂
,
0
= 5
M
z
y
∂
∂
.
x
y
y
∂
=− +
∂
Пример. Найти частные производные функции
z=х
2
–3ху–4у
2
–х+2у+1.
Ответ:
z
х
∂
=
∂
2х–3у–1;
z
у
∂
=
∂
2–3х–8у.
Задачи для самостоятельного решения
№
п/п
Задание
1.
Найти сумму частных производных первого порядка функции
22
Z
xy=+
в точке (–2; 0,5)
2.
Найти произведение частных производных первого порядка
функции
()
Z
arctg x y=+
в точке (0; 0)
20
