Григорьев В.В., Журавлева Н.В. и др. Синтез систем автоматического управления методом модального управления

Подождите немного. Документ загружается.

Учитывая выражение (3.50), система уравнений (3.57) приоб-

ретает вид:

˙e = (A − BK)e − BE˜z

˜z = F

˜z

. (3.58)

Вводя в рассмотрение матрицу описания замкнутой системы

F = A − BK,

модель движения замкнутой системы определяется как

˙e = F e − BE˜z

˜z = F

˜z

. (3.59)

Тогда, вводя обозначение расширенного вектора состояния

модели движения замкнутой системы

¯e =

˜z

модель движения замкнутой системы приобретает вид:

¯e =

F ¯e, (3.60)

где

F =

F −BE

0 F

Из верхнетреугольного блочного вида матрицы описания за-

мкнутой системы, обладающей размерностью (2n − l) × (2n − l),

следует, что характеристический полином замкнутой системы явля-

ется произведением двух характеристических полиномов матрицы

F и матрицы F

, а корни характеристического полинома замкнутой

системы определяются собственными числами матриц F и F

Из проведенного выше анализа следует свойство разделения,

которое заключается в следующем:

— n корней замкнутой системы обеспечивается за счёт выбора

матрицы линейных стационарных связей K;

— оставшиеся (n − l) корней обеспечивается при помощи на-

значения матрицы описания устройства оценки пониженной размер-

ности F

В результате динамический регулятор с устройством оценки

пониженной размерности строится на базе уравнений движения:

ˆz = F

ˆz + Gy + M

u = −Dy − Eˆz

131

Задача синтеза динамического регулятора с устройством

оценки пониженной размерности состоит в выборе матрицы описа-

ния устройства оценки пониженной размерности F

с последующим

вычислением матриц D, E, M

B на основе векторно-матричных

уравнений:

GC = M

A − F

K = DC + EM

3.3.3 Последовательность синтеза динамического регулято-

ра с устройством оценки пониженной размерности

Пусть заданы объект управления (матрицы A,B,C), набор

показателей качества J(t

, σ, ²

, t

, σ

При этом объект управления является объектом управления

с неполной информацией. Этот объект управления обладает свой-

ствами полной управляемости и наблюдаемости и должен функци-

онировать в режиме стабилизации.

Тогда процедура синтеза динамического регулятора с устрой-

ством оценки пониженной размерности состоит из следующих ша-

гов:

1 Синтез матрицы линейных стационарных обратных связей

на основе метода модального управления.

1.1 Из требуемых показателей качества назначается n требу-

емых корней λ

∗

, λ

∗

, . . . , λ

∗

или коэффициентов характеристического

полинома a

∗

, a

∗

, . . . , a

∗

n−1

1.2 Формирование матриц эталонной модели, то есть назна-

чение матрицы Γ по требуемым корням или коэффициентам харак-

теристического полинома и матрицы H из условия полной наблю-

даемости эталонной модели.

1.3 Решение матричного уравнения типа Сильвестра

MΓ − AM = BH

относительно матрицы M с последующим вычислением мат-

рицы линейных стационарных обратных связей K, то есть

K = −HM

−1

1.4 Проверочный расчет, то есть вычисление матрицы опи-

сания замкнутой системы F с последующим нахождение её харак-

теристического полинома или её собственных чисел и сравнение их

с требуемыми коэффициентами или корнями характеристического

полинома.

132

2 Синтез устройства оценки пониженной размерности и вы-

числение матриц, определяющих управляющие воздействия.

2.1 Из требуемых показателей качества назначение (n−l) тре-

буемых корней или коэффициентов характеристического полинома,

то есть нахождение λ

∗

н1

, λ

∗

н2

, . . . , λ

∗

н(n−l)

или a

∗

н0

, a

∗

н1

,. . . , a

∗

н(n− l−1)

2.2 По требуемым корням или коэффициентам характеристи-

ческого полинома формируется матрица описания устройства оцен-

ки пониженной размерности F

2.3 Из условия полной управляемости устройства оценки

пониженной размерности назначается матрица входов устройства

оценки пониженной размерности G.

2.4 Решение матричного уравнения типа Сильвестра вида

GC = M

A − F

относительно матрицы M

2.5 Вычисление произведения M

B и вычисление матриц D

и E из условия выполнения матричного соотношения

D E

= K

−1

В результате выполнения приведённых выше шагов, опреде-

ляется матрица линейных стационарных обратных связей и фор-

мируется устройство оценки пониженной размерности. Структура

алгоритма определения управляющих воздействий представлена на

рисунке 3.16. Как видно из этого рисунка, процедура отыскания

управляющих воздействий состоит из двух этапов. Первый этап

состоит в нахождении матрицы линейных стационарных обратных

связей K. Второй этап заключается в назначении матриц устройства

оценки F

, G и вычислении матриц M

B, D, E.

Пример 3.2 Пусть задан объект управления с неполной информа-

цией, представленный следующей передаточной функцией:

W (s) =

Причём САУ должна функционировать в режиме стаби-

лизации. Исходя из показателей качества, определены требуемые

корни характеристического полинома:

∗

= λ

∗

= −1.

133

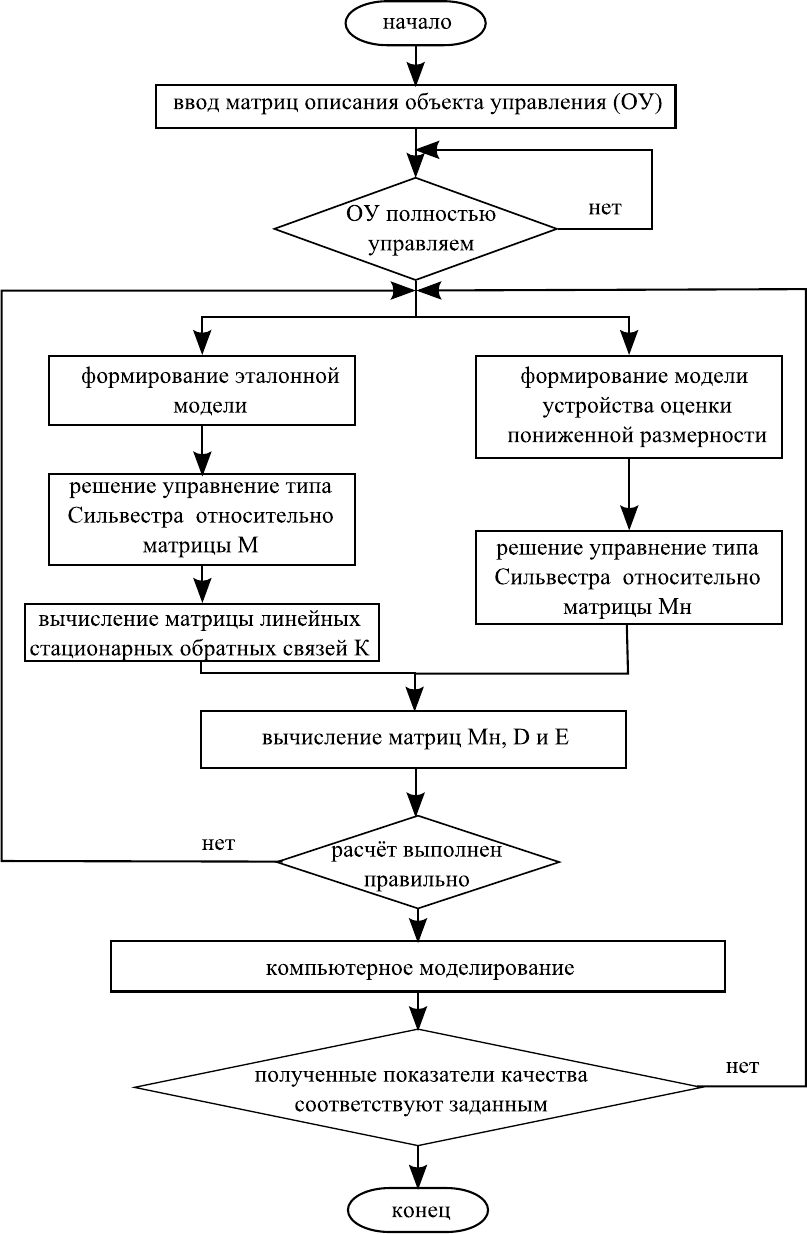
Рисунок 3.16 — Алгоритм определения управляющих воздействий

с устройством оценки пониженной размерности

134

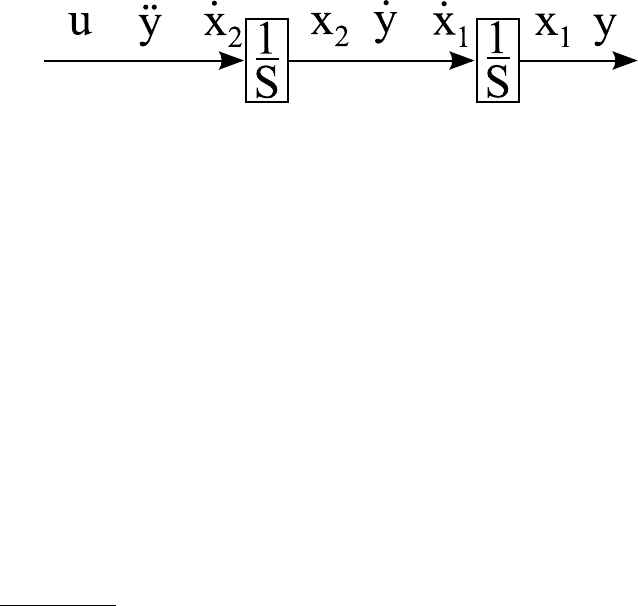
Рисунок 3.17 — Структурная схема объекта управления

Предполагается, что измерению доступна выходная пере-

менная. Объект управления обладает вторым порядком, следова-

тельно, он имеет две составляющие в векторе состояния. Вторая

составляющая вектора состояния не доступна измерению, поэто-

му задан требуемый корень характеристического полинома, пред-

назначенный для синтеза устройства оценки пониженной размер-

ности:

∗

н1

= −10.

Необходимо найти матрицы описания устройства оценки

пониженной размерности F

и матрицы D, E, M

Решение: п На основе передаточной функции составляет-

ся структурная схема объекта управления и вводятся переменные

состояния, которые представлены на рисунке 3.17.

Учитывая введенные обозначения на рисунке 3.17, объект

управления в пространстве состояния описывается следующими

уравнениями:







˙x

= x

˙x

= u

y = x

В векторно-матричном виде объект управления может

быть представлен в виде:











˙x

0 1

0 0

y =

1 0

Тогда матрицы описания объекта управления приобретают

вид:

A =

0 1

0 0

, B =

, C =

1 0

На основе требуемых корней характеристического полино-

135

ма формируется матрица Γ эталонной модели:

Γ =

−1 1

0 −1

, H =

1 0

Матрица линейных стационарных обратных связей нахо-

дится из уравнения типа Сильвестра. Матрица M, имеющая раз-

мерность 2 × 2, формируется следующим образом:

M =

Уравнение типа Сильвестра принимает вид:

−1 1

0 −1

−

0 1

0 0

1 0

Упрощая последнее выражение, получается следующая си-

стема уравнений:











− m

= 0

− m

= 0

−m

= 1

− m

= 0

Решая систему уравнений относительно элементов мат-

рицы M, получается матрица вида:

M =

1 2

−1 −1

Обратная матрица матрицы M находится как

−1

−1 −2

1 1

В результате матрица линейных стационарных обратных

связей вычисляется в виде:

K = −

1 0

−1 −2

1 1

1 2

Осуществляя проверочный расчёт, определяется матрица

замкнутой подсистемы следующим образом:

F =

0 1

0 0

−

1 2

0 1

−1 −2

136

Характеристический полином первой подсистемы замкну-

той системы находится как

D(λ) = λ

+ 2λ + 1 .

Корни характеристического полинома определяются в виде:

= λ

= −1.

Сравнивая полученные корни с требуемыми корнями харак-

теристических полиномов, можно сделать вывод о правильности

нахождения матрицы линейных стационарных обратных связей.

Матрицы эталонной модели, описывающие устройство

оценки пониженной размерности, формируются на основе задан-

ных корней характеристического полинома и условия, что эта мо-

дель обладает свойством полной управляемости. Поэтому матри-

ца F

имеет размерность 1 × 1 и приобретает вид:

= −10,

а матрица G находится из условия полной управляемости устрой-

ства оценки пониженной размерности и имеет вид:

G = 1.

Для формирования устройства оценки пониженной размер-

ности вводится матрица M

. Размерность такой матрицы опре-

деляется порядком объекта управления и порядком устройства

оценки пониженной размерности. Объект управления обладает

вторым порядком, а устройство оценки пониженной размерности

— первым порядком, тогда матрица M

имеет размерность, рав-

ную 1 × 2. В результате матрица M

формируется в виде:

н1

н2

Уравнение типа Сильвестра, которое решается отности-

тельно матрицы M

, имеет вид:

н1

н2

0 1

0 0

− (−10)

н1

н2

1 0

Упрощая последнее выражение, получается следующая си-

стема уравнений:

10m

н1

= 1

н1

+ 10m

н2

= 0

137

В результате решения последнего уравнения матрица M

приобретает вид:

0, 1 −0, 01

Для окончательного формирования динамического регулятора с

устройством оценки пониженной размерности необходимо найти

матрицы: M

B, E, D. Произведение матриц M

и находится сле-

дующим образом:

B =

0, 1 −0, 01

= −0, 01.

Для нахождения остальных двух матриц D и E формиру-

ется составная матрица N в виде:

N =

1 0

0, 1 −0, 01

Обратная матрица матрицы N вычисляется как

−1

1 0

10 −100

Тогда матрицы D и E определяются следующим образом:

D E

1 2

1 0

10 −100

21 −200

Следовательно, динамический регулятор с устройством

оценки пониженной размерности формируется в виде:

ˆz = −10ˆz + y − 0, 01u

u = −21y + 200ˆz

, z(0) = 0.

Структура САУ представлена на рисунке 3.18. На этом рисунке

структура САУ состоит из блоков: блок ОУ, описывающий объ-

ект управления, блок УОПонР, определяющий устройство оцен-

ки пониженной размерности, и блок УУ, задающий управляющее

устройство. Причём блоки УОПонР и УУ объединены в один блок

под названием динамический регулятор.

Для проверки полученного результата осуществляется

компьютерное моделирование. С этой целью составляется схема

моделирования, представленная на рисунке 3.18. В результате та-

кого моделирования были получены графики выходной переменной,

управляющего воздействия и переменной устройства оценки по-

ниженной размерности. Причём начальными условиями объекта

138

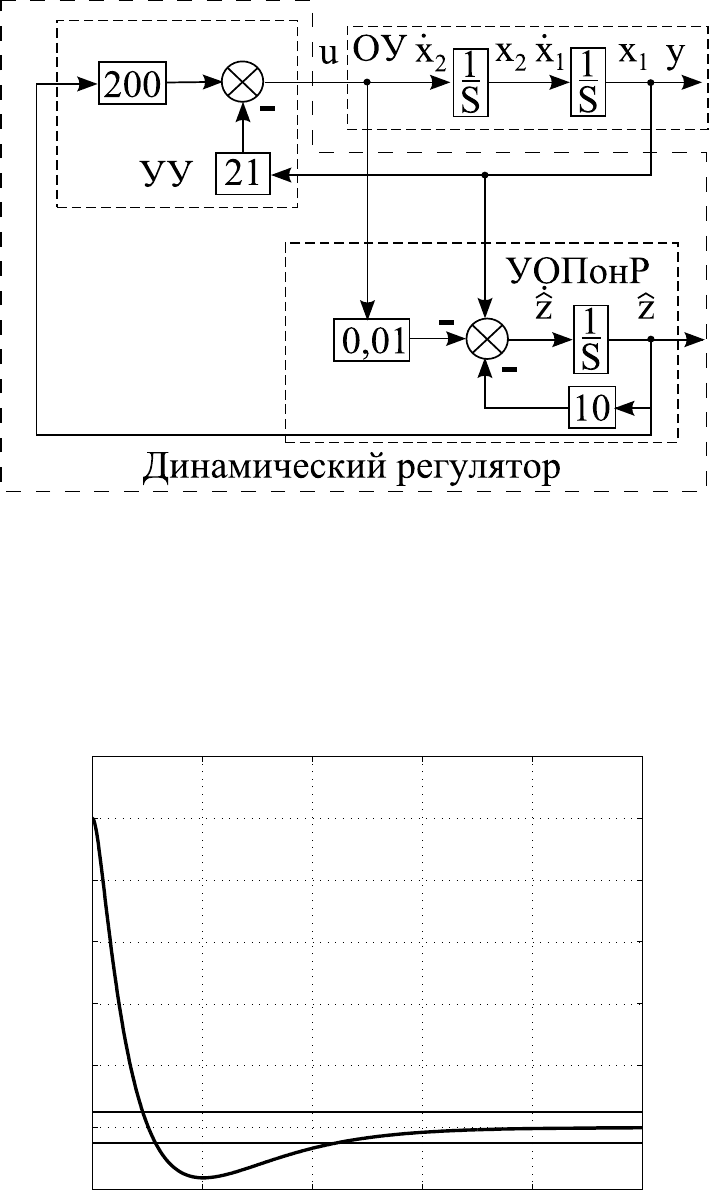
Рисунок 3.18 — Схема моделирования замкнутой системы с дина-

мическим регулятором

0 2 4 6 8 10

−0.2

0.2

0.4

0.6

0.8

1.2

t, c

y(t)

Рисунок 3.19 — График выходной переменной

139

0 2 4 6 8 10

−25

−20

−15

−10

−5

t, c

u(t)

Рисунок 3.20 — График управляющего воздействия

0 2 4 6 8 10

−0.02

0.02

0.04

0.06

0.08

0.1

t, c

z(t)

Рисунок 3.21 — График переменной устройства оценки пониженной

размерности

140