Григорьев В.А., Павлов Ю.М., Аметистов Е.В. Кипение криогенных жидкостей

Подождите немного. Документ загружается.

« кс^

Гг.

Материал

Медь

Никель

Медь

Продолжение табл. 3-2

Теопоотдающая поверхность

Геометрия

Диск

Сфера

Трубка

Размеры

Ориентация

Псверхностные

условия

й =25,4 мм

5 = 21 мм

с?

= 25.4 мм

3 =9,1 мм

й(

= 25,4 мм

й( =51,5X1,9 мм

йг

= 20Х1 мм

й = 1,5 мм

Р = 4950 мм=

Горизонталь-

ная

Горизонталь-

ная

Вертикальная

Горизонталь-

ная

Зеркально-по-

лированная

Гладкая

Шероховатая

Направление измене-

ния теплового потока

Увеличение

Уреличение

Р-10-», Па

Авторы работы

Марто и др.

[123]

Мерте, Кларк

[421]

Паак и др.

[439]

Ружичка

[464]

Вейл, Лаказе

[499]

.-4 соотДтУв^н'о.'""" свойства матер-,алев теплоотдающих поверхностей для групп точек (2, 4), (5, 7), («, Р. ,0. И) приведены в табл. 1-7. 3-6.

для точек 5, 6, 7, 25 — электрический и нестационарное охлаждение; для тоЧки 23 — песта-

ционаряое^Г.ажден;;"."''' '' '' '' ''' обогрева _ электрический; д.

Усгоеия, при которых, получены опытные данные по пузырьковому кипению водорода

Таблица 3-5

Номера

точек по

рис. 3-3

Теплоотдающая псверхнссть

Направление

изменения

теплового

потока

Я-10-», Па

Авторы работы

Номера

точек по

рис. 3-3

Материал

Геометри1

Размены

Ориентация

Поверхностные

условия

Направление

изменения

теплового

потока

Я-10-», Па

Авторы работы

Нержавеющая

сталь Х18Н9Т

Трубка

Г/ = 4Х0,25 ММ

/=294 мм

Вертикальная

—

Увеличение

1,05

(0,79; 0,35;

0,185; 0,073)

И. С. Выходцев

и др. [63]

Монель

Трубка, свер-

нутая Б кольцо

й!^=45 мм —

—

Увеличение

М. п. Малков

и др. [157]

Медь

Торец стержня

(^=5 мм (10 мм)

/=40 мм

Горизонтальная

6—7-й классы

чистоты,

/?2=5-Ь10 МКМ

Увеличение

Данные авторов

Платина

Проволочка,

свернутая в

спираль

с(пр=0,15 мм

/^р=490 мм

Горизонтальная

—

Увеличение

Аструк и др. [211]

—

Трубка, свер-

нутая в кольцо

мм

Горизонтальная

Гладкая

Увеличение

(уменьше-

ние)

1 Вевилогуа и др.

[230]

Медь

Л иск

^•=290 мм^

Горизонтальная

(угол наклона

от 0 до 180°)

2 мкм

Увеличение

(уменьше-

ние)

(1-9,8)

Вевилогуа и др.

[228]

Сплав „Карма"

Полоса

560X^5X0.13 мм

Горизонтальная

(вертикальная,

под угол 45°)

Гладкая (ше-

роховатая)

Увеличение

0,91

Класс и др. [264]

Сплав „Карма"

Полоса

560X^5X0.13 мм

Горизонтальная

(вертикальная,

под угол 45°)

Покрытая

силиконовой

смазкой,

3=13 мкм

Увеличение

0,91

Класс и др. [264]

Продолжение табл.

3-3

Номера

точек

по

рис. 3-3

Теплоотдающая поверхность

Направление

изменения

теплового

потока

р-10-5,

Па

Авторы работы

Номера

точек

по

рис. 3-3

Материал

Геометрия

Размеры

Ориентация

Поверхностные

условия

Направление

изменения

теплового

потока

р-10-5,

Па

Авторы работы

Латунь

Трубка

Й=16 ММ

/=112,8

ММ

Вертикальная

Обработка

16—32

АЗА

Увеличение

0,83

Драйер

и др. [291]

—

Трубка

^=10,4

мм

/==85,7

мм

Горизонтальная

—

Увеличение

Ходж, Бриквед

[240]

Медь

Диск

^=25,4

мм

8=12,7

мм

Горизонтальная

вверх (гори-

зонтальная

вниз, верти-

кальная)

Полировка

Уменьшение

(увеличение)

Коулинг, Мерте

[92]

На

меди

по-

крытие

из не-

ржавеющей

стали

347,

8=0,025

мм

Диск

^=25,4

мм

8=12,7

мм

Горизонтальная

вверх (гори-

зонтальная

вниз, верти-

кальная)

Полировка

Уменьшение

(увеличение)

Коулинг, Мерте

[92]

На

меди

по-

крытие

из теф-

лона,

8=0,038

мм

Диск

^=25,4

мм

8=12,7

мм

Горизонтальная

вверх (гори-

зонтальная

вниз, верти-

кальная)

Уменьшение

(увеличение)

Коулинг, Мерте

[92]

Медь

Плоская

по-

верхность

/=•=500

мм'''

Горизонтальная

—

Увеличение

Рубо

[240]

Напыленные

на

стекло плен-

ки из

меди,

золота, хрома,

германия,

ни-

келя

олоьа

То же

76,2X25,4X1

мм

Гладкая Увеличение

1иерли

[474]

Медь

Трубка

й=1,5 мм

/•=4950

мм«

Горизонтальная

—

Увеличение

Вейл, Лаказе[500]

г=чаои

мм

Примечание.

Для

всех точек, кроме

способ обогрева

—

электрический,

лля

точки

—паровой.

Таблица

3-4

Усговия,

при

которых получены опытные данные

по

пузырьковому кипению гелия

Номера

точек

по

рис. 3-4

Теплоотдаюшал поверхность

Направление

изменения

теплового

потока

/>•10-',

Па

Авторы работы

Номера

точек

по

рис. 3-4

Материал

Геометрия Размеры Ориелтация

Поверхностные

условия

Направление

изменения

теплового

потока

/>•10-',

Па

Авторы работы

Нержавеющая

сталь 12Х18Н9Т

Трубка сг==бхо,з

мм

/=50 мм

Вертикальная

—

Увеличение

1(0,18-1,85)

И. П.

Вишнев

и др. [24]

Бескислородная

медь

Алюминий АВ-000

Трубка

с^=25

мм

/=118 мм

Вертикальная

мкм

Увеличение

(уменьше-

ние)

Л. Б.

Динабург

[51]

Нержавеющая

сталь

Торец

стержня

с(=8 мм

Горизонтальная

/?2=6,5

мкм

/?2=0,7

мкм

Увеличение

(уменьше-

ние)

В. В.

Клименко

[89]

Медь

Торец

стержня

с(=8 мм

Горизонтальная

7?2=6,5

мкм

Увеличение

(уменьше-

ние)

В. В.

Клименко

[89]

Медь

М-1

Бронза ОФ6,5-0,15

Никель

Н-1

Латунь,

Си+ЗОо/о

2п

Нержавеющая

сталь Х18Н9Т

Торец

стержня

й/=10 мм

/=40 мм

Горизонтальная

6—7-й классы

чистоты,

;?2=5ч-10

мкм

Увеличение

Данные

авторов

Медь Диск

Р=490

мм^

Вертикальная

(угол наклона

от 0 до 180°)

мкм

Увеличение

(уменьше-

ние)

(0,06—1,92)

Бевилогуа

и др.

[228]

Электролитическая

медь

Трубка

й=24

мм,

/=54 мм

(й=22

мм,

/=52 мм;

й=32

мм,

/=62 мм)

Вертикальная

400 ^гИ

(полиро-

ванная,

180 и

8Г11;)

Увеличение

(уменьше-

ние)

Бойсин

и др.

[235]

Электролитическая

медь 99,999%

Л иск

й=12,7

мм

е=6,44

мм

Горизонтальная

240 ег!1;

(полированная)

Увеличение

(уменьше-

ние)

Боумен

и др.

[273] !

§5

«а

а>

III

146

оЗ

-е-

о г<1

о«

г ^

^ 2

<0 .

к о;

д а

<и

—

<и

со

€

Щ Д Ор

-со

I-'—

<и со

2 §

(V «У

>. г.

в к

X X

а^ ф

О) г

§ ^

с;

<и а>

>> >,

г ел га

(М о-

о 1>

00 га

та

к то

гае

с:

о а ^

СО 3, ^

к к

к ^

та то та в;

з:

га

л К

га

л К

ч к

га

л К

го

та го с-

Ь: га

СП

ет СП

а.

Е:

а.

о.

2 2

- 2

М 2

ю" О

— ю

II II

со о

II II

хз

ч II

см —•

•ч

С7)

л о

\о

а 2

Юо

со

II о

ь-

с.

1 о э

5 в ® я

к Д д

X К та

о гак

« X Д 2:

з: с-

Г!. 11 с. а.

о ш

та

О)

(_ ш ь со

к та ^

та д со

Ш л Е

Е-,

то

га н _

ко"

н т >;

о. = о.

V а. <и

02 о со

и ш

я г

3 2

СО

о а.

Я 2 =<

<и О)

2 к о

а>

со

то

со

сь

<и

га та

о Е

Ьй —

кг

я к

= я

(О О)

? 3

п в

г I

Е 8

3 о

§ о

I &

1,1°

Ё.

СО

О)

е «

о.

5 Ё

& ^

.е

Уравнения Д. А. Лабунцова (3-15), (3-18) удовлетворительно

гласуются с нашими данными по кипению гелия на поверхности!

меди, а для кипения азота и кислорода теоретические кривые с^

гаются к экспериментальным данным, полученным на поверхности

нержавеющей стали.

Уравнение С. С. Кутателадзе (3-3) располагается приблизител

в середине между данными, полученными нами на поверхностях из м

и нержавеющей стали.

Несмотря на кажущееся преимущество уравнения (3-3) перед с

ношениями (3-15), (3-18), (3-21), было бы неверным отдавать ему п

почтение, поскольку соответствующим изменением постоянных в э

соотнощениях также можно добиться лучшего согласования эксп«

ментальных данных с расчетными. Кроме того, уравнения Д. А. Лае

цова (3-15), (3-18) представляются нам более физически обоснован

ми, нежели уравнение С. С. Кутателадзе (3-3), и поэтому могут служ

основой для дальнейших уточнений (например, введением в них

учтенных факторов). При давлениях, не очень близких к ркр, соотно

ния (3-15), (3-18) и (3-21) практически учитывают влияние давле

на коэффициент теплоотдачи.

Большим тормозом в создании приемлемой теории пузырькового

пения является недостаток информации о физической природе вози

новения паровой фазы в перегретой жидкости и влияния всего комш

са поверхностных условий (в первую очередь шероховатости) напрог

зародыщеобразования. Поиски путей учета поверхностных уело

являются одной из первоочередных задач в дальнейшей разработке

рии теплообмена при пузырьковом кипении. В настоящее время, к со:

лению, отсутствуют удовлетворительные решения этой проблемы. Су

ствующие соотношения либо вообще не учитывают влияние характс

стик .поверхности, либо выведены для каких-либо конкретных усло1

Как мы уже отмечали, некоторые из авторов делают попытки уче

в расчетных соотношениях физико-химические характеристики тепле

дающей поверхности через функцию плотности центров парообразс

ния [например, уравнение Зубера (3-11)] или путем введения в

четную зависимость характерной величины шероховатости (см. ура

ние (1-4)]. Однако для практического использования уравнений т

(3-11) и (1-4) требуется для каждого сочетания жидкость — пове

ность нагрева проведение специального экспериментального исслб

вания для определения константы.

Для расчета интенсивности теплоотдачи при кипении в услов

ослабленных полей силы тяжести можно рекомендовать уравне

Ю. А. Кириченко (3-21), подтвержденное многочисленными опытнь

данными по кипению кислорода в широком диапазоне изменения ве

чины ^('0< 1) и давлений /?== (0,04^10)

•

10^ Па.

Авторам не известны работы, в которых содержались бы попы

учесть в соотношениях для расчета интенсивности теплоотдачи та

факторы, как гистерезис (направление изменения теплового поток

геометрию и ориентацию теплоотдающей поверхности в пространс

Ниже мы приводим некоторые результаты наших теоретических исс

дований, позволяющих с известным приближением учесть в расчетн

соотношениях теплофизические свойства материала поверхности на

ва, толщину нагревательного элемента и влияние металлических пок

тий, имеющих хороший тепловой контакт с подложкой.

144

3-2.

УЧЕТ В РАСЧЕТНЫХ СООТНОШЕНИЯХ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ

МАТЕРИАЛА ТЕПЛООТДАЮЩЕЙ ПОВЕРХНОСТИ

В качестве исходной ;МОдели теплооб1мена нами был выбран подход

Д. А. Лабунцова [105] к описанию интенсивности теплоотдачи при пу-

$ырьковом кипении, позволивший получить соотношение (3-15). При

выводе этого соотношения были использованы внутренние характери-

:тики пузырькового кипения (скорость роста парового пузыря йИ.1йх. и

плотность центров парообразования /г). На наш взгляд, оно является

наиболее физически обоснованным. Согласно этой работе при развитом

пузырьковом кипении в большом объеме жидкость вблизи поверхности

нагрева интенсивно перемешивается вследствие процессов роста и отры-

ва паровых пузырей. Интенсивность такого перемешивания характери-

зуется некоторой средней пульсационной скоростью ш, определяющей

эффективную толщину теплового подслоя, от которой зависит конвек-

тивная составляющая переноса теплоты от стенки ^конв- Другой состав-

ляющей теплопереноса является непосредственное испарение в паровые

пузыри, растущие на поверхности нагрева ^„сп- )

В соответствии с [105] эти составляющие можно записать в сле-

дующем виде:

(3-22)

Х'ДГ -

г—ш:

где

'/„СП

^(3-23)

'/^'/конв + '/исп. (3-24)

(/п. (3-25)

Подставив в уравнение (3-25) полученные ранее выражения для

скорости роста парового пузыря (2-87) и плотности центров парообра-

зования (2-106), получим для пузырькового кипения азота, кислорода,

аргона и других близких к ним по свойствам криогенных жидкостей

(условно отнесенных на.ми к I группе, см. § 1-1) из (3-22) — (3-24) после

ряда несложных преобразований соотношение для расчета интенсивно-

сти теплоотдачи, содержащее теплофизические свойства материалк по-

верхности нагрева:

где

С/р" (3-26)

= —т + +

Комплекс Л(Л 1-(-2т) в уравнении (3-26) является сложной функ-

цией теплофизических свойств материала теплоотдающей стенки

( )/Х.ср), физических свойств жидкости и температурного напора.

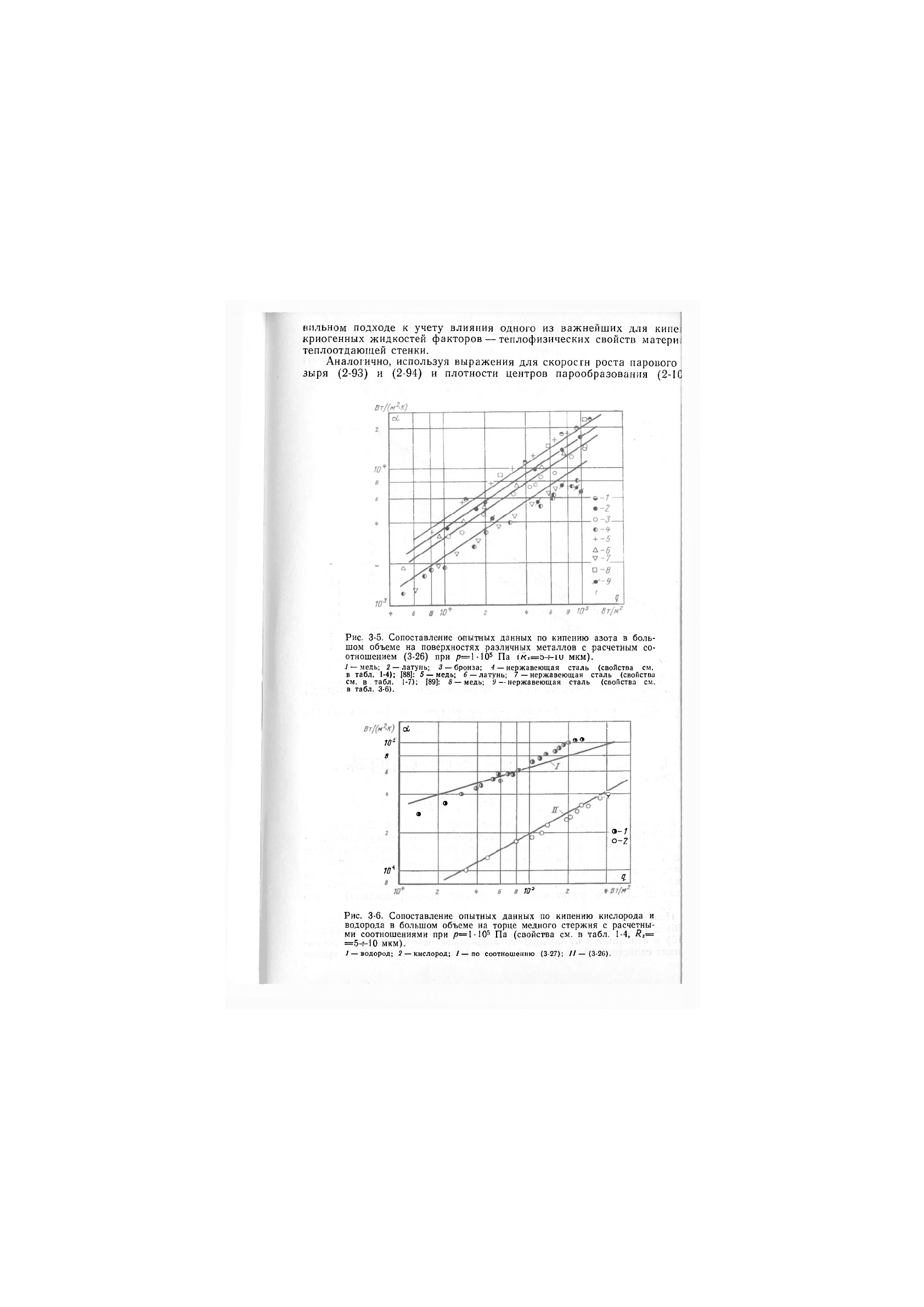
На рис. 3-5 и 3-6 представлено сопоставление опытных данных авто-

ров монографии по кипению азота в большом объеме при атмосферном

давлении на торцах цилиндрических стержней из меди, латуни, бронзы

и нержавеющей стали и кислорода — на торце медного стержня, по-

верхности которых были обработаны по 6—7-му классам чистоты,

а также результаты работ [88, 89] с расчетными, полученными по фор-

муле (3-26). При значениях постоянных С1=0,8-10-'' и С2=10-'' полу-

чено вполне удовлетворительное (±20%) согласование теоретических и

экспериментальных результатов, что говорит о принципиально пра-

148

вильном подходе к учету влияния одного из важнейших для кипе

криогенных жидкостей факторов — теплофизических свойств матери

теплоотдающей стенки.

Аналогично, используя выражения для скоросгн роста парового

зыря (2-93) и (2-94) и плотности центров парообразования (2-1С

Рис. 3-5. Сопоставление опытных данных по кипению азота в боль-

шом объеме на поверхностях различных металлов с расчетным со-

отношением (3-26) при /7=1 •10® Па мкм).

^ — медь; 2 —латунь; 3 — бронза; 4 — нержавеющая сталь (свойства см.

в табл. 1-4); [88]: 5 — медь; 5 —латунь; / — нержавеющая сталь (свойства

см. в табл. 1-7); [89]: в—медь; У — нержавеющая сталь (свойства см.

в табл. 3-6).

10=

10'

Об

,ПФ

-э-7

0-2

-э-7

0-2

10'

Рис. 3-6. Сопоставление опытных данных по кипению кислорода и

водорода в большом объеме на торце медного стержня с расчетны-

ми соотношениями при уО=ЫО^ Па (свойства см. в табл. 1-4, Яг=

=5-^10 мкм).

7 — водород; 2 —кислород; / — по соотношению (3-27); //-(3-26).

част 1_оотношер1ие для расчета интенсивности теплоотдачи при

пузырьковом кипении водорода и неона (II группа) и гелия (III группа):

гр"Д7-„

Сз

Л'ДГ

(3-27)

где теплофизические свойства материала поверхности нагрева входят

в выражение для модуля скорости роста пузыря А (см. § 2-4).

10'

да-

Сб

1 !

с;

1 1

(

1 (

» -7

1 (

(

-5

Ч-6

-7

-5

Ч-6

-7

Су

Г®

-1-

70'

10'

Вт/м'

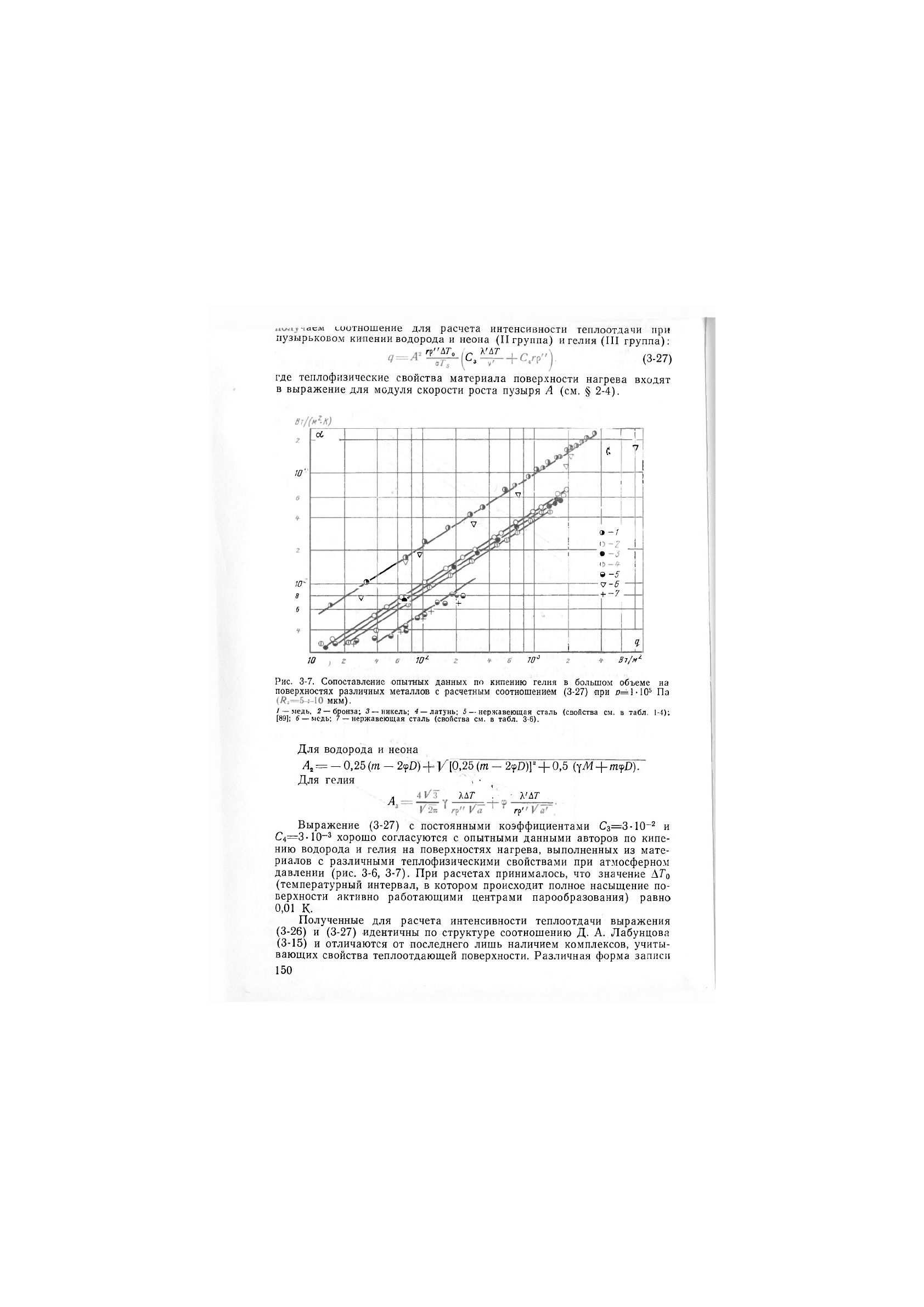
Рис. 3-7. Сопоставление |Опытных данных пп кипению гелия в большом объеме на

поверхностях различных металлов с расчетным соотношением (3-27) при Па

мкм).

/ — медь, 2 —бронза; 3 — никель; 4 —латунь; 5 — нер.жавеющая сталь (свойства см. в табл. 1-4);

[89]; б —медь; 7 — нержавеющая сталь (свойства см. в табл. 3-6).

Для водорода и неона

Л, = - 0,25 (т -

2<^0)

+ )/[0,25(т - 2<р0)]^ + 0,5 (уЖ + туГ»).

Для гелия •• • ^

АДГ • УМ

г?'

Выражение (3-27) с постоянными коэффициентами Сз=3-10-2 и

С4=3-10~^ хорошо согласуются с опытными данными авторов по кипе-

нию водорода и гелия на поверхностях нагрева, выполненных из мате-

риалов с различными теплофизическими свойствами при атмосферном

давлении (рис. 3-6, 3-7). При расчетах принималось, что значение ДГо

(температурный интервал, в котором происходит полное насыщение по-

верхности активно работающими центрами парообразования) равно

0,01 К.

Полученные для расчета интенсивности теплоотдачи выражения

(3-26) и (3-27) идентичны по структуре соотношению Д. А. Лабунцова

(3-15) и отличаются от последнего лишь наличием комплексов, учиты-

вающих свойства теплоотдающей поверхности. Различная форма записп

150

1а

Гз

аэ

а:

в!

о"

э-

сч

С1

э-

о"

Е-,

аз

'С.

•о

€

г-

о"

аз

в;

сс —

СС

.. ь формулах (3-26) и (3-27) связана с некоторыми осо-

бенностями кипения водорода и гелия (см. § 2-5), а также с аппрокси-

мацией функции 1'{В) (см. § 2-4) на различных ее участках, соответ-

ствующих определенным группам криогенных жидкостей. Формулы для

расчета интенсивности теплоотдачи при кипении азота, кислорода, арго-

на, водорода, неона и гелия сведены в табл. 3-5. Там же приведены вы-

ражения для плотности центров парообразования, скорости роста паро-

вых пузырей, которые были использованы при выводе расчетных

соотношений.

В табл. 3-6 приведены теплофизические свойства материалов по-

верхностей нагрева, использованных в опытах автором работы [89].

Таблица 3-6

Теплофизические свойства материаюв поверкноатй нагрева в опытах- работы [89]

т,

Металлы

Вт/(м-К)

а-10',

м'1с

(ВТ-С'/2)/(„2.К:)

80 Медь М-1

2(50

1,46

2,10

Никель Н-2

0,4

0,95

Нержавеющая сталь

9,0

0,068

0,33

Х18Н9Т

4,2

Медь М-1

Нержавеющая сталь

Х18Н9Т

0,35

224

1,0

0,016

0,0033

Примечание. ^ Х'е'рР' = 0,0475-10* (Вт-с)'''2/(м'-К) (для жидкого азота прл 7"^=80 К) ;

КХ'с'рР' = 0,0128-10' (Вт-с'/2)/(м>-К) (для жидкого гелия при К).

Полученные выражения (3-26) и (3-27) справедливы лишь для тех-

нических поверхностей, поскольку при их выводе использовались зави-

симости для плотности центров парообразования (2-106) и (2-107),

справедливые для поверхностей нагрева, обработанных по 6—7-му клас-

сам чистоты. Необходимо отметить, что диапазон давлений, в котором

можно применять полученные формулы, значительно уже, нежели для

исходного соотношения Д. А. Лабунцова (3-15). Последнее обстоятель-

ство связано с введением в соотношение (3-15) комплекса теплофизиче-

ских свойств материала стенки, и хотя для разных по теплофнзическим

свойствам материалов этот диапазон различен, он ограничен давления-

ми, близкими к атмосферному.

Сопоставление зависимостей (3-26) и (3-27) с опытными данными

многочисленных исследований не проводилось из-за отсутствия необхо-

димой информации о шероховатости и теплофизических свойствах мате-

риалов поверхности Экспериментальных образцов, на которых проводи-

лись эксперименты.

Приняв за основу механизм теплоотдачи и структурную формулу для

плотности теплового потока (3-19), использованные Ю. А. Кириченко

[80], аналогичным путем можно получить соотношения для расчета

теплоотдачи с учетом теплофизических свойств поверхности нагрева.

Однако в этом случае имеет место более сильная зависимость интенсив-

ности теплоотдачи от теплофизических свойств материала стенки, чем

это наблюдается на опыте.

152

3-3. УЧЕТ В РАСЧЕТНЫХ СООТНОШЕНИЯХ ТОЛЩИНЫ

НАГРЕВАТЕЛЬНОГО ЭЛЕМЕНТА И МЕТАЛЛИЧЕСКИХ ПОКРЫТИЙ

Определение средней глубины проникновения

температурных возмущений

При анализе экспериментальных данных по теплоотдаче при кии(

НИИ на нагревателях с различной толщиной стенки б отмечалось, чт

влияние ТОЛЩИНЫ проявляется только при значениях, меньших некотс

рого предельного значения 6„ характерного для заданных условий прс

цесса. Таким значением, по-видимому, является глубина проникновени

температурных возмущений (глубина захолаживания — см. § 2-3) дл

идентичных условий кипения на поверхности полуограниченного тел

когда достигается максимальная интенсивность процесса. Очевидно, чт

определение этой величины должно быть первым шагом при анализ

зависимости интенсивности теплоотдачи при кипении от толщины тепле

передающей стенки.

Как известно, возникновение температурных флуктуаций, проникак

щпх в глубь твердого тела, обусловлено испарением микрослоя жидкс

сти в окрестности тех точек поверхности нагрева, где располагаютс

действующие центры парообразования. Для глубины захолаживания

под индивидуальным центром парообразования свойственна та же п(

риодичность, что и для роста паровых пузырей: сначала происходит

увеличение от /г=0 в начальный момент до Лмакс, а затем уменьшени

в обратном направлении. Частота таких флуктуаций в точности соответ

ствует частоте образования пузырей в данном центре парообразовани

[270, 425, 457, 487]. Расположение самих центров достаточно хаотичнс

а суммарная площадь, занимаемая ими, составляет лишь часть обще

площади поверхности нагрева (рассматриваются поверхности нагрев

размеры которых значительно превосходят размеры парового пузыря

Таким образом, оказывается, что для заданных условий кипения (теп

ловая нагрузка, давление, теплофпзические свойства жидкости и мат(

риала поверхности нагрева) глубина захолаживания является фуикцие

3 переменных: времени х. и координат х, у точки поверхности. Есл

мысленно соединить все точки в объеме твердого тела, до которых дока

тывается волна температурного возмущения, то образуется некотора

поверхность захолаживания, которая периодически изменяет свои оче

тания. Поэтому применительно к нашему анализу следует использоват

среднее во времени и по объему значение глубины захолаживания.

Для такого двойного осреднения прежде всего необходимо аналитн

чески описать положение поверхности захолаживания к=\(х, у, т), что

учитывая нестационарность задачи, ее трехмерность и статистически

характер процесса, представляется весьма сложным. Как показано вра

боте [88], задача значительно упрощается, если воспользоваться при

ближенной моделью роста пузыря, рассмотренной в § 2-4 (рис. 2-33)

Напомним основные положения этой модели:

1. Микрослой жидкости под растущим пузырем ограничен с одно

стороны конической поверхностью, а с другой — плоской поверхность»

твердого тела.

2. Рост пузыря на поверхности полуограниченного тела осуществля

ется только путем испарения жидкости с поверхности микрослоя за сче

собственных тепловых ресурсов твердого тела. Как показывают оцеик!

сделанные в работах [68, 106], это положение справедливо для бол1

шинства как обычных, так и криогенных жидкостей при кипении и