Graziani F. (editor) Computational Methods in Transport
Подождите немного. Документ загружается.

68 A. Mezzacappa et al.
[29] Rampp M, Janka HT. Astronomy and Astrophysics 396:361 (2002)
[30] Mezzacappa A, Messer O. Astrophysical Journal submitted (2005)
[31] Burrows A, Thompson T. in Stellar Collapse, ed. C Fryer. Dordrecht: Kluwer
Academic Publishers (2004)
[32] Fuller GM, Mayle R, Wilson JR, Schramm D. Astrophysical Journal 322:795
(1987)
[33] Fuller GM, Mayle R, Meyer BS, Wilson JR. Astrophysical Journal 389:517
(1992)
[34] Qian YZ, Fuller G. Physical Review D 52:656 (1995)
[35] Fuller G, Qian YZ. Physical Review D submitted (2005)
[36] Pantaleone J. Physics Letters B 287:128 (1992)
[37] Pantaleone J. Physics Letters B 342:250 (1995)
[38] Sigl G, Raffelt G. Nuclear Physics B 406:423 (1993)
[39] Mezzacappa A, Bruenn SW. in The Identification of Dark Matter,ed.
N Spooner, V Kudryavtsev. Singapore: World Scientific (1999)

Discrete-Ordinates Methods
for Radiative Transfer
in the Non-Relativistic Stellar Regime
Jim E. Morel
Mail Stop D413, Los Alamos National Laboratory, Los Alamos, New Mexico 87545
jim@lanl.gov
1 Introduction
The purpose of this paper is to briefly describe the application of discrete-
ordinates methods to radiative transfer in the non-relativistic stellar regime.
We consider the non-relativistic regime to be characterized by material ve-
locities less than or equal to one percent of the speed of light. In most appli-
cations, the radiative transfer equations are coupled to the hydrodynamics
equations. We first describe a radiation-hydrodynamics model that consists
of the Euler equations and the radiation transport equation together with
approximations for material-motion effects based upon the assumption of
non-relativistic material velocities. For simplicity, we next focus on a model
of radiative transfer in a static medium that is adequate for the purpose of
describing numerical discretization and solution techniques for the transfer
equation that can also be applied in the more general context of radiation-
hydrodynamics.
2 The Approximate Radiation-Hydrodynamics Model
The hydrodynamics equations and the radiation moment equations can be
expressed to O(v/c) as follows assuming a grey radiation transport approxi-
mation with the transfer equation cast in the Eulerian frame:
• Conservation of fluid mass
:
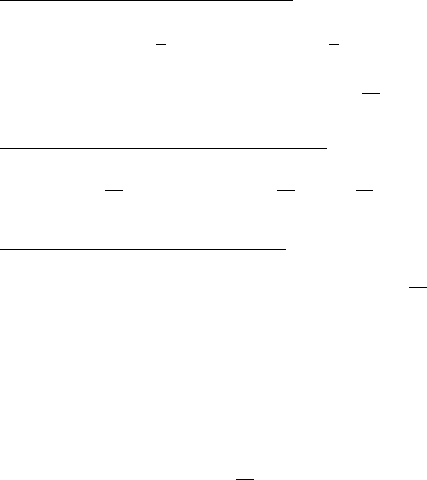
∂
t
ρ + ∂
i
(ρv
i
)=0, (1)
• Conservation of fluid momentum
:
∂
t
(ρv
i
)+∂
j
(ρv
i
v
j
)+∂
i
p =
σ
t
c
F
0,i
−
v
i
c
σ
a
aT
4
− E
0
, (2)
70 J.E. Morel
• Conservation of total fluid energy:
∂
t
1
2
ρv
2
+ ρe
+ ∂
i
1
2
ρv
2
+ ρe + p
v
i
=
−cσ
a
aT
4
− E
0
+
σ
t
c
v
i
F
0,i
, (3)
• Conservation of radiation momentum
:
1
c
2
∂
t
F
i
+ ∂
j
P
ij
= −
σ
t
c
F
0,i
+
v
i
c
σ
a
aT
4
− E
0
, (4)
• Conservation of radiation energy
:
∂
t
E + ∂
i
F
i
= cσ
a
aT
4
− E
0
−
σ
t
c
v
i
F
0,i
, (5)
where ρ is the fluid density, v
i
is component i of the fluid velocity, c is the
speed of light, p is the fluid pressure, e is the specific internal energy of the
fluid, E is the radiation energy density, F
i
is component i of the radiation flux,
P
ij
is element ij of the radiation pressure tensor, E
0
is the comoving-frame
radiation energy density:
E
0
= E −
2
c
2
v
i
(F
i
− v
i
E − v
j
P
ij
) , (6)
F
0,i
is component i of the comoving-frame radiation flux:
F
0,i
= F
i
− v
i
E − v
j
P
ij
, (7)
σ
t
is the macroscopic total cross section, σ
a
is the macroscopic absorption
cross section, and a is the radiation constant. The source terms in (2) through
(5) are expressed in terms of comoving-frame radiation variables. These
comoving-frame variables are defined in terms of Eulerian-frame radiation
variables by (6) and (7). When the comoving-frame variables are eliminated
from (2) through (5) using (6) and (7), certain terms of O(v
2
/c
2
) will ap-
pear. Even though (2) through (5) are only correct to O(v/c), these terms are
not to be neglected because they eliminate spurious equilibrium solutions [1]
and maintain consistency between the Eulerian-frame and comoving-frame
momentum and energy sources. We consider the nonrelativistic limit to be
characterized by v/c ≤ 0.01.
We next describe a very simple approximate model for radiation-hydro-
dynamics with multifrequency radiative transfer in the nonrelativistic limit.
The goal of this approximation is to maintain accuracy in an integral sense
while avoiding the complexities of the equations that are correct to O(v/c).
Since v/c is very small in the nonrelativistic limit, one might be tempted
to neglect material motion corrections to the radiative transfer equation en-
tirely. However, over the course of a calculation, this can result in a signif-
icant loss of energy conservation because the kinetic energy change in the

Discrete-Ordinates Methods for Radiative Transfer 71
fluid due radiation momentum deposition is not removed from the radia-
tion energy field. Thus we use a simple approximation for nonrelativistic
radiation-hydrodynamics that has the following properties:
• Total energy and momentum are conserved.
• Equilibrium solutions are preserved to O(
v
c
).
• The equilibrium diffusion limit is preserved to O(
v
c
).
In the nonrelativistic case, there is little difference between E and E
0
, but the
relative difference between F
0,i
and F
i
can be arbitrarily large. This relative
difference is essentially infinite in the equilibrium state because F
0,i
=0
while F
i
=
4
3
v
i
E to O(v/c). Since the system is locally equilibrated in the
equilibrium diffusion limit, it follows that one can expect a significant relative
difference between F
0,i
and F
i
in this limit. Hence it is generally considered
important to preserve the equilibrium diffusion limit in any approximate
treatment of nonrelativistic radiation-hydrodynamics. See [1] for a formal
asymptotic derivation of the non-relativistic equilibrium diffusion limit.
The first step in the derivation of our approximate model is modify the
hydrodynamics equations and the grey radiation moment equations. Specifi-
cally, we make the following substitutions:
σ
t
c
F
0,i
−
v
i
c
σ
a
aT
4
− E
0
⇒
σ
t
c
F
0,i
, (8a)
cσ
a
aT
4
− E
0
−
σ
t
c
v
i
F
0,i
⇒ cσ
a
aT
4
− E
−
σ
t
c
v
i
F
0,i
, (8b)
F
0,i
= F
i
− v
i
E − v
j
P
ij
⇒ F
i
−
4
3
v
i
E, (8c)
The term neglected in (8a) is a purely relativistic term. Although the radia-
tive transfer equation is always relativistic, the hydrodynamics equations are
purely classical to O(v/c). Furthermore, this term is zero in the equilibrium
diffusion limit. Thus it is reasonable to eliminate this term. In (8b) we replace
E
0
with E in the radiation energy source term. It can be seen from (6) that
this should be a good approximation when v/c ≤ 0.01. Furthermore, E
0
= E
in the equilibrium diffusion limit. Finally, we substitute E/3forP
i,j
in (8c).
This approximation is made simply to avoid calculating the radiation pressure
tensor. This tensor plays a small role in a small term, and the substitution is
exact in the equilibrium diffusion limit. The next step in the derivation is to
replace the modified grey expressions with frequency-dependent expressions
that are equivalent under the grey approximation. In particular,
σ
t
c
F
0,i
⇒
∞
0
4π
σ
t
(ν)
c
I(Ω, ν)
Ω
i
−
4
3
v
i
c
dΩ dν , (9a)
cσ
a
aT
4
− E
⇒
∞
0
4π
σ
a
(ν)
B(ν) − I
−→
Ω
,ν
dΩ dν , (9b)
F
0,i
⇒
∞
0
4π
I
−→
Ω
,ν
Ω
i
−
4
3
v
i
c
dΩ dν , (9c)
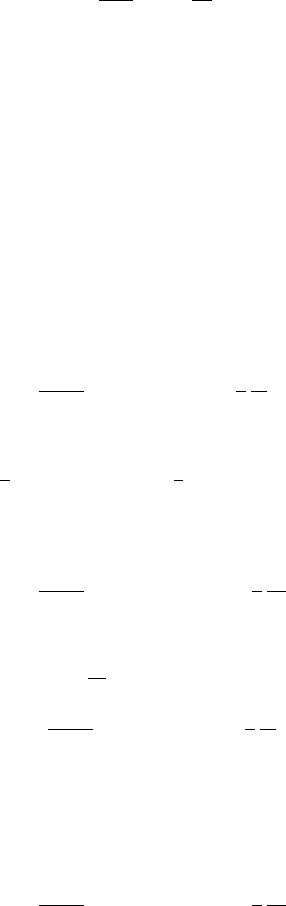
72 J.E. Morel
where
−→
Ω
is the photon direction vector, ν is the photon frequency, I
−→
Ω
,ν
is the angular intensity, B =
2hν
3
c
2
exp
hν
kT
− 1
−1
is the Planck function
and k is the Boltzmann constant. Expression (9b) represents an exact substi-
tution, and (9c) represents a substitution that is exact to O(v/c). However,
(9a) is simply incorrect unless σ
t
is independent of frequency. The transfor-
mations between the Eulerian and co-moving frames being used here are only
correct for angle-energy-integrated quantities [2]. The transformation relat-
ing the co-moving frame flux and the Eulerian frame flux is effectively being
used for frequency-dependent fluxes in (9a).
Accounting for all of these substitutions, our approximate hydrodynamic
equations and multifrequency radiation moment equations can be expressed
as follows:
∂
t
ρ + ∂
i
(ρv
i
)=0 , (10)
∂
t
(ρv
i
)+∂
j
(ρv
i
v
j
)+∂
i
p =
∞
0
4π
σ
t
(ν)
c
I
−→
Ω
,ν
Ω
i
−
4
3
v
i
c
dΩ dν , (11)
∂
t
1
2
ρv
2
+ ρe
+ ∂
i
1
2
ρv
2
+ ρe + p
v
i
=
−
∞
0
4π
σ
a
(ν)
B(ν) − I
−→
Ω
,ν
dΩ dν
+
∞
0
4π
σ
t
(ν)
c
I
−→
Ω
,ν
v
i
Ω
i
−
4
3
v
2
c
dΩ dν , (12)
1
c
2
∂
t
F
i
+ ∂
j
P
ij
=
−
∞
0
4π
σ
t
(ν)
c
I
−→
Ω
,ν
Ω
i
−
4
3
v
i
c
dΩ dν , (13)
∂
t
E + ∂
i
F
i
=
∞
0
4π
σ
a
(ν)
B(ν) − I
−→
Ω
,ν
dΩ dν
−
∞
0
4π
σ
t
(ν)
c
I
−→
Ω
,ν
v
i
Ω
i
−
4
3
v
2
c
dΩ dν . (14)
The radiative transfer equation for static media can be made consistent with
these model equations by adding a P
1
-type correction term to the right side
of the equation:

Discrete-Ordinates Methods for Radiative Transfer 73
1
c
∂I
∂t
+
−→
Ω
·
−→
∇
I + σ
t
I =
1
4π
σ
s
φ + σ
a
B(T )+
1
4π
C
e
+
3
4π
C
f,i
Ω
i
, (15)
where
φ =
4π
I
−→
Ω
,ν
dΩ
, (16)
C
e
= −
4π
σ
t
(ν)
c
I
−→
Ω
,ν
v
i
Ω
i
−
4
3
v
2
c
dΩ
, (17)
C
f,i
=
4π
σ
t
(ν)I
−→
Ω
,ν
4
3
v
i
c
dΩ
. (18)
Note that if we multiply (15) by Ω
i
/c and integrate over all directions and
frequencies, we obtain (13), and if simply we integrate (15) over all direc-
tions and frequencies, we obtain (14). We stress that (15) is an approximate
Eulerian frame transfer equation that is consistent with the other approx-
imations that we have made in the hydrodynamic and radiation moment
equations. The Eulerian frame transfer equation that is correct to O(v/c)
is considerably more complicated than (15) [2]. Our approximate radiation-
hydrodynamics model is completely defined by (10) through (18).
3 Discretization and Solution Techniques
In this section, we discuss discretization and solution techniques for the radia-
tive transfer equation. For simplicity, we consider only the radiative transfer
equation for a static medium and neglect the hydrodynamics equations. In
general, the techniques we discuss here can be applied within a radiation-
hydrodynamics calculation. A discussion of discretization and solution tech-
niques for the full radiation-hydrodynamics equations is beyond the scope of
this paper. The equations we consider consist of a radiative transfer equation:
1
c
∂I
∂t
+
−→
Ω
·
−→
∇
I + σ
t
I =
1
4π
σ
s
φ + σ
a
B(T ) , (19)
and an equation for the material temperature T (r, t):
C
v
∂T
∂t
=
∞
0
σ
a
[ φ − 4πB(T )]dν , (20)
where C
v
is the heat capacity and φ is defined by (16).
Equations (19) and (20) are discretized in direction using the standard S
n
approximation [2,3]. This is basically collocation at a set of discrete directions
that correspond to quadrature points on the unit sphere. The quadrature set

74 J.E. Morel
associated with those discrete directions is also used to perform directional
integrations. For instance, let {
−→
Ω
n
,w
n
}
M
n=1
denote an M-point quadrature
set, then (19) and (20) are directionally discretized as follows:
1
c
∂I
n
∂t
+
−→
Ω
·
−→
∇
I
n
+ σ
t
I
n
=
1
4π
σ
s
φ + σ
a
B(T ) , (21)
C
v
∂T
∂t
=
∞
0
σ
a
[ φ − 4πB(T )]dν , (22)
where
I
n
= I
−→
Ω
n
, (23)
and
φ =
M
n=1
I
n
w
n
. (24)
Equations (19) and (20) are discretized in frequency using the stan-
dard multigroup method [2, 3]. The first step in this method is parti-
tion the frequency domain into G disjoint contiguous intervals or groups:
[ν
1
2
,ν
3
2
),...,[ν
G−
1
2
,ν
G+
1
2
)
where the minimum frequency is ν
1
2
and the
maximum frequency is ν
G+
1
2
.Theg’th group refers to the interval,
[ν
g−
1
2
,ν
g+
1
2
). Next (19) and (20) are discretized as follows:
1
c
∂I
g
∂t
+
−→
Ω
·
−→
∇
I
g
+ σ
t,g
I
g
=
1
4π
σ
s,g
φ
g
+ σ
a,g
B
g
(T ) ,g =1,G, (25)
C
v
∂T
∂t
=
G
g
=1
σ
a,g
[ φ
g
− 4πB
g
(T )] , (26)
where
I
g
=
ν
g+
1
2
ν
g−
1
2
I(ν
) dν
, (27)
B
g
=
ν
g+
1
2
ν
g−
1
2
B(ν
) dν
, (28)
and σ
g
denotes any desired average of σ(ν)overgroupg:
σ
g
= σ(ν)
ν∈[ν
g−
1
2
,ν
g+
1
2
)
. (29)
The physical characteristics of radiative transfer problems place severe
demands upon spatial discretization schemes. In particular, such schemes
must:
Discrete-Ordinates Methods for Radiative Transfer 75
• be at least second-order accurate,
• be highly damped in strongly absorbing media,
• be accurate in optically-thin regions,
• possess the thick diffusion limit,
• behave well with unresolved spatial boundary layers.
In general, lumped discontinuous spatial discretization schemes are required
for radiative transfer. These schemes are usually either finite-element based
[4, 5] or finite-volume based [6]. While lumping of the removal and source
terms is well defined, lumping of the gradient term is also required in multidi-
mensional calculations [7]. There is no general procedure for gradient lumping
and it must generally be performed on a case-by-case basis. Gradient lumping
remains a research topic. The need to possess the thick diffusion limit places
additional demands upon spatial discretization schemes. It is important to
explain exactly what it means for a spatial discretization scheme to possess
the thick diffusion-limit. In this limit, the transport solution is diffusive and
the spatial cells can be arbitrarily thick with respect to a mean-free-path.
The diffusion length is the spatial scalelength for diffusive solutions, and the
diffusion length can be arbitrarily large with respect to a mean-free-path.
Hence, a spatial mesh with cells that are thin with respect to a diffusion
length but arbitrarily thick with respect to a mean-free-path might be intu-
itively expected to yield an accurate solution because the spatial variation of
the exact solution is well resolved by the mesh. Indeed, a scheme that yields
an accurate solution for highly diffusive problems whenever the variation of
the exact diffusive solution is well resolved by the mesh is said to possess the
thick diffusion limit. However, it is important to recognize that convergent
schemes, i.e. schemes with truncation errors that go to zero as the mesh is
refined, do not necessarily possess the thick diffusion limit. A truncation error
analysis yields no information on the behavior of a scheme in this limit. Such
analyses indicate that accurate solutions will be obtained if the mesh cells
are thin with respect to a mean-free-path. Spatial resolution on the order of
a mean-free-path is completely impracical in highly diffusive problems. For
instance, as a problem is made increasingly diffusive, the characteristic width
of the system approaches a fixed value when measured in diffusion lengths
and becomes infinite when measured in mean-free-paths. To determine the
behavior of a spatial discretization scheme in the thick diffusion limit, one
must perform a discrete asymptotic analysis [4, 7–10].
Boundary layers that are a few mean-free-paths thick can exist at the
transitions between non-diffusive and diffusive regions. It can be very difficult
to resolve such layers. In general, an adaptive approach is required because the
locations of these boundary layers usually vary dynamically. Furthermore, in
a multifrequency calculation one may not be able to resolve a boundary layer
on a mean-free-path basis for all frequencies. Thus it is desirable to have
schemes that behave well if not highly accurately with unresolved spatial
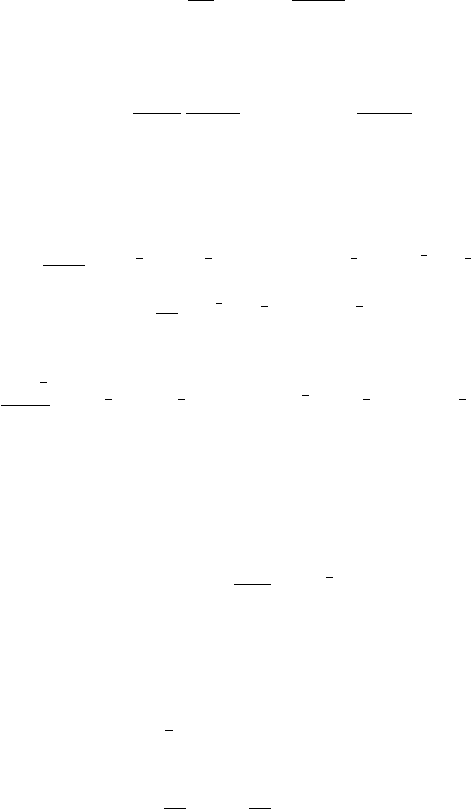
76 J.E. Morel
boundary layers. A discrete asymptotic analysis will reveal this behavior in
addition to the behavior of the scheme on the interior of a diffusive region.
The diffusion limit for radiative transfer is characterized by:
I = B(T ) , (30)
(C
v
+4aT
3
)
∂T
∂t
−
−→
∇
·
4acT
3
3σ
r
−→
∇
T =0 , (31)
where σ
r
is the Rosseland-averaged total cross section:
σ
r
=
∞
0
1
σ
∗
t
(ν)
∂B(ν)
∂T
dν
∞
0
∂B(ν)
∂T
dν
!
−1
. (32)
Equations (19) and (20) are usually solved via a modified Newton’s
method. To illustrate this technique, we first implicitly difference these equa-
tions in time:
1
c∆t
k
I
k+
1
2
− I
k−
1
2
+
−→
Ω
·
−→
∇
I
k+
1
2
+ σ
k+
1
2
t
I
k+
1
2
=
1
4π
σ
k+
1
2
s
φ
k+
1
2
+ σ
a
B
k+
1
2
, (33)
C
k+
1
2
v
∆t
k
T
k+
1
2
− T
k−
1
2
=
∞
0
σ
k+
1
2
a
φ
k+
1
2
− 4πB
k+
1
2
dν . (34)
We let T
∗
denote the latest Newton iterate for the temperature. Then the
linearized equations for the next Newton iteration are obtained by evaluating
the material properties at T
∗
and linearly expanding the Planck function
temperature dependence about T
∗
:
B
n+1
= B
∗
+
∂B
∗
∂T
T
k+
1
2
− T
∗
, (35)
where a superscript “*” denotes a quantity evaluated at T
∗
.Thisisamodi-
fied Newton’s method because the contribution of the material properties to
the Jacobian are neglected. With the expansion given in (35), the material
temperature can be eliminated from the transport equation. Suppressing the
temporal superscript “k +
1
2
”, the linearized temporally-differenced transport
equation can be expressed as:
−→
Ω
·
−→
∇
I + σ
∗
τ
I =
1
4π
σ
∗
s
φ +
1
4π
νχ
∞
0
σ
∗
a
(ν
)φ(ν
) dν
+ ξ, (36)
where:
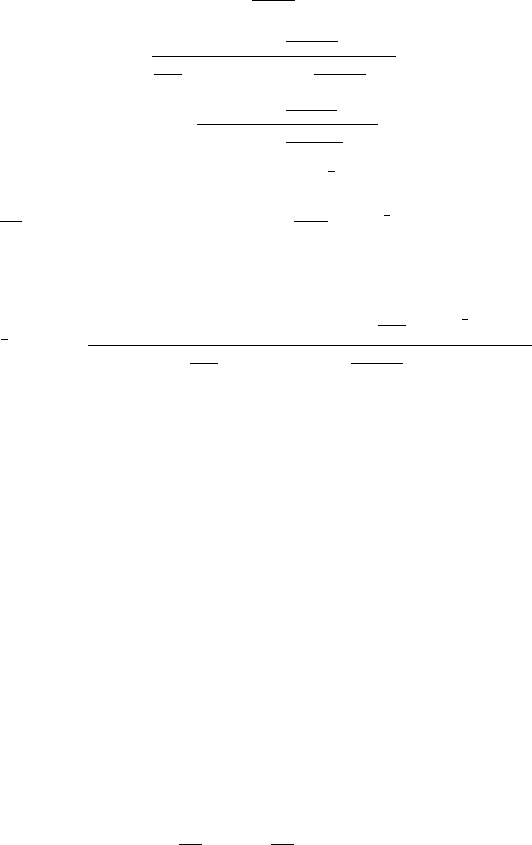
Discrete-Ordinates Methods for Radiative Transfer 77
σ
τ
= σ
t
+ τ, (37a)
τ =
1
c∆t
k
, (37b)
ν =
∞
0
σ
∗
a
(ν)4π
∂B
∗
(ν)
∂T
dν
C
∗
v
∆t
k
+
∞
0
σ
∗
a
(ν)4π
∂B
∗
(ν)
∂T
dν
, (37c)
χ(ν)=
σ
∗
a
(ν)
∂B
∗
(ν)
∂T
∞
0
σ
∗
a
(ν
)
∂B
∗
(ν
)
∂T
dν
, (37d)
ξ = σ
∗
a
B
∗
+ τψ
k−
1
2
−
1
4π
νχ
∞
0
σ
∗
a
(ν
)4πB
∗
(ν
) dν
+
C
∗
v
∆t
k
T
k−
1
2
− T
∗
, (37e)
and the material temperature is given by
T
k+
1
2
= T
∗
+
∞
0
σ
∗
a
(ν)[φ(ν) − 4πB
∗
(ν)] dν +
C
∗
v
∆t
k
T
k−
1
2
− T
∗
C
∗
v
∆t
k
+
∞
0
σ
∗
a
(ν)4π
∂B
∗
(ν)
∂T
dν
. (38)
Equation (38) is used to calculate the temperatures after the linearized trans-
port equation has been solved. We note that (36) has the form of the steady-
state neutron transport equation with σ
a
playing the role of the fission cross
section, ν playing the role of the number of neutrons per fission, χ playing
the role of the fission spectrum, and ξ playing the role of a inhomogeneous
source.
The basic technique for solving (36) is the source iteration technique.
This method is based upon the fact that all coupling between direction and
frequency occurs on the right side of the equation. The operator on the left
side of (36) can be discretized in such a way that a block lower-triangular
coefficient matrix is obtained for each direction and frequency group where
the unknowns in each block are those associated with a single spatial cell.
Such matrices are easily inverted in a direct manner. The inversion process
for each discrete direction and frequency starts where radiation enters the
mesh, proceeds across the mesh, and ends where radiation leaves the mesh.
Hence the inversion process is referred to as a sweep. The iterative process
can be represented in a simplified form as follows:
−→
Ω
·
−→
∇
I
+1
+ σ
∗
τ
I
+1
=
1
4π
σ
∗
s
φ
+
1
4π
νχ
∞
0
σ
∗
a
(ν
)φ
(ν
) dν
+ ξ,(39)
where is the iteration index. The actual iterative process is nested such that
the inner iterations converge the scattering sources for each frequency group
while the absoprtion rate is held fixed, and the outer iterations converge
the absorption rate. The inner source iteration process for group g can be
expressed as
