Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

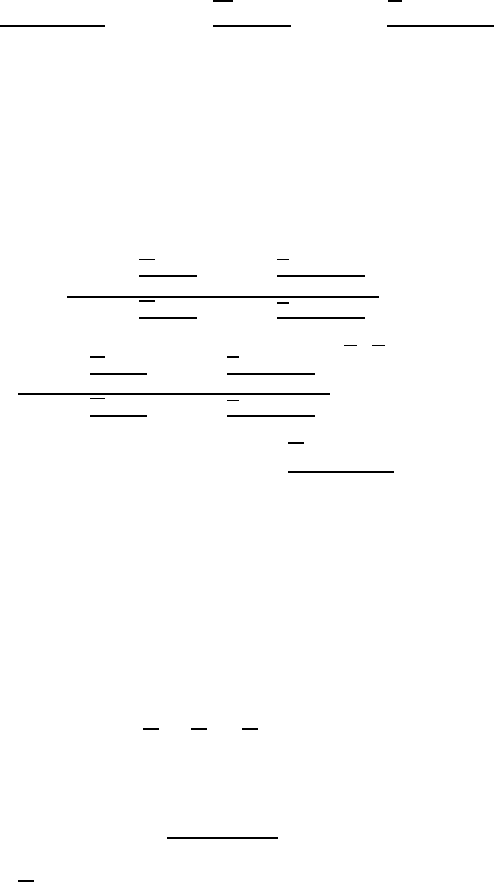
32 1 Thermodynamics of Grain Boundaries

activity and the chemical potentials of real and ideal solutions:

= c

exp



− μ

iideal



= c

exp



− H



· exp



−

− S

iideal



(1.117)

where c

is the molar fraction of the i-th component;

, S

are the partial

characteristics (enthalpy and entropy, respectively) of the real solution; H

the enthalpy of the i-th pure component; S

iideal

is the partial entropy of the

ideal solution.

We obtain the general adsorption isotherm, expressed in terms of the con-

centrations of components at the surface and in the bulk and the thermody-

namic functions of real and ideal solutions in a binary system [26]:

exp



−H



exp



−

−S

1 ideal



exp



−H



exp



−

−S

1 ideal



⎡

⎣

exp



−H



exp



−

−S

2 ideal



exp



−H



exp



−

−S

2 ideal



⎤

⎦

·exp



(γ

− γ

)



(1.118)

The further development of isotherm Eq. (1.118) can be done in terms of

a more speciﬁc, detailed consideration of the thermodynamic functions and

some additional, statistical assumptions, adopted for the sake of simplicity.

We would like to stress that all adsorption isotherms can be derived from

Eq. (1.118), if the corresponding thermodynamic functions are described in

suitable variables.

Then, in the simplest case, the bulk and grain boundary (surface) solutions

are ideal, and the partial areas of the components are equal

A (1.119)

Eq. (1.118) transforms to

1 − c

+ Bc

(1.120)

where B =exp



A (γ

− γ) /(kT)



= b

exp (U

/kT), and U

is the energy

of interaction between the boundary (surface) and the adsorbed atom. The

relationship (Eq. (1.120)) is known as the Zhuchovitskii-McLean isotherm [25].

More complicated is the adsorption for atoms which interact both in the

surface and in the bulk solution. Let us consider this interaction in the Bragg-

Williams approximation — the approximation of a regular solution. For a

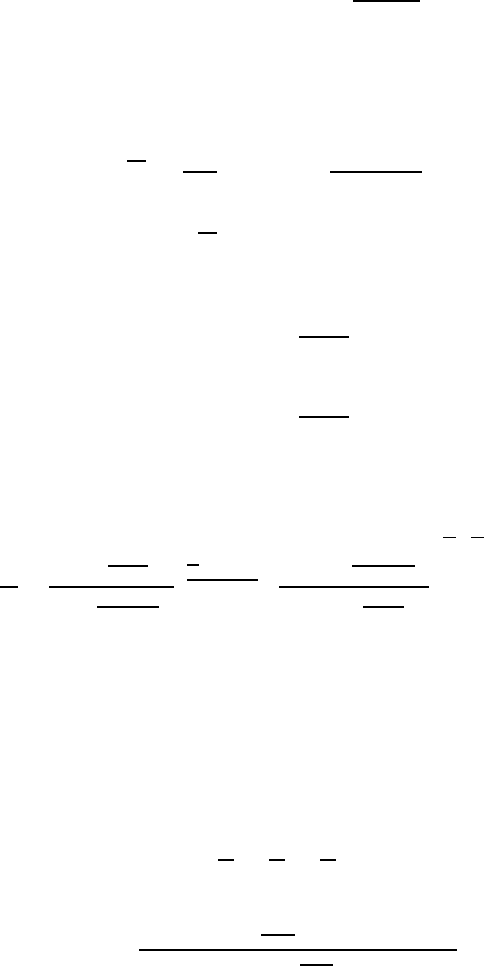
1.2 Thermodynamics of Surfaces 33

regular solution the third factor on the right-hand side of Eq. (1.117) is equal

to one, and all deviations from an ideal solution are determined by the second

factor. The enthalpy H of the regular solution can be expressed as

H = n

+ n

+ ZΔ

+ n

(1.121)

where n

is the number of atoms of the i-th component, Z is the coordination

number, Δ = ε

−(ε

+ ε

)

is the heat of mixing with ε

i−i

, ε

i−j

and ε

j−j

the enthalpies associated with the diﬀerent type of bonds.

The partial enthalpy of the regular solution is

∂H

∂n

= H

+ ZΔ

+ n

)

(1.122)

− H

= ZΔc

(1.123)

Hence, the activity of the components in a regular solution can be represented

= c

exp



ZΔc



(1.124)

and, respectively,

= c

exp



ZΔc



(1.125)

Then from Eqs. (1.118), (1.124) and (1.125) we arrive at the relation between

the surface (boundary) concentration of the component and that of the bulk,

if both the bulk and the surface solutions are regular solutions:

exp



ZΔc



exp





(γ

−γ

)

⎡

⎣

exp





exp



ZΔc



⎤

⎦

(1.126)

where Δ

, Z

are the heat of mixing and the coordination number, respec-

tively, at the grain boundary.

Let us apply this result to some special situations.

1. No diﬀerence between the bulk and boundary solution with regard to the

heat of mixing and the coordination number; the partial areas of the diﬀerent

species are equal as well:

=Δ

= Z (1.127)

Then

exp



2ZΔ

+ c

− 1)



1 − c

+ Bc

exp



2ZΔ

+ c

− 1)



(1.128)

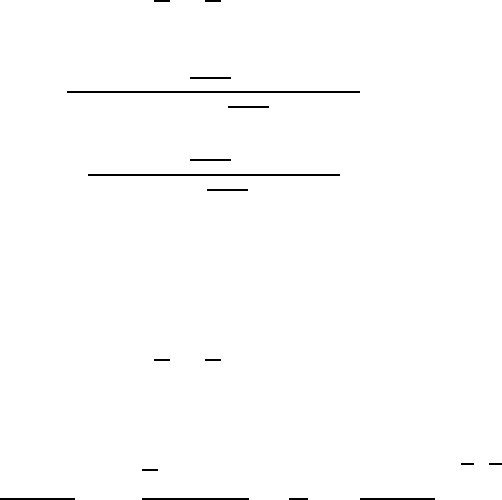
34 1 Thermodynamics of Grain Boundaries

Obviously, the relationship (1.128) is valid over the whole concentration range.

2. Ideal bulk solution but regular boundary solution

Δ=0

= 0 (1.129)

Then

exp



(2c

− 1)



1 − c

+ Bc

exp



(2c

− 1)



(1.130)

In the form

exp



(2c

− 1)



1+Bc

exp



(2c

− 1)



(1.131)

it is known as the Fowler-Guggenheim isotherm.

3. Ideal bulk solution and regular surface (boundary) solution; the areas of

the species at the boundary are diﬀerent:

Δ=0

= 0 (1.132)

=

In this case

= c

exp



−



exp



(γ

− γ

)





exp





(1.133)

1.2.6 Statistical Analysis of the Adsorption on Internal

Interfaces in Solids

As mentioned above, the thermodynamic description of grain boundaries is

based on the experiment, on the analysis of the experimentally obtained de-

pendencies of the surface tension on pressure and concentration of the compo-

nents. By contrast, for the statistical analysis of the problem model concepts

must be invoked. A detailed statistical analysis of the adsorption at internal

interfaces in solids, including grain boundaries, is given in [27].

Let us consider the equilibrium in the system: bulk solution - interface solu-

tion (more speciﬁcally, the interface is the grain boundary). We shall restrict

our consideration to binary systems. To describe equilibrium in the bulk so-

lution - grain boundary solution system, the isobaric-isothermal potential G

was calculated via the Gibbs canonical distribution:

G = −kT ln

Z (1.134)

1.2 Thermodynamics of Surfaces 35

Since for the system under consideration the partition function

Z =

Z (of the

bulk solution) ·

Z (of the grain boundary solution), then

Z = w

·w



















−





exp



−





(1.135)

Here

and

are the partition functions for one atom of the ﬁrst and second

components of the bulk solution;



and



are the same quantities for the

grain boundary solution; N

and N



and N



are the numbers of atoms

of the ﬁrst and second kind in the bulk and the grain boundary solution; w

and w

are the corresponding conﬁgurational (permutation) probabilities; U

and U

are the heats of transfer of atoms of the ﬁrst and second kind from the

bulk solution into the grain boundary solution. The equilibrium distribution

of the impurities between the bulk and the grain boundary corresponds to

a minimum of the thermodynamic potential G of the system, that is to say

either the corresponding partial derivatives is equal to zero, in other words

the chemical potentials of the impurity atoms in both solutions are the same.

This minimum is usually found from the constancy condition either for the

number of solvent atoms or for the number of sites.

One can see that the statistical approach allows considerable freedom.

Firstly, it is associated with the choice of the constants for the determina-

tion of a chemical potential. Let us discuss this problem in greater detail.

Assume that g

and g

are the number of sites for the atoms of the ﬁrst and

second kind in the bulk solution. If the atoms form a disordered substitutional

solid solution the values of g

and g

are indistinguishable; the total number

ofsitesinsuchasolutionisg = g

+ g

and it is just this quantity that ap-

pears in the statistical calculations for both atoms of the ﬁrst and the second

kind. However, if the atoms form an interstitial solid solution (or an ordered

substitutional solid solution) the values g

and g

appear separately.

Let g



and g



be the number of sites for the atoms of the ﬁrst and second

kind in the boundary solution. For the disordered substitutional solid solution

the sum g



+ g



= g

= const. appears as before in the calculations.

Let us postulate that the number of sites in the boundary solution is con-

stant, in other words



+ g



= g

= const. (1.136)

Notice that for the bulk solution this condition need not be satisﬁed. As an

example, if the components form a substitutional solution in the grain (in

the bulk), whereas at the grain boundary there is an interstitial one, a non-

compensated transfer of impurity atoms from the bulk to the grain boundary is

possible. Vacant lattice points should appear in this instance. Let us consider,

however, an equilibrium concentration of vacancies in the bulk (N

= N

Then the vacant lattice points will disappear and g = const. (We assume,

also, that the value of N

does not depend on the content of the impurities

in the solution.)

36 1 Thermodynamics of Grain Boundaries

Finally, we assume that the following conditions are always met:

+ N



=const.

+ N



= const. (1.137)

With regard to the conditions mentioned above, the thermodynamic situation

is deﬁned by the type of bulk and boundary solution: substitutional or inter-

stitional.

If the bulk and boundary solutions are disordered substitutional solid solu-

tions, the following conditions will be true:

+ N

= N =const.



+ N



= N

= const. (1.138)

This means that there is no uncompensated transfer of atoms from the bulk

solution to the boundary: if the impurity atoms transfer to the boundary the

solvent atoms come back to the bulk.

Note also that in this case g = N

. It should be stressed that there

are no conditions N

=const. or N



= const. which are commonly employed

in the course of the determination of the chemical potential.

If there is a substitutional solid solution in the bulk and an interstitial one

at the boundary, then, as already noted, the non-compensated transfer of

impurity atoms is possible and the following conditions will be valid:

=const.



= const. (1.139)

i.e. the solvent atoms occupy the lattice points of corresponding lattices and

they (the atoms) can change only the sites between themselves.

Finally, if both solutions are interstitial solutions, the number of the sites

is constant only if:

=const.



= const. (1.140)



=const.

So, the following four situations can be considered:

1. Both bulk and boundary solutions are disordered substitutional solid

solutions:

g =const.

= const. (1.141)

1.2 Thermodynamics of Surfaces 37

The sites of the solvent and the impurity atoms in the bulk and grain

boundary solutions (g

and g



and g



, respectively) are indistin-

guishable. Moreover,

+ N

= N =const.andN



+ N



= N

= const. (1.142)

2. There is a substitutional solid inside the grain body and an interstitial

solid solution at the boundary:

=const.; g



=const.; g



= const. (1.143)

3. Both solutions are interstitial solid solutions:

=const.; g



=const.; g



= const. (1.144)

4. There is an interstitial solid solution in the bulk, whereas at the grain

boundary a substitutional solid solution is formed.

We will restrict our consideration to the ﬁrst and second situation but even

under this limitation the variety of possibilities is much larger than in the case

of adsorption at the solid-gas interface.

While the adsorption at free surfaces which occurs from gas and bulk so-

lution is obviously ideal, in the case of adsorption at grain boundaries new

possibilities arise since the solid solution is nonideal. It is nonideal not only

thermodynamically, because of the usual force interaction, but also because

of an “exchange” interaction caused by the crystalline order. Thus, one site

can be occupied by only one atom, etc. In principle, three situations are pos-

sible for each of the subsystems under consideration (the bulk solution, the

boundary solution).

The ﬁrst is realized when the number of particles is much smaller than the

number of sites, i.e. N  g; consequently, either the bulk solution (concen-

tration c  1) or the grain boundary solution (the degree of boundary ﬁlling

Θ  1) is dilute.

Then the permutation probability in this case is determined by the Boltz-

mann distribution

W =

(1.145)

The second possible situation is realized when each site of both the bulk and

the grain boundary solution can be occupied by not more than one particle

(n ≤ g) (in analogy to the Fermi-Dirac distribution)

W =

N!(g − N )!

(1.146)

38 1 Thermodynamics of Grain Boundaries

then c, Θ ≤ 1.

Finally, we come to the third possibility: each site can be occupied by an

inﬁnite number of particles (an analogue of the Bose-Einstein distribution)

W =

(g + N )!

g!N !

(1.147)

As a result of possible situations for adsorption at internal interfaces in

solids, in particular at grain boundaries, largely exceeds the diversity of situ-

ations for adsorption at solid-gas interfaces.

Let us comment on the derivation of the adsorption isotherm. We are look-

ing for the minimum of the isobaric-isothermic potential by setting the partial

derivative ∂G/∂N

equal to zero under the boundary conditions given in Ta-

ble 1.1. Since N

+ N



= const., it follows that ∂/∂N

= −∂/∂N



etc. We

assume also that U

=0andU

= U , in other words, the adsorption heat of

the matrix component is zero: it means that only the solute atoms segregate

at the grain boundary.

If the phase has diﬀerent types of sites — which is typical for ordered solu-

tions, and consequently, which is particularly important for grain boundaries

— it is necessary to take into account not only the kinds of atoms but also

their number and sites of each type. For example, if there are two distinguish-

able kinds of sites α and β, the number of matrix atoms at the sites of the ﬁrst

kind is n

and so on. Then the permutation probability should be written as

+ N



+ N



instead of

+ N

For the substitutional solid solution the concentration of solute atoms in the

bulk solution c and the part of occupied sites in the boundary solution Θ can

be deﬁned in the natural way: c = N

/g,Θ=N



. For the interstitial

boundary solution Θ = N



Let us consider, as an example, the isotherm in a system, where both bulk

and boundary solutions are concentrated and in the boundary solution each

site can be occupied by one particle

Z =

(g − N

)!N

· (Z

)

· (Z

)

− N



)!N



·(Z



)





)



· exp







(1.148)

Since N

+ N



=const.,N

+ N



=const.,N

+ N

= g=const.

Z =

)





·(Z



)



· (Z



)



exp







(1.149)

1.2 Thermodynamics of Surfaces 39

TABLE 1.1

Diﬀerent Variants of the Isotherms

No. Bulk solution Surface solution

Conditions W Conditions W

2 g

substitutional g!/N

!/N

! substitutional g



4 g =const. g

=const. g

!/N





5(g

+ N



)!/g



7(g + N

)!/g!N

9 substitutional g

! substitutional

11 g = N

+ N

g!/N

! g



=const. (g



)



12 N

=const. g



=const. g



!/N



!(g



− N



13 N

=const. N



=const. (g



+ N



)!/g



16 (g + N

)!/g!N

Therefore, taking Stirling’s approximation, and the obvious relations

∂

∂N

= −

∂

∂N



= −

∂

∂N

∂

∂N



(1.150)

we get



∂ ln Z

∂N



g,g

=const.

=lnN

− ln N

− ln Z

+ln Z

+ln N



− ln N



+ln Z



− ln Z



−

= 0 (1.151)

With the notations

c = N

/g, Θ=N



and

B =(Z





)exp(U/kT)

we have

g − N

− ln

− N



=ln







exp (U/kT)



and thus



− 1



− ln



− 1



=lnB

40 1 Thermodynamics of Grain Boundaries

and ﬁnally

Θ=

1 − c + Bc

(1.152)

This result coincides with the Zhuchovitskii-McLean isotherm [23, 25]. Ne-

glecting the term “c” in the denominator, we obtain the Langmuir isotherm:

Θ=

1+Bc

(1.153)

For c  1andbc  1 both equations give the Henry isotherm.

The coeﬃcient b, which is proportional to exp(U/kT), consists in fact of

the solubility, more correctly, the ratio, of the impurity solubilities at the

grain boundary and the bulk (c



). Actually, the heat of adsorption, or the

heat of transfer of the impurity atom from the bulk to the grain boundary

U, is equal to the diﬀerence between the heat for dissolving it in the bulk q

and that for dissolving it at the grain boundary q

(if as zero energy level is

taken the energy of the atom in a phase, which is in equilibrium with both

our solutions, for example, in the gas phase). So, c



∼ exp [(q − q

) /kT] ∼

exp [U/kT] ∼ B. Conceptually, the same result was obtained by McLean, since

in his derivation U = E − e,whereE is the energy of dissolution in the bulk,

and e is the energy of dissolution in the grain boundary.

The last group of isotherms describes the situation when each site in the

interface (grain boundary) can be occupied by a number of particles.

For concentrated substitutional bulk and boundary solutions, in accordance

with the procedure elaborated above, we get:

Z =

)

+ N



·(Z



)





)



exp







(1.154)

+ N



=const.; g =const.

+ N



=const.; g

= const. (1.155)

+ N

= g =const.

and

Θ=

1 − c − Bc

(1.156)

As mentioned above Θ = Γ/Γ

, where Γ is the adsorption and Γ

is the

number of sites. In the example considered, it is possible that Γ > Γ

, and,

consequently, Θ > 1 and even, under certain conditions, it is possible that

Θ →∞(Table 1.2).

The expression (1.156) is an analogue of the multilayer adsorption, other

1.2 Thermodynamics of Surfaces 41

TABLE 1.2

Adsorption isotherms

No. Isotherms Restrictions

1 Bc c  1

2 Bc/(1 + Bc) c  1

3 Bc/(1 − Bc) c  1

4 Bc/(1 − c)Θ 1orc  (1 + B)

−1

5 Bc/(1 − c + Bc c ≤ 1orΘ≤ 1

6 Bc/(1 − c − Bc c ≤ (1 + B)

−1

or c

+ c



≤ 1

10 B



c exp(−c) c  1

11 B



c/[exp(c)+Bc] c  1

12 B



c/[expc) − Bc] c  1

13 B



c Θ  1orc  B

−1

14 B



c/(1 + B



c) c ≤ 1orΘ≤ 1

15 B



c/(1 − B



c) c ≤ B

−1

or c



≤ 1

Notes:

The numbering of isotherms in Table 1.1 is consistent with Table 1.2.

B = Z



exp(U/kT)/Z



= B

exp(U/kT)



= Z



exp(U/kT)/Z

= B



exp(U/kT)

and c



are the solubility of impurity atoms in the bulk (grain) and

at the boundary

B = c



than in the BET (Brunauer, Emmet, Teller) version, where two types of sites

with two diﬀerent heats of adsorption were introduced. There is one heat of

adsorption for each adsorption layer in the example considered (Eq. (1.156)).

Such a situation was considered by Langmuir in 1918

Θ=

1 − Bp

(1.157)

It is obvious that B = p

−1

,wherep

is the pressure of the saturated vapor.

When p → p

,ΘandΓ→∞, then condensation occurs.

Thus far we have taken into account the degrees of freedom associated with

the type of the bulk and boundary solutions. We also assumed that the grain

boundary is homogeneous, with regard to the adsorption sites, and that there

is an interaction between the adsorbed atoms. The further development of ad-

sorption theory should consider the eﬀects mentioned. Some of the adsorption

isotherms with interaction (both in the bulk and the boundary solution) were

considered above (Eqs. (1.126)–(1.133)). Now we would like to show how this

problem can be solved in the statistical approach. The consideration will be

given in the Bragg-Williams approximation.

The expression for the statistical sum of the system can be obtained by mul-

tiplying the right-hand side of Eq. (1.127) by exp



−ZΔ(N



) H

/ (2g

kT)

