Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

12 1 Thermodynamics of Grain Boundaries

where n

is the atomic density of the i-th component. The correlation between

the surface excesses according to Hart





and according to Gibbs





is given by

= M

+ m



V −





(1.47)

We would like to remind the reader once again that on the one hand, the

choice of a particular method is governed by the speciﬁc conditions of the

problem and, on the other hand, it is also a matter of convenience.

Let us return to Eq.(1.17). For the surface parameters it reads

dΩ

= −pdV

− S

dT −



dμ

+ γd

A (1.48)

Then, comparing Eqs. (1.41) and (1.48) one can get

Adγ = −S

dT −



dμ

+ V

dp (1.49)

For the speciﬁc values s

= S

A,Γ

= N

A, v

= V

A, Eq. (1.49) acquires

the form

dγ = −s

dT −



dμ

+ v

dp (1.50)

This is the well-known Gibbs equation, which connects the change in surface

tension with the variations in temperature, pressure and chemical potentials

of the bulk phases. The relation (1.50) holds for any surface which is in equi-

librium with the volumes, divided by it.

The Gibbs equation is equally applicable to adsorption at interphases and

to adsorption at grain boundaries, but the grain boundary degeneracy results

in several important distinctions between adsorption at grain boundaries and

at interphases.

A system with an interphase has, at least, two phases, and the number f of

thermodynamic degrees of freedom in such a system, according to the Gibbs

rule of phases, is

f = k +2− p (1.51)

where p is the number of coexisting phases and k the number of components.

The number of diﬀerentials on the right-hand side of the adsorption Eq. (1.50)

is k +2>k; therefore, not all of them are independent, so it is not possible

to calculate excess surface quantities by direct diﬀerentiation of the surface

tension with respect to a corresponding variable. In order to represent surface

excesses in the form of a partial derivative of the surface tension with respect

to one of the variables two additional links are required. One of them can be

the method of calculation of the surface excesses. So, in the Gibbs method, in

1.2 Thermodynamics of Surfaces 13

alocalsense,V

= 0, and the number of diﬀerentials on the right-hand side

of Eq. (1.50) decreases to k + 1. Then Eq. (1.50) assumes the form

dγ = −s

dT −



i=1

dμ

(1.52)

and for T =const.

dγ = −



dμ

(1.53)

This is the most frequently used form of the Gibbs adsorption equation.

As mentioned before, the diﬀerential relations between the surface excesses

should be insensitive to the position of dividing surface; nevertheless, the

values of surface excess quantities depend on it. Let us illustrate this by means

of Eq.(1.53). Assume there are two dividing surfaces A

and A

,andthe

adsorption by them is Γ

and Γ



, respectively. Obviously,

=Γ



−



− c



Δ (1.54)

where c

, c

are the bulk concentrations of the i-th component in the bulk

phases, and Δ is the distance between the dividing surfaces. The sign of Δ

depends on the position with respect to the phases α and β:ifA

is nearer

to the phase α than A

then Δ is positive (Δ > 0). If the temperature of the

system is constant, the Gibbs-Duhem equation is valid for each of the phases:

dp =Σc

dμ

; dp =Σc

dμ

(1.55)

and the equation for the phase equilibrium acquires the form





− c



dμ

= 0 (1.56)

Rewriting Eqs. (1.53) and (1.54) in terms of Eq. (1.56) we get

dγ = −





dμ

(1.57)

As can be seen, Eq. (1.52) does not depend on the position of an arbitrary

dividing surface, as we intended to prove.

A further relation can be found by choosing the position of the dividing

surface. This is usually done in such a way that the adsorption of one of the

components (as a rule, of the solvent) will be equal to zero.

Guggenheim and Adam [8] suggested placing the dividing surface between

the transition layer and the bulk of the condensed phase. There is an impor-

tant advantage to such approach. If the second phase is liquid, in the case

mentioned above, the calculated values of the surface excesses coincide with

14 1 Thermodynamics of Grain Boundaries

the real concentrations, densities and so on in the surface layer. Let us ex-

press the diﬀerential of the chemical potential of one of the components, say

the ﬁrst one, and the diﬀerential of the surface tension as a function of the

diﬀerentials of the other components (Eqs. (1.56) and (1.53)):

dμ

= −



i=2



− c



dμ

− c

(1.58)

dγ = −



i=2



− Γ

− c



dμ

(1.59)

The parameters Γ

(1)

=Γ

− Γ



− c





− c



are called the relative

Gibbs adsorptions. Contrary to the adsorptions Γ

, the relative adsorptions

are independent of the position of the dividing surface. Γ

(1)

is the adsorption

of the i-th component attributed to the dividing surface, where Γ

=0(Fig.

1.1).

For binary systems with an interphase such an approach makes it possible

to express conveniently the adsorption (of the second component) Γ

Γ=−

dγ

dμ

= −

dγ

(1.60)

where a is the activity.

The relationship (1.60) is used very often for adsorption at the grain bound-

aries, neglecting that this is a diﬀerent situation.

1.2.4 Gibbs Thermodynamic Method Applied to Grain

Boundaries

The title of this chapter reﬂects the essential thermodynamic distinctions

between grain boundaries and interphases. In turn these distinctions are con-

nected with the above-mentioned property of grain boundaries — they divide

similar phases. The ﬁrst distinction consists of the fact that the surface ex-

cesses of any extensive value for the grain boundary are independent of the

choice of the Gibbs dividing surface. Actually, inasmuch as the regions α and

β, divided by the grain boundary, are occupied by the common phase, the

bulk densities m

and m

of the extensive quantity M have the same value

= m

. In accordance with Eq. (1.30), the surface excesses M

are

equal:

= M − Vm

(1.61)

and do not depend on the position of the dividing surface, i.e. on the parameter

ξ. Naturally, this is a physical result, and it is connected with the alternative

version of the Gibbs approach. For example, for the approach, which is deﬁned

1.2 Thermodynamics of Surfaces 15

by the condition Ω

= 0 (Eq. (1.44)), we obtain for grain boundaries

= M − m



V −



(1.62)

i.e. a value that does not depend on the parameter η, which is the analogue

of the parameter ξ. This is clearly demonstrated in Fig. 1.1.

The second peculiarity of grain boundary thermodynamics consists of the

fact that for a system with a grain boundary the number of degrees of freedom

by one is greater than for the interphase (see Eq. (1.51)).

Therefore, for a system with a grain boundary all diﬀerentials on the right-

hand side of the Gibbs equation (1.52) are independent; for a grain boundary

the Gibbs-Duhem equation does not impose any restrictions on the system,

due to c

= c

for all i (compare with the results of [9]). The surface excesses

of the grain boundaries are independent of the position of the dividing surface

and depend on the properties of the grain boundary only. The same can be

described more rigidly in terms of the method mentioned above. The surface

excesses can be determined by the Gibbs method as diﬀerences between a real

system, in which the surface is a certain transition layer between two phases,

and an ideal system, in which the phases are considered to be homogeneous

up to the plane of contact (Fig. 1.1a). For an interphase the excesses are obvi-

ously determined by the position of the imaginary surface, which divides two

homogeneous planes. In the case of the grain boundary (Fig. 1.1b), precisely

because the properties of the bulk on both sides of the boundary are the same,

the excess quantities are independent of the imaginary surface position and

have themselves an objective signiﬁcance.

Due to the availability of the additional degree of freedom a number of

unique possibilities arise. In particular, one can consider adsorption at grain

boundaries in a one-component system, which we shall call autoadsorption.

(There is no sense in considering such a problem for an interphase, inasmuch

as at constant temperature such a system is completely determined.) In this

case Eq. (1.52) takes the form [9]:

dγ = −s

dT − Γ

dμ (1.63)

The parameter Γ

has the meaning of an autoadsorption at grain boundaries

in pure material. Expressing μ through the thermodynamic characteristics of

the volume and taking into account that s

=Γ

,wheres

is the surface

excess of the entropy per atom at the surface, we get [9]:

dγ = −Γ



− s



dT − Γ

dp (1.64)

where s

istheentropyofoneatominsidethecrystal,Ω

is the atomic volume.

Hence



∂γ

∂p



= −Γ

(1.65)

16 1 Thermodynamics of Grain Boundaries



∂γ

∂T



= −Γ



− s



= −

(1.66)

where q is the speciﬁc heat of grain boundary formation and −q/T is the

speciﬁc surface excess of entropy.

From Eqs. (1.65) and (1.66) it is evident that it is in principle possible to

measure the autoadsorption and the surface excess of entropy.

For our evaluation we shall take Γ

=5·10

−14

mol/m

, which approximately

corresponds to the concept of the grain boundary as an undercooled liquid

layerofawidthof3atomicrows,Ω

(10

−5

/mol). Assuming that γ(p)is

linear, a variation of pressure from 0 to ∼2.5 GPa gives a change of 0.1 J/m

which is comparable with the absolute value of γ (0.3-0.5 J/m

1.2.4.1 Grain Boundary Excess Free Volume —

Direct Thermodynamic measurement

Eqs. (1.63)–(1.66) form the theoretical basis of the direct experimental mea-

surements of grain boundary excess free volume (BFV).

BFV along with surface tension belongs to the major thermodynamic prop-

erties of grain boundaries. It controls to a large extent the grain boundary

diﬀusivity, grain boundary mobility, vacancy generation during grain growth

and the behavior of the system with grain boundaries under mechanical load-

ing. The value of the BFV deﬁnes the force which would like to “squeeze”

grain boundary out of a polycrystal. This eﬀect is especially pronounced in

ﬁne grained and nanocrystalline materials, in this ﬁlms on substrate [11]–[15].

Unfortunately, until quite recently we were forced to contend with results of

computer simulation, which, in its turn, is strictly limited by grain boundaries

in the vicinity of special misorientation.

Some experimental attempts were undertaken to determine the BFV

[16, 17]. Meiser and Gleiter [16] measured the change of misorientation for

grain boundary energy cusps by applying a hydrostatic pressure of 7 ·10

Pa.

Merkle et al. [17] measured the BFV by HRTEM observations of the lattice

parameter change in the vicinity of the grain boundary. The value of BFV av-

eraged over all measurements carried out is in the range of 1

−12

−10

It should be stressed, however, that all estimates are based on models since

they have to rely on assumptions of the grain boundary width, which is un-

known.

As shown above, Eqs. (1.63)–(1.66) make it possible, in principle, to mea-

sure correctly the grain boundary excess free volume. To “realize” these equa-

tions the pressure dependence of the grain boundary surface tension should

be known.

The major idea of the method put forward in [18] can be understood from

Fig. 1.2. The tricrystal with grain boundaries GB1, GB2, GB3 is annealing

under high hydrostatic pressure. The change in grain boundary surface ten-

sion has to be reﬂected in the change in the angles at the tip of the triple

1.2 Thermodynamics of Surfaces 17

GB3

GB2

GBI

GB3

GB2

GBI

(a) (b)

GB3

GB2

GBI

GB3

GB2

GBI

GB3

GB2

GBI

GB3

GB2

GBI

(a) (b)

FIGURE 1.2

(a) Grain boundary geometry to determine the BFV: the grain boundary sys-

tem with triple junction attains an equilibrium conﬁguration at the notches

introduced from the lateral surfaces of the tricrystal. (b) SEM image of inves-

tigated grain boundary system after annealing [18].

junction.

The proposed method was realized in specially grown tricrystals where the

triple junction is formed by two high-angle grain boundaries GB1 and GB2

with equal grain boundary surface energy γ

= γ

= γ (Fig. 1.2). The third

grain boundary has to be a low-angle grain boundary whose surface energy γ

can be calculated according to the Read and Shockley approach [19]. The sys-

tem in Fig. 1.2 is homogeneous through the thickness of the tricrystal, i.e. the

triple junction line is rectilinear and runs perpendicular to the diagram plane.

Since through the thickness all three grain boundaries extend perpendicular

to the diagram plane, the conﬁguration of the grain boundary system in Fig.

1.2 is quasi-two-dimensional. So, the motion of the grain boundary system is

similar to the motion of a grain boundary system with a triple junction (see

Chapter 4), until GB1 and GB2 arrive at the notches (Fig. 1.2). Boundary

motion will cease, and force equilibrium at the triple junction will be estab-

lished. In this equilibrium the contact angle 2θ reﬂects the balance between

the energy of boundaries GB1, GB2 and GB3 at the given temperature and

pressure

2γ cos θ = γ

(1.67)

Eqs. (1.65) and (1.67) gives us the relationship between the contact angle and

the hydrostatic pressure

∂γ

∂p

2γ

∂θ

∂p

sinθ +

∂γ

∂p

2cos θ

(1.68)

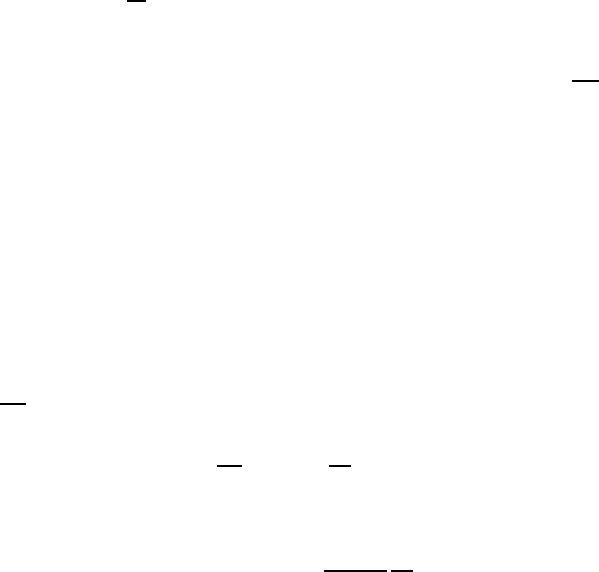
18 1 Thermodynamics of Grain Boundaries

In Eq. (1.68) θ,

∂θ

∂p

and γ are experimentally measured quantities. (The grain

boundary surface tension γ can be found from Eq. (1.67), if the surface tension

of the low angle boundary is measured or calculated.) In our consideration we

neglect the inﬂuence of the torque terms. To deﬁne the derivative



∂γ

∂p



the

following approach was used. According to Read and Shockley [19] a low-angle

grain boundary can be represented by a periodic arrangement of lattice dislo-

cations. In particular, a low-angle twist grain boundary is represented by at

least two sets of screw dislocations. The elastic energy of a screw dislocation

(apart from the dislocation core energy) is not aﬀected by the hydrostatic

pressure since a screw dislocation represents a state of pure shear. The en-

ergy of the dislocation core does not exceed 10% of the total energy of the

dislocation. The eﬀect of the hydrostatic pressure on the lattice constant and,

therefore, on the dislocation and low-angle boundary energy is less than 10%.

It can, therefore, be assumed that the energy of a low-angle twist grain bound-

ary does not change with an increase of hydrostatic pressure.

If the grain boundary GB3 in Fig. 1.2 is a low-angle twist boundary and



∂γ

∂p



∼

0, Eq. (1.68) can be rewritten as



∂γ

∂p



= γ



∂θ

∂p



· tan θ (1.69)

and BFV can be expressed as

Vgb

= γ

sin θ

2cos

∂θ

∂p

(1.70)

BFV was measured for two 40

◦

asymmetrical grain boundaries: 111 and

110. The experiments were carried out on high purity aluminum (99.999%)

[18]. Fig. 1.3 shows the geometrical conﬁguration of the investigated tricrys-

tals for 111 and 110 tilt boundaries. The two asymmetrical 40

◦

111 of

◦

110 tilt grain boundaries (GB1 and GB2) were superimposed by a rota-

tion around the axis perpendicular to the grain boundary plane by an angle

Ψof2

◦

. The third grain boundary (GB3) was, therefore, a low-angle twist

boundary with rotation angle of 4

◦

and the rotation axis 110.Thesam-

ples were annealed at 630

◦

C for 60 min under a hydrostatic pressure up to

12.7 kbar (grain boundary system 111) and 10 kbar grain boundary system

110) [18, 20]. The surface tension of 4

◦

110 twist grain boundary was deter-

mined by molecular dynamic simulation [20] (Fig. 1.4). This small deviation

does not change perceptibly the properties of high-angle grain boundaries;

however, for the energy of the low-angle grain boundary is might be essential.

The relation γ vs. angle (Fig. 1.4) of misorientation allows us to determine the

energy of the low-angle twist boundary for each speciﬁc sample. That is why

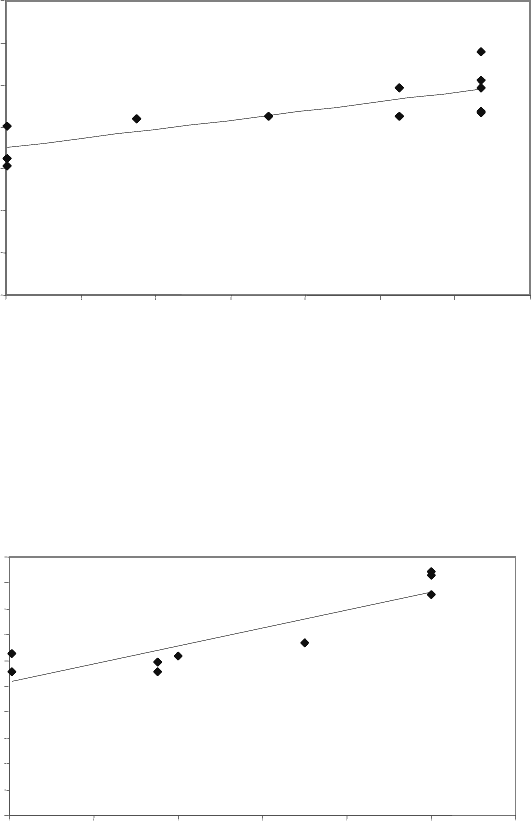
in Figs. 1.5 and 1.6 the measured pressure dependence of the surface tension

γ is presented. To check the results obtained the pressure dependence of the

equilibrium vertex angle θ was measured for a grain boundary system of two

1.2 Thermodynamics of Surfaces 19

FIGURE 1.3

Geometry of tricrystals used in experiment [18].

FIGURE 1.4

Misorientation dependence of low-angle 110 twist grain boundary computer

simulation [20].

20 1 Thermodynamics of Grain Boundaries

40° <111>boundary

0.3

0.35

0.4

0.45

0.5

0.55

0.6

0.65

02468101214

pressure, kbar

[J/m

]

40° <111>boundary

0.3

0.35

0.4

0.45

0.5

0.55

0.6

0.65

02468101214

pressure, kbar

[J/m

]

[J/m

]

FIGURE 1.5

Pressure dependence of grain boundary surface tension γ for 40

◦

111 tilt

boundary [18, 20].

39°<110> boundary

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

024681012

pressure, kbar

[J/m

]

39°<110> boundary

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

024681012

pressure, kbar

[J/m

]

FIGURE 1.6

Pressure dependence of grain boundary surface tension γ for 39

◦

110 tilt

boundary [18, 20].

1.2 Thermodynamics of Surfaces 21

0 2 4 6 8 10121416

115

116

117

118

119

120

121

122

[°]

pressure, kbar

0 2 4 6 8 10121416

115

116

117

118

119

120

121

122

[°]

pressure, kbar

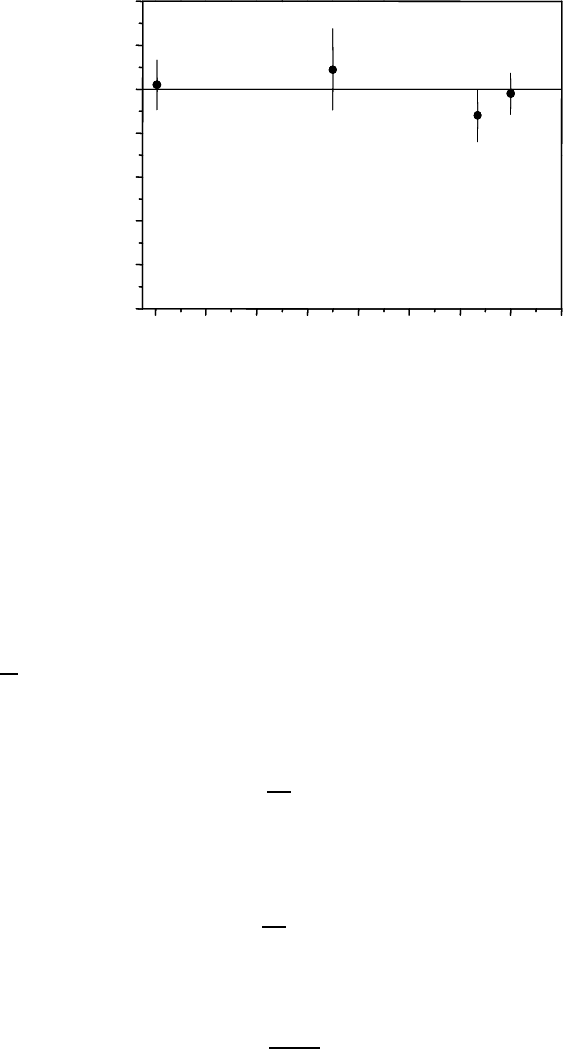
FIGURE 1.7

Pressure dependence of grain boundary surface tension γ of high-angle bound-

aries: two 40

◦

111 grain boundaries and 80

◦

111 tilt boundaries [18].

◦

111 tilt grain boundaries as GB1 and GB2 and an 80

◦

111 tilt boundary

as GB3. Due to crystal symmetry 80

◦

111 corresponds to −40

◦

111,andthe

grain boundary energy of GB3 should be the same as the energy of GB1 and

GB2. The results of the measurements are shown in Fig. 1.7. The measured

angle was about 120

◦

in the whole pressure range and, what is of importance,



∂θ

∂p



= 0. Below are given the value of the BFV for 40

◦

111 tilt grain

boundary and 39

◦

110 tilt grain boundary extracted from the experimental

data (Figs. 1.5 and 1.6) in accordance with Eqs. (1.65) and (1.68) [18, 20]

110 :Γ

= −Ω

−1



∂γ

∂p



= −1.35 · 10

−5

mol/m

(1.71)

= −Γ

=1.35 · 10

−10

± 0.6 · 10

−10

111 :Γ

= −Ω

−1



∂γ

∂p



=0.55 · 10

−5

mol/m

(1.72)

= −Γ

=0.55 · 10

−10

± 0.13 · 10

−10

110

111

=2.5 (1.73)