Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.

214 3 Grain Boundary Motion
0 200 400 600 800 1000
x [µm]
0
200
400
y
[
µ
m
]
0 200 400 600 800 1000
0
200
400
x [µm]
y [µm]
0 200 400 600 800 1000
x [µm]
0
200
400
y
[
µ
m
]
0 200 400 600 800 1000
0
200
400
x [µm]
y [µm]
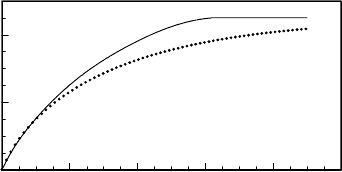
FIGURE 3.41
Comparison between experimental data (solid line) and calculated shape (dot-
ted line) disregarding segregation.
can be successfully fitted by Eq. (3.149) using only x
∗
as a free fit parameter
(Fig. 3.42).
The same holds for the reversed-capillary technique. Any attempt to fit
the shape by assuming a freely moving boundary fails, but good agreement
between experiment and theory can be observed when impurity drag and thus
different mobilities are taken into account (Fig. 3.43) [241].
As mentioned above, the shape of a moving grain boundary is a new source
of information on grain boundary migration. One example is given in Fig. 3.44,
where the value of the critical distance x
∗
, normalized by the driving force
(in terms of the quarter-loop width a) is plotted vs. the impurity content. In
accordance with the L¨ucke-Detert theory [193] the critical velocity v
∗
(and
rigidly bound to it the position of the critical point x
∗
on the quarter-loop) is
determined by the balance between the maximum force of interaction of the
impurity atoms with the boundary and the force, which is imposed by the en-
ergy dissipation caused by boundary motion across the matrix. The difference
in the impurity drag for grain boundaries in samples with different amount
of impurities is caused by the adsorption of impurities at the grain boundary.
According to theory the velocity should decrease proportionally to the inverse
of the concentration of adsorbed atoms. Therefore, x
∗
should increase with
decreasing impurity content, as observed qualitatively (Fig. 3.44) [244]. How-
ever, a linear relation between the inverse of the impurity concentration and
v
∗
, i.e. x
∗
, is not observed over the whole concentration range, which indicates
a more complicated interaction of adsorbed atoms with the grain boundary.
In such a case x
∗
/a should increase more strongly with decreasing impurity
content than linearly. This tendency is indeed observed (Fig. 3.44).
Evidently, even in very — although not perfectly — pure metals there is
no agreement between the experimentally observed and calculated shape of
a moving grain boundary, if the impurity influence is not taken into account.
This has to be kept in mind to avoid serious misinterpretation when evaluating
© 2010 by Taylor and Francis Group, LLC
3.4 Measurement of Grain Boundary Mobility 215
0 200 400 600 800 1000
x [µm]
0
200
400
y
[
µ
m
]
0 200 400 600 800 1000
0
200
400
x [µm]
y [µm]
(a)
0 200 400 600 800 1000 1200
x [µm]
0
250
500
750
y
[
µ
m
]
0 200 400 600 800 1000
0
250
750
x [µm]
y [µm]
(b)
500
1200
0 200 400 600 800 1000
x [µm]
0
200
400
y
[
µ
m
]
0 200 400 600 800 1000
0
200
400
x [µm]
y [µm]
(a)
0 200 400 600 800 1000 1200
x [µm]
0
250
500
750
y
[
µ
m
]
0 200 400 600 800 1000
0
250
750
x [µm]
y [µm]
(b)
500
1200
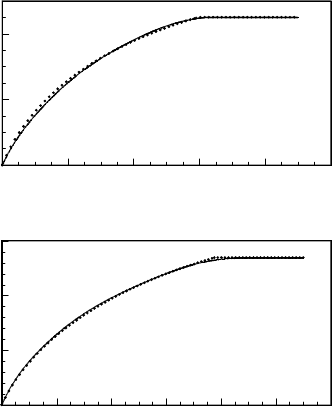
FIGURE 3.42
Experimentally observed (solid line) and calculated (Eq. (3.149), dotted line)
grain boundary shape for Al with an impurity content of (a) 1.0 ppm (b)
3.6 ppm (quarter-loop technique).
© 2010 by Taylor and Francis Group, LLC
216 3 Grain Boundary Motion
(a) (b)
(c)
0
0
0
0
00
500
500
500
1000
1000
1000
500500
500
10001000
1000
1500
15001500
1500
1500
1500
x [µm]
x [µm] x [µm]
y [µm]
y [µm]
y [µm]
(a) (b)
(c)
0
0
0
0
00
500
500
500
1000
1000
1000
500500
500
10001000
1000
1500
15001500
1500
1500
1500
x [µm]
x [µm] x [µm]
y [µm]
y [µm]
y [µm]
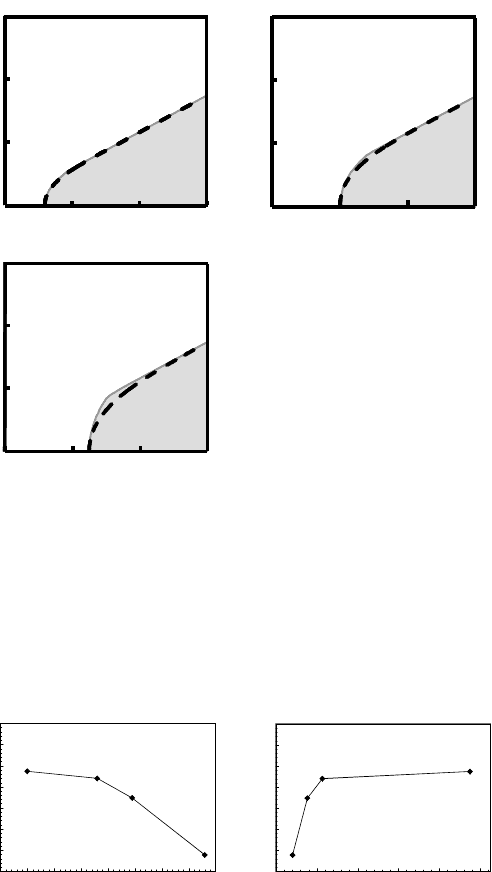
FIGURE 3.43
Experimentally observed and calculated shape accounting for drag effect:
(shaded area), neglecting the drag effect (dashed line) (Fe-3%Si, reversed-
capillary technique): (a) theoretically predicted grain boundary shape; (b)
accounting for drag effect; (c) without regard to drag effect.
0 1 2 3 4 5 6 7 8
impurity content [ppm]
0.58
0.6
0.62
0.64
0.66
0.68
x
*
/
a
0
12 534 67
c [ppm]
0.60
0.64
0.68
0.56
x*/a
(a)
0.05 0.25 0.45 0.65 0.85 1.05
inverse impurity content [1/ppm]
0.58
0.6
0.62
0.64
0.66
0.68
x
*
/
a
0.60
0.64
0.68
0.56
.05
c
-1
[1/ppm]
0.25 0.45 0.65 0.85 1.05
(b)
0 1 2 3 4 5 6 7 8
impurity content [ppm]
0.58
0.6
0.62
0.64
0.66
0.68
x
*
/
a
0
12 534 67
c [ppm]
0.60
0.64
0.68
0.56
x*/a
0.60
0.64
0.68
0.56
x*/a
(a)
0.05 0.25 0.45 0.65 0.85 1.05
inverse impurity content [1/ppm]
0.58
0.6
0.62
0.64
0.66
0.68
x
*
/
a
0.60
0.64
0.68
0.56
.05
c
-1
[1/ppm]
0.25 0.45 0.65 0.85 1.05
c
-1
[1/ppm]
0.25 0.45 0.65 0.85 1.05
(b)
FIGURE 3.44
Dependence of critical point x
∗
/a on (a) impurity content; (b) reciprocal im-
purity content.
© 2010 by Taylor and Francis Group, LLC

3.5 Experimental Results 217
experimental mobility data.
3.5 Experimental Results
3.5.1 Relation between Driving Force and Migration Rate
As elaborated in Sec. 3.1 the driving force for grain boundary migration is
always small compared to the thermal energy. Therefore, grain boundary mi-
gration is a drift motion following the trend to reduce the energy content of
the crystalline aggregate. A drift velocity, however, is always proportional to
the driving force, as derived in Sec. 3.1 (Eq. (3.6))
v = m
b
P
and the proportionality factor m is the grain boundary mobility
m
b
= v/P (3.151)
In accurate experiments relation (3.6) is unambiguously confirmed, most pre-
cisely for the motion of a planar grain boundary under the action of a magnetic
driving force (Fig. 3.45). In this case the grain boundary crystallography is
exactly defined and remains unchanged during boundary motion. Moreover,
the driving force can be precisely calculated and varied in a defined manner.
Also for the motion of curved grain boundaries Eq.(3.6) is obeyed (Fig. 3.46),
although for very small driving forces a deviation to lower migration rates
is observed. This deviation is likely to be due to drag effects (solute drag,
groove dragging) which necessarily have to show up when the driving force
tends to zero since no material is absolutely pure. A proportionality between
mean migration rate and elastically stored energy was even reported for grow-
ing grains in polycrystals (Fig. 3.47). Despite this conceptually necessary and
experimentally confirmed relation (3.6) there have been reports in pertinent
literature which contended that Eq.(3.6) does not hold, rather
v ∼ P
n
(3.152)
with n 1 and as high as n = 12 would more adequately comply with
experimental results. The crucial experiment to prove this complication was
due to Rath and Hu [230]–[233] (Fig. 3.48), who conducted experiments on
aluminum bicrystals using wedge-shaped specimens (Sec. 3.4.2.1, Fig. 3.25a).
These results have worried the scientific community for many years since such
results cannot be understood from fundamental principles (Sec. 3.1) and also
preclude a determination of grain boundary mobility without further theoret-
ical treatment of relation (3.152). It can be shown, however, that the observed
© 2010 by Taylor and Francis Group, LLC

218 3 Grain Boundary Motion
0 100 200 300 400
p [J/m
3
]
0
0.1
0.2
0.3
0.3
0.2
0.1
0
v [mm/s]
0 100 200 300 400
P [J/m
3
]
0 100 200 300 400
p [J/m
3
]
0
0.1
0.2
0.3
0.3
0.2
0.1
0
v [mm/s]
0 100 200 300 400
P [J/m
3
]
FIGURE 3.45
Measured grain boundary migration rate vs. driving force of a flat boundary
in a bicrystal of Bi exposed to a magnetic field.
relation (3.152) is due to improperly conducted experiments and, therefore, a
misinterpretation of experimental data.
The experiments of Rath and Hu [230]–[233] were carried out on aluminum
in a hydrogen (reducing) atmosphere which strongly promotes grooving since
aluminum does not form a protective oxide layer on its surface under these con-
ditions. Also, they used a discontinuous method to measure the grain bound-
ary displacement with large intervals of annealing time. So, the experimental
results corresponded to an average displacement including a large number of
detachment-attachment processes of the moving boundary from its groove. In
this case [210, 225] the average boundary migration
v = lim
t→∞
,
t
0
v(q)dq
t
=
,
τ
0
v(q)dq
τ
(3.153)
where τ is the time between two consecutive detachments according to
Eq.(3.99). Since the principal mechanism of groove development in aluminum
is surface diffusion, the average grain boundary velocity is obtained by differ-
entiation of Eq. (3.96) (Sec. 3.3.6) and (3.153)
v =4PA
b
1
χ
3
−
1
6χ
4
ln
(1 + χ)
3
1+χ
3
−
1
χ
4
√
3
arc tan
2χ − 1
√
3
+
π
6
(3.154a)
where
χ =
Pδ
2γΘ
c
− 1
−1/3
(3.154b)
© 2010 by Taylor and Francis Group, LLC
3.5 Experimental Results 219
3
1
2
05 1510 20
v [10
-4
m/s]
P/
γ
[1/cm]
I
II
3
1
2
05 1510 20
v [10
-4
m/s]
P/
γ
[1/cm]
I
II
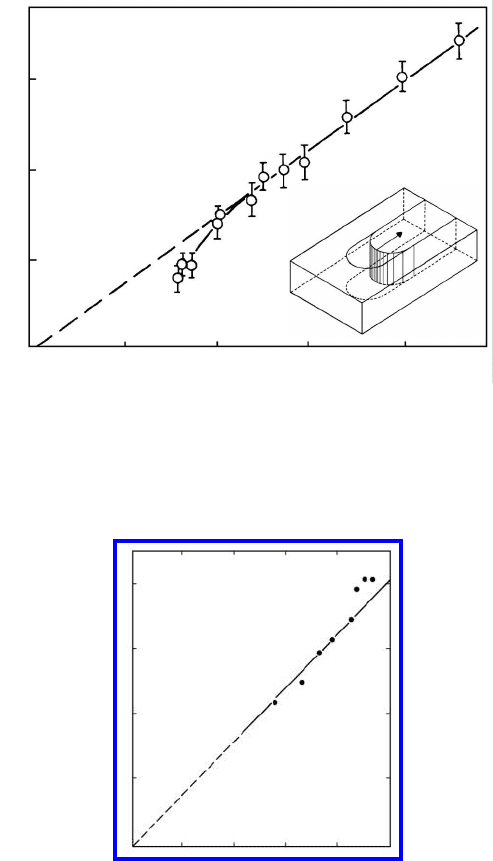
FIGURE 3.46
Measured grain boundary migration rate vs. reduced driving force of U -shaped
boundaries in Al bicrystals (half-loop technique).
0 0.8 1.6 2.5 3.3 4.2
7
14
21
28
0
P [J/mol unrecrystallized]
v/v
0
[s
-1
]
0 0.8 1.6 2.5 3.3 4.2
7
14
21
28
0
P [J/mol unrecrystallized]
v/v
0
[s
-1
]
FIGURE 3.47
Average growth rate (normalized by a constant v
0
) as a function of the driv-
ing force for a polycrystalline aluminum alloy containing 17 ppm Cu during
primary recrystallization at 125
◦
C [262].
© 2010 by Taylor and Francis Group, LLC

220 3 Grain Boundary Motion
n = 1.0
n = 1.5
n = 5.5
v [m/min]
10
-2
10
-17
10
-12
10
-7
P [J/m
3
]
10
0
10
5
10
1
10
2
10
3
10
4
10
8
10
7
10
6
10
-6
10
-1
10
-5
10
-4
10
-3
10
-2
10
2
10
1
10
0
P [MPa]
n = 12.3
n = 1.0
n = 1.5
n = 5.5
v [m/min]
10
-2
10
-17
10
-12
10
-7
P [J/m
3
]
10
0
10
5
10
1
10
2
10
3
10
4
10
8
10
7
10
6
10
-6
10
-1
10
-5
10
-4
10
-3
10
-2
10
2
10
1
10
0
P [MPa]
n = 12.3
FIGURE 3.48
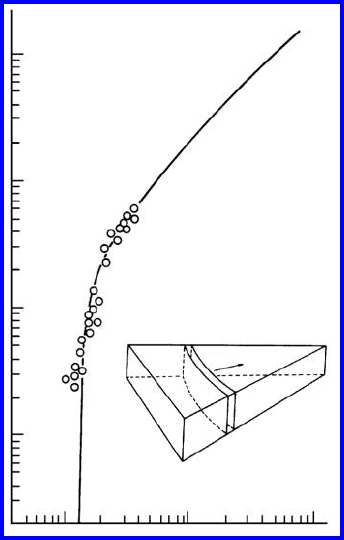
Boundary migration rate vs. driving force as reported by Rath and Hu [231]
for wedge-shaped Al bicrystals.
Correspondingly, the kinetics in the experiments mentioned are entirely con-
trolled by thermal grooving and groove dragging rather than by an intrinsic
relation between migration rate and driving force [225] (Fig. 3.49).
The concept derived in Sec. 3.3.6 provides a basis for formulating the re-
quirements to be satisfied by an experiment aimed at a physically correct
study of grain boundary motion. It is important to note that a necessary
condition [210] for grooving to be negligible is the magnitude of the criterion
ρ
ρ =
Pδ
γΘ
c
∼
=
Pδγ
s
γ
2
1 (3.155)
An analysis of this criterion applied to the series of experiments by Rath and
Hu [230]–[233] reveals the following scenario: driving force P = γ/R with
R =1.02 −0.2 cm, sample thickness 0.25 cm thick. Taking γ/γ
s
∼
=
0.3 [263],
one obtains for the beginning of motion ρ
∼
=
0.5 and at the end ρ
∼
=
4, i.e. only
toward the end can one expect a free motion of the boundary, while groove
dragging controls most of the experiments. In conclusion, the results obtained
do not pertain to free boundary motion.
Rath and Hu [230]–[233] surmised that the nonlinearity v ∼ P
n
was due to
impurity drag such that the boundary was in the transition regime between
loaded and free state (Sec. 3.3.2, Fig. 3.6). This is not feasible, however, since
the boundary will assume either the loaded or the free state, if the transition
is discontinuous, as observed experimentally (Fig. 3.7). Only for very small
© 2010 by Taylor and Francis Group, LLC
3.5 Experimental Results 221
10
-1
10
-2
10
-3
10
-4
10
2
10
3
10
4
P [J/m
3
]
v [cm/min]
A
B
10
-1
10
-2
10
-3
10
-4
10
2
10
3
10
4
P [J/m
3
]
v [cm/min]
A
B
FIGURE 3.49
Calculated v(P ) dependency (curve) in the presence of groove dragging. Sym-
bols are values reported by Rath and Hu (see Fig. 3.48).
© 2010 by Taylor and Francis Group, LLC

222 3 Grain Boundary Motion
impurity contents and driving forces is there a continuous transition from the
loaded state to the free motion state which, however, is limited to a small
driving force interval, much smaller than the driving force noted in the exper-
iments of Rath and Hu.
With the proportionality between migration rate and driving force being
unambiguously established, Eq.(3.151) can be applied to extract the grain
boundary mobility from grain boundary motion experiments and to determine
the influence of temperature, hydrostatic pressure, grain boundary crystallo-
graphy, chemical composition etc. on grain boundary mobility.
3.5.2 Kinetic Parameters of Grain Boundary Mobility
As evident from Sec. 3.1 grain boundary migration is a thermally activated
process. Thus, its kinetics follow an Arrhenius-type temperature dependence
v = v
0
exp
−
H
m
kT
(3.156)
Since the driving force is independent of temperature, the temperature de-
pendence of v is the temperature dependence of the grain boundary mobility
m
b
=
v
P
= m
0
exp
−
H
m
kT
(3.157)
where H
m
is the activation enthalpy of grain boundary migration and m
0
the
corresponding preexponential mobility factor. It is noted that
H
m
= E
m
+ pV
∗
(3.158)
(E
m
— activation energy) depends on the pressure p,whichcanbeusedto
determine the activation volume V
∗
(Sec. 3.5.4). However, for all practical
purposes grain boundary migration proceeds under a constant (ambient) pres-
sure.
Since most results referred to in the following were obtained for the mi-
gration of curved grain boundaries, we introduce for simplicity the reduced
mobility (see footnote in Sec. 3.4.3)
A
b
= m
b
· γ = A
0
exp
−
H
m
kT
(3.159)
For the half-loop geometry it can be obtained from the boundary velocity by
A
b
= va/2, for the quarter-loop geometry A
b
= va (Sec. 3.4.2.1).
Any influence on grain boundary mobility will be reflected in a change of
H
m
, V
∗
, and/or m
0
(resp. A
0
). Therefore, in the following we will discuss
the dependence of these kinetic parameters on the structure and chemistry of
grain boundaries.
© 2010 by Taylor and Francis Group, LLC
3.5 Experimental Results 223
0 10 20 30 40 50 60
0
1
2
3
4
5
g
r
o
w
t
h
r
a
t
e
[
m
m
/
m
i
n
]
ϕ
[deg]
0 102030405060
0
1
2
3
4
5
ϕ [deg]
growth rate [mm/min]
0 10 20 30 40 50 60
0
1
2
3
4
5
g
r
o
w
t
h
r
a
t
e
[
m
m
/
m
i
n
]
ϕ
[deg]
0 102030405060
0
1
2
3
4
5
ϕ [deg]
growth rate [mm/min]
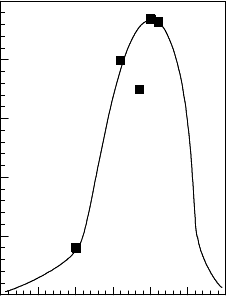
FIGURE 3.50
Change of boundary migration rate with orientation difference about a com-
mon 111 axis in Al [264].
3.5.3 Misorientation Dependence of Grain Boundary
Mobility
The long-known observation that pronounced crystallographic textures de-
velop during annealing of deformed metals was the first indication that grain
boundary mobility may depend on misorientation. Correspondingly, the first
findings on the orientation dependence of grain boundary velocity were ob-
tained in recrystallization experiments (Fig. 3.50) [264, 265, 269]. Such depen-
dencies were confirmed subsequently with experiments on bicrystals, which
do not only permit us to investigate all orientation relationships, but also to
determine the influence of various factors on grain boundary mobility, e.g.
temperature, pressure, nature and content of impurities etc. However, in the
majority of investigations grain boundary migration was considered for a very
few specific boundaries and provides only an incomplete characteristic of the
migration capability of grain boundaries [230]-[235], [270]-[272]. The misori-
entation dependence was studied extensively for lead, aluminum and zinc.
The misorientation dependence of the velocity of single boundaries in zone
refined lead was studied under a constant driving force (striation/subgrain/
structure, experimental technique N1, Table 3.3) and in a range of tempera-
tures [182] (Fig. 3.51). Well-pronounced extrema (maxima of grain boundary
velocity, minima of activation energy and preexponential factor, respectively)
could be associated with low Σ coincidence boundaries.
In aluminum the misorientation dependency of grain boundary mobility
© 2010 by Taylor and Francis Group, LLC
