Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

204 3 Grain Boundary Motion

y(x)

FIGURE 3.34

Illustration of the geometry and the surface tensions in the quarter-loop tech-

nique.

account that the right-hand end of the boundary moves freely along the line

x = b, the equilibrium condition for this end can be found from



−

∂W

∂y

x=b

= 0 (3.126)

From Eqs. (3.125) and (3.126) the equilibrium condition can be derived

γy



1+(y



)

− Δγ

x=b

= 0 (3.127)

or, expressing y



as a function of the contact angle

Θ,

γ cos

Θ=Δγ

(3.128)

Eq. (3.128) can be utilized to determine the relative grain boundary surface

tension γ and to estimate the free surface tension [259].

The actual form of the solution depends on how the surface tension and the

mobility vary from point to point at the boundary [256]. In case of impurity

drag some parts of the boundary may move freely, while the more slowly

3.4 Measurement of Grain Boundary Mobility 205

moving section is loaded with impurities. If the boundary mobility depends

only on temperature T and velocity v

= m

+(m

− m

) H (v − v

∗

) (3.129)

where H(ξ) is the Heavyside step function, deﬁned by

H(ξ)=



0,ξ<0

1,ξ>0

(3.130)

and m

are the mobilities of an impurity-free and an impurity-loaded

boundary, respectively; v

∗

is the critical value of the boundary velocity, where

the impurities can still move together with the boundary [193]. Because it is

evident that the surface tension varies from point to point much more slowly

than the mobility, it can be assumed [243] that γ =const.

The vertex of the half-loop moves fastest, and its velocity is equal to the

velocity V of the half-loop as a whole. If V<v

∗

, the boundary remains

attached to its impurities at any point, and its mobility is m = m

=const.

Integration of Eq. (3.122) then yields [243]

y = y

arc cos



−

(x−x



(3.131)

where y

and x

are the constants of integration. With the boundary condi-

tions (Eq. (3.123)), we obtain

V =

πγm

2γ

· m

(3.132)

y =

arc cos



−πx/a



(3.133)

The term 2γ/a can be referred to as the average driving force, and the quantity

πm

/2 then corresponds to the average half-loop mobility.

A half-loop, the velocity v of which exceeds v

∗

, consists of a boundary

segment which became detached (free) from impurities as well as a loaded

segment moving together with the impurities. The part of the boundary far

from the half-loop vertex moves relatively slowly and, therefore, does not

become detached from the impurities. The shape of the latter segment is

given by an expression similar to Eq. (3.131)

= y

+ b

arc cos



−

x−x



(3.134)

where b

= m

γ/V .

If V>v

∗

, the boundary at the vertex becomes detached from the impuri-

ties, and its shape is then

= y

+ b

arc cos



−

x−x



(3.135)

206 3 Grain Boundary Motion

where b

= m

γ/V .

At the point x

∗

on the boundary, which moves exactly with the velocity v

∗

)=y

∗

)



∗

)=y



∗

) (3.136)

The boundary cannot be discontinuous or contain kinks, since at a kink the

curvature of the boundary and, consequently, the driving force would become

inﬁnite.

The conditions (3.123) now change to

(0) = 0

(∞)=

(3.137)



(0) = ∞

and the integration constants y

, y

, x

,andx

are completely deﬁned

y(x)=

⎧

⎪

⎨

⎪

⎩

arc cos



−



, 0 ≤ x ≤ x

∗

− b

arc sin



−

x−x

∗

(

1−b

)



∗

<x<∞

⎫

⎪

⎬

⎪

⎭

(3.138)

where

∗

= −

∗

(3.139)

and the half-loop velocity is given by

∗

= V sin



− V



(3.140)

where V

= πγm

/a and V

= πγm

/a.

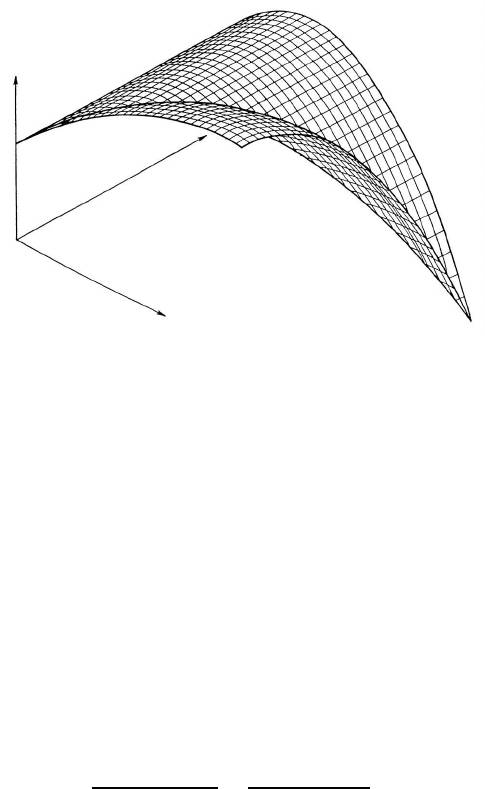
The change of shape of a half-loop on detachment from its impurities is

shown schematically in Fig. 3.35. The detachment from the impurities ﬂattens

the grain boundary. This eﬀect does not only apply to impurity atoms but also

to mobile particles. It follows from Eq. (3.140) that the detachment of a grain

boundary half-loop, more generally of a curved boundary, from its impurities

is more complicated than for a planar boundary. The dependence (3.140) is

plotted in Fig. 3.36. The various curves correspond to diﬀerent values of the

ratio α = V

. The diagram reﬂects the behavior of a grain boundary

half-loop at diﬀerent values of v

∗

but for a constant V

.Ifv

∗

large, the boundary moves together with its impurities, and its velocity is

(line a − b in Fig. 3.36). If v

∗

decreases and reaches the value V

(point b), some impurities become detached from the half-loop vertex, and

the boundary segment abruptly assumes the velocity corresponding to point c

(Fig. 3.36). Furthermore, as v

∗

decreases, more and more impurity atoms

become detached from the boundary, i.e. increasingly larger segments of the

3.4 Measurement of Grain Boundary Mobility 207

I II IIII II III

FIGURE 3.35

Changes in the shape of a half-loop boundary in the course of its detachment

from impurities: (I) before detachment; (II, III) diﬀerent stages of detachment.

boundary move freely, and the half-loop velocity approaches V

. In turn, if the

value v

∗

is increased again, the half-loop velocity follows the same curve

to point d in Fig. 3.36, and then discontinuously changes to V

(impurity

attachment).

The following transformation is very useful for the interpretation of the

calculations. It is clear from Eq.(3.121) that



v/V

1 − v

(3.141)

Substituting (3.136) into (3.117) and integrating with respect to ξ = v/V

V =

2γ



(ξV )dξ

1 − ξ

≡

2γ

M(V ) (3.142)

where 2γ/a is the average driving force acting on the half-loop; V is the

velocity of the half-loop as a whole; M(V ) is the average mobility of the

half-loop. If V<v

∗

and m(V )=m

= const., we ﬁnd M = πm

/2in

full agreement with the above analysis. Eq. (3.142) allows us to determine

the steady-state half-loop velocity as a function of the driving force, if we

know the dependence m(v), which determines the microscopic mobility of a

segment of the boundary with regard to its normal displacement. However,

experimental investigations usually give the macroscopic velocity of a half-

loop, and we come up against the inverse problem: knowing the dependence

of V on the driving force on the half-loop of width a, we have to ﬁnd the

dependence m(v). With this in mind, we will represent Eq. (3.142) in the

form

a(V )V

2γ



(v)dv

√

− v

≡



(v)





√

− v

(3.143)

208 3 Grain Boundary Motion

α = 0.1

α = 0.5

α = 0.7

α = 0.3

0.80.2 0.60.4

V/V

0.8

0.6

0.4

0.2

v*/V

α = 0.1

α = 0.5

α = 0.7

α = 0.3

0.80.2 0.60.4

V/V

0.8

0.6

0.4

0.2

v*/V

0.8

0.6

0.4

0.2

v*/V

FIGURE 3.36

Diagram used to determine the velocity of steady-state motion of a half-loop

(see text).

where a(V ) is the inverse function of V (a). This integral equation can be

solved with regard to m

(v)

(v)=

πγv



da(V )

V +2a(V )

√

− V

dV (3.144)

This establishes the full relationship between the microscopic kinetic proper-

ties of a grain boundary and the macroscopic properties of a half-loop.

The macroscopic approach provides a way for a pictorial interpretation of

the solution of the problem in the L¨ucke-Detert approximation. The average

mobility of a half-loop given by Eq. (3.142) can be easily deduced

M(V )=



πm

,V <v

∗

arc sin

∗

+ m

arc cos

∗

,V >v

∗



(3.145)

and the substitution of Eq. (3.145) into Eq. (3.142) yields Eq. (3.140). It is

obvious that the relation (3.142) corresponds to the extremum of the function

ψ(V )=



2γV − a



VdV

M(V )



(3.146)

since (3.146) is obtained by integrating (3.142) in the form 2γ−aV/M(V )=0.

It is easily seen that only the maxima of this function correspond to stable

3.4 Measurement of Grain Boundary Mobility 209

ψ/

FIGURE 3.37

Generalized dissipative function (see text).

steady-state motion. The velocities conforming to the minima of Ψ(V )de-

crease with increasing driving force, which is physically incorrect, and the

solutions are totally unstable. The function Ψ(V ) for diﬀerent values of v

∗

in the L¨ucke-Detert approximation is plotted in Fig. 3.37. Finally, it is noted

that for a linear dependency of the velocity on the driving force (M =const.)

the function Ψ is equivalent to the rate of dissipation (loss) of the free energy

of the system, which is related to the Onsager principle in the thermodynam-

ics of irreversible processes [260].

The grain boundary half- (and quarter-) loop are the only known experi-

mental techniques at present, where the grain boundary moves steadily. For

the reversed-capillary technique (N4, Table3.3) additional assumptions are

needed to solve the equation for the shape of a moving boundary [229, 242]

ρ(Ψ,t)dρ(Ψ,t)

(ϕ)γ∂β(Ψ)

∂Ψ

(3.147)

where ρ(Ψ,t) is the radius-vector of a point on the grain boundary in polar

coordinates; β(Ψ) is the angle between the tangent vector dρ to the grain

boundary at this point and the vector ρ(Ψ=0,t); m

(ϕ), γ(ϕ)arethemo-

bility and surface tension of the grain boundary, respectively; ϕ is the angle

of misorientation of the grain boundary (Fig. 3.38). If m

(ϕ)andγ(ϕ)are

independent of time, the space and time variables can be separated. In this

case the shape of the grain boundary does not change during motion, in other

words, the scaling condition is satisﬁed.

A general calculation of the grain boundary shape for the reversed-capillary

technique is diﬃcult and will not be presented here. In this respect a thermo-

dynamic concept [261] proved to be very beneﬁcial. Assuming as the physical

210 3 Grain Boundary Motion

(a)

(c)

IIII II

11’

450’

281.5’

161.5’

70’

32’

(b)

(a)

(c)

IIII II

11’

450’

281.5’

161.5’

70’

32’

(b)

FIGURE 3.38

Grain boundary displacement for reversed-capillary technique. (a) Boundary

geometry. (b) Calculated successive positions of a moving grain boundary in

a bicrystal. Numbers indicate annealing time in minutes (A

=10

−3

/s;

B =10

−2

m/s; γδ =5· 10

−5

J/m; Δγ

=10

−5

;Δγ

δ =10

−5

J/m; tan

α =0.275). (c) Traces of grain boundary motion in a Zn bicrystal (x400).

condition that an intermediate equilibrium of the boundary is always attained,

the free energy of the system at each instant is at a — relative — minimum,

despite the fact that irreversible processes occur in the system. One of the

merits of such an approach is that it is possible to determine the transition

process parameters. In this approach the problem can be reduced to deter-

mining a conditional extremum (minimum) of the free energy of the system.

The corresponding equations of motion are the coupling equations for this free

energy functional. It is ﬁnally noted that such concept is close to the Onsager

principle and to the principle of maximum rate of change of the thermody-

namic potential of the system [260]. In this approach [261] the shape of a grain

boundary moving under the action of its own curvature or other driving forces

can be determined (Fig. 3.25b,c). The reader is referred to [261] for details.

There are important reasons why we consider the problem of the shape of a

moving grain boundary so comprehensively. First, the description given above

is based on a visual concept, where all changes associated with the joint mo-

tion of grain boundary and impurity cloud, the detachment from the impurity

cloud, and the motion of the free grain boundary are clearly deﬁned in the

shape of the moving boundary. Second, up to now the grain structure of a

polycrystal is characterized by only one parameter — the mean grain size —

in spite of the fact that practically all grain boundaries are curved. Further,

we think that the given considerations are important and necessary because

of the discrepancy that all theories of grain boundary motion assume planar

grain boundaries, while real grain boundaries are curved, i.e. the theories are

applied without any corrections to grain boundary motion in polycrystals.

The analysis of the shape of the moving boundaries will become increasingly

interesting for computer simulations of grain growth and recrystallization.

Despite its importance, there has been only little research dedicated to the

shape of moving grain boundaries. A satisfactory agreement between exper-

3.4 Measurement of Grain Boundary Mobility 211

iment and theory was found when the shape of a grain boundary, moving

under the conditions of the reversed-capillary technique, was compared to the

theoretical shape approximated by a circular arc [236]. A recent investigation

[244] was conducted to compare the experimentally observed shape in the

quarter-loop technique with the corresponding calculations in the framework

of the L¨ucke-Detert approximation to analyze the principal question whether

boundary motion in the quarter-loop technique complies with scaling condi-

tions, and, in particular, to estimate the inﬂuence of the impurity atoms on

the shape of a moving grain boundary.

The quarter-loop technique was chosen since, on the one hand, considerable

detailed experimental research has been conducted about the eﬀect of grain

boundary mobility using this method, and on the other hand, it can be easily

treated theoretically [243]. Contrary to the “half-loop” situation, in this case

the grain boundary steady-state motion is a motion together with a triple

junction which is formed by three surfaces (the grain boundary and two free

surfaces) and, naturally, by the three corresponding surface tensions γ, γ

T 1

and γ

T 2

(Fig. 3.34). Equilibrium in that triple junction can be conserved if

there is no mass transfer (diﬀusion etc.) to change the shape of the triple

junction in this point. The problem can be considered under the assumption

of uniform grain boundary properties and quasi-two-dimensionality [244] by

using Eqs. (3.120)–(3.124). Eq. (3.148) describes the shape of a freely mov-

ing quarter-loop, i.e. which does not interact with impurity atoms and other

obstacles.

y(x)=ξ arc cos



−x/ξ+c



+ c

ξ =

2Θ

; c

=ln(sinΘ); c

= ξ



− Θ



(3.148)

The solution for a quarter-loop inﬂuenced by impurity drag can be derived

by the procedure extensively considered above (Eqs. (3.134)–(3.140)) except

that boundary condition (3.137) must be replaced by (3.124).

y(x)=

⎧

⎪

⎨

⎪

⎩

−(b

− b

)arc cos



sin Θ

∗



− b

+ b

arc cos



ln(sinΘ)−x



0 ≤ x ≤ x

∗

− b

+ b

arc cos

⎛

⎝

ln(sinΘ)−x

∗

„

−1

−x

⎞

⎠

x ≥ x

∗

(3.149)

where b

is:



arc cos



sinΘ

∗



+Θ−



−

arc cos



sinΘ

∗



−

(3.150)

The parameters in the function (3.149) are the width of the shrinking grain

a/2, the angle Θ of the grain boundary with the free surfaces in the triple junc-

212 3 Grain Boundary Motion

"loaded" segment

"free" segment

"loaded" segment

"free" segment

670

660

650

680

725 745 765 785 805 825

670

660

650

680

725 745 765 785 805 825

“free” segment

“loaded” segment

“free” segment

“loaded” segment

x [µm]

y(x) [µm]

(a)

(b)

(a)

(b)

"loaded" segment

"free" segment

"loaded" segment

"free" segment

670

660

650

680

725 745 765 785 805 825

670

660

650

680

725 745 765 785 805 825

“free” segment

“loaded” segment

“free” segment

“loaded” segment

x [µm]

y(x) [µm]

(a)

(b)

(a)

(b)

FIGURE 3.39

Intersection of “free” and “loaded” segment of the calculated grain boundary

shape (a) m

=0.0292, (b) m

=0.00245 (x

∗

- dashed line).

tion, the critical point x

∗

,andb

. The ﬁrst two parameters can be measured

directly in the experiment. The latter two have to be chosen in an appropriate

way to ﬁt the experimentally derived grain boundary shape. As can be seen

from Eqs.(3.134) and (3.135), b

= m

.Thepointx

∗

is the point of

intersection of the “free” and “loaded” segments of the grain boundary.

The value m

is a measure for how drastic the change between the

“free” and the “loaded” part in the point of intersection will be. Even if there

is no kink or discontinuity in the calculated grain boundary shape at point

∗

the change from the “free” to the “loaded” part will be more and more

abrupt for smaller and smaller values of m

(Fig. 3.39).

Corresponding experiments were carried out on aluminum bicrystals with

a 40.5

◦

111 tilt boundary. The samples diﬀered by the amount of dissolved

impurities. Bicrystals with a total impurity content of 0.4 ppm, 1.0 ppm,

3.4 Measurement of Grain Boundary Mobility 213

0 1 2 3 4 5 6 7 8

content of impurity [ppm]

-10

-09

-08

-07

[

]

0123 54678

c [ppm]

/s]

-9

-10

-8

-7

FIGURE 3.40

Dependence of the reduced grain boundary mobility on impurity content in

high purity Al.

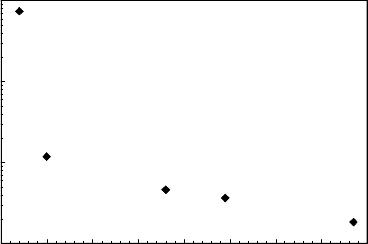
3.6 ppm, 4.9 ppm and 7.7 ppm were studied. The grain boundary mobil-

ity was extracted from in situ experiments of grain boundary motion (see

Sec. 3.4.2). After the measurement of grain boundary mobility the samples

were rapidly cooled to room temperature, and the grain boundary shape was

recorded with an image analysis system. The accuracy of locating the grain

boundary was about 15μm. The used mobility data [244] are given in Fig.

3.40.

A major change in the mobility was observed in the regime between 0.4 ppm

and 1.0 ppm, where the mobility drops drastically with increasing impurity

content. This may be due to the attachment of impurities to the grain bound-

ary [244]. In the specimen with 0.4 ppm solute atoms the grain boundary had

a mobility of 7.4 ·10

−8

/s which can be assumed to be the mobility m

the “free” moving grain boundary. In this context “free” means that there are

no additionally adsorbed atoms at the grain boundary, i.e. the concentration

of the solute atoms in the grain boundary does not diﬀer from the concentra-

tion of the solute atoms in the bulk. At larger impurity content the mobility is

no longer determined by the intrinsic grain boundary mobility, but rather by

the mobility m

of the impurities. The investigation proves that the inﬂuence

of the impurity atoms on grain boundary properties and behavior is rather

strong even in very pure materials. The experimentally measured shape of a

moving grain boundary (Al with 1.0 ppm impurities) and the shape, calcu-

lated according to Eq. (3.148), which does not take into consideration impurity

drag, are compared in Fig. 3.41. The large discrepancy is obviously and ap-

parently due to the neglect of boundary-impurity interactions. However, with

and m

determined as explained above, the measured boundary shape