Горячкин А.Е. От механической физики к живой природе
Подождите немного. Документ загружается.

90
означает, что в силу существования принципа подобия при-
родных процессов и распространения различных видов энер-
гии любое природное явление может быть описано одними
и теми же соотношениями. Надо просто использовать пара-
метры, соответствующие конкретному типу взаимодействия.
Просто помните, что любое природное взаимодействие про-
исходит в собственных пространственно-временных рамках и
должно учитывать только те параметры, которые только ему
и присущи. При помощи такого подхода так же легко можно
описать взаимодействия тел друг с другом. Как мы помним,
это всегда происходит через свойства взаимодействующих
тел. Главное – разобраться в задействованных в конкретном
случае свойствах.
91

92
ГЛАВА III
СИСТЕМА ИЗМЕРЕНИЙ
ГЛАВНОЕ СОКРОВИЩЕ
ДИНАМИЧНОЙ ГЕОМЕТРИИ
Немецкий математик, астроном, геометр и оптик, работавший
на границе шестнадцатого и семнадцатого веков, вошел в науч-
ную историю как настоящий романтик. Именно Кеплер расшиф-
ровал симметрию снежинок и доказал, что двух одинаковых не
существует
45
. Он подарил нам с вами «среднее арифметическое»,
побочным эффектом которого стала статистика. Кеплер заложил
первые камни в фундамент современного математического ана-
лиза и новейшей астрономии. Именно этот скромный немецкий
ученый несколько столетий назад доказал известный сегодня лю-
бому продавцу факт, что наибольшая плотность упаковки шаров
достигается при пирамидальном построении. Правда, доказал он
это эмпирически, а математически задачу сумели доказать лишь
в 1998 году. Кстати, Кеплер также подарил физикам уже извест-
ные нам термины «инерция» и «гравитационное притяжение». А
еще за целых сто лет до Ньютона немец выдвинул предположение,
что приливы и отливы Мирового океана сильно зависят от лунного
цикла, а планеты должны взаимно притягиваться. В своей книге
«Новая астрономия» он писал: «В природе существует взаимное,
телесное стремление сходных или родственных тел к единству и
соединению. Источником этой силы являются магнетизм и враще-
45
Об этом сейчас знает любой ребенок.

93
ние Солнца и планет вокруг своей оси». Думаю, с вершины уже
полученных нами знаний вы легко оцените всю прелесть мысли
средневекового ученого.
Так вот этот во всех отношениях приятный мужчина как-то раз
сказал: «Геометрия владеет двумя сокровищами: одно из них – те-
орема Пифагора
46
, другое – деление отрезка в среднем и крайнем
отношении». Под последним он подразумевал некую пропорцию,
магию, которой он так и не смог постичь. Впрочем, не только он,
а даже Эйнштейн, который долгие годы бился над высшим пред-
назначением симметрии, именуемой сегодня «золотым сечением».
Основная магия этого сечения состоит в том, что оно не имеет ни-
чего общего с наукой в общепринятом понимании самого словосо-
четания. Золотое сечение, как доказали многочисленные исследо-
вания, явление психологическое и может встречаться в самых уди-
вительных областях: в природе, в биологии, на валютном рынке, на
прогулке, в магазине, в фотографии, в изобразительном искусстве
и даже религии. Может быть, именно поэтому в древнем Египте
знания о «Золотом сечении» были доступны только фараонам и
ближайшей свите, а христиане в средние века спасались от дьявола
и нечистой силы при помощи не только чеснока, но и пентаграмм
«золотого сечения». Чего уж таить, сам Пифагор вел кружок для
ограниченного круга слушателей, в котором обсуждалась и изуча-
лась мистика «золотого сечения».
Кстати, даже если вы еще ни разу не слышали словосочетания
«золотое сечение», вы наверняка сталкивались с рисунком, которо-
му частенько незаслуженно приписывают начало дискуссии. Это
«Человек» Леонардо Да Винчи
Это, разумеется, не совсем так. Ведь даже сам термин появил-
ся в 1835 году, и ввел его в обиход Мартин Ом, немецкий физик и
математик, брат Георга Ома, который объяснил всем, какова связь
между напряжением, силой тока и сопротивлением проводника в
электрической цепи
47
.
Надо сказать, что от подобного подобострастного отношения к
«золотому сечению» мир не избавился до сих пор. Спросите, у лю-
46
Она гласит, что в прямоугольном треугольнике площадь квадрата, построенного на
гипотенузе, равна сумме площадей квадратов, построенных на катетах. Если нарисовать,
получатся те самые Пифагоровы штаны.
47
U=RI, I=U/R

94
95
бого ученого, что это такое, и он ответит вам, что это и научный фе-
номен, и этический принцип. Кроме того, это еще и закон красоты,
божественное сочетание и мистическая тайна, которую мы с вами
попытаемся немного прояснить.
ЗОЛОТОЕ СЕЧЕНИЕ
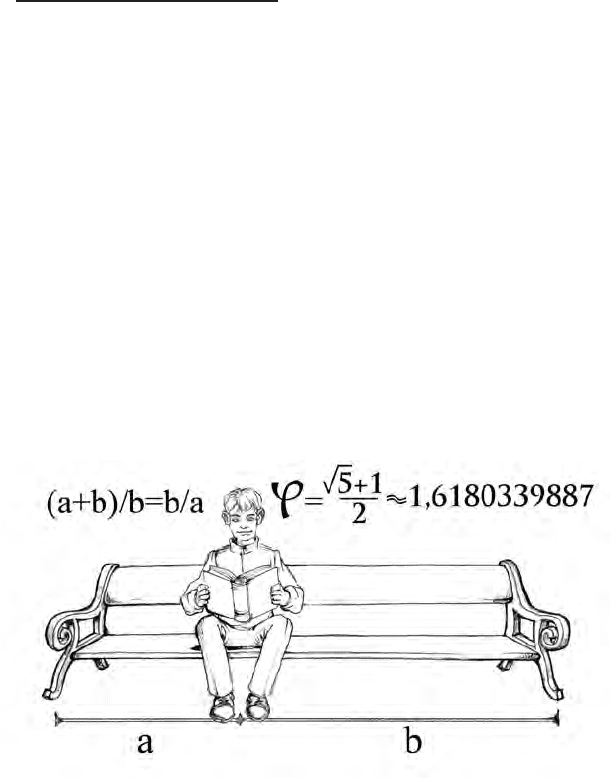
Освежите в памяти банальную ситуацию, которую вы прожи-
вали не один раз, сядьте мысленно на пустую скамейку. А еще
лучше – проделайте это по-настоящему, эксперимента ради. Смею
предсказать, что с максимальной вероятностью вы сядете на нее не
ровно посередине, не с самого края, а так, что одно отношение ча-
сти скамейки к другой относительно вашего тела будет примерно
1,62. Все. Вы сами абсолютно инстинктивно сотворили «золотое
сечение». Казалось бы, какая в этом мистика, если так называемую
божественную пропорцию так легко создать. Давайте разбираться
более детально.
Научными словами, ваш плюх на скамейку или диван описы-
вается следующим образом: «золотая пропорция – деление непре-
рывной величины на две части в таком соотношении, при котором
меньшая часть так относится к большей, как большая ко всей вели-
чине». Не знаю как вам, а мне ближе всего картинки:
Собственно, длина изначальной величины никакой роли не
играет. Подставьте любое значение в формулу пропорции, и после

96
нескольких преобразований вы получите следующее алгебраиче-
ское выражение «золотого сечения»:
Хочу сказать, что знак приблизительности и многоточие в кон-
це – отнюдь не дань мистической ауре божественной пропорции.
Точное математическое выражение так никто вычислить и не смог.
Даже Альберт Эйнштейн. Однако здесь мы наглядно, в числах, ви-
дим, что золотая пропорция приближена к числу 1.62, тому самому
коэффициенту, на который мы с вами поделили скамейку/диван/
качели, когда сели на них. Отсюда возникает первый вопрос: как
же так получилось, что мы, не читая учебника и безо всяких специ-
альных знаний, где-то на уровне подсознания чувствуем «золотую
пропорцию»?
Человек различает весь окружающий его мир по форме, раз-
умеется, если речь идет о визуальном восприятии. Те или иные
предметы нам всегда заведомо кажутся более привлекательны-
ми. Причем почти у ста процентов людей вне зависимости от
расы, пола, национальности и возраста эта тяга совпадает
48
. При
детальном изучении понравившихся предметов ученые замети-
ли, что все они созданы вокруг «золотого сечения». Например,
лепестки цветов соотносятся друг с другом по этому самому
принципу. Или же вы замечали, что лицо у вас несимметричное,
а левая и правая части немного разнятся. Это тоже «золотая сим-
метрия». Точнее, полное отсутствие идеальной симметрии, что
и делает наши лица столь притягательными для других. Легкая
неравность делает для людей предметы более гармоничными и,
по крайней мере визуально, более совершенными в функцио-
нальном смысле.
У вас наверняка бывало так, что рисуете вы ребенка, а полу-
чается взрослый. Рисуете женщину – получается мужчина, хоть и
немного женоподобный. И наоборот. Рисуете взрослого – выходит
ребенок, рисуете женщину – получается мужчина. Если вы сами
этого не видите, так как полностью поглощены работой, то вам,
48
Ради чистоты эксперимента ученые, проводившие исследования, отбросили те предметы,
которые нас притягивают из-за их необходимости. Например, таблетки, когда мы болеем.
97
возможно, об этом могли намекнуть другие. В чем дело? Все в тех
же пропорциях. Дело в том, что части нашего тела также построе-
ны вокруг «золотой пропорции». Ученые считали, пересчитывали,
а немецкий художник Альбрехт Дюрер закрепил, чем положил на-
чало академической школе изобразительного искусства: соотноше-
ние частей человеческого тела на разных этапах жизни отличается,
но крутится вокруг значения 1.62. Речь идет в первую очередь о
соотношении длины плеча, предплечья и кисти, кисти и пальцев,
голени и ступни. Итак, запоминайте, чтобы потом блеснуть: у но-
ворожденного пропорция выражается как 1:1. К 13 годам она равна
1.6, а к 21 году достигает значения 1.625. По половому признаку
пропорции делятся следующим образом: у мужчин она равняется
– 1.62, у взрослой женщины – 1.61.
Описанное выше пропорциональное соотношение можно уви-
деть в греческих статуях, египетских саркофагах и украшениях, а
также многочисленных работах художников. На заре XX века те-
ории о «золотом сечении» значительно формализовали и сегодня
активно используют в новейших отраслях: технике, графическом
дизайне, создании одежды и предметов интерьера.
Впрочем, если у вас нет сил проверять «на золото мебель» в
вашем доме или измерять самого себя, есть и более легкий способ
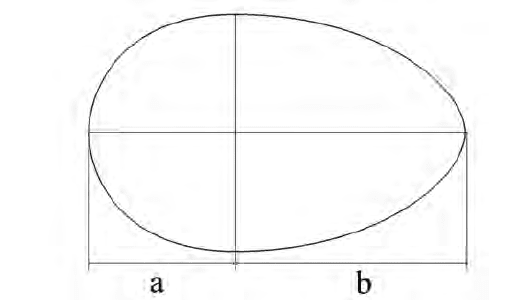
рассмотреть принцип золотого сечения. Возьмите простое кури-
ное яйцо.
Оно кажется вам привычным, а между прочим, его красоту и
прелесть строения воспел сам Гете.
Или же ящерица. Она кажется нам приятной и дружелюбной не-
спроста: длина ее хвоста относится к длине остального тела как
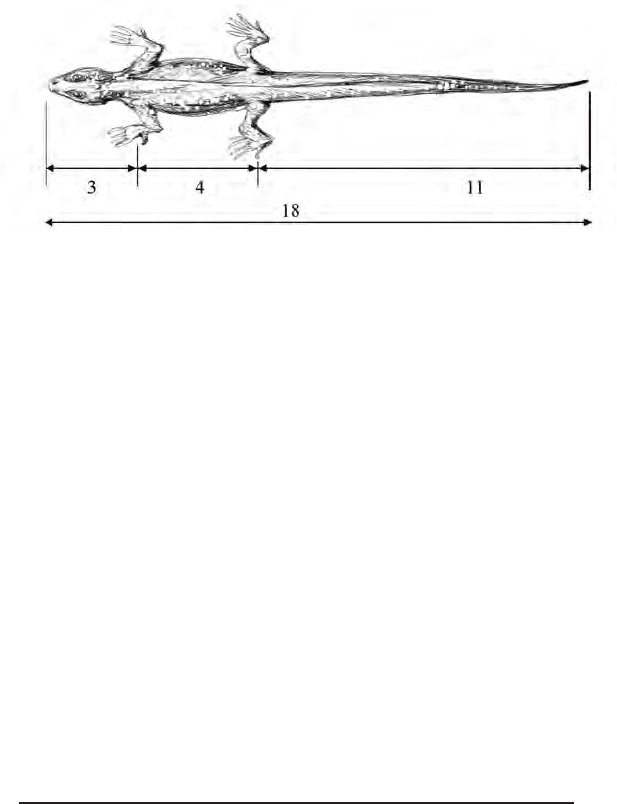
98
62 к 38, что равняется примерно 1.63. Это не идеальная пропорция
золотого сечения, но максимально приближенная.
Саламандра – другое название ящерицы – великолепный при-
мер проявления золотых пропорций и божественной симметрии
относительно роста и движения.
Обнаружить примеры «золотой пропорции» можно и под микро-
скопом: спираль ДНК, гены, молекулы, строение головного мозга
и наших органов – все построено по принципу золотого сечения.
Если изобразить время в виде геометрического графика, то ста-
новится понятно, что наша жизнь также развивается по принципу
золотого сечения. Впрочем, биоритмы, тембр голоса, частота дыха-
ния и эмоции также эволюционируют по принципу золотого сече-
ния. Именно поэтому мы практически безошибочно делим скамей-
ку по данному принципу. Именно поэтому мы можем разглядеть
прекрасное в, казалось бы, абсолютно не идеальном и, наоборот, с
легкой душой отказаться от идеала в пользу немного кривого. Моя
фраза звучит как «эволюционирует», то есть «развивается». Ведь
«золотое сечение» – не антоним идеальной симметрии. Оно и есть
динамическая симметрия, не терпящая только одного – измерения
жестким метром.
ЛЕОНАРДО ПИЗАНСКИЙ И ЕГО КРОЛИКИ
Леонардо Пизанский – один из тех выдающихся ученых, о кото-
рых удивительным образом почти никому ничего не известно. За
свою долгую жизнь – итальянец прожил больше 80 лет – он сумел
совершить свыше десяти путешествий по странам Азии, поуча-

99
ствовать в кровавых баталиях и написать массу трактатов о мате-
матике, которые, к великому сожалению, так и не получили ши-
рокой известности. Главной причиной такого провала стала сама
эпоха, омраченная Крестовыми походами.
Леонардо Пизанский, изредка именуемый Фибоначчи
49
, ро-
дился около 1170 года в городе Пиза в семье местных вельмож.
Как и все отпрыски богатеев того времени, маленький Леонардо
получил хорошее домашнее образование, круглую сумму на пу-
тешествия и благословение отца на дальние странствия. С таким
нехитрым багажом будущий ученый отправился на Восток, на
территорию современного Узбекистана, Индии, Сирии, Алжира
и Сицилии (ошибки здесь нет – раньше Италия не считала себя
одной страной, и люди из соседних регионов даже не понимали
наречий друг друга). Выбор Леонардо не был удивительным для
того времени. Дело в том, что арабский мир в тот момент был
на высоте – ученые, товары, предприниматели, великолепные
войны и другие прелести средневековой цивилизации так или
иначе были неразрывно связаны с мусульманским Востоком.
Естественно, такие странствия сулили молодому человеку массу
впечатлений. Однако нас его странствия интересуют лишь с сугу-
бо научной точки зрения. Например, из первого путешествия он
привез в Европу и распространил арабские цифры, которыми мы
пользуемся по сей день.
А в 1202 году Фибоначчи выпустил книгу с лаконичным названи-
ем «Книга о счетной доске». Это был своеобразный сборник самых
интересных на тот момент математических задачек. Самого его, как
и положено купеческому сыну, интересовала связанная с торговлей:
сколько пар кроликов у одной пары родится? Итогом его кропотли-
вой работы и долгих размышлений стала вот такая вот таблица:
Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 И т.д.
Пары
кроликов
0 1 1 2 3 5 8 13 21 34 55 89 144 И т.д.
49
В переводе с итальянского означает либо «сын благонамеренного человека», либо «хоро-
ший сын родился»
