Голованов М.И. Нестандартные логики. Реляционная семантика
Подождите немного. Документ загружается.


14 Лекция 15. Алгебра Линденбаума
Пусть Λ некоторое расширение логики Lp, формулы которого построены только с по-
мощью связок ∧, ∨, →, и P - некоторое множество пропозициональных переменных.
Рассмотрим множество формул F or
P
в языке логики Λ, построенных с использова-
нием только переменных из множества P .
Поскольку логика Λ содержит логику Lp, то все ранее доказанные в логике Lp
утверждения справедливы и в логике Λ, в частности, теорема дедукции и следующие
производные правила и эквивалентности формул.
p, q
p ∧ q
,
p → q, q → r
p → r
,
p → q
¬q → ¬p
,
p → q
(q → r ) → (p → r)
.
1a. p ∧ p ≡ p, 1b. p ∨ p ≡ p,
2a. (p ∧ q) ∧ r ≡ p ∧ (q ∧ r), 2b. (p ∨ q) ∨ r ≡ p ∨ (q ∨ r),
3a. p ∧ q ≡ q ∧ p, 3b. p ∨ q ≡ q ∨ p,
4a. p ∧ (p ∨ q) ≡ p, 4b. p ∨ (p ∧ q) ≡ p,
5a. p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r), 5b. p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r),
6. ((p ∨ q) → r) ≡ ((p → r) ∧ (q → r)),
7. p → (q ∧ r) ≡ (p → q) ∧ (p → r),
8. ((p → q) → q) → q ≡ p → q,
9. (p → q) ≡ [((p → q) → p) → q],
10. ¬¬¬p ≡ ¬p,
11. ¬(p ∨ q) ≡ ¬p ∧ ¬q
Справедливы также следующие свойства отношения ≡ формальной эквивалент-
ности формул:
1) α ≡ α,
2) если α ≡ β, то β ≡ α,
3) если α ≡ β и β ≡ γ, то α ≡ γ,
4) если α
1
≡ α
2
и β
1
≡ β
2
, то:
a) α
1
∧ β
1
≡ α
2
∧ β
2
,
b) α
1
∨ β
1
≡ α
2
∨ β
2
,
c) α
1
→ β
1
≡ α
2
→ β
2
.
Свойства 1)-3) были доказаны ранее. Докажем свойство 4). Для доказательства
воспользуемся теоремой о замене эквивалентных, которая также была доказана для
логики Lp.
Так как α
1
≡ α
2
, то в силу теоремы о замене эквивалентных α
1
∧ β
1
≡ α
2
∧ β
1
. В
силу второй эквивалентности β
1
≡ β
2
получаем α
2
∧ β
1
≡ α
2
∧ β
2
. В силу свойства 3)
α
1
∧ β
1
≡ α
2
∧ β
2
. Остальные эквивалентности доказываются аналогично.
Поскольку отношение ≡ рефлексивно, симметрично и транзитивно, то совокуп-
ность всех формул F or
P
в языке логики Λ разбивается данным отношением на по-
парно непересекающиеся классы эквивалентных формул. Рассмотрим фактормно-
жество F or
P
/≡, т.е. множество, элементами которого являются классы эквивалент-
ных формул. Обозначим класс эквивалентности, содержащий формулу ϕ, символом
[ϕ]. На построенном множестве определим операции ∧, ∨ и → следующим образом:
[ϕ] ∧ [ ψ] = [ϕ ∧ ψ], [ϕ] ∨ [ψ] = [ϕ ∨ ψ], [ϕ] → [ψ] = [ϕ → ψ]. В силу свойств a),
b) и c) из п. 4) операции определены корректно, т.е. результат операции, приме-
нённой к классам эквивалентности не зависит от выбора представителей в данных
классах, а полностью определяется выбором класса. Обозначим эту алгебру E
Λ
(P )
81
и будем называть её алгеброй Линденбаума логики Λ для формул, порождённых
переменными из множества P . Так как любой элемент имеет вид [ϕ(p
1
, . . . , p
n
)],
где p
1
, . . . , p
n
пропозициональные переменные из множества P , и по определению
[ϕ(p
1
, . . . , p
n
)] = ϕ([p
1
], . . . , [p
n
])], то множество классов эквивалентности {[p]|p ∈ P }
является множеством порождающих элементов алгебры E
Λ
(P ).
Теорема 14.1. Формула ϕ(p
1
, . . . , p
n
) принадлежит логике Λ тогда и только тогда,
когда её значение при любых значениях переменных p
1
, . . . , p
n
в алгебре E
Λ
равно
[p → p].
Доказательство. Класс [p → p] содержит все доказуемые формулы логики Λ. В
самом деле, последовательность ϕ, ϕ → (ψ → ϕ), ψ → ϕ является выводом формулы
ψ → ϕ из ϕ. Поэтому если ϕ доказуема, то и ψ → ϕ доказуема. Симметричным
образом: если ψ доказуема, то и ϕ → ψ доказуема, т.е. для любых доказуемых формул
ϕ и ψ справедливо утверждение ϕ ≡ ψ. В частности, ϕ ≡ p → p. Элемент [p → p]
далее будем обозначать >.
Пусть ϕ(p
1
, . . . , p
n
) доказуемая формула логики Λ . Тогда для любых формул
ψ
1
, . . . , ψ
n
формула ϕ(ψ
1
, . . . , ψ
n
) также доказуема. Следовательно [ϕ(ψ
1
, . . . , ψ
n
)] =
[p → p]. С другой стороны, в силу определения операций ϕ([ψ
1
], . . . , [ψ
n
]) = [ϕ(ψ
1
, . . . , ψ
n
)].
То есть значение доказуемой формулы при любых значениях входящих в неё пере-
менных всегда одно и то же и равно >.
Обратно, пусть при любых значениях переменных p
1
, . . . , p
n
значение формулы
ϕ(p
1
, . . . , p
n
) равно >. В частности ϕ([p
1
], . . . , [p
n
]) = >. Так как ϕ([p
1
], . . . , [p
n
]) =
[ϕ(p
1
, . . . , p
n
)], т.е. ϕ(p
1
, . . . , p
n
) ≡ p → p и формула ϕ(p
1
, . . . , p
n
) доказуема.
Теорема доказана. ¥
Если для любого конечного множества P пропозициональных переменных алгеб-
ра E
Λ
(P ) конечна, то логику Λ будем называть локально конечной.
Покажем, что классическая позитивная логика локально конечна. Пусть P =
{p
1
, . . . , p
n
}. Как было показано, любая формула классической позитивной логики
эквивалентна формуле нормального вида D
1
∧ · · · ∧ D
m
. Если конъюнктивный член
D
i
содержит подформулу вида p ∨ (p → q), p → p или (p → q) ∨ (q → r), то D
i
яв-
ляется доказуемой формулой. Для произвольной формулы ψ и доказуемой формулы
ϕ справедлива эквивалентность ψ ∧ ϕ ≡ ψ. Поэтому можно считать, что недоказу-
емая конъюнкция D
1
∧ · · · ∧ D
m
не содержит доказуемых конъюнктивных членов.
Кроме того в силу идемпотентности дизъюнкции и конъюнкции можно считать, что
все дизъюнктивные члены каждой из формул различны и все формулы D
i
также
различны. Из n переменных {p
1
, . . . , p
n
} можно составить n
2
различных имплика-
ций вида p
i
→ p
j
. Таким образом из переменных {p
1
, . . . , p
n
} можно составить 2
n
2
+n
различных формул вида D
i
. Всего формул нормального вида существует 2
2
n
2
+n
. По-
скольку часть этих формул будут доказуемыми, то в данном случае число элементов
алгебры E
Λ
(P ) при Λ = Lp
+
и P = {p
1
, . . . , p
n
} будет строго меньше 2
2
n
2
+n
. То есть
логика Lp
+
локально конечна.
Введём на элементах алгебры E
Λ
(P ) бинарное отношение 6, определив его сле-
дующим образом: [ϕ] 6 [ψ], если формула ϕ → ψ доказуема. Покажем, что данное
определение корректно, т.е. не зависит от выбора представителей в классах эквива-
лентности. Пусть ϕ ≡ ϕ
1
, ψ ≡ ψ
1
и формула ϕ → ψ доказуема. В силу определения
эквивалентности формула ϕ
1
→ ϕ доказуема. По правилу сечения доказуема и фор-
мула ϕ
1
→ ψ. Применяя правило сечения к формулам ϕ
1
→ ψ и ψ → ψ
1
приходим
к выводу, что формула ϕ
1
→ ψ
1
также доказуема. Итак [ϕ] 6 [ψ] при любом выборе
формул в классах [ϕ] и [ψ].
82
Лемма 14.2. Отношение 6 обладает следующими свойствами:
1) [ϕ] 6 [ϕ],
2) если [ϕ] 6 [ψ] и [ψ] 6 [ϕ], то [ϕ] = [ψ],
3) если [ϕ] 6 [ψ] и [ψ] 6 [θ], то [ϕ] 6 [θ],
4) если [ϕ] 6 [ψ], то [ϕ] ∧ [θ] 6 [ψ] ∧ [θ],
5) если [ϕ] 6 [ψ], то [ϕ] ∨ [θ] 6 [ψ] ∨ [θ],
6) если [ϕ] 6 [ψ], то [θ] → [ϕ] 6 [θ] → [ψ],
7) если [ϕ] 6 [ψ], то [ψ] → [θ] 6 [ϕ] → [θ].
Доказательство. Свойство 1) следует из утверждения ` ϕ → ϕ. Условия утвер-
ждения 2) означают ` ϕ → ψ и ` ψ → ϕ, т.е. ϕ ≡ ψ и [ϕ] = [ψ]. Условия свойства
3) означают ` ϕ → ψ и ` ψ → θ. Откуда по правилу сечения получаем ` ϕ → θ, т.е.
[ϕ] 6 [θ]. В силу условия [ϕ] 6 [ψ] формула ϕ → ψ доказуема.
1. ϕ ∧ θ гипотеза,
2. ϕ ∧ θ → ϕ аксиома A3,
3. ϕ из 1, 2 по m.p.,
4. ϕ → ψ доказуемая формула,
5. ψ из 3, 4 по m.p.,
6. ϕ ∧ θ → θ аксиома A4,
7. θ из 1, 6 по m.p.,
8. ψ ∧ θ из 5, 7 по правилу объединения посылок.
Мы показали, что ϕ ∧ θ ` ψ ∧ θ. Отсюда следует справедливость свойства 4).
Докажем свойство 5).
1. ϕ → ψ доказуемая формула,
2. ψ → ψ ∨ θ аксиома A6,
3. ϕ → ψ ∨ θ из 1, 2 по правилу сечения,
4. θ → ψ ∨ θ аксиома A7,
5. (ϕ → ψ ∨ θ) → ((θ → ψ ∨ θ) → (ϕ ∨ θ → ψ ∨ θ))
аксиома A8,
6. ((θ → ψ ∨ θ) → (ϕ ∨ θ → ψ ∨ θ)) из 3, 5 по m.p.,
7. (ϕ ∨ θ → ψ ∨ θ) из 4, 6 по m.p..
Следовательно формула (ϕ ∨ θ → ψ ∨ θ) также доказуема и свойство 5) справед-
ливо.
Свойства 6) и 7) означают, соответственно, что операция → монотонна по второму
аргументу, и антимонотонна по первому аргументу. Докажем свойство 6). Условие
[ϕ] 6 [ψ] означает, что формула ϕ → ψ доказуема. В этом случае последовательность
формул θ → ϕ, θ, ϕ, ϕ → ψ, ψ показывает справедливость утверждения θ → ϕ, θ ` ψ.
Применяя к последнему утверждению теорему дедукции, получим θ → ϕ ` θ →
ψ, что и означает справедливость свойства 6). Докажем свойство 7). По условию
доказываемого свойства формула ϕ → ψ доказуема. Последовательность формул
ϕ → ψ, ψ → θ, ϕ → θ является выводом по правилу сечения формулы ϕ → θ из
гипотезы ψ → θ, т.е. в силу теоремы дедукции (ψ → θ) → (ϕ → θ) и [ψ → θ] 6 [ϕ →
θ]. Лемма доказана. ¥
Итак множество F or
P
/≡ является частично упорядоченным множеством с отно-
шением 6. Докажем, что частично упорядоченное множество hF or
P
/≡, 6i является
решёткой. Напомним, что наибольшей нижней гранью подмножества M частично
упорядоченного множества является элемент a, удовлетворяющий условиям: 1) для
любого x ∈ M(a 6 x), 2) если для любого x ∈ M(c 6 x), то c 6 a. Двойственным об-
разом: наименьшей верхней гранью подмножества M частично упорядоченного мно-
83
жества является элемент b, удовлетворяющий условиям: 1) для любого x ∈ M(x 6 b),
2) если для любого x ∈ M(x 6 c), то b 6 c.
Лемма 14.3. Для любых двух элементов [ϕ] и [ψ] справедливы следующие утвер-
ждения:
а) [ϕ] ∧ [ψ] является наибольшей нижней гранью множества {[ϕ], [ψ]},
б) [ϕ] ∨ [ψ] является наименьшей верхней гранью множества {[ϕ], [ψ]},
в) [ϕ] → [ψ] является наибольшим решением неравенства [X] ∧ [ϕ] 6 [ψ].
Доказательство.
а) Неравенства [ϕ] ∧ [ψ] 6 [ϕ] и [ϕ] ∧ [ψ] 6 [ψ] вытекают непосредственно из аксиом
A3 и A4, и определения отношения порядка. Пусть [θ] 6 [ϕ] и [θ] 6 [ψ]. В силу
определения отношения порядка это означает ` θ → ϕ и ` θ → ψ. Формула (θ →
ϕ) → ((θ → ψ) → ( θ → ϕ ∧ ψ)) является аксиомой вида A8. Отсюда двукратным
применением правила modus ponens легко получаем ` θ → ϕ ∧ ψ, т.е. [θ] 6 [ϕ] ∧ [ψ].
б) Неравенства [ϕ] 6 [ϕ] ∨ [ψ] и [ψ] 6 [ϕ] ∨ [ψ] также вытекают непосредственно из
аксиом A6 и A7, и определения отношения порядка. Пусть [ϕ] 6 [θ] и [ψ] 6 [θ]. В
этом случае формулы ϕ → θ и ψ → θ доказуемы. Доказуемость формулы ϕ ∨ ψ → θ
вытекает из приведённых формул и аксиомы A8: (ϕ → θ) → ((ψ → θ) → (ϕ∨ψ → θ)).
Таким образом [ϕ] ∨ [ψ] 6 [θ], т.е. [ϕ] ∨ [ψ] наименьшая верхняя грань множества
{[ϕ], [ψ]}.
б) Покажем, что [ϕ] → [ψ] является решением неравенства [X] ∧ [ϕ] 6 [ψ]. Для этого
нужно показать, что формула ψ выводима из гипотезы (ϕ → ψ) ∧ ϕ.
1. (ϕ → ψ) ∧ ϕ гипотеза,
2. (ϕ → ψ) ∧ ϕ → ϕ аксиома A4,
3. ϕ из 1, 2 по правилу m.p.,
4. (ϕ → ψ) ∧ ϕ → (ϕ → ψ) аксиома A3,
5. ϕ → ψ из 1, 4 по правилу m.p.,
6. ψ из 3, 5 по правилу m.p..
Теперь покажем, что [ϕ] → [ψ] является наибольшим решением неравенства [X]∧
[ϕ] 6 [ψ ]. Пусть [θ] некоторое решение неравенства [X] ∧ [ϕ] 6 [ψ], т.е. формула
θ ∧ ϕ → ψ доказуема. В логике Lp формула θ ∧ ϕ → ψ эквивалентна формуле θ →
(ϕ → ψ). Следовательно формула θ → (ϕ → ψ) также доказуема, что означает в
соответствии с определением справедливость неравенства [θ] 6 ([ϕ] → [ψ]). Лемма
доказана. ¥
Логику Λ с логическими связками ∗
1
, . . . , ∗
n
будем называть алгебраической, ес-
ли существует алгебра A с операциями ∗
1
, . . . , ∗
n
и выделенным элементом > такая,
что ϕ(p
1
, . . . , p
n
) ∈ Λ тогда и только тогда, когда значение формулы ϕ(p
1
, . . . , p
n
)
при любых значениях переменных равно >. Мы показали, что любое расширение
логики Lp с логическими связками ∧, ∨, → является алгебраической логикой. Пока-
жем, что расширение логики Lj
¬
также является алгебраической логикой. Алгебра
Линденбаума в данном случае определяется так же как и для расширений логи-
ки Lp. Нам необходимо убедиться лишь в корректности определения операции ¬. В
логике Lj
¬
была доказана формула (p → q) → (¬q → ¬p). Если ϕ ≡ ψ, то фор-
мулы ϕ → ψ и ψ → ϕ доказуемы. Поскольку формулы (ϕ → ψ) → (¬ψ → ¬ϕ) и
ψ → ϕ) → (¬ϕ → ¬ψ) также доказуемы, то формулы ¬ψ → ¬ϕ и ¬ϕ → ¬ψ доказуе-
мы. Следовательно ¬ϕ ≡ ¬ψ и операция ¬[ϕ] не зависит от выбора представителя в
классе эквивалентности [ϕ]. Итак справедлива
Теорема 14.4. Любое расширение Λ логики Lj
¬
является алгебраической логикой.
84
Формула ϕ принадлежит логике Λ тогда и только тогда, когда её значение равно
> = [p → p] при любых значениях переменных в алгебре Линденбаума логики Λ.
Поскольку в логике Lj
¬
формула p → (¬p → q) эквивалентна формуле p∧¬p → q,
то справедлива
Лемма 14.5. В алгебре Линденбаума любой суперинтуиционистской логики эле-
мент [p ∧ ¬p] является наименьшим элементом этой алгебры.
Теорема 14.6. Любая нормальная модальная логика Λ является алгебраической.
Формула ϕ принадлежит логике Λ тогда и только тогда, когда её значение равно
> при любых значениях переменных в алгебре Линденбаума логики Λ.
Поскольку нормальная модальная логика содержит все доказуемые формулы
классического исчисления высказываний, то для доказательства данной теоремы до-
статочно доказать только корректность определения операции 2. Пусть формула
ϕ → ψ доказуема. Тогда формула 2(ϕ → ψ) также доказуема. Применяя к получен-
ной формуле и аксиоме 2(ϕ → ψ) → (2ϕ → 2ψ). Получим ` 2ϕ → 2ψ. Поскольку
эквивалентность ϕ ≡ ψ предполагает доказуемость формул ϕ → ψ и ψ → ϕ, то
получаем 2ϕ ≡ 2ψ. То есть операция 2 на классах эквивалентности определена
корректно.
Отметим, что в силу эквивалентностей, сформулированных в начале этой лекции,
операции ∧ и ∨ в алгебрах Линденбаума обладают свойствами идемпотентности,
ассоциативности, коммутативности и дистрибутивности, справедлив закон поглоще-
ния. Поскольку на этих алгебрах введено также отношение порядка, то необходимо
отметить, что эти алгебры являются дистрибутивными решётками с наибольшим
элементом.
Дополнительно сформулируем свойства операции 2 для алгебр Линденбаума нор-
мальных модальных логик.
Лемма 14.7. В алгебре Линденбаума нормальных модальных логик справедливы сле-
дующие свойства отношения порядка:
1) если [α] 6 [β], то 2[α ] 6 2[β],
2) ⊥ = [α ] ∧ ¬[α] является наименьшим элементом алгебры и 2⊥ 6 2[β] для про-
извольного элемента [β],
3) 2([α] ∧ [β] = 2[α] ∧ 2[β],
4) 2[α] ∨ 2[β] 6 2([α] ∨ [β]),
5) 2> = >.
Доказательство. Если [α] 6 [β], то формула α → β доказуема и по правилу Гёделя
доказуема формула 2(α → β). В силу аксиомы 2(α → β) → (2α → 2β) доказуема
формула 2α → 2β, т. е. 2[α] 6 2[β]. Свойство 2) следует из доказуемой формулы
α ∧ ¬α → β и свойства 1). Свойство 3) ранее было доказано. Свойство 4) вытекает
из аксиом A6, A7, H. Если α доказуемая формула, то 2α доказуемая формула. Из
аксиомы 2α → (β → 2α) следует доказуемость формулы β → 2α, что означает
2> = >. ¥
Вопросы и задания.
1. Построить алгебры Линденбаума для множеств формул от 1, 2, 3 и 4 перемен-
ных классической логики.
2. Построить алгебру Линденбаума для множества формул от n переменных класси-
ческой логики.
85

3. Каковы порядки построенных алгебр?
4. Построить алгебру Линденбаума для множества формул от n переменных пози-
тивной классической логики.
5. Каков порядок алгебры Линденбаума для множества формул от n переменных
позитивной классической логики?
15 Лекция 16. Допустимые правила вывода логики
Гейтинга
Мы рассмотрели ряд формальных систем логического вывода, в каждой из них по-
стулировалось незначительное число правил вывода, к которым для удобства постро-
ения выводов и доказательств мы добавили несколько доказуемых правил. Добав-
ление этих правил никак не изменило множества доказуемых формул, но позволило
быстрее находить доказательства и компактнее их излагать. В связи с этим возни-
кает интерес к таким правилам, которые можно применять в той или иной логике,
не меняя множества доказуемых формул. Такие правила мы назвали допустимыми.
Дадим более строгое определение допустимого правила.
Правило
r =
α
1
(p
1
, . . . , p
n
), . . . , α
k
(p
1
, . . . , p
n
)
β(p
1
, . . . , p
n
)
будем называть допустимым в логике Λ, если для любого набора формул ψ
1
, . . . , ψ
n
из того, что формулы α
1
(ψ
1
, . . . , ψ
n
), . . . , α
k
(ψ
1
, . . . , ψ
n
) принадлежат Λ следует, что
β(ψ
1
, . . . , ψ
n
) также принадлежит Λ.
Мы уже отмечали, что все доказуемые правила допустимы. Обратное оказывается
не всегда верно. В данной лекции рассмотрим примеры логик и допустимых но не
доказуемых правил.
Рассмотрим следующие правила:
1) правило Харропа
¬x → (y ∨ z)
(¬x → y) ∨ (¬x → z)
,
2) правило Леммона-Скотта
(¬¬x → x) → (x ∨ ¬x)
¬¬x ∨ ¬x
,
3) обобщённое правило Леммона-Скотта
(x → y) → (x ∨ ¬y)
¬¬x ∨ ¬y
,
4) правило Минца
(x → y) → (x ∨ z)
((x → y) → x) ∨ ((x → y) → z)
.
Лемма 15.1. Правило Харропа
¬x → (y ∨ z)
(¬x → y) ∨ (¬x → z)
является допустимым, но не доказуемым правилом в логике Гейтинга.
86
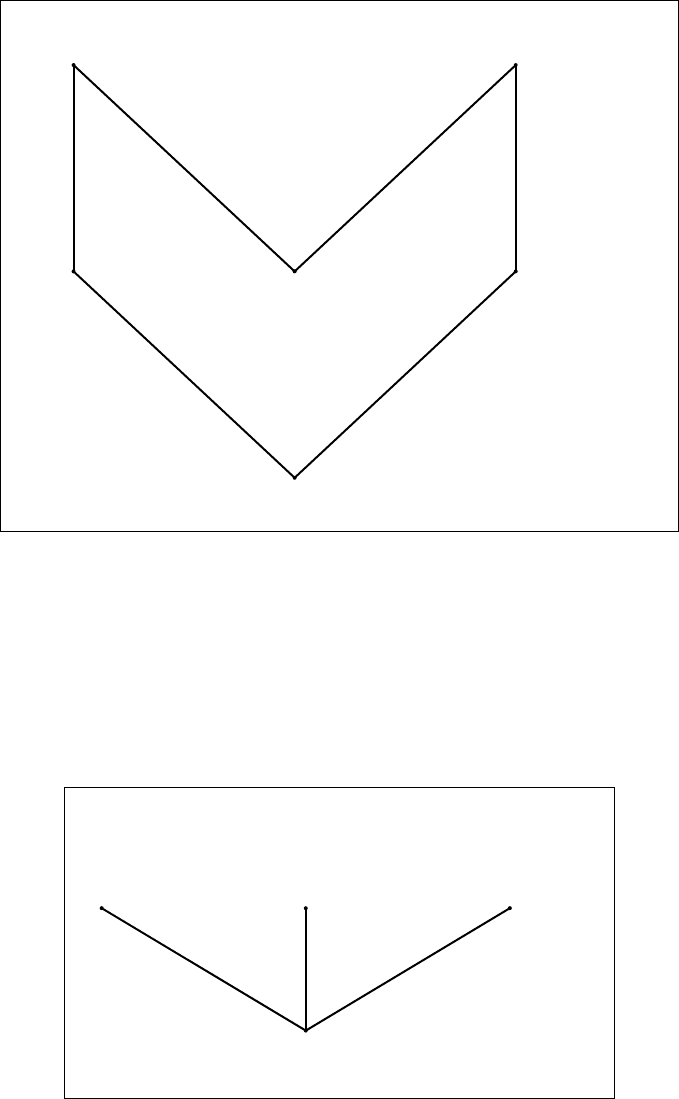
Предположим, что правило Харропа не допустимо в логике Гейтинга. Тогда су-
ществуют такие формулы α, β и γ, что ¬α → (β ∨ γ) ∈ Li, (¬α → β) ∨ (¬α →
γ) /∈ Li. Тогда для некоторого m в модели Ch
Li
(m) существует элемент a такой, что
a 1 (¬α → γ) ∨ (¬α → γ). Это означает, что существуют такие элементы a
1
и a
2
, что
a 6 a
1
, a 6 a
2
, a
1
1 ¬α → β, a
2
1 ¬α → γ. В соответствии с определением истинности
импликации в интуиционистской модели Крипке существуют такие элементы b
1
и b
2
,
что a
1
6 b
1
, a
2
6 b
2
, b
1
° ¬α, b
1
1 β, b
2
° ¬α, b
2
1 γ. По конструкции модели Ch
Li
(m)
существует конакрытие b множества {b
1
, b
2
}. Следовательно b ° ¬α и b 1 β ∨ γ, т.е.
b 1 ¬α → (β ∨ γ), что противоречит предположению ¬α → (β ∨ γ) ∈ Li.
a 1 (¬α → γ) ∨ (¬α → γ)
a
1
1 ¬α → β
a
2
1 ¬α → γ
b
1
° ¬α
b
1
1 β
b
2
° ¬α
b
2
1 γ
b ° ¬α
b 1 β ∨ γ
b 1 ¬α → (β ∨ γ)
Покажем далее, что правило не доказуемо. Для этого на некотором Li-фрейме
зададим означивание, при котором формула (¬x → (y ∨ z)) → ((¬x → y) ∨ (¬x →
z)) опровергается. Пусть F = {a, b
1
, b
2
, b
3
} Элементы {b
1
, b
2
, b
3
} являются макси-
мальными, элемент a - наименьший. Означивание V зададим следующим образом:
V (x) = {b
1
}, V (y) = {b
2
}, V (z) = {b
3
}. Так как только на точках b
2
и b
3
истин-
на формула ¬x и при этом b
2
° y ∨ z, b
3
° y ∨ z, то a ° ¬x → (y ∨ z). В то же
время b
2
1 ¬x → z, b
3
1 ¬x → y. Следовательно a 1 (¬x → y) ∨ (¬x → z) и
a 1 (¬x → (y ∨ z)) → ((¬x → y) ∨ (¬x → z)).
b
1
° x b
2
° y
b
2
° ¬x
b
2
° y ∨ z
b
2
1 ¬x → z
b
3
° y
b
3
° ¬x
b
3
° y ∨ z
b
3
1 ¬x → y
a ° ¬x → (y ∨ z)
a 1 (¬x → y ) ∨ (¬x → z)
Лемма доказана. ¥
87

Лемма 15.2. Правило Леммона-Скотта
(¬¬x → x) → (x ∨ ¬x)
¬¬x ∨ ¬x
является допустимым, но не доказуемым правилом в логике Гейтинга.
Предположим, что правило Леммона-Скотта не допустимо в логике Гейтинга.
Тогда существует такая формула α, что (¬¬α → α) → (α∨¬α) ∈ Li, (¬¬α∨¬α) /∈ Li.
Тогда для некоторого m в модели Ch
Li
(m) существует элемент a такой, что a 1
¬¬α ∨ ¬α. Это означает, что существуют такие элементы a
1
и a
2
, что a 6 a
1
, a 6
a
2
, a
1
° ¬α, a
2
° α. По конструкции модели Ch
Li
(m) существует конакрытие b
множества {a
1
, a
2
}. Следовательно b 1 ¬α и b 1 α, т.е. b 1 ¬α∨α. Так как a
1
° ¬α, то
a
1
1 ¬¬α и, следовательно, a
1
° ¬¬α → α. Так как a
2
° α, то также a
2
° ¬¬α → α.
Поскольку на элементе a
1
не опровергается ¬α, то b 1 ¬¬α и b ° ¬¬α → α. Таким
образом b 1 (¬¬α → α) → (¬α∨α), что противоречит предположению (¬¬α → α) →
(α ∨ ¬α) ∈ Li.
a 1 ¬¬α ∨ ¬α
a
1
° ¬α
a
1
1 ¬¬α
a
2
° α
a
2
° ¬¬α → α
b 1 α
b 1 ¬α
b 1 ¬α ∨ α
b 1 ¬¬α
b ° ¬¬α → α
Покажем далее, что правило не доказуемо. Для этого на некотором Li-фрейме
зададим означивание, при котором формула ((¬¬x → x) → (x ∨ ¬x)) → (¬¬x ∨ ¬x)
опровергается. Пусть F = {a, b
1
, b
2
, b
3
} фрейм, изображённый на рисунке. Положим
V (x) = {b
3
}. Тогда b
1
° ¬x, b
2
° ¬¬x и a 1 ¬¬x ∨ ¬x. Так как b
1
° ¬x, то b
1
1 ¬¬x
и, следовательно, b
1
° ¬¬x → x. Кроме того b
1
° x ∨ ¬x. Из того, что b
3
° x следует
b
3
° x ∨¬x, b
2
° ¬¬x, b
3
° ¬¬x → x, b
2
1 ¬¬x → x. Таким образом a ° (¬¬x → x) →
(x ∨ ¬x), что и приводит к утверждению a 1 ((¬¬x → x) → (x ∨ ¬x)) → (¬¬x ∨ ¬x).
88
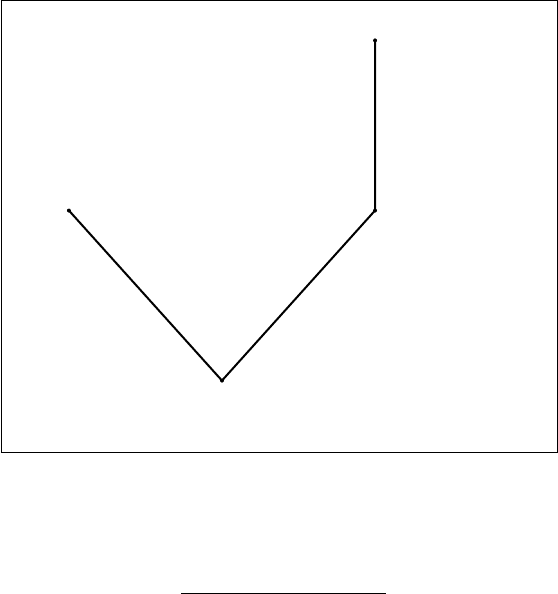
b
1
° ¬x
b
1
1 ¬¬x
b
1
° ¬¬x → x
b
1
° x ∨ ¬x
b
2
° ¬¬x
b
2
1 ¬¬x → x
b
3
° x
b
3
° x ∨ ¬x
b
3
° ¬¬x → x
a 1 ¬¬x ∨ ¬x
a ° (¬¬x → x) → (x ∨ ¬x)
Лемма доказана. ¥
Лемма 15.3. Обобщённое правило Леммона-Скотта
(x → y) → (x ∨ ¬y)
¬¬x ∨ ¬y
является допустимым, но не доказуемым правилом в логике Гейтинга.
Предположим, что обобщённое правило Леммона-Скотта не допустимо в логике
Гейтинга. Тогда существуют такие формулы α и β, что (α → β) → (α ∨ ¬β) ∈ Li,
(¬¬α ∨ ¬β) /∈ Li. Тогда для некоторого m в модели Ch
Li
(m) существует элемент a
такой, что a 1 ¬¬α ∨ ¬β. Это означает, что существуют такие элементы a
1
и a
2
,
что a 6 a
1
, a 6 a
2
, a
1
1 ¬¬α, a
2
1 ¬β. В соответствии с определением истинности
импликации в интуиционистской модели Крипке существуют такие элементы b
1
и b
2
,
что a
1
6 b
1
, a
2
6 b
2
, b
1
° ¬α, b
2
° β. По конструкции модели Ch
Li
(m) существует
конакрытие b множества {b
1
, b
2
}. Следовательно b 1 α и b 1 ¬β, т.е. b 1 α ∨ ¬β. В
то же время b
1
° α → β и b
2
° α → β. Следовательно b ° α → β, что противоречит
предположению (α → β) → (α ∨ ¬β) ∈ Li.
89
a 1 ¬¬α ∨ ¬β
a
1
1 ¬¬α a
2
1 ¬β
b
1
° ¬α
b
1
° α → β
b
2
° β
b
2
° α → β
b 1 α ∨ ¬β
b ° α → β
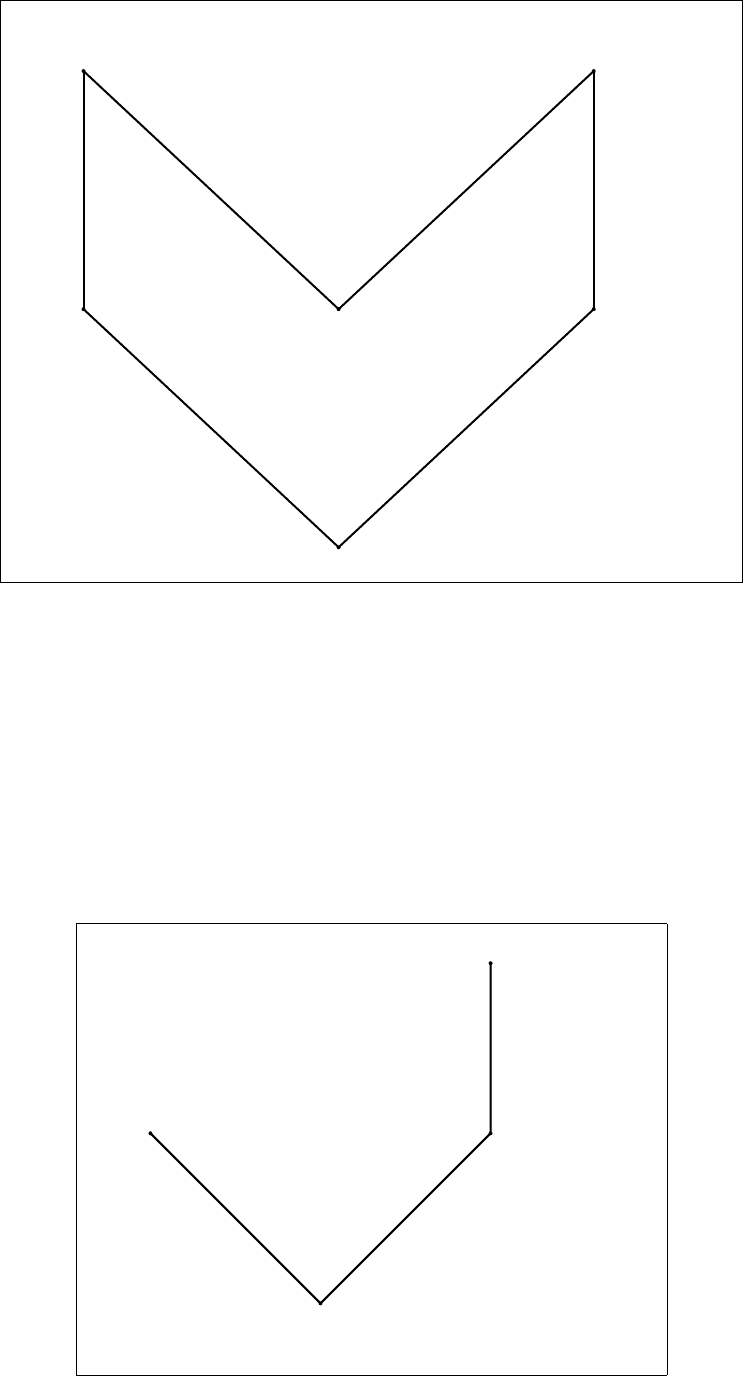
Покажем далее, что правило не доказуемо. Для этого на некотором Li-фрейме
зададим означивание, при котором формула ((x → y) → (x ∨ ¬y)) → (¬¬x ∨ ¬y)
опровергается. Пусть F = {a, b
1
, b
2
, b
3
}. Элементы {b
1
, b
3
} являются максимальны-
ми, элементы {b
1
, b
2
} несравнимы, b
2
< b
3
, элемент a - наименьший. Означивание V
зададим следующим образом: V (x) = {b
2
, b
3
}, V (y) = {b
3
}. При этом b
1
° ¬x, сле-
довательно a 1 ¬¬x. Так как b
3
° y, то a 1 ¬y. Таким образом a 1 ¬¬x ∨ ¬y. Так
как b
2
° x и b
2
1 y, то b
2
1 x → y. В то же время b
3
° x → y. Поскольку b
1
° ¬x,
то b
1
° x → y. Формула x → y истинна только на точках b
1
и b
3
. На этих же точках
истинна формула x ∨ ¬y, следовательно a ° (x → y) → (x ∨ ¬y). Итак формула
((x → y) → (x ∨ ¬y)) → (¬¬x ∨ ¬y) опровергается в точке a, т.е. правило не является
доказуемым.
b
1
1 x
b
1
° x → y
b
1
° x ∨ ¬y
b
2
° x
b
2
1 y
b
2
1 x → y
b
3
° x, b
3
° y
b
3
° x ∨ ¬y
b
3
° x → y
a 1 ¬¬x ∨ ¬y
a ° (x → y) → (x ∨ ¬y)
90
