Голованов М.И. Нестандартные логики. Реляционная семантика

Подождите немного. Документ загружается.

Лемма 15.4. Правило Минца

(x → y) → (x ∨ z)

((x → y) → x) ∨ ((x → y) → z)

является допустимым, но не доказуемым в логике Гейтинга правилом.

Доказательство. Предположим, что правило Минца не допустимо в логике Гей-

тинга. Тогда существуют такие формулы α, β и γ, что (α → β) → (α ∨ γ) ∈ Li,

((α → β) → α) ∨ ((α → β) → γ) /∈ Li. Тогда для некоторого m в модели Ch

(m)

существует элемент a такой, что a 1 ((α → β) → α) ∨ ((α → β) → γ). Это означает,

что существуют такие элементы a

и a

, что a 6 a

, a 6 a

, a

1 (α → β) → α,

1 (α → β) → γ. В соответствии с определением истинности импликации в интуи-

ционистской модели Крипке существуют такие элементы b

и b

, что a

6 b

, a

6 b

° α → β, b

1 α, b

° α → β, b

1 γ. По конструкции модели Ch

(m) суще-

ствует конакрытие b множества {b

, b

}. Следовательно b ° α → β и b 1 α ∨ γ, т.е.

b 1 (α → β) → (α ∨ γ), что противоречит предположению (α → β) → (α ∨ γ) ∈ Li.

a 1 ((α → β) → α) ∨ ((α → β) → β)

1 (α → β) → α a

1 (α → β) → γ

° α → β

1 α

1 γ

° α → β

b 1 α ∨ γ

b ° α → β

b 1 (α → β) → (α ∨ γ)

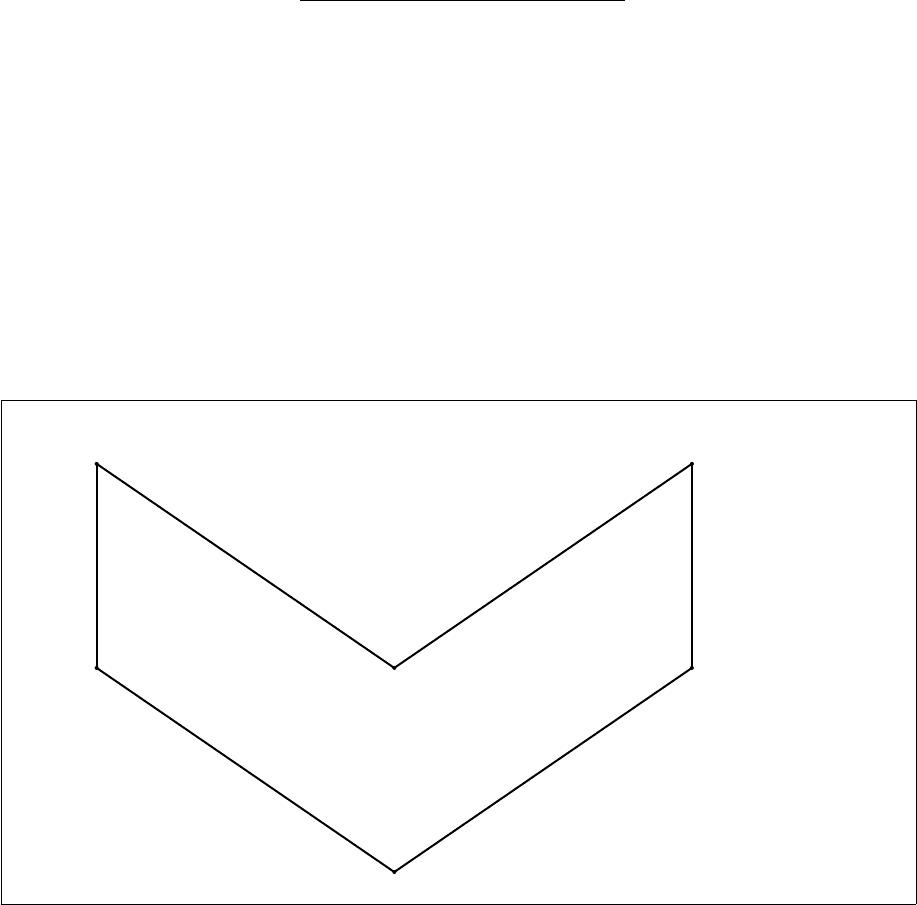
Покажем далее, что правило не доказуемо. Для этого на некотором Li-фрейме

зададим означивание, при котором формула ((x → y) → (x ∨ z)) → (((x → y) →

x) ∨ ((x → y) → z)) опровергается. Пусть F = {a, b

, b

} Элементы {b

, b

} явля-

ются максимальными, элемент a - наименьший. Означивание V зададим следующим

образом: V (x) = {b

, b

}, V (y) = {b

}, V (z) = {b

}. При этом формула x → y истинна

только в точках b

и b

. В этих же точках истьинна формула x ∨ z. Следовательно

a ° (x → y) → (x ∨ z). Поскольку b

° x → y и b

° x → y, но b

1 x, b

1 z, то a 1

(x → y) → x и a 1 (x → y) → z. Таким образом a ° ((x → y) → x) ∨ ((x → y) → z),

т.е. формула ((x → y) → (x ∨ z)) → (((x → y) → x) ∨ ((x → y) → z)) опровергается в

точке a.

° z

° x → y

° x ∨ z

1 (x → y) → x

° x

1 y

1 x → y

° x, b

° y

° x ∨ z

→

1 (x → y) → z

a 1 ((x → y) → x) ∨ ((x → y) → z)

a ° (x → y ) → (x ∨ z)

Лемма доказана. ¥

Вопросы и задания.

1. Привести пример интуиционистской логики, в которой правило Харропа не до-

пустимо.

2. Существуют ли табличные интуиционистские логики, в которых правило Харропа

не допустимо?

3. Привести пример интуиционистской логики, в которой правило Леммона-Скотта

не допустимо.

4. Существуют ли табличные интуиционистские логики, в которых правило Леммона-

Скотта не допустимо?

5. Будет ли правило Харропа допустимо во всякой интуиционистской логике глуби-

ны 2?

6. Будет ли правило Леммона-Скотта допустимо во всякой интуиционистской логике

глубины 2?

7. Сколько существует максимальных суперинтуиционистских логик, отличных от

классической, в которых все рассмотренные правила допустимы?

16 Лекция 17. Трансляция суперинтуиционистских

логик

Трансляцию Гёделя-Маккинси-Тарского, сопоставляющую каждой суперинтуицио-

нистской логике некоторую модальную логику определим индуктивно.

1. T (p) = 2p для любой переменной p,

2. T (α ∧ β) = T (α) ∧ T (β),

3. T (α ∨ β) = T (α) ∨ T (β),

4. T (α → β) = 2(T (α) → T (β)),

5. T (¬α) = 2¬T (α),

Лемма 16.1. Для любой формулы α, построенной с помощью связок ∧, ∨, →, ¬ в

логике S4 справедлива эквивалентность T (α) ≡ 2T (α).

Доказательство проведём индукцией по длине формулы.

I. Если формула α является пропозициональной переменной, то в силу п.1 опре-

деления трансляции T (p) = 2p. Так как 2T (p) = 22p, то в силу аксиом рефлексив-

ности и транзитивности имеем T (p) ≡ 2T (p).

II. Если формула α имеет вид β∧γ, то по п. определения трансляции T (α) = T (β)∧

T (γ). Поскольку формулы β и γ более короткие, чем α, то в силу предположения

индукции и свойств отношения эквивалентности в логике S4 T (β) ∧ T (γ) ≡ 2T (β) ∧

2T (γ) ≡ 22T (β) ∧ 22T (γ) ≡ 2(2T (β) ∧ 2T (γ)) ≡ 2(T (β) ∧ T (γ)) = 2T (α).

Если α = β ∨ γ, то 2T (α) = 2(T (β) ∨ T(γ)). В силу аксиомы рефлексивности

логики S4 имеем ` 2(T (β) ∨ T (γ)) → (T (β) ∨ T (γ)). По предположению индукции

T (β) ∨ T (γ) ≡ 2T (β) ∨ 2T (γ), т.е. ` 2(T(β) ∨ T (γ)) → (2T (β) ∨ 2T (γ)). В S4 имеем

` 2p ∨ 2q → 2(p ∨ q). В самом деле.

1. 2p → p аксиома,

2. p → p ∨ q аксиома A6,

3. 2p → p ∨ q из 1, 2 по правилу сечения,

4. 22p → 2(p ∨ q) из 3 по производному правилу,

5. 2p → 22p аксиома,

6. 2p → 2(p ∨ q) из 4, 5 по правилу сечения,

7. 2q → q аксиома,

8. q → p ∨ q аксиома A7,

9. 2q → p ∨ q из 7, 8 по правилу сечения,

10. 22q → 2(p ∨ q) из 9 по производному правилу,

11. 2q → 22q аксиома,

12. 2q → 2(p ∨ q) из 10, 11 по правилу сечения,

13. (2p → 2(p ∨ q)) → ((2q → 2(p ∨ q)) → (2p ∨ 2q → 2(p ∨ q)))

аксиома A8,

14. (2q → 2(p ∨ q)) → (2p ∨ 2q → 2(p ∨ q))

из 6, 13 по правилу m.p.,

15. 2p ∨ 2q → 2(p ∨ q) из 12, 14 по правилу m.p..

Выполнив соответствующую подстановку в доказанную формулу, получим обратную

импликацию ` 2T (β) ∨ 2T (γ) → 2(T (β) ∨ T (γ)).

В случае α = β → γ T (α) = 2(T (β) → T (γ)) ≡ 22(T (β) → T (γ)) = 2T (α). Если

α = ¬β, то T (α) = 2¬T (β) ≡ 22¬T (β) = 2T (α).

Пусть F = hW, Ri произвольный S4-фрейм, т.е. отношение R на множестве W

рефлексивно и транзитивно. Пусть W

- множество, элементами которого являются

сгустки фрейма F, а отношение на множестве сгустков определим следующим обра-

зом: для любых C

, C

∈ W

положим C

6 C

⇐⇒ ∃x ∈ C

, y ∈ C

(xRy). Данное

определение является корректным, т.е. не зависит от выбора элементов в сгустке,

так как для любых x, x

∈ C

, y, y

∈ C − 2 xRy ⇐⇒ x

. Заданное таким образом

отношение является отношением порядка. В самом деле, так как xRx, то для любого

сгустка C C 6 C. Если C

6 C

и C

6 C

, то в силу определения существуют такие

элементы x ∈ C

, y ∈ C

, z ∈ C

, что xRy и yRz. Так как отношение R транзитивно,

то xRz и следовательно C

6 C

. Если C

6 C

и C

6 C

, то в силу определения

существуют такие элементы x ∈ C

, y ∈ C

, что xRy и существуют такие элементы

z ∈ C

, t ∈ C

, что zRt. В силу определения сгустка имеем C

= C

. Построенный

таким образом фрейм F

= hW

, 6i будем называть каркасом фрейма F.

Пусть F = hW, Ri S4-фрейм и V - произвольное означивание переменных p

, . . . , p

на фрейме F. На фрейме F

определим означивание S переменных p

, . . . , p

следу-

ющим образом: C

⇐⇒ a °

. Во-первых, отметим, что означивание

S определено корректно. В самом деле, если b ∈ C

, то ∀x ∈ W (aRx ⇐⇒ bRx).

Следовательно ∀x ∈ W (a °

⇐⇒ b °

) и определение означивания не

зависит от выбора представителя в сгустке. Покажем далее, что построенное таким

образом означивание будет интуиционистским. Предположим C

и C

6 C

В соответствии с определением отношения 6 и свойствами S4-фреймов имеем aRb.

А так как в соответствии с определением означивания S a °

, то и b °

Следовательно C

, что и требовалось доказать. Таким образом мы сопоставили

каждой модели Крипке M = hW, R, V i для модальной S4-логики, где F = hW, Ri

S4-фрейм, интуиционистскую модель Крипке M

= hW

, 6, Si.

Отметим, что всякое частично упорядоченное множество является S4-фреймом.

Лемма 16.2. Для любой модели Крипке M = hW, R, V i, где F = hW, Ri S4-фрейм,

и любой формулы α в языке интуиционистской логики справедливо утверждение:

, C

) ° α ⇐⇒ (M, a) ° T (α).

Доказательство проведём индукцией по длине формулы α.

I. Пусть α = p, тогда по определению модели M

, C

) ° p ⇐⇒ (M, a) ° 2p.

II. а) Если α = α

∧ α

, то в силу определения конъюнкции

, C

) ° α

∧ α

⇐⇒ (M

, C

) ° α

и (M

, C

) ° α

В соответствии с предположением индукции

, C

) ° α

и (M

, C

) ° α

⇐⇒ (M, a) ° T (α

) и (M, a) ° T (α

Согласно определениям конъюнкции и трансляции имеем

(M, a) ° T (α

) и (M, a) ° T (α

) ⇐⇒ (M, a) ° T (α

∧ α

То есть в данном случае утверждение леммы верно.

б) Пусть

∨

. В этом случае в силу определения дизъюнкции

, C

) ° α

∨ α

⇐⇒ (M

, C

) ° α

или (M

, C

) ° α

В соответствии с предположением индукции

, C

) ° α

или (M

, C

) ° α

⇐⇒ (M, a) ° T (α

) или (M, a) ° T (α

Согласно определениям дизъюнкции и трансляции имеем

(M, a) ° T (α

) и (M, a) ° T (α

) ⇐⇒ (M, a) ° T (α

∨ α

То есть в данном случае утверждение леммы также верно.

в) Пусть α = α

→ α

и (M

, C

) ° α

→ α

. Пусть aRb и b ° T (α

). Тогда

6 C

. По предположению индукции C

° α

. По определению истинности импли-

кации в интуиционистской модели Крипке C

° α

. Вновь используя предположение

индукции, получаем b ° T (α

). Таким образом для всех достижимых из a элементов

b справедливо утверждение: b ° T (α

) → T (α

). То есть a ° 2(T (α

) → T (α

)), или

a ° T (α).

Обратно, предположим (M, a) ° T (α) и C

6 C

. В этом случае aRb и так как

T (α) = 2(T (α

) → T (α

)), то (M, b) ° T (α

) → T (α

). Пусть (M

, C

) ° α

. По

индуктивному предположению (M, b) ° T (α

). Так как (M, b) ° T (α

) → T (α

), то

(M, b) ° T(α

). Вновь используя индуктивное предположение, получаем (M

, C

) °

. Таким образом, для всякой точки C

, достижимой из C

справедливо утвержде-

ние: если (M

, C

) ° α

, то (M

, C

) ° α

, то есть (M

, C

) ° α.

г) Пусть α = ¬α

. Предположим C

° ¬α

и aRb, т.е. C

6 C

. Тогда C

1 α

и по

предположению индукции b 1 T (α

), т.е. b ° ¬T (α

) и a ° 2¬T (α

). Следовательно

a ° T (α).

Обратно, пусть a ° T (α), т.е. a ° 2¬T (α

) и C

6 C

. Тогда aRb и b ° ¬T (α

т.е. b 1 T (α

). По предположению индукции C

1 α

, т.е. C

° ¬α

= α, Что и

требовалось доказать.

Теорема 16.3. Для любой формулы α в языке интуиционистской логики справед-

ливо утверждение: α ∈ H ⇐⇒ T (α) ∈ S4.

Пусть α ∈ H. Предположим T (α) /∈ S4. Так как класс всех транзитивных ре-

флексивных фреймов является характеристическим для логики S4, то формула T (α)

опровергается на некотором S4-фрейме F при означивании V , т.е. в модели M =

hF, V i формула T (α) опровергается в некоторой точке a. Согласно лемме формула

α опровергается в точке C

модели M

= hF

, Si, что противоречит выбору α.

Пусть α /∈ H. Так как класс всех частично упорядоченных множеств является ха-

рактеристическим для логики H, то формула α опровергается на некотором частично

упорядоченном множестве hF, 6i при интуиционистском означивании V переменных

, . . . , p

формулы α. Так как отношение порядка является рефлексивным и транзи-

тивным отношением, то фрейм F = hF, 6i является S4-фреймом. Нетрудно видеть,

что при любом интуиционистском означивании V модель M = hF, V i совпадает с

моделью M

. Следовательно согласно лемме 16.2 можно утверждать, что для любой

точки a ∈ F модели M = hF, 6, V i и любой формулы ϕ в языке интуиционистской

логики (M, a) ° ϕ ⇐⇒ (M, a) ° T (ϕ).

Лемма доказана.

Вопросы и задания.

1. Построить трансляции следующих правил вывода:

p, q

p ∧ q

p → q, q → r

p → r

p → q

¬q → ¬p

p → q

(q → r ) → (p → r)

2. Существуют ли нормальные расширения логики S4, в которых допустимы не все

трансляции правил задачи 1?

3. Будут ли доказуемы в логике S4 трансляции правил задачи 1?

4. Будут ли доказуемы в логике K4 трансляции правил задачи 1?

5. Будут ли допустимы в логике K4 трансляции правил задачи 1?

6. Построить пример формулы, не являющейся трансляцией интуиционистской фор-

мулы.

7. Построить пример формулы, трансляция которой принадлежит S4, но не принад-

лежит K4.

17 Лекция 18. Допустимые правила вывода логики

S4 и её расширений

Рассмотрим трансляции Гёделя-Маккинси-Тарского правил вывода, допустимость

которых в логике Гейтинга доказана в лекции 16.

1) Трансляция правила Харропа

(

→

(

∨

))

2(2¬2x → 2y) ∨ 2(2¬2x → 2z)

2) трансляция правила Леммона-Скотта

(2(232x → 2x) → 2(2x ∨ 2¬2x))

232x ∨ 2¬2x

3) трансляция обобщённого правила Леммона-Скотта

2(2(2x → 2y) → (2x ∨ 2¬2y))

232x ∨ 2¬2y

4) трансляция правила Минца

2(2(2x → 2y) → (2x ∨ 2z))

2(2(2x → 2y) → 2x) ∨ 2(2(2x → 2y) → 2z)

Лемма 17.1. Трансляция правила Харропа

2(2¬2x → (2y ∨ 2 z))

2(2¬2x → 2y) ∨ 2(2¬2x → 2z)

является допустимым, но не доказуемым правилом в логиках K4, S4, Grz и GL.

Предположим, что трансляция правила Харропа не допустима в логике Λ, где Λ

одна из указанных в лемме логик. Тогда существуют такие формулы α, β и γ, что

2(2¬2α → (2β ∨ 2γ)) ∈ Li, 2(2¬2α → 2β) ∨ 2(2¬2α → 2γ) /∈ Li. Тогда для

некоторого m в модели Ch

(m) существует элемент a такой, что a 1 2(2¬2α →

2β)∨2(2¬2α → 2γ), то есть a 1 2(2¬2α → 2β) и a 1 2(2¬2α → 2γ). В соответ-

ствии с определением истинности связки 2 в модели Крипке это означает, что суще-

ствуют такие элементы a

и a

, что aRa

, aRa

, a

1 2¬2α → 2β, a

1 2¬2α → 2γ.

То есть a

° 2¬2α, a

1 2β, a

° 2¬2α, a

1 2γ. По определению связки 2 на

любом элементе u, достижимом из a

, истинна формула ¬2α и существует элемент

, достижимый из a

, на котором опровергается формула β. Аналогичные рассуж-

дения справедливы для элемента a

. Таким образом существуют такие элементы

и b

, что a

, a

, b

° 2¬2α ∧ ¬2α, b

1 β, b

° 2¬2α ∧ ¬2α, b

1 γ.

По построению модели Ch

(m) существует рефлексивное (в S4 и Grz) или ирре-

флексивное (в K4 и GL) конакрытие b множества сгустков {C

, C

}, содержащих,

соответственно, элементы b

и b

. Следовательно b ° 2¬2α и b 1 2β ∨ 2γ, т.е.

b 1 2¬2α → (2β ∨ 2γ). Так как по построению модели Ch

(m) элемент b имеет

предшественника b

, то b

1 2(2¬2α → (2β ∨ 2γ)) что противоречит предположе-

нию 2(2¬2α → (2β ∨ 2γ)) ∈ Λ.

a 1 (2(2¬2α → 2β) ∨ 2(2¬2α → 2γ)

1 2(2¬2α → 2β)

1 2(2¬2α → 2γ)

° 2¬2α ∧ ¬2α

1 β

° 2¬2α ∧ ¬2α

1 γ

b ° 2¬2α

b 1 2β ∨ 2γ

b 1 2¬2α → (2β ∨ 2γ)

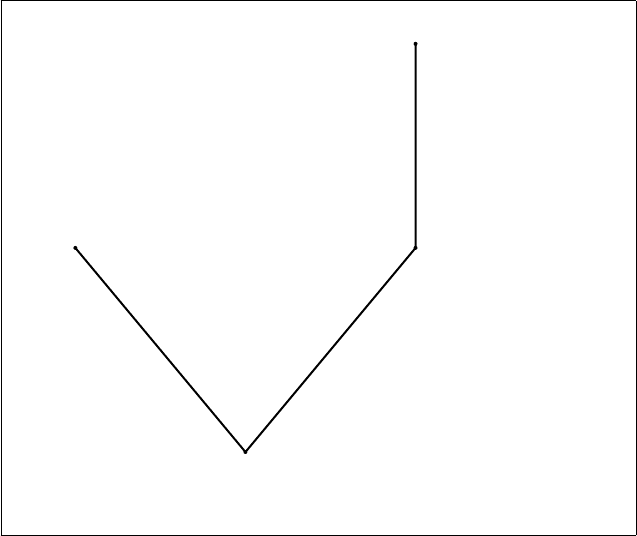
Покажем далее, что трансляция правила Харропа не доказуема в указанных ло-

гиках. Доказательство проведём отдельно: а) для рефлексивных логик S4 и Grz, и

б) для нерефлексивных логик K4 и GL. Впрочем, для логики K4 оба доказательства

справедливы.

а) В силу теоремы дедукции для расширений логики S4 справедливо утвержде-

ние: ψ ` ϕ ⇐⇒ ` 2ψ → ϕ. Для опровержения доказуемости трансляции прави-

ла Харропа в S4 и Grz построим Λ-фрейм и зададим такое означивание, что фор-

мула 22(2¬2x → (2y ∨ 2z)) → (2(2¬2x → 2y) ∨ 2(2¬2x → 2z)) ложна в

некоторой точке Λ-фрейма. Пусть F = {a, b

, b

}. Элементы {b

, b

} являются

максимальными, элемент a - наименьший, все элементы рефлексивны. Означива-

ние V зададим следующим образом: V (x) = {b

}, V (y) = {b

}, V (z) = {b

}. Так

как только на точках b

и b

истинна формула 2¬2x и при этом b

° 2y ∨ 2z,

° 2y ∨ 2z, то a ° 2(2¬2x → (2y ∨ 2z)). В то же время b

1 2¬2x → 2z,

1 2¬2x → 2y. Следовательно a 1 2(2¬2x → 2y) ∨ 2(2¬2x → 2z) и поэтому

a 1 2(2¬2x → (2y ∨2z)) → (2(2¬2x → 2y)∨2(2¬2x → 2z)). Поскольку точка a

рефлексивна, то a 1 22(2¬2x → (2y ∨ 2z)) → (2(2¬2x → 2y) ∨ 2(2¬2x → 2z)).

° 2x b

° 2y b

° 2¬2x

° 2y ∨ 2z

1 2(2¬2x2 → 2z)

° 2z

° 2¬2x

° 2y ∨ 2z

1 2(2¬2x → 2y)

a ° 2(2¬2x → ( 2y ∨ 2z))

a 1 2(2¬2x → 2y) ∨ 2(2¬2x → 2z)

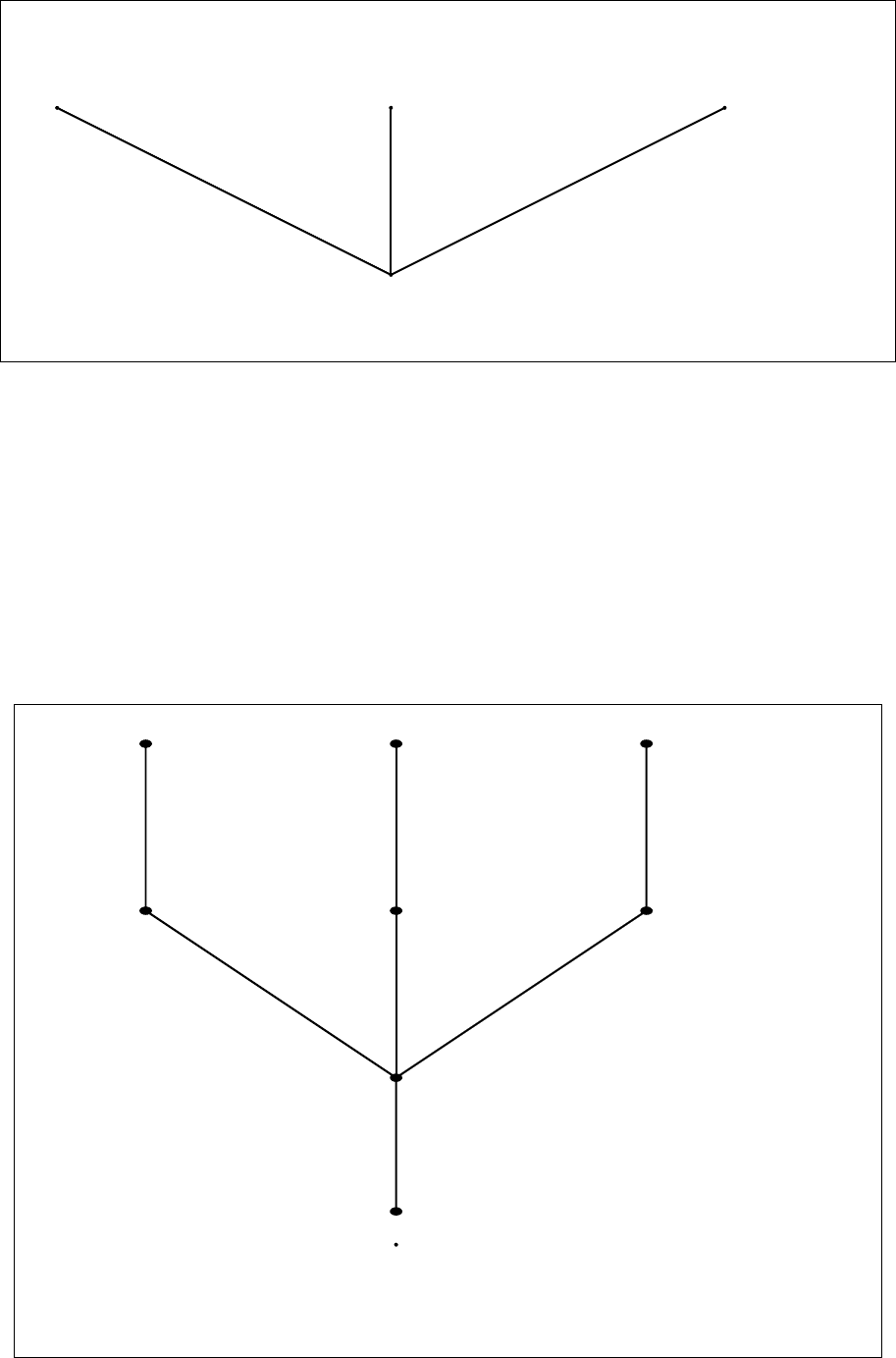
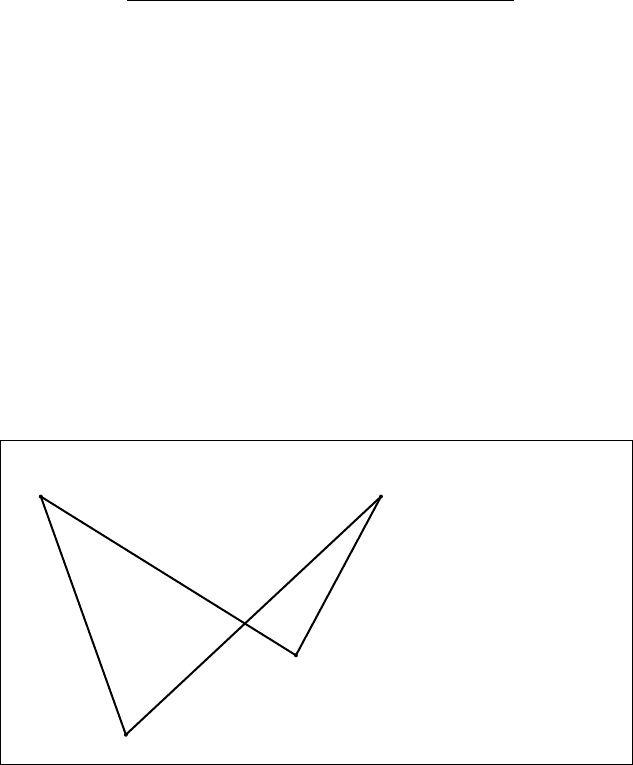
б) В силу теоремы дедукции для расширений логики K4 справедливо утвержде-

ние: ψ ` ϕ ⇐⇒ ` ψ ∧ 2ψ → ϕ. Для опровержения доказуемости трансляции пра-

вила Харропа в логиках K4 и GL на фрейме F = {a

, a

, b

, c

, d

}, состо-

ящем из иррефлексивных элементов, отношение R определим так как изображе-

но на рисунке, а означивание возьмём следующее: V (x) = {b

, b

}, V (y) = {c

, c

V (z) = {d

, d

}. Так как только на точках c

, c

и d

, d

истинна формула 2¬2x и при

этом c

° 2y ∨ 2z, d

° 2y ∨ 2z, то a

° 2(2¬2x → (2y ∨ 2z)) и a

° 22(2¬2x →

(2y ∨ 2z)). В то же время c

1 2¬2x → 2z, d

1 2¬2x → 2y. Следовательно

1 2(2¬2x → 2y) ∨ 2(2¬2x → 2z) и a

1 2(2¬2x → 2y) ∨ 2(2¬2x → 2z).

Поэтому a

1 2 (2¬2x → (2y ∨ 2z)) → (2(2¬2x → 2y) ∨ 2(2¬2x → 2z)),

1 22(2¬2x → (2y ∨ 2z)) → ( 2(2¬ 2x → 2y) ∨ 2(2¬2x → 2z)). Отсюда в силу

теоремы дедукции следует 2(2¬2x → (2y∨2z)) 0 2(2¬2x → 2y)∨2(2¬2x → 2z).

° 2x c

° 2y c

° 2¬2x

° 2y ∨ 2z

1 2(2¬2x2 → 2z)

° 2z

° 2¬2x

° 2y ∨ 2z

1 2(2¬2x → 2y)

° 2(2¬2x → (2y ∨ 2z))

1 2(2¬2x → 2y) ∨ 2(2¬2x → 2z)

° 2(2¬2x → (2y ∨ 2z))

° 22(2¬2x → (2y ∨ 2z))

Лемма доказана. ¥

Лемма 17.2. 1. Трансляция правила Леммона-Скотта

2(2(232x → 2x) → (2x ∨ 2¬2x))

232x ∨ 2¬2x

является допустимым, но не доказуемым правилом в логиках S4, Grz и S4.1.

2. Трансляция правила Леммона-Скотта не является допустимым правилом в ло-

гике GL.

1. Предположим, что правило Леммона-Скотта не допустимо в логиках S4, Grz

и S4.1. Тогда существует такая формула α, что (232α → 2α) → (α ∨ ¬α) ∈ Li,

(232α∨ 2¬2α) /∈ Li. Тогда для некоторого m в модели Ch

(m) существует элемент

a такой, что a 1 232α ∨ 2¬2α. Это означает, что существуют такие элементы a

, что aRa

, aRa

, a

° 2¬2α, a

° 2α. По конструкции модели Ch

(m) существует

конакрытие b множества {C

, C

}, где C

, C

- сгустки, содержащие, соответственно,

элементы a

и a

. Так как a

° 2¬2α, то a

1 232α. Так как a

° 2α, то a

2(232α → 2α). Таким образом b ° 2(232α → 2α ). Поскольку a

1 232α и

1 2¬2α, то b ° 232α ∨ 2¬2α и посылка правила опровергается на модели

(m) вопреки предположению.

a 1 232α ∨ 2¬2α

° 2¬2α

1 232α

° 2α

° 2(232α → 2α)

b ° 2(232α → 2α)

b 1 232α ∨ 2¬2α

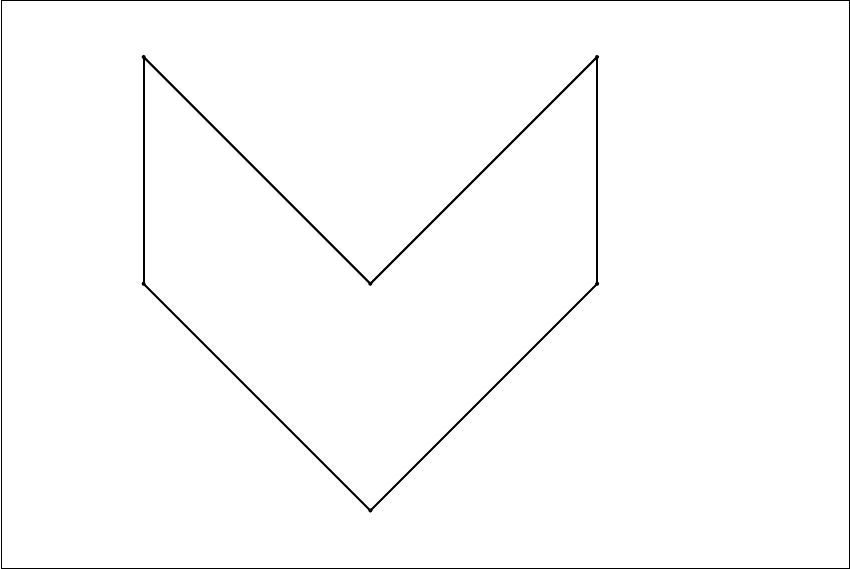
Покажем далее, что правило не доказуемо в логиках S4, Grz и S4.1. Для этого на

некотором Λ-фрейме зададим означивание, при котором формула 22(2(232x →

)

→

(

∨

))

→

(

232

∨

)

опровергается. Пусть

{

a, b

, b

}

фрейм, изображённый на рисунке. Положим V (x) = {b

}. Тогда b

° 2¬2x, b

232x и a 1 232x ∨ 2¬2x. Так как b

° 2¬2x, то b

1 232x и, следовательно,

° 2(232x → 2x). Кроме того b

° 2x ∨ 2¬2x. Из того, что b

° 2x следует

° 2x ∨ 2¬2x, b

° 232x, b

° 2(232x → 2x), b

1 232x → 2x. Таким

образом a ° 2(2(232x → 2x) → (2x ∨ 2¬2x)), что и приводит к утверждению

a 1 2(2(232x → 2x) → (2x ∨ 2¬ 2x)) → (232x ∨ 2¬2x). Так как в расширениях

логики S4 2α ≡ 22α, то из предыдущего утверждения следует, что правило не

доказуемо в логиках S4, Grz и S4.1.

° 2¬2x

1 232x

° 2(232x → 2x)

° 2x ∨ 2¬2x

° 232x

1 232x → 2x

° 2x

° 2x ∨ 2¬2x

° 2(232x → 2x)

a 1 232x ∨ 2¬2x

a ° 2(2(232x → 2x) → (2x ∨ 2¬2x))

Для доказательства второго утверждения положим x = >. Так как на модели

(m) формула 2> всюду истинна, то посылка рассматриваемого правила при-

надлежит логике GL. Поскольку первый слой модели Ch

(m) состоит из иррефлек-

сивных точек, то на втором слое формула 232x ∨ 2¬2x опровергается при любых

значениях переменной x.

Лемма доказана. ¥

Лемма 17.3. Трансляция обобщённого правила Леммона-Скотта

2(2(2x → 2y) → (2x ∨ 2¬2y))

232x ∨ 2¬2y

является допустимым, но не доказуемым правилом в логике Grz.

Предположим, что трансляция обобщённого правила Леммона-Скотта не допу-

стима в логике Grz. Тогда существуют такие формулы α и β, что 2(2(2α → 2β) →

(2α ∨ 2¬2β)) ∈ Grz, 232α ∨ 2¬2β /∈ Grz. Тогда для некоторого m в модели

Grz

(m) существует элемент a такой, что a 1 232α ∨ 2¬2β. Это означает, что

существуют такие элементы a

и a

, что aRa

, aRa

, a

1 232α , a

1 2¬2β. В соот-

ветствии с определением операции 2 в модели Крипке существуют такие элементы

и b

, что a

, a

, b

° 2¬2α, b

° 2β. Следовательно в любой точке u, до-

стижимой из b

, формула 2α опровергается, т.е. u ° 2α → 2β и b

° 2(2α → 2β).

В силу транзитивности отношения R на любой точке u, достижимой из b

, формула

2β истинна, поэтому u ° 2α → 2β и b

° 2(2α → 2β). По конструкции модели

Grz

(m) существует конакрытие b множества {b

, b

}. Так как b

достижима из b и

1 2α, то b 1 2α и следовательно b ° 2α → 2β. Таким образом b ° 2(2α → 2β).

Так как b

1 2α и b

° 2β, то b 1 2α ∨ 2¬2β.

Следовательно b 1 2(2α → 2β) → (2α∨2¬2β). Так как отношение достижимо-

сти в логике Grz является рефлексивным, то полученное утверждение противоречит

предположению 2(2(2α → 2β) → (2α ∨ 2¬2β)) ∈ Grz. Таким образом правило

допустимо в Grz.

100