Голованов М.И. Нестандартные логики. Реляционная семантика
Подождите немного. Документ загружается.

a 1 232α ∨ 2¬2β
a
1
1 232α a
2
1 2¬2β
b
1
° 2¬2α
b
1
° 2(2α → 2β)
b
2
° 2β
b
2
° 2(2α → 2β)
b 1 2α ∨ 2¬2β
b ° 2(2α → 2β)
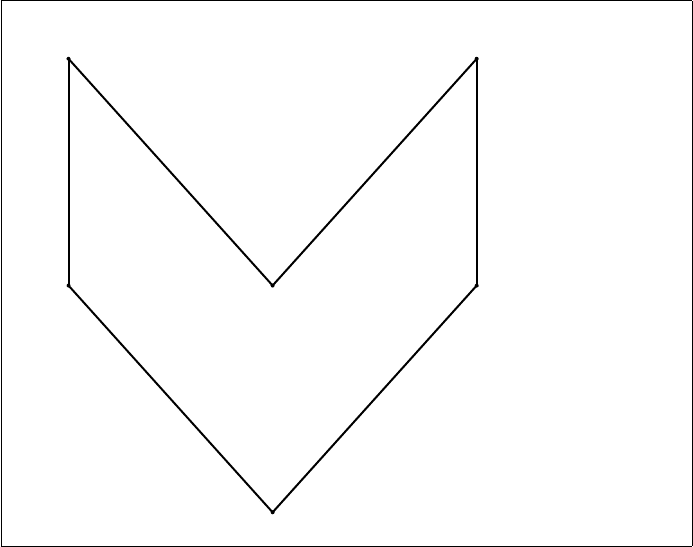
Покажем далее, что правило не доказуемо. Для этого на некотором Grz-фрейме
зададим означивание, при котором формула 2(2(2x → 2y) → (2x ∨ 2¬2y)) →
(232x ∨ 2¬2y) опровергается. Пусть F = {a, b
1
, b
2
, b
3
}. Элементы {b
1
, b
3
} являются
максимальными, элементы {b
1
, b
2
} несравнимы, b
2
< b
3
, элемент a - наименьший.
Означивание V зададим следующим образом: V (x) = {b
2
, b
3
}, V (y) = {b
3
}. При этом
b
1
° 2¬2x, следовательно a 1 232x. Так как b
3
° 2y, то a 1 2¬2y. Таким
образом a 1 232x ∨ 2¬2y. Так как b
2
° 2x и b
2
1 2y, то b
2
1 2x → 2y. В то
же время b
3
° 2x → 2y. Поскольку b
1
° ¬2x, то b
1
° 2x → 2y. Формула 2(2x →
2y) истинна только на точках b
1
и b
3
. На этих же точках истинна формула 2x ∨
2¬2y, следовательно a ° 2(2(2x → 2y) → (2x ∨ 2¬2y)) и в силу транзитивности
отношения достижимости a ° 22(2(2x → 2y) → (2x ∨ 2¬2y)). Итак формула
22(2(2x → 2y) → (2x ∨ 2¬2y)) → (232x ∨ 2¬2y) опровергается в точке a, т.е.
правило не является доказуемым.
101
b
1
° 2¬2x
b
1
° x → y
b
1
° x ∨ ¬y
b
2
° 2x
b
2
1 2y
b
2
1 2x → 2y
b
3
° 2x, b
3
° 2y
b
3
° 2x ∨ 2¬2y
b
3
° 2x → 2y
a 1 232x ∨ 2¬2y
a ° 2(2(2x → 2y) → (2x ∨ 2¬2y))
Лемма доказана.
¥
Вопросы и задания.
1. Привести пример модальной логики, в которой правило Харропа не допустимо.
2. Существуют ли табличные модальные логики, в которых правило Харропа не до-
пустимо?
3. Привести пример модальной логики, в которой правило Леммона-Скотта не допу-
стимо.
4. Существуют ли табличные модальные логики, в которых правило Леммона-Скотта
не допустимо?
5. Будет ли правило Харропа допустимо во всякой нормальной модальной логике
глубины 2?
6. Будет ли правило Леммона-Скотта допустимо во всякой модальной логике глуби-
ны 2?
7. Сколько существует максимальных модальных логик, в которых 2p p и все
рассмотренные правила допустимы?
102
Содержание
1 Лекция 1. Введение. Краткий экскурс в историю логических иссле-
дований. 2
2 Лекция 2. Определение пропозициональной логики. 6
2.1 Позитивная логика . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3 Лекция 3. Основные теоремы позитивной логики. 11
4 Лекция 4. Немодальные расширения позитивной логики. 21
4.1 Расширение логики Lp с помощью константы ⊥ . . . . . . . . . . . . . 21
4.2 Расширение логики Lp с помощью связки ¬ . . . . . . . . . . . . . . . . 22
4.3 Трансляции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
5 Лекция 5. Свойства некоторых расширений логики Lp 28
6 Лекция 6. Модальные логики, нормальные модальные логики. 33
6.1 Наименьшая нормальная модальная логика . . . . . . . . . . . . . . . . 33
6.2 Нормальные расширения логики K . . . . . . . . . . . . . . . . . . . . 37
7 Лекция 7. Основные классы пропозициональных логик 40
8 Лекция 9. Семантика Крипке для суперинтуиционистских логик 44
9 Лекция 10. Характеристические классы фреймов для модальных ло-
гик K, T, S4, S5 и суперинтуиционистских логик H, KC, LC 52
10 Лекция 11. Метод фильтрации 58
11 Лекция 12. Характеристические классы фреймов для некоторых рас-
ширений модальных логик K, T , K4, S4 63
12 Лекция 13. Специальные модели Крипке для модальных логик. 69
13 Лекция 14. Временные логики, семантика Крипке для временных
логик 75
14 Лекция 15. Алгебра Линденбаума 81
15 Лекция 16. Допустимые правила вывода логики Гейтинга 86
16 Лекция 17. Трансляция суперинтуиционистских логик 92
17 Лекция 18. Допустимые правила вывода логики S4 и её расшире-
ний 96
103
