Голичев И.И. Лабораторный практикум по курсу «Численные методы»

Варианты заданий.

Найти корень уравнения

 

0xf

.

№

варианта

(x) a b c

1 2 3 4 5

1

bxtgax 

1.2618 1.8433 –

2 2.5237 3.6866 –

3 3.47 5.0691 –

4 8.8328 12.903 –

5 7.571 11.06 –

6 5.6782 8.2949 –

7

 

cbxax ln

1.2195 1.3744 0.5

8 2.7439 3.0924 1.0

9 3.6585 4.1232 1.5

10 4.2683 4.8104 2.0

11 5.7927 6.5284 2.5

12 7.3171 8.2402 3.0

1 2 3 4 5

13

cxbxa sin

2.33 2.857 2

14 4 3.8125 3.25

15 5.33 4.59 4.25

16 6 4.99 4.75

17 7 5.5857 5.5

18 9.667 7.176 7.5

19

xae

bx



0.0714 0.933 –

20 0.3889 0.72 –

21 0.5476 0.6462 –

22 0.6304 0.6133 –

23 0.7 0.5882 –

24 0.8103 0.5524 –

25 0.875 0.533 –

26 0.9118 0.5231 –

27 0.9595 0.5103 –

21

Лабораторная работа № 7.

Решение системы нелинейных уравнений

методом Ньютона

Рассмотрим систему

n

нелинейных уравнений с

n

неизвестными

 

0,...,

11



n

xxf

,

 

0,...,

12



n

xxf

, (1)

……………

 

0,...,

1



nn

xxf

или в векторной форме

 

0xf

, (1’)

где















n

f

f 

1

,















n

x

x 

1

.

Основная идея метода Ньютона состоит в выделении из уравнений

системы линейных частей, которые являются главными при малых

приращениях аргументов. Это позволяет свести исходную задачу к решению

последовательности линейных систем.

Пусть известно некоторое приближение

 

k

x

корня

*

x

. Тогда поправку

 

k

xxx 

*

можно найти, решая систему

 

0 xxf

k

.

Для определения

x

разложим векторную функцию

f

в ряд по

x

. Сохранив

только линейные по

x

части, получим

fx

x

f

















,

здесь через















x

f

обозначена матрица производных

j

i

ij

x

f

x

f



















, если

0det 















x

f

, то

f

x

f

x

1

















, где

1















x

f

– матрица, обратная матрице производных.

Таким образом, последовательные приближения корня можно вычислять

по формуле

     

kkk

xxx 

1

.

Отсюда видно, что метод Ньютона решения системы (1) состоит в

построении итерационной последовательности

   

 

k

xx

kk

xf

x

f

xx

k























1

. (2)

Если

0det 















x

f

, то в достаточно малой окрестности корня

*

x

итерационный процесс (2) сходится, причём с квадратичной скоростью, т.е.

     

*1

2

1

xxxx

kkk





.

Если начальное приближение выбрано удачно, то метод Ньютона

сходится очень быстро. Поэтому в качестве критерия окончания итерационного

процесса можно использовать условие

   







2

1 kk

xx

.

22

Задание. Решить систему нелинейных уравнений.

Порядок выполнения лабораторной работы на ЭВМ.

1. Определить из геометрических соображений начальное приближение

решения.

2. Составить подпрограмму F и G вычисления значений

f

и















x

f

.

3. Составить головную программу.

4. Провести вычисления на ЭВМ.

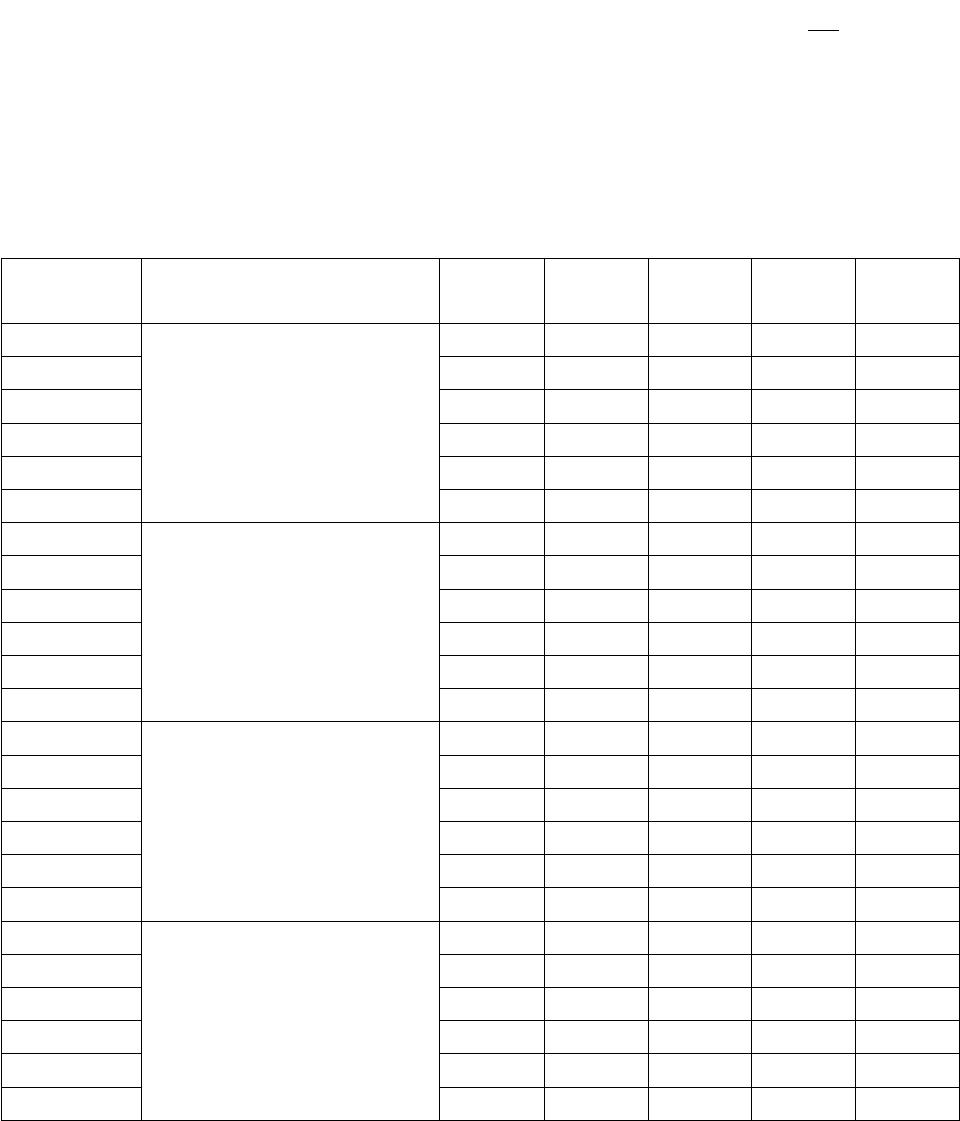
Варианты заданий.

Решить систему уравнений

 









0,

,0,

yxg

yxf

при заданных значениях коэффициентов.

№

варианта

a b c d e

1

 

xbyyxg

tgxyaxyxf

ln,

,,

2





1.0 7.5

2 2.0 6.0

3 3.0 4.6

4 4.0 3.0

5 5.0 1.5

6 6.0 2.0

7

 

cxyyxg

yxbyaxyxf





cos,

,,

2

0.16 2.1 1.0

8 0.24 3.5 2.0

9 0.32 4.9 3.0

10 0.40 5.3 4.0

11 0.48 6.7 5.0

12 0.60 7.5 6.0

13

   

exdyyxg

cbyaxyxf





cos,

,sin,

0.4 3.5 –1.5 0.2 0.5

14 0.8 2.0 –1.0 0.6 0.6

15 1.2 0.5 –0.5 0.8 0.7

16 1.6 –1.0 0 1.2 0.8

17 1.8 –2.0 0.1 1.6 0.8

18 2.1 –3.0 0.4 1.8 1.2

19

 

34,

,cos,

23





xxcyyxg

bytgaxyxf

1.0 1.5 2.0

20 2.0 2.0 2.1

21 3.0 2.5 2.2

22 4.0 3.0 2.3

23 5.0 3.5 2.4

24 6.0 4.0 2.5

Лабораторная работа № 8.

Приближённое решение задачи Коши

методом Эйлера

23

Пусть требуется найти приближённое решение дифференциального

уравнения

 

yxfy ,'

, удовлетворяющее начальному условию

 

00

yxy 

.

Численное решение задачи состоит в построении таблицы приближённых

значений

n

yyy ,...,,

21

решения уравнения

 

xy

в точках

n

xxx ,...,,

21

. Чаще всего

,...2,1,0,

0

 iihxx

i

(1)

Этот метод относится к группе одношаговых методов, в которых для

расчёта точки

 

11

;

 ii

yx

требуется информация только о последней

вычисленной точке

 

ii

yx ;

. Метод допускает простую геометрическую

интерпретацию (рис. 3). Предположим, что известна точка

 

ii

yx ;

, определяется

уравнением

 

iii

xxyyy  '

,(в скобках не равно, а минус) а так как

 

iii

yxfy ,' 

и

hxx

ii



1

, то

 

iiii

yxhfyy ,

1





. Для оценки погрешности метода на одном

шаге сетки разложим точное решение в ряд Тейлора в окрестности узла

i

x

:

       

 

   

 

22

1

,' hOyxhfxyhOhxyxyhxyxy

iiiiiii





. (2)

Сравнение формулы (1) с разложением (2) показывает, что они согласуются до

членов первого порядка по

h

, а погрешность формулы (1) равна

 

2

hO

. Если

расчётные формулы численного метода согласуются с порядком метода. Таким

образом, метод Эйлера – метод первого порядка.

Метод Эйлера легко обобщается на случай нормальных систем

дифференциальных уравнений. Пусть требуется найти решение системы

дифференциальных уравнений

 

,,...,,'

................................

,,...,,'

1

11

nnn

ni

yyxfy



удовлетворяющее начальным условиям

     

0020021001

,...,,

nn

yxyyxyyxy 

. Или

в векторной форме:

 

YxfY ,'

,

 

00

YxY 

,

          

02010021

,...,,,,...,,

nn

yyyYxyxyxyxY 

.

Приближённые значения

ki

y

точного решения

 

ik

xy

в точках

i

x

вычисляются

по формулам

     

 

1121111

,...,,,





iniiikkiki

yyyxhfyy

,

nk ,...,2,1

,

,...2,1i

Задание. Составить программу решения задачи Коши для заданной системы

дифференциальных уравнений второго порядка. Результаты печатать на

каждом шаге.

Порядок выполнения лабораторной работы на ЭВМ.

1. Составить головную программу.

2. Составить подпрограмму вычисления правых частей P(X,Y,F) уравнений

системы.

3. Произвести вычисления на ЭВМ.

24

Варианты заданий.

Решить на отрезке

 

3,0

с шагом

0,1

задачу Коши

для системы второго порядка

 





















.0

,00

.,,

,

202

1

21

2

1

yy

y

yyxf

dx

dy

y

dx

dy

№

варианта

 

21

,, yyxf

a

20

y

1

x

ae

8.0



0.01 0.5

2 0.02 1/3

3 0.03 0.25

4 0.04 0.2

5 0.05 1/6

6 0.06 1/7

7 0.07 0.125

8 0.08 1/9

9 0.09 0.1

10

12

yaxy 

0.01 0.2

11 0.02 0.33

12 0.03 0.25

13 0.04 0.2

14 0.05 1/6

15

x

eay



1

0.01 0.5

16 0.02 1/3

17 0.03 0.25

18

x

e

2.1

04.0



– 0.2

19

x

e

8.0

04.0



– 0.2

20

1

2

yxaxy 

0.01 0.5

21 0.02 1/3

22 0.03 0.25

23 0.04 0.2

24 0.05 1/6

25 0.06 1/7

25

Лабораторная работа № 9.

Приближённое решение задачи Коши

методом Рунге

-

Кутта

Пусть требуется найти решение дифференциального уравнения

 

yxfy ,'

, удовлетворяющее начальному условию

 

00

yxy 

.

Численное решение задачи состоит в построении таблицы приближённых

значений

n

yyy ,...,,

21

решения уравнения

 

xy

в точках

n

xxx ,...,,

21

. Точки

n

xxx ,...,,

21

– узлы сетки. Используем систему равноотстоящих узлов. Величина

h

– шаг сетки

 

0h

.

Методом Рунге

-

Кутта в литературе обычно называют одношаговый

метод четвёртого порядка, относящийся к широкому классу методов типа Рунге

-

Кутта. В этом методе величины

1i

y

вычисляют по следующим формулам:

 

   

 

1 1 2 3 4

1 2 1

3 2

4 3

6 2 2 ,

, , 2; 2 ,

2; 2 ,

; .

i i

i i i i

i i

y y h k k k k

k f x y k f x h y hk

k f x h y hk



    

   

  

(1)

Погрешность метода на одном шаге сетки равна

5

Mh

, но поскольку на

практике оценить величину

M

обычно трудно, при оценке погрешности

используют правило Рунге. Для этого проводят вычисления сначала с шагом

h

,

а затем – с шагом

2h

, то справедлива оценка

 

   

h

i

h

ii

h

i

yyxyy 

22

15

16

.

При реализации метода на ЭВМ обычно на каждом шаге делают двойной

пересчёт. Если полученные значения отличаются в пределах допустимой

погрешности, то шаг

h

удваивают. В противном случае берут половинный шаг.

Метод Рунге

-

Кутта легко переносится на нормальные системы

дифференциальных уравнений вида

   

,,...,,,'

21 nkk

yyyxfxy 

nk 1

,

которые для краткости удобно записывать в векторной форме:

       

nn

ffffyyyyyxfxy ,...,,,,...,,,,'

2121



.

Для получения расчётных формул методом Рунге-Кутта достаточно в формулах

(1) заменить

y

и

 

yxf ,

, коэффициенты

j

k

– на

 

4,3,2,1jk

j

.

Задание. Решить задачу Коши для системы дифференциальных уравнений

второго порядка, используя подпрограмму RGK. Результаты печатать на

каждом шаге.

Порядок выполнения лабораторной работы на ЭВМ.

1. Составить головную программу, содержащую обращение к RGK и печать

результатов на каждом шаге.

26

2. Составить подпрограмму вычисления правых частей P(X,Y,F).

3. Произвести вычисления на ЕС ЭВМ.

Варианты заданий.

На отрезке

 

3,0

с шагом

0,1

решить задачу Коши для системы

 





















.0

,00

.,,

,

202

1

21

2

1

yy

y

yyxf

dx

dy

y

dx

dy

№

варианта

 

21

,, yyxf

a

20

y

1

x

ae

6.0



0.01 0.5

2 0.02 1/3

3 0.03 0.25

4 0.04 0.2

5 0.05 1/6

6 0.06 1/7

7 0.07 0.125

8 0.08 1/9

9 0.09 0.1

10

12

yaxy 

0.06 1/7

11 0.07 0.125

12 0.08 1/9

13 0.09 0.1

14 0.1 1/11

15

x

ae



0.01 0.5

16 0.02 1/3

17 0.03 0.25

18 0.04 0.2

19 0.05 1/6

20

ax

e



 01.0

0.6 0.5

21 0.8 0.5

22 1.2 0.5

23

ax

e



 02.0

1.2 0.5

24

1

2

yxaxy 

0.14 1/15

25 0.15 1/16

26 0.16 1/17

27 0.17 1/18

28 0.18 1/19

29 0.19 0.05

30 0.2 1/21

Лабораторная работа № 10.

27

Решение задачи Дирихле для уравнения Пуассона

методом Чебышева

1. Постановка задачи

Явным методом Чебышева требуется найти приближённое решение

уравнения

 

21

2

1

2

, xxf

x

U

x

U









(1)

в квадрате

  

2,1,10:,:

21

 ixxxx

i

с краевыми условиями

0



U

, (2)

где



– граница квадрата



.

Выбираем функцию, удовлетворяющую краевым условиям (2)

  

2

22

2

11

xxxxU 

.

Вычислим

 

2

121

2

1

2

2 xxxx

x

U

x

U









.

Возьмём по определению в качестве правой части уравнения (1)

 

2

12121

2, xxxxxxf 

,

тогда нам известно точное решение

U

задачи (1), (2).

2. Теоретическая часть

От задачи (1), (2) перейдём к разностной. Вводим на плоскости

 

21

, xx

прямоугольную сетку с шагом

1

h

по направлению

1

x

и

2

h

по

направлению

2

x

. Получим

11

1 Nh 

,

22

1 Nh 

. Обозначим

 

2121

,...,1,0,,...,1,0,, NjNixxx

ji

ij



.

Обозначим через

h



множество внутренних узлов сетки, то есть



11

2

1





Nj

Ni

ijh

x



,

а через

h



– множество граничных узлов, то есть



11

,

11

0,

11

,

11

0

2

21

1





Nj

j

Ni

ih

xxxx

.

Пусть далее

hhh





1,1,11,1

1,2

,2

1,2







jjj

j

xxx

x







Рассмотрим конечномерное пространство функции

m

R

, заданных на

сетке

h



. Здесь

21

NNm 

и будем обозначать

 

jiji

xyy

,,



. Обозначим

2

,1,,1

,

2

1

,1,,1

,

2

,

2

2211

h

yyy

y

h

yyy

y

jijiji

jixx

jijiji

jixx











.

Тогда разностный оператор Лапласа записывается в виде

jixxjixx

ji

yyy

,,

,

2211



. (3)

28

Разностное выражение (3) называется пятиточечным разностным

шаблоном, так как содержит значения функции

 

21

, xxU

в пяти точках сетки, а

именно в точках

         

1

21

1

212

1

12

1

121

,,,,,,,,,

 jijijijiji

xxxxxxxxxx

(см. рис.).

Указанное множество точек называется шаблоном разностного оператора

Лапласа.

Заменим исходную задачу разностной задачей. При этом будем считать,

что

NNN 

21

, тогда

Nhhh 1

21



. Разностная аппроксимация задачи (1), (2),

принимает вид

hjijiji

xfy





,,,

,

, (4)

hjiji

xy 

,,

,0

или более подробно

ij

jijijijijiji

f

h

yyy

h

yyy











2

1,,1,

2

,1,,1

22

, (5)

1,...,2,1,,0,0

,,0,0,

 Njiyyyy

jNjNii

.

Обозначим через



пространство функций

y

, заданных на

h



и равных

нулю на границе

h



со скалярным произведением

 











1

,,

2

,

N

i

N

j

jiji

yhy



. (6)

В пространстве



определим оператор

 

jixxjixx

ji

yyy

,,

,

2211



. (7)

Тогда уравнение (5) можно записать в операторной форме

Fy 

, (8)

где

F

– функция, заданная на сетке

h



и

 

ijijji

fFxxF 

21

,

. Сеточные функции

y

и

F

будем рассматривать как вектора

 

2

1N 

– мерного пространства



с

координатами

ji

y

,

.

Наименьшее и наибольшее собственные значения оператора



равны

2

sin

8

2

min





h



,

(9)

2

cos

8

2

max





h



.

3. Метод решения

Разностную задачу (5) будем решать явным итерационным методом с

чебышевским набором параметров, который выражается следующей

формулой:

 

k

kk

yfTyy 

1

, (10)

где

nk ,...,1

,

n

-заданное число итераций,

 

minmax

min

0

,

2

,

2

12

cos,

1























 pT

n

k

t

pt

T

msx

k

. (11)

4. Алгоритм

29

1) Задаём количество итераций, например,

10n 

, полагаем

10N

, тогда

шаг сетки

Nh 1

=0,1.

2) По формулам (9), (11) вычисляем

2

0

4

h

T 

,

2

1

2

h

p tg



 

.

3) Вычисляем

k



и

k

t

по формулам (11).

4) Полагая

0

0y 

по формуле (10) находим

10

y

.

5) Этап 4 повторяем, полагая

0 10

.y y

6) Итерационный процесс продолжаем до совпадения первых четырех

знаков в последних итерациях по циклам.

5. Оформление результатов работы.

Результаты вычислений представить в виде трех таблиц: две последние

итерации и значения точного решения на сетке.

30

Голичев И.И. Лабораторный практикум по курсу «Численные методы»

Подождите немного. Документ загружается.