Глазов А.И., Морозов М.В. (сост.) Геометрическая кристаллография

Подождите немного. Документ загружается.

Министерство образования РФ

Санкт-Петербургский государственный горный институт имени Г.В.Плеханова

(технический университет)

Кафедра минералогии, кристаллографии и петрографии

ГЕОМЕТРИЧЕСКАЯ

КРИСТАЛЛОГРАФИЯ

Методические указания к лабораторным работам по

дисциплине «Кристаллография» для студентов

специальностей 080600 и 080100

Санкт-Петербург

2000

УДК 548.0

Геометрическая кристаллография: Методические указания к

лабораторным работам по дисциплине «Кристаллография» для студентов

специальностей 080600 и 080100 / Санкт-Петербургский горный институт;

Составители: А.И.Глазов, М.В.Морозов. СПб, 2000. 41 с.

Методические указания содержат описания и рекомендации по выполнению

лабораторных работ по дисциплине «Кристаллография». В приложении приводится

краткий англо-русский словарь основных терминов и образцы оформления отчетов.

Методические указания предназначены для студентов специальностей 080600

«Прикладная геохимия, минералогия и петрология» и 080100 «Геологическая

съемка и поиски месторождений полезных ископаемых».

Научный редактор проф. Ю.Б. Марин.

институт им. Г.В. Плеханова, 2000 г.

ВВЕДЕНИЕ

Студенты специальностей 080600 «Прикладная геохимия,

минералогия и петрология» и 080100 «Геологическая съемка и

поиски месторождений полезных ископаемых» выполняют

лабораторные работы по кристаллографии на первом курсе в

весеннем (втором) семестре. Геометрическая кристаллография

является базовым разделом минералогической кристаллографии и

традиционно входит в число приоритетных направлений

деятельности ученых Санкт-Петербургского горного института.

Графическое представление результатов измерения

кристаллов

минералов (стереографические проекции граней, чертежи

минеральных индивидов и их срастаний) является наиболее

информативным способом характеристики их габитуса,

взаимоотношения кристаллов в агрегатах и широко используется

при решении задач теоретической и прикладной минералогии.

Квалификация «инженер-геолог» предполагает умение

анализировать и использовать результаты морфологического

исследования кристаллов при изучении генетических

закономерностей формирования минеральных

месторождений,

решении вопросов типоморфизма минералов, для технологической и

геммологической характеристик кристаллов.

Эффективно решать названные задачи на современном уровне

позволяет широкое применение компьютеров и

специализированного программного обеспечения, обучение работе с

которыми происходит в рамках лабораторных занятий по

дисциплине «Кристаллография».

Выполнение лабораторных работ преследует следующие цели:

1) закрепление и углубление теоретических знаний, полученных

при прохождении учебного курса;

2) приобретение опыта самостоятельной практической

обработки результатов измерения кристаллов минералов,

характеристики их габитуса;

3) развитие навыков использования современного

программного обеспечения при решении задач кристаллографии,

минералогии, петрографии и минералогического материаловедения.

Лабораторные работы выполняются в индивидуальном порядке.

1. СТЕРЕОГРАФИЧЕСКИЕ ПРОЕКЦИИ

Одним из первых достижений кристаллографии стало открытие

закона постоянства углов (закона Стено – Ломоносова – Ромэ-

Делиля), который гласит, что во всех кристаллах, принадлежащих

одной полиморфной модификации данного вещества, при

одинаковых условиях, углы между соответственными гранями (и

ребрами) постоянны. С тех пор измерение кристаллов стало одним

из важнейших направлений развития кристаллографии, которое

позволило производить точную диагностику многих минералов и

синтетических веществ и изучать закономерности изменчивости

облика кристаллов в природе.

Измерения кристаллов проводят на оптических гониометрах.

Различают два типа гониметров – однокружные, позволяющие

определять углы между парами граней, и двукружные, позволяющие

определять сферические координаты граней.

Наиболее удобным способом представления численных

результатов гониометрии является графическое изображение

элементов огранения кристалла (а также элементов его симметрии)

на стереографических проекциях (от греч. стереос –

пространственный). Подробно теория построения

стереографических проекций излагается в учебниках по

кристаллографии.

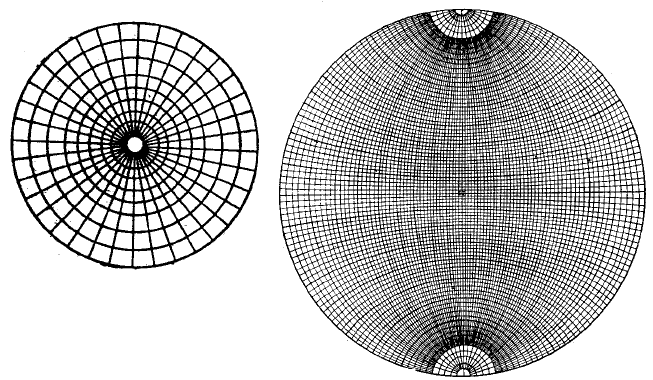
Для удобства построения проекций используются специальные

стереографические сетки (например, «сетка Болдырева», рис. 1),

наибольшее распространение из которых получила в

кристаллографии сетка Вульфа (рис. 2), предложенная русским

ученым

Г.В. Вульфом в 1897 году. Она представляет собой

стереографическую проекцию градусной сети сферы на

меридиональную плоскость. Стандартный радиус сетки – 100 мм,

цена деления – 2°. Работа ведётся не на самой сетке, а на кальке.

Следует помнить, что точка с ρ = 0° обычно помещается в центре

сетки. Через него проходят два диаметра – проекции больших

кругов сферы

, перпендикулярных плоскости проекции. Мы можем

принять их за вспомогательные меридианы, и измерение и

откладывание углов ρ производится от центра только вдоль этих

диаметров. Большинство задач геометрической кристаллографии

могут быть решены с необходимой точностью посредством сетки

Вульфа вручную; ниже приведены примеры, иллюстрирующие

общие приемы их решения. Для проведения высокоточных работ

рекомендуется использовать специализированное программное

обеспечение, обзор которого проводится во втором разделе

указаний.

Лабораторная работа по использованию сетки Вульфа

выполняется в рамках домашнего задания №

1 по дисциплине

«Кристаллография».

Рис. 1. Рис. 2.

Принципы решения задач на сетке Вульфа

1. По заданным (ϕ; ρ) построить проекцию заданного

направления.

Решение. По внешнему кругу отсчитываем от отметки нулевого

меридиана по часовой стрелке значение данного ϕ и отмечаем его

радиальной чёрточкой. Вращая кальку вокруг центра сетки,

приводим эту отметку на ближайший диаметр и, отсчитав по нему

от центра сетки данное ρ, отмечаем полученную точку и обводим её

кружком. Если ρ>90°, то, дойдя до края сетки, отсчитываем по тому

же диаметру к центру недостающий угол ρ–90°. Эти точки нижней

полусферы, в отличие от верхних, обозначаем крестиками. Обратная

задача (по проекции данного направления найти его сферические

координаты) решается

в обратном порядке.

2. Измерить угол между двумя направлениями, заданными их

стереографическими проекциями (т. е. угол между двумя точками на

проекции).

Решение. На сфере все расстояния – и линейные, и угловые –

измеряются по дугам больших кругов. На сетке Вульфа есть

достаточно широкий набор проекций больших кругов: это,

очевидно, линии меридианов. Вращая кальку

, добиваемся, чтобы

заданные точки оказались на одном меридиане. По нему

отсчитывается искомый угол. Если одна из точек лежит в верхней

полусфере, а другая – в нижней, следует использовать меридианы,

равно отстоящие влево и вправо от вертикального диаметра. Их

можно рассматривать как проекцию одного большого круга, одна

половина которого пересекает верхнюю полусферу,

другая –

нижнюю.

3. Найти проекцию P полюса данного большого круга. Смысл

этой задачи может состоять, например, в том, чтобы по заданной

стереографической проекции некоторой плоскости кристалла

построить её гномостереографическую проекцию, или по

гномостереографическим проекциям граней одной зоны найти

стереографическую проекцию оси этой зоны (поскольку нормали к

граням одной зоны лежат в

одной плоскости, их проекции лежат на

одной дуге большого круга).

Решение. На сетке есть проекция большого круга,

перпендикулярного к любой из меридиональных плоскостей, это –

горизонтальный диаметр сетки. Поэтому, приведя вращением

кальки данную дугу большого круга на один из меридианов,

отсчитываем от него по горизонтальному диаметру в сторону центра

сетки 90°. Это и

будет искомая проекция Р. Обратная задача

решается в обратном порядке.

Задание к лабораторной работе 1

Требуется построить гномостереографическую проекцию всех

граней кристалла и стереографическую проекцию избранных ребер,

а также определить углы между заданными гранями по следующим

данным:

¾ вид (класс) симметрии;

¾ сферические координаты граней (углы ϕ и ρ) или углы между

гранями.

Порядок выполнения работы

Положим перед собой сетку Вульфа так, как это показано на

рис. 2. В дальнейшем будем иметь в виду, что никакие построения

на самой сетке не производятся – задачи целиком решаются на

листке кальки или восковки, наложенном на сетку.

Чтобы иметь возможность всегда приводить кальку

относительно сетки в одно и то же исходное

положение, отмечаем

на кальке центр сетки точкой с четырьмя черточками в виде креста,

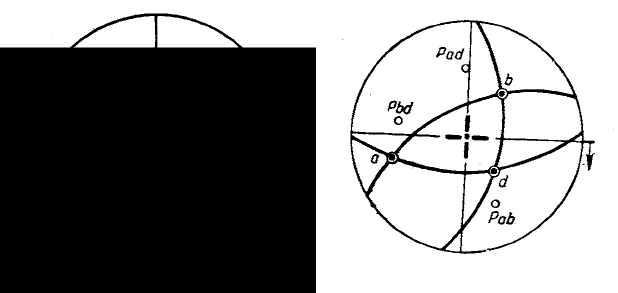
не доходящими до самой точки. Кроме того, у правого конца

горизонтального диаметра сетки ставится небольшая черточка,

проведенная вне круга проекций (рис. 3).

Черточка справа будет служить нулевым индексом для долгот

0° ϕ (полезно надписать это значение), а центральная

точка рисунка

– местом нуля для полярных расстояний 0° ρ.

Первая сферическая координата – долгота ϕ – отсчитывается по

кругу проекций от нулевого индекса по часовой стрелке (на сетке

каждое деление соответствует 2°, каждый десятый градус выделен

жирной линией).

Вторая сферическая координата – полярное расстояние ρ –

отсчитывается от центра сетки.

Напомним, что в дальнейшем изображенные

на сетке дуги

меридианов и параллелей будут служить лишь вспомогательными

линиями. Истинный полюс сетки находится в ее центре (0° ρ),

истинный экватор совпадает с кругом проекций, а из истинных

меридианов на сетке изображены только два – вертикальный и

горизонтальный диаметры сетки.

При работе с сеткой Вульфа мы должны всегда мысленно

представлять себе совмещенную с ней простейшую

стереографическую сетку (рис. 1). Само собой разумеется, что

отсчет полярных расстояний ρ должен производиться при этом от

центра сетки, как от полюса.

Рис. 3. Рис. 4.

Задача 1. Построить стереографическую проекцию

направления, заданного сферическими координатами ϕ и ρ.

Например, пусть некоторое направление А задано

сферическими координатами ϕ=165° и ρ=68°: А (165°, 68°).

Требуется найти стереографическую проекцию этого направления.

1. Накладываем кальку на сетку и ставим на ней центральный

крестик и черточку нулевого индекса для ϕ (рис. 3);

2. От нулевого

индекса для ϕ по кругу проекций (по часовой

стрелке) отсчитываем первую сферическую координату – долготу ϕ

(165°) и отмечаем результат на внешнем круге вспомогательной

чертой;

3. Вращением кальки (центр кальки при этом всегда должен

совпадать с центром сетки) совмещаем найденную вспомогательную

черту с концом ближайшего диаметра сетки;

4. По этому диаметру от центра сетки в сторону

вспомогательной черты отсчитываем вторую сферическую

координату – полярное расстояние ρ (68°) – и отмечаем найденную

точку небольшим кружком;

5. Возвращаем кальку в исходное положение и надписываем

точку а.

Точка а является искомой стереографической проекцией

направления А.

В кристаллографии эта задача обычно применяется при

решении следующих вопросов

1. Даны сферические координаты нормали к грани кристалла;

требуется найти стереографическую проекцию нормали к грани,

или, что то же самое, гномостереографическую проекцию самой

грани.

2. Даны сферические координаты ребра кристалла или какого-

нибудь его характерного направления (например, оси симметрии);

требуется построить стереографическую проекцию этого ребра (или

направления).

Предлагаем самостоятельно изобразить стереографические

проекции следующих направлений: В (309°, 55°), D (51°, 37°), Е

(122°, 90°) и Н (205°, 124°)

Задача 2 (обратная). Определить сферические координаты

направления, заданного стереографической проекцией.

1. Вращением кальки приводим заданную точку

(стереографическую проекцию направления) на ближайший диаметр

сетки. По этому диаметру от центра сетки до заданной точки

отсчитываем сферическую координату ρ и отмечаем

вспомогательной чертой на круге

проекций тот конец упомянутого

диаметра, в направлении которого лежит наша точка (рис.

3).

2. По кругу проекций отсчитываем сферическую координату

ϕ: от нулевого индекса по часовой стрелке до вспомогательной

черточки.

Задача 3. Провести дугу большого круга через заданные

стереографические проекции двух направлений.

Например, провести дугу большого круга через

стереографические проекции а и b направлений А (165°, 68°) и

В (309°, 55°).

1. Вращением кальки добиваемся того, чтобы обе заданные

точки a и b оказались на одной из вспомогательных

меридиональных дуг сетки Вульфа.

2. Найденную дугу тщательно

обводим карандашом и

возвращаем кальку в исходное положение (рис. 4).

Если заданные точки изображают гномостереографические

проекции граней, то найденная дуга большого круга представляет

гномостереографическую проекцию ребра между обеими гранями,

(для получения гномостереографической проекции ребра последнее

заменяем плоскостью, к нему перпендикулярной, и находим

стереографическую проекцию этой плоскости).

Если заданные точки изображают стереографические

проекции

ребер, то найденная дуга большого круга является

стереографической проекцией грани, в плоскости которой лежат

упомянутые ребра.

Предлагаем провести на кальке также дуги bd и ad через

заданные выше точки.

Задача 4. Измерить угол между двумя направлениями,

заданными их стереографическими проекциями (например, угол

между направлениями А и В).

1. Как и при

решении предыдущей задачи, вращением кальки

совмещаем данные точки а и b с одной из меридиональных дуг

сетки Вульфа (задача 3).

2. Отсчитываем по этой меридиональной дуге количество

градусов, заключенных между точками а и b (рис. 4). В результате

получаем ∠AB=113°.

Примечание. Аналогично можно найти, что ∠AD=86°, а

∠BD=70°.

Если заданные

точки представляют собой

гномостереографические проекции граней, то измеренный угол

является углом между нормалями к этим граням.