Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

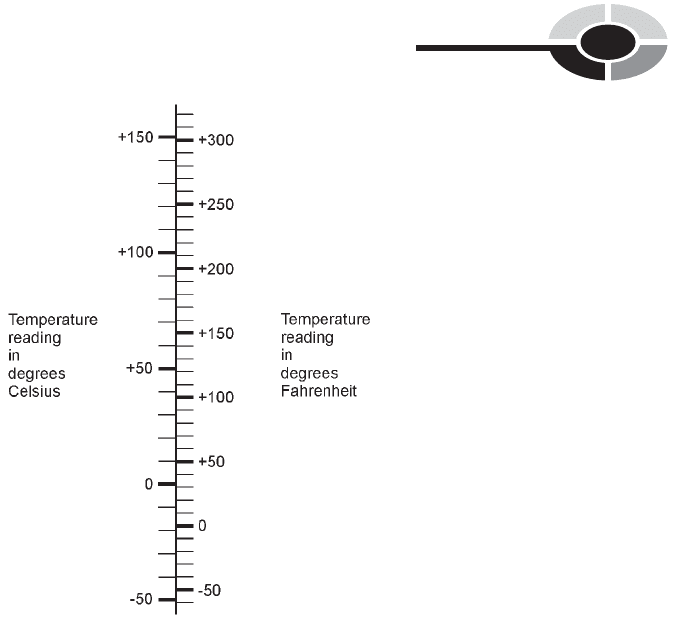
magnitude of a speciﬁc quantity must be compared according to two diﬀerent

unit scales. In Fig. 2-7, a nomograph compares temperature readings in

degrees Celsius (also called centigrade) and degrees Fahrenheit.

POINT-TO-POINT GRAPHS

In a point-to-point graph, the scales are similar to those used in continuous-

curve graphs such as Figs. 2-2 and 2-3. But the values of the function in

a point-to-point graph are shown only for a few selected points, which are

connected by straight lines.

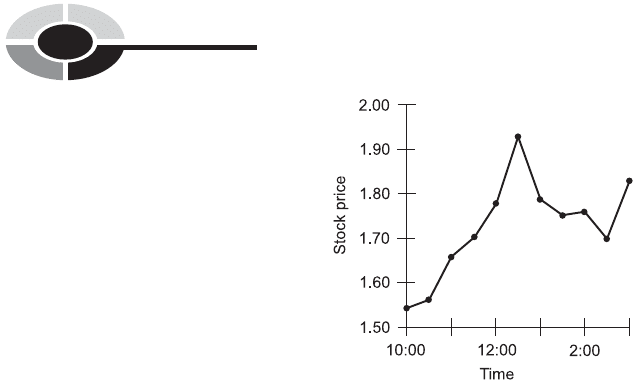
In the point-to-point graph of Fig. 2-8, the price of Stock Y (from Fig. 2-2)

is plotted on the half-hour from 10:00 A.M. to 3:00 P.M. The resulting

‘‘curve’’ does not exactly show the stock prices at the in-between times.

But overall, the graph is a fair representation of the ﬂuctuation of the stock

over time.

When plotting a point-to-point graph, a certain minimum number of

points must be plotted, and they must all be suﬃciently close together. If a

Fig. 2-7. An example of a nomograph for converting temperature readings.

CHAPTER 2 How Variables Relate 41

point-to-point graph showed the price of Stock Y at hourly intervals, it would

not come as close as Fig. 2-8 to representing the actual moment-to-moment

stock-price function. If a point-to-point graph showed the price at 15-minute

intervals, it would come closer than Fig. 2-8 to the moment-to-moment

stock-price function.

CHOOSING SCALES

When composing a graph, it’s important to choose sensible scales for

the dependent and independent variables. If either scale spans a range of

values much greater than necessary, the resolution (detail) of the graph will

be poor. If either scale does not have a large enough span, there won’t

be enough room to show the entire function; some of the values will be

‘‘cut oﬀ.’’

PROBLEM 2-3

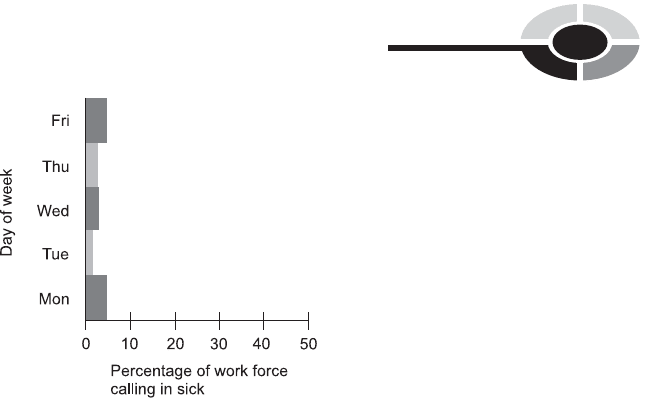
Figure 2-9 is a hypothetical bar graph showing the percentage of the work

force in a certain city that calls in sick on each day during a particular

work week. What, if anything, is wrong with this graph?

SOLUTION 2-3

The dependent-variable scale is too large. It would be better if the horizontal

scale showed values only in the range of 0 to 10%. The graph could also be

improved by listing percentage numbers at the right-hand side of each bar.

Another way to improve the graph would be to put the independent variable

on the horizontal axis and the dependent variable on the vertical axis, making

the graph a vertical bar graph instead of a horizontal bar graph.

Fig. 2-8. A point-to-point graph of hypothetical stock price versus time.

PART 1 Expressing Quantities

PROBLEM 2-4

What’s going on with the percentage values depicted in Fig. 2-9? It is

apparent that the values don’t add up to 100%. Shouldn’t they?

SOLUTION 2-4

No. If they did, it would be a coincidence (and a bad reﬂection on the attitude

of the work force in that city during that week). This is a situation in

which the sum of the percentages in a bar graph does not have to be

100%. If everybody showed up for work every day for the whole week, the

sum of the percentages would be 0, and Fig. 2-9 would be perfectly legitimate

showing no bars at all.

Tweaks, Trends, and Correlation

Graphs can be approximated or modiﬁed by ‘‘tweaking.’’ Certain charac-

teristics can also be noted, such as trends and correlation. Here are a few

examples.

LINEAR INTERPOLATION

The term interpolate means ‘‘to put between.’’ When a graph is incomplete,

estimated data can be put in the gap(s) in order to make the graph

look complete. An example is shown in Fig. 2-10. This is a graph of the

price of the hypothetical Stock Y from Fig. 2-2, but there’s a gap during

Fig. 2-9. Illustration for Problems 2-3 and 2-4.

CHAPTER 2 How Variables Relate 43

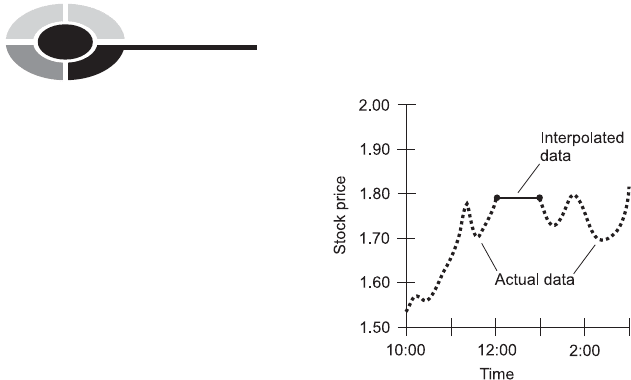
the noon hour. We don’t know exactly what happened to the stock price

during that hour, but we can ﬁll in the graph using linear interpolation.

A straight line is placed between the end points of the gap, and then the

graph looks complete.

Linear interpolation almost always produces a somewhat inaccurate

result. But sometimes it is better to have an approximation than to have no

data at all. Compare Fig. 2-10 with Fig. 2-2, and you can see that the linear

interpolation error is considerable in this case.

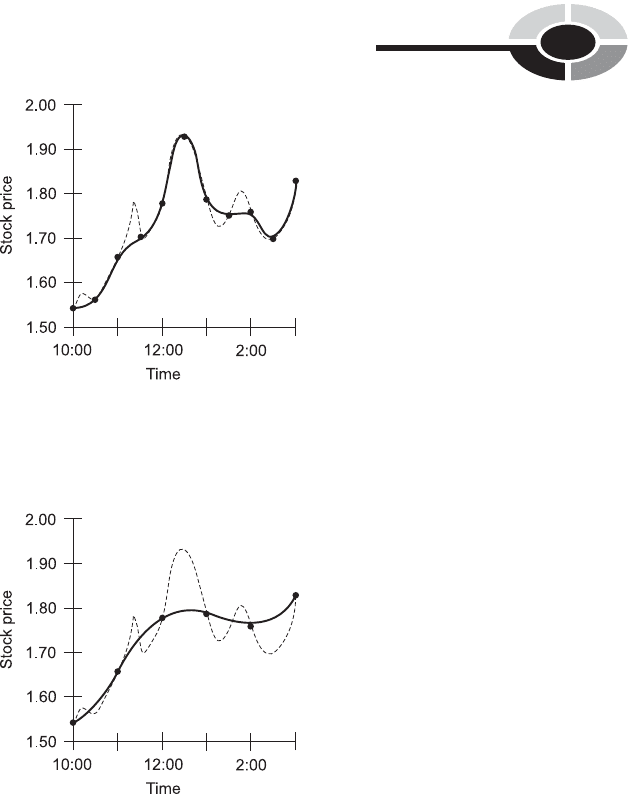
CURVE FITTING

Curve ﬁtting is an intuitive scheme for approximating a point-to-point graph,

or ﬁlling in a graph containing one or more gaps, to make it look like a

continuous curve. Figure 2-11 is an approximate graph of the price of

hypothetical Stock Y, based on points determined at intervals of half an

hour, as generated by curve ﬁtting. This does not precisely represent the

actual curve of Fig. 2-2, but it comes close most of the time.

Curve ﬁtting becomes increasingly accurate as the values are determined

at more and more frequent intervals. When the values are determined

infrequently, this scheme can be subject to large errors, as is shown by the

example of Fig. 2-12.

EXTRAPOLATION

The term extrapolate means ‘‘to put outside of.’’ When a function has a

continuous-curve graph where time is the independent variable, extrapolation

Fig. 2-10. An example of linear interpolation. The thin solid line represents the interpolation

of the values for the gap in the actual available data (heavy dashed curve).

PART 1 Expressing Quantities

is the same thing as short-term forecasting. Two examples are shown in

Fig. 2-13.

In Fig. 2-13A, the price of the hypothetical Stock X from Fig. 2-2 is

plotted until 2:00 P.M., and then an attempt is made to forecast its price for

an hour into the future, based on its past performance. In this case, linear

extrapolation, the simplest form, is used. The curve is simply projected ahead

as a straight line. Compare this graph with Fig. 2-2. In this case, linear

extrapolation works fairly well.

Figure 2-13B shows the price of the hypothetical Stock Y (from Fig. 2-2)

plotted until 2:00 P.M., and then linear extrapolation is used in an attempt to

Fig. 2-11. Approximation of hypothetical stock price as a continuous function of time,

making use of curve ﬁtting. The solid curve represents the approximation; the dashed curve

represents the actual price as a function of time.

Fig. 2-12. An example of curve ﬁtting in which not enough data samples are taken, causing

signiﬁcant errors. The solid line represents the approximation; the dashed curve represents the

actual price as a function of time.

CHAPTER 2 How Variables Relate 45

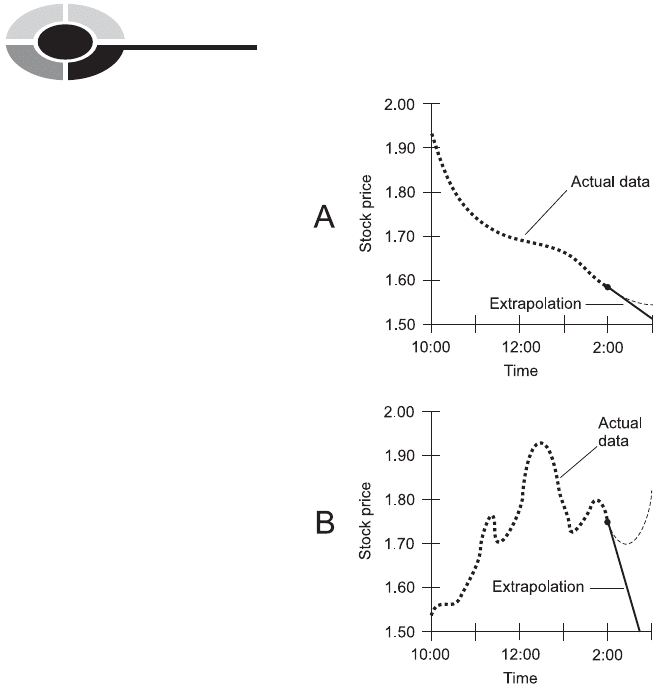
predict its behavior for the next hour. As you can see by comparing this

graph with Fig. 2-2, linear extrapolation does not work well in this scenario.

Extrapolation is best done by computers. Machines can notice subtle

characteristics of functions that humans miss. Some graphs are easy to

extrapolate, and others are not. In general, as a curve becomes more

complicated, extrapolation becomes subject to more error. Also, as the extent

(or distance) of the extrapolation increases for a given curve, the accuracy

decreases.

TRENDS

A function is said to be nonincreasing if the value of the dependent variable

never grows any larger (or more positive) as the value of the independent

Fig. 2-13. Examples of linear extrapolation. The solid lines represent the forecasts; the

dashed curves represent the actual data. In the case shown at A, the prediction is fairly

good. In the case shown at B, the linear extrapolation is way oﬀ.

PART 1 Expressing Quantities

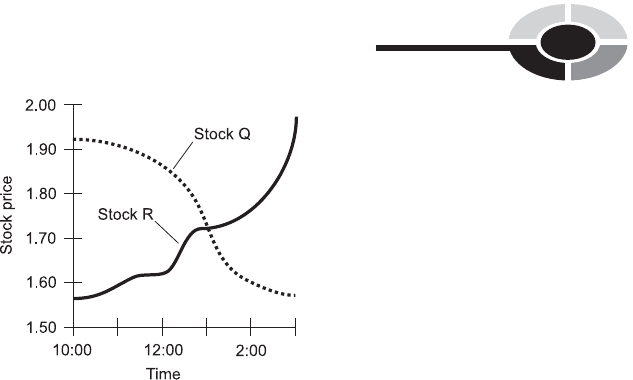
variable increases. If the dependent variable in a function never gets any

smaller (or more negative) as the value of the independent variable increases,

the function is said to be nondecreasing.

The dashed curve in Fig. 2-14 shows the behavior of a hypothetical

Stock Q, whose price never rises throughout the period under consideration.

This function is nonincreasing. The solid curve shows a hypothetical

Stock R, whose price never falls throughout the period. This function is

nondecreasing.

Sometimes the terms trending downward and trending upward are used

to describe graphs. These terms are subjective; diﬀerent people might

interpret them diﬀerently. Everyone would agree that Stock Q in Fig. 2-14

trends downward while Stock R trends upward. But a stock that rises

and falls several times during a period might be harder to deﬁne in this

respect.

CORRELATION

Graphs can show the extent of correlation between the values of two variables

when the values are obtained from a ﬁnite number of experimental samples.

If, as the value of one variable generally increases, the value of the

other generally increases too, the correlation is considered positive.

If the opposite is true – the value of one variable increases as the other

generally decreases – the correlation is considered negative. If the points

are randomly scattered all over the graph, then the correlation is considered

to be zero.

Fig. 2-14. The price of Stock Q is nonincreasing versus time, and the price of Stock R is

nondecreasing versus time.

CHAPTER 2 How Variables Relate 47

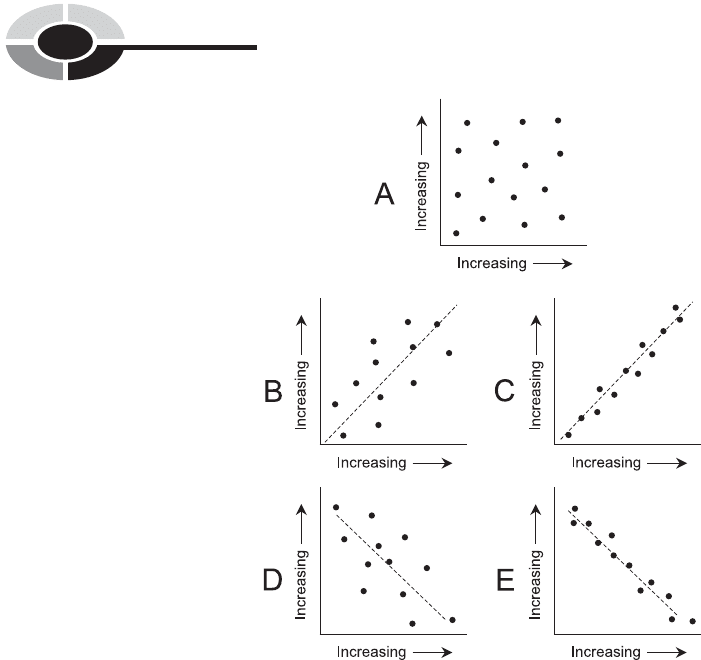
Figure 2-15 shows ﬁve examples of point sets. At A the correlation is zero.

At B and C, the correlation is positive. At D and E, the correlation is

negative.

PROBLEM 2-5

Suppose, as the value of the independent variable in a function changes, the

value of the dependent variable does not change. This is called a constant

function. Is its graph nonincreasing or nondecreasing?

SOLUTION 2-5

According to our deﬁnitions, the graph of a constant function is both non-

increasing and nondecreasing. Its value never increases, and it never

decreases.

PROBLEM 2-6

Is there any type of function for which linear interpolation is perfectly

accurate, that is, ‘‘ﬁlls in the gap’’ with zero error?

Fig. 2-15. Point plots showing zero correlation (A), weak positive correlation (B), strong

positive correlation (C), weak negative correlation (D), and strong negative correlation (E).

PART 1 Expressing Quantities

SOLUTION 2-6

Yes. If the graph of a function is known to be a straight line, then linear inter-

polation can be used to ‘‘ﬁll in a gap’’ and the result will be free of error.

An example is the speed of a car that accelerates at a known, constant

rate. If its speed-versus-time graph appears as a perfectly straight line with

a small gap, then linear interpolation can be used to determine the car’s

speed at points inside the gap, as shown in Fig. 2-16. In this graph, the

heavy dashed line represents actual measured data, and the thinner solid

line represents interpolated data.

Quiz

Refer to the text in this chapter if necessary. A good score is eight correct.

Answers are in the back of the book.

1. Suppose a graph is drawn showing temperature in degrees Celsius (8C)

as a function of time for a 24-hour day. The temperature measure-

ments are accurate to within 0.1 8C, and the readings are taken

every 15 minutes. The day’s highest temperature is þ23.8 8C at 3:45

P.M. The day’s lowest temperature is þ13.5 8C at 5:30 A.M. A reason-

able range for the temperature scale in this graph is

(a) 0.0 8Ctoþ100.0 8C

(b) 100.0 8Ctoþ100.0 8C

(d) þ10.0 8Ctoþ30.0 8C

Fig. 2-16. Illustration for Problem 2-6.

CHAPTER 2 How Variables Relate 49

2. In a constant function:

(a) the value of the dependent variable constantly increases as the

value of the independent variable increases

(b) the value of the dependent variable constantly decreases as the

value of the independent variable increases

(d) the value of the dependent variable does not change

3. In Fig. 2-17, which of the curves represents y as a function of x?

(a) Curve A only.

(b) Curve B only.

(d) Neither curve A nor curve B.

4. In Fig. 2-17, which of the curves represents x as a function of y?

(a) Curve A only.

(b) Curve B only.

(d) Neither curve A nor curve B.

5. In Fig. 2-17, which of the curves represents a relation between x and y?

(a) Curve A only.

(b) Curve B only.

(d) Neither curve A nor curve B.

Fig. 2-17. Illustration for Quiz Questions 3 through 6.

PART 1 Expressing Quantities