Geiser J. Decomposition Methods for Differential Equations: Theory and Applications

Подождите немного. Документ загружается.

Chapter 1

Modeling: Multi-Physics Problems

1.1 Introduction

In this chapter we introduce our monograph and the related mathematical

theory and applications.

In various applications in the material physics, geoscience, and chemical

engineering, the simulations of multi-physics problems are very important.

A multi-physics problem is deﬁned as a problem with diﬀerent physical

processes, dependent in time and space (e.g., ﬂow-process, reaction-process,

growth-process, etc.).

Because of the large diﬀerential equation systems, an enormous increase

in performance for the simulation programs is necessary and high complex

algorithms are needed for fast computations.

The mathematical models of the multi-physics problems consist usually of

coupled partial diﬀerential equations. They reﬂect the underlying physical be-

havior of the processes. The most relevant problems are no longer analytically

solvable and so numerical solutions are necessary.

Based on the physical behavior, the numerical methods are developed in

such a manner that the physical laws are conserved.

We will concentrate on the multi-physics problems based on linear and non-

linear coupled parabolic and hyperbolic equation systems. Thus, the coupled

equation systems have at least parabolic characteristics.

The questions in this monograph are how to decouple the equations to

conserve the physical behavior and how to accelerate the solver process for

simpler equations and how to achieve higher-order methods for more accurate

computations.

In the next sections we discuss the multi-physics problems.

1.2 Models for Multi-Physics Problems

We will concentrate on a family of multi-physics problems related to ﬂow

and reaction problems, where we separate the ﬂow problems into convection,

6Decomposition Methods for Diﬀerential Equations Theory and Applications

diﬀusion and wave-propagation problems, see [23], [24], [41], [60], [61] and

[66].

The underlying model is funded in applications for transport reaction, heat,

and ﬂow processes in geophysics, material sciences, quantum physics, and

more.

The problem can be discussed for weak- and strong-coupled equations, thus

for each physical process we can concentrate on simpler model equations that

are suﬃcient for analyzing the multi-physics problems.

1.3 Examples for Multi-Physics Problems

The next problems are selected to apply our decomposition methods and

to discuss the inﬂuence of the development of the splitting ideas, see [193].

1.3.1 Waste Disposal

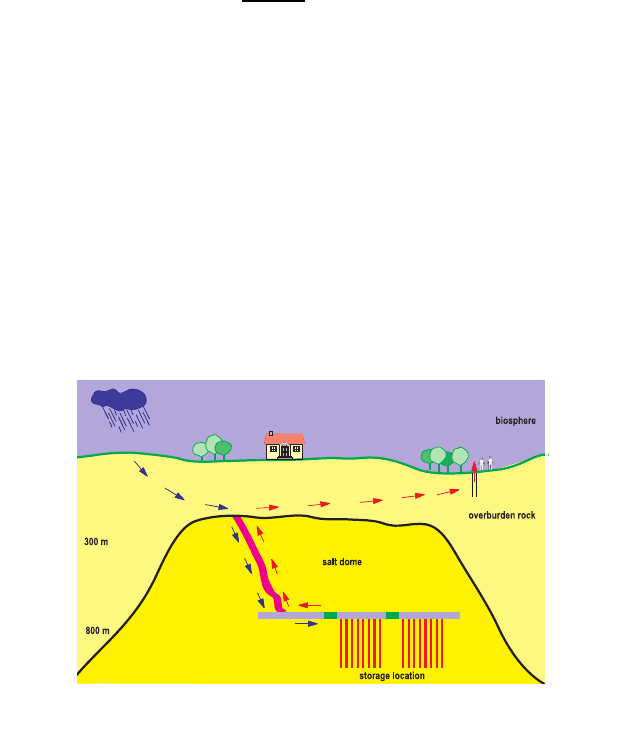
We simulate a waste disposal for radioactive waste in a salt dome. The salt

dome is surrounded by a spacious, heterogenous overlaying rock (a schematical

overview is presented in Figure 1.1).

For a potential waste case, groundwater spools in the possible pathway inside

the waste disposal and contacts with radioactive waste.

Because of the high pressures and motions in the salt dome, the overlaying

rock presses out the contaminant water for the salt dome. The contaminant

water is then used as a time-dependent source for the radionuclides in the

groundwater ﬂow.

The radionuclides are transported via the groundwater and we neglect the

pressed out water mass compared with the water of the groundwater ﬂow. For

the reactive processes, we use the radioactive decay that denotes the transfer

from a radionuclide in the corresponding child nuclide and the adsorption that

denotes the exchange in the several abidance areas for the mobile or immobile

phase, cf. [81].

The modeling for these cases is done in [24], [47], [135], and [73]. Based on

the physical model, we could derive the mathematical models.

We describe for simpliﬁcation a model for equilibrium sorption. This model

is studied in various directions and we explain the model in [81]. The phases

for the contaminants are presented in the mobile, immobile, sorption, and

immobile sorption phase, cf. [81].

Modeling: Multi-Physics Problems 7

The model equations are given as

φ∂

+ ∇·(vc

− D∇c

)=−φR



k=k(i)

φR

,(1.1)

e(i)



=1+

(1 − φ)

ρK(c

e(i)

), with i =1,...,M,

where c

is the i-th concentration, R

is the i-th retardation factor, λ

the i-th

decay constant, and v the velocity ﬁeld that is computed by another program

package (e.g., d

f-program package, see [72]) or that is given a priori. Q

is the

i-th source-term, φ is the porosity, c

e(i)

is the sum of all isotopic concentrations

of the element e, K is a function of the isotherms, see [81]. M is the number

of the radioactive concentrations.

Figure 1.1 presents the physical circumstances of a waste disposal as given

in the task.

FIGURE 1.1: Schematical overview of the waste disposal, cf. [32]

REMARK 1.1 For this model the splitting methods are applied with

respect to decouple the fast reaction processes and the slow transport pro-

cesses. We can apply fast ordinary diﬀerential equation (ODE) solvers for the

8Decomposition Methods for Diﬀerential Equations Theory and Applications

reaction processes and implicit partial diﬀerential equation (PDE) solvers for

the transport processes, see [124].

1.3.2 Crystal Growth

The motivation for modeling an accurate technical apparatus or physical

process is coming from the demand to have a tool for developing an optimal

and eﬃcient apparatus for foreseeing the physical eﬀects and protecting the

environment.

The basic idea for the model is the transfer between reality and the possible

abstraction for an implementable model. Often some interested eﬀects are

suﬃcient to develop a simpler model from the reality.

Silicon carbide (SiC) is a wide-bandgap semiconductor used in high-power

and high-frequency industrial applications: SiC serves as substrate material

for electronic and optoelectronic devices such as MOSFETs, thyristors, blue

lasers, and sensors (see [152] for a recent account of advances in SiC devices).

Its chemical and thermal stability make SiC an attractive material to be used

in high temperature applications as well as in intensive radiation environ-

ments. For an economically viable industrial use of SiC, growth techniques

for large diameter, low defect SiC boules must be available. Recent years

have seen steady improvement (see [122]) of size and quality of SiC single

crystals grown by sublimation via physical vapor transport (PVT, also known

as modiﬁed Lely method, see, e.g., [140]). However, many problems remain,

warranting further research.

Typically, modern PVT growth systems consist of an induction-heated

graphite crucible containing polycrystalline SiC source powder and a single

crystalline SiC seed (see Figure 6.19). The source powder is placed in the hot

zone of the growth apparatus, whereas the seed crystaliscooledbymeansofa

blind hole, establishing a temperature diﬀerence between source and seed. As

the SiC source is kept at a higher temperature than the cooled SiC seed, sub-

limation is encouraged at the source and crystallization is encouraged at the

seed, causing the partial pressures of Si, Si

C,andSiC

to be higher in the

neighborhood of the source and lower in the neighborhood of the seed. As the

system tries to equalize the partial pressures, source material is transported

to the seed which grows into the reaction chamber.

Because of the complex processes, a careful study is important to correctly

design the numerical simulations, [165]. Based on this background the combi-

nation of discretization and solver methods is an important task. We propose

the decomposition methods of breaking down complicated multi-physics in

simpler physics. The time-decomposition methods and their extended ver-

sions with more stabilized behavior are based on operator-splitting methods,

see [70]. With these methods a useful decoupling of the time scales is possi-

ble, and the solvers can be applied on the diﬀerent time scales. Further, the

space-decomposition methods are based on the Schwarz waveform-relaxation

methods and their accurate error estimates, see [54]. The methods decouple

Modeling: Multi-Physics Problems 9

into domains with the same equation parameters, therefore eﬀective spatial

discretization and solver methods are applicable.

The model is given as follows:

a) We assume that the temperature evolution inside the gas region Ω

can

be approximated by considering the gas as pure argon. The reduced heat

equation is given as

∂

−∇·(κ

∇T )=0, (1.2)

= z

T, (1.3)

where T is the temperature, t is the time, and U

is the internal energy of the

argon gas. The parameters are given as ρ

being the density of the argon gas,

being the thermal conductivity, z

being the conﬁguration number, and

being the gas constant for argon.

b) The temperature evolution inside the region of solid materials Ω

(e.g., in-

side the silicon carbide crystal, silicon carbide powder, graphite, and graphite

insulation), is described by the heat equation:

∂

−∇·(κ

∇T )=f, (1.4)



(S) dS, (1.5)

where ρ

is the density of the solid material, U

is the internal energy, κ

the thermal conductivity, and c

is the speciﬁc heat. f represents the heat

source in the material Ω

The equations hold in the domains of the respective materials and are cou-

pled by interface conditions, for example, those requiring the continuity for

the temperature and for the normal components of the heat ﬂux on the in-

terfaces between opaque solid materials. On the boundary of the gas domain

(i.e., on the interface between the solid material and the gas domain), we

consider the interface condition

∇T · n

+ R − J = κ

∇T · n

, (1.6)

where n

is the normal vector of the gas domain, R is the radiosity, and J

is the irradiosity. The irradiosity is determined by integrating R along the

whole boundary of the gas domain, see [136]. Moreover, we have

R = E + J

ref

, (1.7)

E = σT

(Stefan-Boltzmann equation), (1.8)

ref

=(1− ) J, (1.9)

where E is the radiation, J

ref

is the reﬂexed radiation,  is the emissivity, and

σ is the Boltzmann radiation constant.

10Decomposition Methods for Diﬀerential Equations Theory and Applications

REMARK 1.2 The splitting methods are applied with respect to the

anisotropy in the diﬀerent dimensions. Therefore, a dimensional splitting can

accelerate the solver process and save memory resources, see [86] and [155].

In the next section, we focus on elastic wave propagation.

1.3.3 Elastic Wave Propagation

The motivation to study the elastic wave propagation came from the earth-

quake simulation. The realistic earthquake sources and complex three-

dimensional (3D) earth structure are of immense interest in understanding

the earthquake formation. A foundation for model ground motion in urban

sedimentary basins are studied and 3D software-packages are developed, see

[55] and [56]. Numerical simulations of wave propagation can be done in

two and three dimensions for models with suﬃcient realism (e.g., 3D geol-

ogy, propagating sources, frequencies approaching 1 Hz) to be of engineering

interest. Before numerical simulations can be applied in the context of en-

gineering studies or seismic hazard analysis, the numerical methods and the

models associated with them must be thoroughly validated, in this process

also the splitting methods are involved. Further the interest on simulating

accurate ground motion from propagating earthquakes in 3D earth models is

important. We propose the ﬁrst higher-order splitting method in this context

and have done the ﬁrst 3D simulations of simpler earthquake models to test

the accuracy of split equations and the conservation of the physical eﬀects.

The model problem is given with the physical parameters for the underlying

domains in which the earthquake occurs.

We present the model problem as an elastic wave equation for constant

coeﬃcients in the following notations:

ρ∂

U = μ∇

U +(λ + μ)∇(∇·U)+f, (1.10)

where U is equal to (u, v)

or (u, v, w)

in two and three dimensions, and f is

a forcing function. In seismology it is common to use spatial singular forcing

terms, which can look like

f = Fδ(x)g(t), (1.11)

where F is a constant direction vector. A numeric method for Equation (1.10)

needs to approximate the Dirac function δ(x) correctly in order to achieve full

convergence.

The contribution to this model is the initial process and spatial dependent

processes, which are started as a singular function (Dirac function) and are

computed in the later time-sequences as smooth functions. Therefore, large

time-steps are possible in the computation to simulate the necessary time-

periods.

Modeling: Multi-Physics Problems 11

REMARK 1.3 Here the splitting methods are applied with respect

to the later time-sequences to guarantee large time-steps. The diﬀerent spa-

tial dependent processes can be decoupled into Laplacian operators and non-

Laplacian operators. Such eﬀective decoupling allows us to accelerate the

solver-process of the simpler equations and save computational resources, see

[56] and [103].

1.3.4 Magnetic Trilayers

The motivation for the study is coming from modeling ferromagnetic mate-

rials, used in data storage devices and laptop displays. The models are based

on the Landau-Lifschitz-Gilbert equation, see [144], and are extended by the

interaction of diﬀerent magnetic layers. The application of such model prob-

lems includes switch processes in magnetic transistors (FET) or data devices.

Mathematically the equations cannot be solved analytically and numerical

methods are important. Therefore, numerical methods for stable discretiza-

tions are important because of the known blow-up eﬀects, see [19], [174]. We

apply the scalar theory and present the extention to more complicate systems

of magnetic models. In the numerical examples we present ﬁrst results of

single layers and inﬂuence with external magnetic ﬁelds.

In the mathematical model we deal with magnetic multi layers described

by the coupled Landau-Lifschitz-Gilbert equation.

The Landau-Lifschitz free energy E for the 2 layers is given as

E(m





1/2|∇m

+ φ(m

) (1.12)

+∇u, m



−h

ext,1

, m

 + A(m

, m

)) dx

E(m





1/2|∇m

+ φ(m

) (1.13)

+∇u, m



−h

ext,2

, m

 + A(m

, m

)) dx

A(m

, m



k=1

m

, m

 (1.14)

where m

is the magnetization vector in the layer i (i ∈{1, 2}), γ



> 0, the

saturation magnetization is given as M

s,i

for i ∈{1, 2}. h

ext,i

is the external

ﬁeld of layer i ∈{1, 2} .

For the magnetostatic case, the magnetic potential u

and the magnetization

are related through

Δu

= div(ξ

)inR

, (1.15)

where ω ⊂ R

is the domain covered by the ferromagnet, and ξ

=1onω

and 0 else.

The magnetic potential is also called a dipole ﬁeld.

12Decomposition Methods for Diﬀerential Equations Theory and Applications

REMARK 1.4 Here the splitting methods are applied with respect

to the diﬀerent layers. The physical decomposition into single-layer models is

performed. Such eﬀective decoupling allows us to accelerate the solver-process

of the physical simpler equations, see [19].

In the next chapter we discuss the decomposition analysis and discretization

methods to obtain the operator equations.

Chapter 2

Abstract Decomposition and

Discretization Methods

In this chapter we brieﬂy introduce the underlying ideas of the decomposition

analysis and discretization methods to obtain the abstract operator equations,

which are used and studied for our time decomposition methods.

2.1 Decomposition

In this section we discuss the decomposition of the evolution equations to

obtain separate underlying equations. The simpler equation parts are dis-

cretized to obtain an abstract operator equation formulation. Based on this

formulation we apply the decomposition methods, see Chapters 3 and 4 for

detailed explanations.

In the decomposition of the evolution equations, we deal with two main

problems:

• Decomposition of the evolution equation

• Decomposition methods to solve the decoupled evolution equation

The decomposition can be performed before the discretization, in which

case the physical behaviors of the operators are used to decide the type of

the splitting operators. Further, the decomposition can be done after the

space and time discretization of the partial diﬀerential equation, such that

the spectral analysis or stability conditions can be used to decide whether

operators are initiated for the splitting process.

We focus on the decomposition methods, which are applied after the space

discretization, and we obtain a system of ordinary diﬀerential equations. On

this level, the consistency and stability analysis can be treated on an abstract

level as a Cauchy problem in a more abstract level.

In the next subsection, we consider the decomposition of the evolution

equations and present two methods: the direct method called the physical

decomposition method and the more indirect method called the mathematical

decomposition method.

14Decomposition Methods for Diﬀerential Equations Theory and Applications

2.1.1 Decomposition of the Evolution Equations

The ﬁrst step of decomposing an equation into simpler problems is to ques-

tion the temporal, spatial, and physical scales of the equations.

In our work we contribute the temporal scales and propose two possible

mechanisms for decomposing an evolution equation:

• Physical decomposition

• Mathematical decomposition

In the physical decomposition we decompose the timescale due to the phys-

ical contributions (e.g., conservation laws, time discretization methods), that

are restricted by physical parameters (e.g., Courant-Friedrichs-Levy [CFL]

condition), or very dominant physical parameters (e.g., reaction scales), see

[94].

In the mathematical decomposition we underlie the operator equation and

solve an eigenvalue problem with respect to the possible operators for the

splitting method. We decide the splitting process taking the spectrum and

the maximal eigenvalues into account. A second and more abstract idea is a

decomposition involving only the spectrum of the operator, where we decouple

the spectrum of the operator and compute new operators using the spectrum

as a criterion for the timescales.

2.1.2 Physical Decomposition

For the physical decomposition method, the underlying physical parameters

determine in which operators the equation is decoupled. Often the choice of

the operators is obvious (e.g., for a problem in which the timescales of the

physical behaviors are known); in this case, the direct method is possible.

2.1.2.1 Direct Decoupling Method

Often the values of the physical parameters are so obvious that we can

determine the operators for the splitting methods.

The criteria for the direct decoupling method are strong anisotropy in the

space dimensions, obvious timescales (e.g., fast reaction process and slow

transport process, or diﬀerent physical scales (e.g., growth and decay pro-

cesses)).

For these obvious problems we can directly choose the form of the operators

(e.g., the ﬂow operator and reaction operator).

In an example for the direct decoupling method, we focus on the parabolic