Galdi G.P. An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems
Подождите немного. Документ загружается.


916 XIII Steady Navier–Stokes Flow in Domains with Unbounded Boundaries
With the help of Theorem XIII.2.1 we can readily obtain conditions under
which solutions determined in Theorem XIII.3.2 are unique. Actually, com-
bining Theorem XIII.2.1 with (XIII.3.2) we immediately find the foll owing
result.
Theorem XIII.3.3 Let v be a generalized solution to Leray’s problem con-
structed in Theorem XIII.3.2, corresponding to flux Φ. If
C
1 +
1
ν
+ 1
|Φ| + C
1 +
1
ν
|Φ|
2
<
ν
c
2
with c
2
and C given i n Theorem XIII.2.1 and T heorem XIII.3.2, respectively,
then v is the only generalized solution corresponding to Φ.
XIII.4 Decay Estimates for Steady Flow i n a
Semi–Infinite Straight Channel
Our objective in this section is to establish the rate at which solutions de-
termined in Theorem XIII.3.2 decay to the corresponding Poiseuille velo ci ty
fields. We shall show that, as |x| → ∞, they decay pointwise and exponentially
fast. As in the l inear case, this will follow as a corollary to a more general
result holding for a class of solutions wider than that determined in Theorem
XIII.3.2. More generality regards, essentiall y, the behavior at infinity, while a
restriction on Φ o f the type (XIII.3.1) is always needed.
We shall restrict our attention to flows occurring in the straight cylinder
Ω = {x
n
> 0} × Σ,
where the cross section Σ is a C
∞
–smooth, bounded, and simpl y connected
domain in R
n−1
(n = 2, 3). However, some o f the results we find can be
extended to cover more general situations. The cross section at distance a
from the origin will be denoted by Σ(a), despite all cross sections having the
same shape and size. Let v
0
= v
0
(x
0
) be the vector field associated with the
Poiseuille flow in Ω and corresponding to flux Φ. Further, let u , τ be a smooth
solution
1
to the following boundary-value problem:
ν∆u = u ·∇u + u · ∇v
0
+ v
0
· ∇u + ∇τ
∇ · u = 0
)
in Ω
u = 0 at ∂Ω − {x
n
= 0}
Z
Σ
u
n
= 0.
(XIII.4.1)
1
For simplicity, we assume u ,τ smooth, that is, indefinitely different iable in the
closure of any bounded subset of Ω. We note, however, that the same conclusions
may be reached merely by assuming that u and τ possess a priori the same
regularity of generalized solutions and then employing Theorem XIII. 1.1.

XIII.4 Decay Esti mates for Steady Flow in a Semi–Infinite Straight Channel 917
Remark XI II.4.1 If v is a generalized solution to Leray’s problem, then
u ≡ v − v
(i)
0
satisfies (XII I .4.1) with Ω ≡ Ω
i
, Σ ≡ Σ
i
and v
0
≡ v
(i)
0
.
We begin to show some local estimates for problem (XIII.4.1). To this end,
for R > 0 we let
Ω
R
= {x ∈ Ω : x
n
> R}.
Lemma XIII.4.1 Let u , τ be a smooth solution to (XIII.4.1) with
|u|
1,2
≤ M < ∞.
Then for every m ≥ 0 and R ≥ 0, the following estimate holds
kuk
m+2,2,Ω
R+1 + k∇τk
m,2,Ω
R+1 ≤ ckuk
1,2,Ω
R (XIII.4.2)
where c = c(n, m, M, Σ, Φ, ν).
Proof. Throughout the proof, the symbol c
i
, i = 1, 2, . . ., denotes a generic
quantity depending, at most, on m, M, Σ, and Φ. Let
0 < ε <
1
m + 2
. (XIII.4.3)
By (XIII.2.2)
2
and assumption, for all k = 0, 1, 2, . . ., and all R
1
≥ 0 we
derive
2
ku · ∇uk
3/2,Ω
R
1
+k,R
1
+k+1
≤ kuk
6,Ω
R
1
+k,R
1
+k+1
|u|
1,2,Ω
R
1
+k,R
1
+k+1
≤ c
1
|u|
1,2,Ω
R
1
+k,R
1
+k+1
and so, summing over k we obtain, in particular,
ku · ∇uk
3/2,Ω
R
1
≤ c
1
|u|
1,2,Ω
R
1
for a ll R
1
≥ 0.
In a similar fashion, from the H¨older inequality, the regularity of v
0
, and
inequality (XIII.2.4) we readily find
kv
0
· ∇u + u · ∇v
0
k
3/2,Ω
R
1
≤ c
2
|u|
1,2,Ω
R
1
for all R
1
≥ 0.
Thus, setting
f = u · ∇u + v
0
·∇u + u · ∇v
0
,
it follows that
kfk
3/2,Ω
R
1
≤ c
3
|u|
1,2,Ω
R
1
, for all R
1
≥ 0. (XIII.4 .4)
2
We give a proof that applies equally to both cases n = 2 and 3. However, f or
n = 2 the proof could be simplified.
918 XIII Steady Navier–Stokes Flow in Domains with Unbounded Boundaries
Employing (VI.1.13) with s = R
1
+ k, k = 0 , 1, 2, . . ., δ = ε and taking into
account (XIII.4.4), af ter summing over k we find
kuk
2,3/2,Ω
R
2
≤ c
4
kuk
1,2,Ω
R
2
−ε for all R
2
≥ 1.
From this relation and the first part of Lemma XIII.2.1 it then follows that
sup
Ω
R
2
|u| ≤ c
5
. (XIII.4.5)
Thus,
ku ·∇uk
2,Ω
R
2
≤ c
6
kuk
1,2,Ω
R
2
which, by the regularity properties of v
0
, in turn implies
kf k
2,Ω
R
2
≤ c
7
|u|
1,2,Ω
R
2
. (XII I.4.6)
We next employ (XIII. 4.5) together with (VI.1.13) calculated for s = R
3
+ k,
k ∈ N, and δ = ε. Summing over k and tak ing into account (XIII.4.5) we
deduce
kuk
2,2,Ω
R
3
+ k∇τk
2,Ω
R
3
≤ c
8
|u|
1,2,Ω
R
3
−ε , (XIII.4.7)
for a ll R
3
such that
R
3
≥ R
2
+ ε. (XIII.4.8)
We now cho ose
R
2
= R + ε , R
3
= R + 1. (XIII.4.9)
Since ε obeys (XIII.4.3) (wi th m = 0 ), it follows that (XIII.4.7) is satisfied
and that R
3
− ε = R + 1 − ε ≥ R. Therefore, (XIII.4 .7)–(XIII.4.9) prove
(XIII.4.2) for m = 0. Iterating this m ethod, it is possible to show the validity
of (XIII.4.2) for all m ≥ 0. We show this for m = 1, leaving to the reader
the proof of the general iterative procedure. By assumption, the first part of
Lemma XIII.2.1, and (XIII.4.5) it readily follows that
|u · ∇u|
1,2,Ω
R
3
≤ |u|
2
1,4,Ω
R
3
+ c
5
|∇u|
1,2,Ω
R
3
≤ c
9
(kuk
2
2,2,Ω
R
3
+ kuk
2,2,Ω
R
3
).
In view of (XIII.4.7) and the assumptions on u we deduce
|u · ∇u|
1,2,Ω
R
3
≤ c
10
kuk
1,2,Ω
R
3
−ε .
Likewise, from the regularity properties of v
0
and (XIII.4.7) we find
kv
0
· ∇u + u · ∇v
0
k
1,2,Ω
R
3
≤ c
11
kuk
1,2,Ω
R
3
−ε .
As a consequence, we infer that
kf k
1,2,Ω
R
3
≤ c
12
kuk
1,2,Ω
R
3
−ε . (XIII. 4.10)

XIII.4 Decay Esti mates for Steady Flow in a Semi–Infinite Straight Channel 919
We now employ (VI.1.13) with s = R
4
+ k, k ∈ IN and δ = ε. Summing over
k and taking into account (XIII.4.10), it follows that
kuk
3,2,Ω
R
4
+ k∇τk
1,2,Ω
R
4
≤ c
13
|u|
1,2,Ω
R
3
−ε , (XIII.4 .11)
for a ll R
4
such that
R
4
≥ R
3
+ ε (XIII.4.12)
where R
3
satisfies (XII I .4.8) with R
2
≥ 1. If we choose
R
2
= R + ε , R
3
= R + 2ε , R
4
= R + 1 ,
we see that, by (XIII.4.3) with m = 1, conditions (XIII.4.8) and (XIII.4.12) are
satisfied and, furthermore, R
3
−ε = R +ε > R. We then conclude the validity
of (XIII.4.2) with m = 1. The proof of the lemm a can be then considered
accomplished. ut
The conclusions of Lemma XIII.4.1 can be derived under much weaker as-
sumptions on the summability of ∇ u, provided that the flux Φ is “sufficiently
small.” To show this, we need a preliminary result concerning a differential
inequality.
Lemma XIII.4.2 Let y ∈ C
1
(IR
+
) be nonnegative with a nonnegative first
derivative. Assume for all t > 0
ay(t) ≤ a
1
y
0
(t) + a
2
(y
0
(t))
3/2
+ b (XI II.4.13)
where a is a positive constant while a
1
, a
2
, and b are nonnegative constants.
Then if
lim inf
t→∞
t
−3
y(t) = 0
we have
y(t) ≤ 2
b + 1
a
, for all t > 0. (XIII.4.14 )
Proof. From Young’s inequality (II.2.7) it foll ows that there is a c = c(a
1
)
such that for all t > 0
a
1
y
0
(t) ≤ c(y
0
(t))
3/2
+ b
1
where b
1
= b + 1. As a consequence, (XIII.4.13 ) yields
ay(t) ≤ d(y
0
(t))
3/2
+ b
1
(XIII.4.15)
with d = a
2
+ c. Assume (XIII.4 .14) is fal se, We can then find t
0
> 0 such
that
y(t
0
) > 2
b
1
a
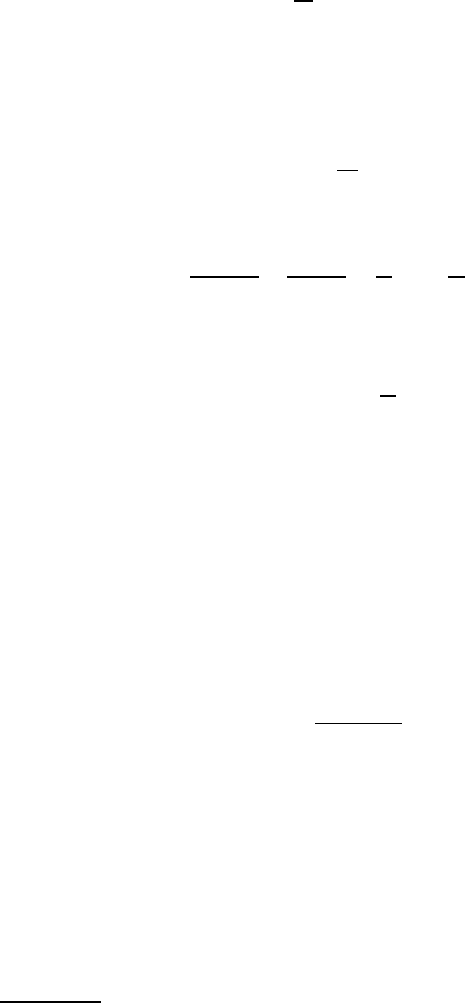
920 XIII Steady Navier–Stokes Flow in Domains with Unbounded Boundaries
and, since y
0
(t) ≥ 0,
y(t) > 2
b
1
a
for all t ≥ t
0
. (XIII.4.16)
Employing (XIII.4.16) in (XI II.4.15) we o bta in
A(y(t))
2/3
≤ y
0
(t), for all t ≥ t
0
with
3
A
2/3
≡
a
2d
> 0.
Integrating this inequality from t a nd t
1
> t, it follows that
y
1/3
(t
1
)
t
1
−
y
1/3
(t)
t
1
≥
A
3
1 −
t
t
1
and so taking the lim inf as t
1
→ ∞ of both sides of this inequality we derive
lim inf
t
1
→∞
t
−3
1
y(t
1
) ≥
A
3
3
> 0,
which contradicts the assumption. The lemma is therefore proved. ut
The result just shown allows us to prove the following.
Lemma XIII.4.3 Assume u, τ is a smooth solution to (XIII.4.1) such that
lim inf
x
n
→∞
x
−3
n
Z
x
n
0
(
Z
Σ(t)
|∇u(x
0
, t)|
2
dΣ)dt = 0.
Assume, further, that the flux Φ associated with the Poiseuille flow v
0
satisfies
|Φ| <
ν
(c
P
λµ)
1/2
, (XIII.4.17)
where c
P
is the constant given in Exercise VI.0.1 and λ, µ are given in
(XIII.2.3) and (XIII.2.4), respectively. Then
Z
Ω
∇u : ∇u < ∞.
Proof. Multiplyi ng (XIII.4.1)
1
by u and integrating by parts over (0, x
n
)×Σ,
we find
3
Notice that we can always take d > 0.

XIII.4 Decay Esti mates for Steady Flow in a Semi–Infinite Straight Channel 921
ν G(x
n
) ≡ ν
Z
x
n
0
"
Z
Σ(t)
∇u : ∇udΣ
#
dt
=
Z
Σ(x
n
)
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
−
Z
Σ(0)
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
−
Z
x
n
0
"
Z
Σ(t)
u ·∇v
0
· udΣ
#
dt
(XIII.4.18)
where v
0
= v
0
e
n
. By using the Schwarz inequality, (XIII.2.3), and (XIII.2.4)
we obtain
Z
x
n
0
Z
Σ(t)
u · ∇v
0
· udΣdt
≤
Z
Σ(t)
|∇v
0
|
2
!
1/2
Z
x
n
0
Z
Σ(t)
u
4
dΣ
!
1/2
dt
≤ (λµ)
1/2
Z
Σ(t)
|∇v
0
|
2
!
1/2
G(x
n
)
= (λµc
P
)
1/2
|Φ|G(x
n
),
(XIII.4.19)
where, in the last step, we have used the results of Exercise VI.0.1. Assuming,
now, the validity of (XIII.4.17) and setting
γ = ν − (λµc
P
)
1/2
|Φ| (> 0), (XIII.4.20)
from (XIII.4.1 8) and (XIII.4.19), it follows that
γG(x
n
) ≤
Z
Σ(x
n
)
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
+ b
with b a nonnegative quantity independent of x
n
. Integrating both sides of
this relation from t to t + 1 furnishes
γ
Z
t+1
t
G(x
n
)dx
n
≤
Z
Ω
t,t+1
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
+b. (XIII.4. 21)
We wish to estimate the term involving τ . To this end, we proceed as in
the linear case; see Theorem VI.2.1. Specifically, denoting by ω a solution to
(VI.2.14), from (XIII.4.1) we find
Z
Ω
t,t+1
τu
n
= −
Z
Ω
t,t+1
∇τ · ω
=
Z
Ω
t,t+1
[ν∇u : ∇ω − u ·∇ω ·u
−u · ∇ω·v
0
− v
0
·ω · u] .
(XIII.4.22)
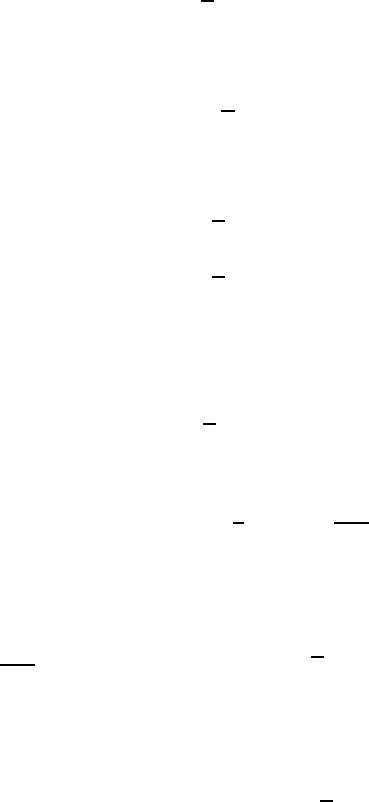
922 XIII Steady Navier–Stokes Flow in Domains with Unbounded Boundaries
Taking into account the properties of ω, from Lemma XIII.2.1 and (XIII.2.4)
we find
Z
Ω
t,t+1
∇u : ∇ω
≤ c
0
|u|
1,2,Ω
t,t+1
kuk
2,Ω
t,t+1
≤ c
0
√
µ|u|
2
1,2,Ω
t,t+1
Z
Ω
t,t+1
u · ∇ω · u
≤ c
0
kuk
2
4,Ω
t,t+1
kuk
2,Ω
t,t+1
≤ c
0
κ
2
√
µ|u|
2
1,2,Ω
t,t+1
Z
Ω
t,t+1
u · ∇ω·v
0
≤ c
0
bvkuk
2,Ω
t,t+1
|u|
1,2,Ω
t,t+1
≤ c
0
bv
√
µ|u|
2
1,2,Ω
t,t+1
Z
Ω
t,t+1
v
0
· ω ·u
≤ c
0
bv
√
µ|u|
2
1,2,Ω
t,t+1
(XIII.4.23)
with
bv = max
Σ
|v
0
(x
0
)|.
Putting
c
1
= c
0
√
µ(ν + κ
2
+ 2bv),
from (XIII.4.2 1)–(XIII.4.23) we deduce
γ
Z
t+1
t
G(x
n
)dx
n
≤ c
1
|u|
2
1,2,Ω
t,t+1
−
1
2
Z
Ω
t,t+1
ν
∂u
2
∂x
n
− u
2
(u
n
+ v
0
)
+ b.
(XIII.4.24)
We now observe that, again from (XI II.2.4) a nd Lemma XIII.2.1, it follows
that
Z
Ω
t,t+1
∂u
2
∂x
n
≤ 2kuk
2,Ω
t,t+1
|u|
1,Ω
t,t+1
≤ 2
√
µ |u|
2
1,Ω
t,t+1
Z
Ω
t,t+1
u
2
v
0
≤ bvµ|u|
2
1,Ω
t,t+1
Z
Ω
t,t+1
u
2
u
n
≤ kuk
2
4,Ω
t,t+1
kuk
2,Ω
t,t+1
≤ κ
2
√
µ |u|
3
1,2,Ω
t,t+1
.
(XIII.4.25)
Replacing these latter inequalities into (XI II.4.24), we find
γ
Z
t+1
t
G(x
n
)dx
n
≤ c
2
|u|
2
1,2,Ω
t,t+1
+ c
3
|u|
3
1,2,Ω
t,t+1
+ b (XIII. 4.26)

XIII.4 Decay Esti mates for Steady Flow in a Semi–Infinite Straight Channel 923
where
c
2
= c
1
+
√
µ(ν +
1
2
bv
√
µ)
c
3
=
1
2
κ
2
√
µ.
Setting
y(t) =
Z
t+1
t
G(x
n
)
and recalling the definition of G(x
n
), it follows that
y
0
(t) = |u|
2
1,2,Ωt,t+1
.
Therefore, i nequality (XIII.4.2 5) yields
γy(t) ≤ c
2
y
0
(t) + c
3
(y
0
(t))
3/2
+ b
which, in turn, by Lemma XIII.4.2, implies
y(t) ≤ 2
b + 1
γ
.
The result then follows from this estimate and an argument entirely analo gous
to that employed at the end of the proof of Theorem VI.2.1. ut
The next result establishes an exponential decay property of the type of
de Saint-Venant.
Lemma XIII.4.4 Let the assumptions of Lemma XIII.4.3 be satisfied. Then,
there are positive constants σ
i
= σ
i
(Σ, n, kuk
1,2,Ω
, Φ, ν), i = 1, 2, such that
kuk
1,2,Ω
R ≤ σ
1
kuk
1,2,Ω
exp(−σ
2
R), for all R > 0.
Proof. We notice that, in view of Lemma XIII.4.3, kuk
1,2,Ω
is finite. Multi-
plying (XIII.4.1)
1
by u and integrating by parts over (R, x
n
) ×Σ ≡ Ω
R,x
n
we
find
ν
Z
Ω
R,x
n
|∇u|
2
=
Z
Σ(x
n
)
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
−
Z
Σ(R)
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
−
Z
Ω
R,x
n
u · ∇v
0
· u .
(XIII.4.27)
From Lemma XIII.4 .1 and the embedding Theorem II.5.2 it follows, in par-
ticular, that
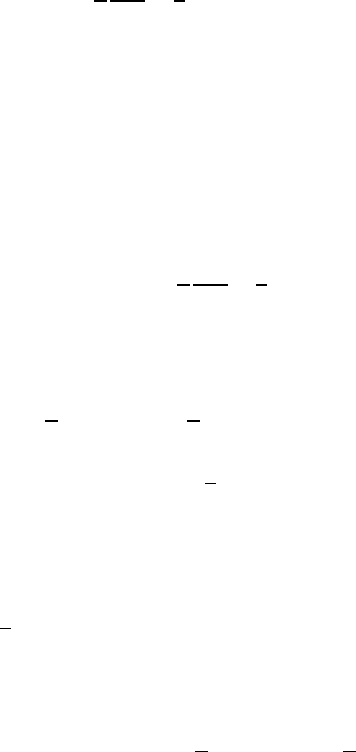
924 XIII Steady Navier–Stokes Flow in Domains with Unbounded Boundaries
sup
x
0
∈Σ
(|u(x
0
, x
n
)| + |τ(x
0
, x
n
)|) → 0 as x
n
→ ∞,
and so, reasoning as in the proof of Theorem VI.2.2, we can show that, in
the limit x
n
→ ∞, the surface integral over Σ(x
n
) is vanishing. Thus, in this
limit, (XIII. 4.27) yields
νH(R) = −
Z
Σ(R)
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
−
Z
Ω
R
u ·∇v
0
· u,
(XIII.4.28)
with
νH(R) ≡ ν| u|
2
1,2,Ω
R
.
Proceeding as in (XIII.4.19), we can show
Z
Ω
R
u · ∇v
0
· u
≤ (λµc
P
)
1/2
|Φ|H(R),
which, in view of (XIII.4.17), once replaced in (XII I.4.28) furnishes
γH(R) ≤ −
Z
Σ(R)
−τu
n
+
ν
2
∂u
2
∂x
n
−
1
2
u
2
(u
n
+ v
0
)
with γ given in (XIII.4.20). We next integrate bo th sides of this relati on
between t + l a nd t + l + 1, l = 0, 1, 2, . . ., to obtain
γ
Z
t+l+1
t+l
H(R) ≤ −
ν
2
Z
Σ(t+l+1)
u
2
+
ν
2
Z
Σ(t+l)
u
2
+
Z
Ω
t+l,t+l+1
τu
n
+
1
2
u
2
(u
n
+ v
0
)
.
(XIII.4.29)
The volum e integral on the right-hand side of (XIII.4.29 ) can be increased
exactly as i n (XIII.4.22), (XIII.4 .23), and (XIII.4.25)
2,3
and so we deduce
Z
Ω
t+l,t+l+1
τu
n
+
1
2
u
2
(u
n
+ v
0
)
≤ c
1
|u|
2
1,2,Ω
t+l,t+l+1
(1 + |u|
1,2,Ω
t+l,t+l+1
),
(XIII.4.30)
with c
1
= c
1
(n, Σ, Φ). Col lecting (XIII.4.29) and (XIII.4.30) we derive
γ
Z
t+l+1
t+l
H(R) ≤ c
2
|u|
2
1,2,Ω
t+l,t+l+1
−
ν
2
Z
Σ(t+l+1)
u
2
+
ν
2
Z
Σ(t+l)
u
2
(XIII.4.31)
where c
2
also depends on |u|
1,2,Ω
. Summing both sides of (XI II.4.31) from
l = 0 to l = ∞ and taking into account that, by Remark XIII.1.1
lim
t→∞
Z
Σ(t)
u
2
(x
0
, t)dΣ = 0,

XIII.4 Decay Esti mates for Steady Flow in a Semi–Infinite Straight Channel 925
we find
γ
Z
∞
t
H(R) ≤ c
2
H(t) +
ν
2
Z
Σ(t)
u
2
. (XIII.4.32)
However, by (XIII.2.4),
Z
Σ(t)
u
2
≤ µ
Z
Σ(t)
|∇u|
2
= −µH
0
(t)
and so from (XIII.4.32) we arrive at
γ
Z
∞
t
H(R) ≤ c
2
H(t) −
µν
2
H
0
(t).
Using Lemma VI.2.2 into this inequality furnishes the desired result and the
proof of the lemma is complete. ut
From Lemma XIII.4.1, Lemma XIII.4.3, and Lemma XIII.4.4, and with
the help of Lemma XIII.2.1, we are able to deduce at once the foll owing main
result.
Theorem XIII.4.1 Let u , τ be a smooth solution to (XIII.4.1) satisfying
lim inf
x
n
→∞
x
−3
n
Z
x
n
0
(
Z
Σ(t)
|∇u(x
0
, t)|
2
dΣ)dt = 0.
Then, if Φ satisfies (XIII.4.17), it follows that
kuk
1,2,Ω
< ∞.
Moreover, there is a positive constant c
1
= c
1
(Σ, n, Φ, kuk
1,2,Ω
, ν) such tha t
|D
α
u(x)| + |D
α
∇τ (x)| ≤ c
1
exp(−σ
2
x
n
) (XIII.4.33)
for every x ∈ Ω with x
n
≥ 1 and all |α| ≥ 0, and where σ
2
is given in Lemma
XIII.4.4.
This theorem, along with the uniqueness Theorem XIII.3.3 and the help
of Remark XIII.4.1 , immediately produces the following general result con-
cerning the asympto tic behavior of weak solutions to Leray’s probl em.
Corollary XIII.4.1 There exists a positive constant c = c(Ω, n) such that,
if
|Φ| < cν,
all generalized solutions v to Leray’s probl em (XIII.1.2)–(XIII.1.4) satisfy
the decay property (XIII.4.3 3) in each outlet Ω
i
, i = 1, 2 with u = v − v
(i)
0
and τ = p − C
i
.
