Galdi G.P. An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems
Подождите немного. Документ загружается.

796 XI Three-Dimensional Flow in Exterior Domains. Rotational Case
this connection, we would like to recall also the contribution of Silvestre (2004,
Theorem 3.1). Unlike Corollary XI.1.1, valid for any generalized solution, this
latter author proves the existence of at least one generalized solution satisfying
the pointwise property (XI.1.16).
Section XI.2. All results in this section are due to me.
Section XI.3. A proof of existence of generalized solutions under the as-
sumption that the boundary datum v
∗
(is sufficiently smooth and) has zero
total flux through ∂Ω is due to Leray (1933, Chapter III). If v
∗
reduces to
a ri gid motion, namely, v
∗
= v
1
+ v
2
× x, v
1
, v
2
∈ R
3
, a simpler proof is
given in Borchers (1992, Korollar 4.1). However, a similar result and under
the same boundary conditions can be easily deduced also from earlier work of
Weinberger (19 73) and Serre (1987).
The existence theory i n its full generality, as presented in Theorem XI.3.1,
is due to me.
Section XI.4. The main result, Theorem XI.4.1, is taken from Gal di & Kyed
(2011a , Theorem 4.4). As already pointed out in Remark XI.4.3, we would like
to emphasize one more time the interesting op en question whether v + v
∞
is square-summable in a neighborhood of infinity (that is, whether the liquid
possesses a finite kinetic energy), in the case that v
∗
≡ f ≡ 0 and v
0
·ω 6= 0.
Section XI.5. All results in this section are due to me. Simil ar results, under
more stringent assumptions on the data, can be found in Galdi & Kyed (2010,
2011a).
Section XI.6. The main results presented in Theorem XI.6.1–Theorem XI.6.3
are due to Galdi & Kyed (2011a). However, the proof of Theorem XI.6 .1 given
here differs in som e significant details from the analogous one furnished by
the above authors.
The significant problem that is left open is the determination of leading
terms (if any) in the asym pto tic expansion of the velocity and pressure fields.
Another interesting problem that deserves attention is the asymptotic be-
havior of the vorticity field. It is very likely that outside the “wake region”
the vorticity decays exponentially fast. Nevertheless, a proof of this property
is far from being obvious.
Section XI.7. Theorem XI.7 .1 is basically due to Galdi (2003) and Galdi &
Kyed (2010).
The fa ct that a suitable Landa u solution is the leading term in the asymp-
totic expansion of the velocity field was first discovered by Farwig & Hishida
(2009). In fact, the mai n result of these authors, under assumptions slightly
different from those of Theorem XI.7.4, consists in the proof o f a representa-
tion for v similar to (XI.7.9), where, however, the quantity v + v
∞
− U
b
is
estimated in Lebesgue spaces rather than pointwise.

XII
Steady Navier–Stokes Flow in
Two-Dimensional Exterior Domains
F.F. CHOPIN, Scherzo op.31, bars 1-3.
Introduction
In this chapter we shall study plane steady flow occurring in the complement
of a compact region. Specifically, we shall investigate existence, uniqueness
and asymptotic behavior of solutions v, p to the Navier–Stokes system:
1
∆v = Rv · ∇v + ∇p + Rf
∇· v = 0
)
in Ω
v = v
∗
at ∂Ω
(XII.0.1 )
where Ω is an exterior domain of R
2
. As in the previous chapter, (XII.0.1) is in
a nondimensional form, with R representing the Reynolds number. To system
(XII.0.1 ) we must append the conditi on at infinity on the velocity field, tha t
we choose to be of the form
1
As we mentioned previously in several occasions, the steady-state, two-
dimensional exterior problem in a rotating frame still lacks of significant results.
For this reason, it will not be treated in this monograph.
797G.P. Galdi, An Introduction to the Mathematical Theory of the Navier-Stokes Equations:
Steady-State Problems, Springer Monographs in Mathematics,
DOI 10.1007/978-0-387-09620-9_12, © Springer Science+Business Media, LLC 2011

798 XII Two-Dimensional Flow in Exterior Domains
lim
|x|→∞
v(x) = −v
∞
, (XII.0.2 )
with v
∞
a prescribed (constant) vector of R
2
. As already pointed out, a
significant application of problem (XII.0.1)–(XII.0.2) occurs when f ≡ v
∗
≡ 0
and v
∞
6= 0, and regards the steady-state motion of a viscous liquid around a
long, straight cylinder C with axis a, assuming that the liquid is at rest at large
distances from C, and that C moves with (constant) translational velocity v
∞
orthogonal to a. Actually, in a region of flow sufficiently far from the two ends
of C and including C, one may expect that the velocity field of the liquid is
independent of the coordinate parallel to a and, moreover, that there is no
motion in the direction o f a. Therefore, the relevant region of flow can be
reasonably approximated by a two-dimensional domain placed in a suitable
plane orthogonal to a and exterior to the cross-section of C.
Using the methods of Section X.4 (cf. Remark X.4.4), we show that if Ω is
locally Lipschitz with ∂Ω 6= ∅, and if the flux of v
∗
through ∂Ω is sufficiently
“small” in the sense of (X.4.47), then (XII.0.1) admits at least one sol ution
v, p, without further restrictions on the size of the data. Such a solution is
also smooth if Ω and the data are likewise smooth. Concerning the behavior
at large distances, the only informa tion one can obtain is that v has a finite
Dirichlet integral, that i s,
Z
Ω
∇v : ∇v ≤ M, (XII.0.3)
with M = M (Ω, f, v
∗
, R). However, (XII.0.3) alone is not enough to ensure
that v tends (even in a generalized sense) to a constant vector to infinity, as
is shown by simple counterexamples; see Section XII.1.
2
Therefore, we don’t
know if these solutions verify condition (XII.0.2). Furthermore, if v
∗
≡ f ≡ 0,
we do not know, in general, if this solution is nontrivial.
3
A separate consid-
eration deserves the case Ω = R
2
. Actually, in such a case, even the existence
of solutions to the system (XII.0.1) is not known, in general.
4
Technically, this
is due to the fact that a sequence of functions obeying the bound (XII.0.3)
with Ω = R
2
, need not be convergent in any of the spaces L
q
(B
R
), q > 1,
R > 0 (cf. Exercise II.7.3), and this in turn implies that one can not show
the convergence of the nonlinear term along the sequence of approximating
solutions; see Remark X.4.4 .
The investigatio n of whether solutions to (XII.0.1 ) satisfying (XII.0.3) may
also obey (XII.0.2) has a ttracted the attention of many writers; see Section
XII.3. Specifically, Gilbarg & Weinberger (1974, 1978) have shown that if f is
2
A sharp estimate at large distances of functions satisfying condition (XII.0.3) has
been given in Theorem II.9.1.
3
If Ω
c
is symmetric around some direction, then one can construct nontrivial,
suitably symmetric solutions; see the Notes for this Chapter.
4
Existence can be established if the data satisfy suitable symmetry requirements;
see the Notes for this Chapter.

XII Introduction 799
of bounded support, every v satisfying (XII.0.1) for a suitable pressure p, and
(XII.0.3 ), either converges at large distances, in a well-defined sense, to some
constant vector v
0
, or that the L
2
-norm of v over the unit circle approaches
infinity at large distances. However, they can not show that v
0
= −v
∞
. If
v
∗
≡ f ≡ 0, Amick (1988) has proved that v ∈ L
∞
(Ω). Nevertheless, also i n
such a case, one cannot infer that v
0
= −v
∞
if v
∞
6= 0 and, wha t perhaps
is more surprising, if v
0
= 0, one is able to conclude that v ≡ 0 only in the
special situation where Ω = R
2
.
At this point we may wonder if we could prove existence by means of
different techniques, such as a fixed po int argument. This problem, which was
first considered by Finn & Smith (196 7b), is in fact solvable when the velocity
field v
∞
is not zero and the data are sufficiently sm all; see Section XII.5. It
is interesting to observe that the corresponding solutions obey, in particular,
condition (XII.0.3). It should also be empha sized that if v
∞
= 0, the above
techniques do not work and so it is no t known whether (XII.0.1), (XII.0.2)
with v
∞
= 0 is resoluble, even for small data.
5
The reason for this unequal
result i s essentially due to the fact that the approach followed is based on
fixed point arguments that rely on linearized versions of (XII.0.1), (XII.0.2).
As we know from Chapters V and VII, the linearization when v
∞
6= 0 (Oseen
system) produces solutions that, in the neighborho od of infinity, are more
regular than those corresponding to the linearization when v
∞
= 0 (Stokes
system). In this respect, we recall that a simila r circumstance occurs also for
three-dimensional flows.
In view of all the above, it is natural to ask whether (XII.0.1)–(XII.0 .2)
may indeed admit a solution for data of arbitrary si ze. This question has
been investigated by Galdi (1999b) for the physically relevant problem where
v
∗
≡ f ≡ 0, which, as we noted previously, describes the motion of the liquid
past a sufficiently long cylinder. In such a case the data are represented by
the translational velocity of the cylinder that, in dimensionless form, is given
by Re
1
(assuming v
∞
ke
1
). Let us call P this parti cular problem. “Arbitrary
data” for P means then “arbitrary speed” of the cylinder, namely, any R > 0.
Galdi has shown tha t if Ω possesses an axis of symmetry (e.g., Ω is the exterior
of a circle) then, if there exists R > 0 such that for all R ≥ R problem P
has no solution in a very general regularity class, the homogeneous problem
obtained by setting in (XII.0.1)–(XII.0.2) v
∗
≡ f ≡ v
∞
≡ 0, and R = 1
must admit a non-zero solution, a fact that is very questionable on physical
grounds; see Section XII.6.
Another question that arises is the asymptotic structure of a field v satis-
fying (XII.0.1)–(XII.0.3), for suitable p. One may expect that v can be rep-
resented asymptotically by an expansion in “reasonable” functions of r ≡ | x|
with coefficients independent of r. However, if v
∞
= 0, not every such solution
can be represented in this way, for one can exhibit examples, due to Hamel,
of solutions to (XII.0.1), (XII. 0.2) with v
∞
= 0 that obey (XII.0.3) and decay
5
See, however, the Notes for this Chapter for some partial results.

800 XII Two-Dimensional Flow in Exterior Domains
more slowly than any negative power of r; see Section XII.6. If v
∞
6= 0 , how-
ever, we have a result completely analogous to the three-dimensional case,
namely, if v satisfies (XII. 0.1)–(XII.0.3), for a suitable pressure p, and, in
addition, f is (sufficiently smooth and) of bounded support, then v has the
same asymptotic structure of the Oseen fundamental solution. The proof of
this result, based on the papers of Galdi & Sohr (1995) and Sazonov (1999),
is due to Sazonov; see Section XII.6 and Section XII.8.
In the last section of the chapter we shall study the behavior of solutions
to (XII.0.1), (XII.0.2) in the limit of vanishing Reynolds number for the case
f = 0.
6
This problem is considered in the class C of solutions whose existence
has been determined in Section XII.5. We show that the solutions from C
tend (in an appropriate sense) to solutions of the Stokes probl em obtai ned
by formally taking R = 0 into (XII.0.1), (XII. 0.2). The interesting feature of
this study is that, as expected from the linear theory (cf. Section VII.8), the
limit process is singular in that it does not preserve the condition at infinity
(XII.0.2 ). In fact, following the work of Ga ldi (1993), we show that the limit
solution satisfies (XII.0.2) if and only if v
∗
verifies a suitable condition. In
the case when Ω is the exterior of a unit circle, this condi tion reads:
Z
∂Ω
(v
∗
+ v
∞
) = 0.
Notation. Throughout this chapter Cartesian coordinates of a point x, are
denoted either (as usual) by x
1
, x
2
, or (more simply) by x,y. When using the
latter notation, the components of a vector w are written as w
x
, w
y
. We shall
also frequently employ polar coordinates, r,θ. In such a case, the components
of w, are denoted, as customary, by w
r
, w
θ
.
XII.1 Gene ralized Solutions and D-Soluti ons
As already observed in Remark X.4.4, if Ω is a l ocally Lipschitz exterior do-
main in the plane with ∂Ω 6= ∅, and if the flux of v
∗
through ∂Ω satisfies
(X.4.47), we may use the same method employed in Section X.4 to construct,
for all R > 0, a vector field satisfying conditions (i)-(iii) and (v) of Definition
IX.1. 1, together with the energy inequali ty (IX.4.16). Moreover, we can asso-
ciate to v a pressure field p (cf. Lemma X.1.1) and both v and p are smooth
provided Ω and the data are smooth; cf. Theorem X.1.1. However, v and p
solve in principle only problem (XII.0.1) because, unlike the three-dimensional
case, the property (i), namely,
Z
Ω
∇v : ∇v < ∞, (XII.1.1)
is not enough a priori to control the behavior at infinity of v. Thus, the limiting
condition (XII.0.2) or even the weaker condition (iv) of Definitio n X.1.1 need
6
This assumption is made for the sake of simplicity.

XII.2 On the Uniqueness of Generalized Solutions 801
not be satisfied. That the problem of proving the convergence at infinity of a
solution v under the sole information (XII.1.1) is far from being obvious, i s
shown by the fact that there are fields w in Ω having a finite Dirichlet integral
and that become unbounded at large distances like a power of log |x|. Take,
for instance, Ω = R
2
− B(0) and w(x) = (log |x|)
α
, 0 < α < 1/2. Therefore,
in order to prove the convergence of a solution v at infinity, the equations of
motion must play a f undamental role.
The situation becomes completely obscure in the case Ω = R
2
, where the
methods of Section X.4 do not even furni sh existence of a vector field satisfying
(XII.0.1 ) for a suitable pressure p; see Remark X.4.4.
In what follows, we will make a definite distinction between a generalized
solution v to (XII.0.1), (XII.0.2) in the sense of Definition X.1.1, and a field
v sati sfy ing only (i)-(iii) and (v) of the same definition. In this latter case,
the vector field v will be referred to as a D-solution, in spite of the fact that
the word “solution” is not the most appropriate, since v need not verify the
condition at infinity. A study on the asymptotic behavior of D-solutions i s
performed in Section XII.3, where it will be shown, among other things, that,
as |x| → ∞, v(x) tends in a suitable sense to some vector v
0
. Whether this
vector coincides with the vector −v
∞
prescribed in (iv) of Definition X.1.1
remains, however, a fundamental open question.
Nevertheless, we may wonder if, by using a different technique, one can
show existence, at least in the range of small data. As shown in Section XII.5,
this is indeed possible, provided v
∞
is not zero. If v
∞
is zero, the questi on of
existence of generalized solutions, even with small data, is open and, probably,
for “generic” data, it does not admi t a positive answer; see also the Notes for
this Chapter.
XII.2 On the Uniqueness of Generalized Solutions
Maybe uniqueness of generalized solutions is a more complicated question
than existence itself. I ndeed it represents a formidable problem that, for its
resolution, requires in my opi nion the contribution o f completely new ideas
and methods. To test the difficulty, let v
1
, p
1
and v
2
, p
2
be two generalized
solutions to problem (XII.0.1), (XII.0.2), which will be assumed smooth for
simplicity. Letting
u = v
1
− v
2
π = (p
1
−p
2
)/R
we have
1
R
∆u = u · ∇u + v
1
· ∇u + u · ∇v
1
+ ∇π
∇ · u = 0
in Ω
u = 0 at ∂Ω
lim
|x|→∞
u(x) = 0.
(XII.2.1 )

802 XII Two-Dimensional Flow in Exterior Domains
Multiply (XII.2.1)
1
by u, integrate by parts over Ω
R
and use (XII.2.1)
2
to
obtain
R
−1
Z
Ω
R
∇u : ∇u = −
Z
Ω
R
u·∇v
1
·u+
Z
∂B
R
[u·
∂u
∂n
−
1
2
u
2
(u+v
1
)·n−πu ·n].
(XII.2.2 )
Now assume tha t u, v
1
, and π behave in such a way that the surface integral
tends to zero as R → ∞. (This is not known if v
∞
= 0, while, if v
∞
6= 0,
it is true for any generalized solution which satisfies some further condition;
cf. Section XII.8.) From (XII.2.2) in the limit R → ∞ we find
R
−1
Z
Ω
∇u : ∇u = −
Z
Ω
u · ∇v
1
· u. (XII. 2.3)
This is the classical relation, which we have used several times to show unique-
ness o f generalized solutions, sometimes with the equality sign replaced by the
inequality one. However, for the case at hand, relation (XII.2.3) is not g oing
to produce uniqueness for smal l R. Actually, we would need a n estimate of
the type
−
Z
Ω
u · ∇v
1
· u ≤ c
Z
Ω
∇u : ∇u (XII.2.4)
for som e c = c(v
1
, Ω) ∈ (0, ∞), to conclude
Z
Ω
∇u : ∇u = 0, for R < c
−1
,
and hence uniqueness. However, the validity of (XII.2.4) is very unlikely,
1
no matter what summabil ity assumptio ns on u and v
1
are made and, con-
sequently, the “traditional” method gives no information whatsoever about
uniqueness, even at small Reynolds numbers.
Nevertheless, what is certainly true i s that, if R is “ sufficiently” large and
the flux through the wall ∂Ω is not zero, uniqueness of generalized solutions is
lost, as can be seen by means of sim ple examples. To show this, let us consider
an indefinite, circular cylinder C of radius r
0
immersed in a viscous liquid and
assume that the radial comp onent of the velocity of the liquid, when evaluated
at the lateral surface of C, is a constant V. The appropriate Reynolds number
is then defined by
R = V r
0
/ν.
Using V and r
0
as reference velocity and length, respectively, from (XII.0.1),
(XII.0.2 ) we obtain that the two-dim ensional moti ons of the liquid in every
plane orthogonal to C, w hen referred to polar coo rdinates (r, θ), must obey
the following problem
1
From (I I.5.7) it follows that (XII.2.4) holds if ∇v
1
(x) = O(|x|
−2
log
−2
|x|).
However, even admitting that v
1
at large distances has the same behavior
as the solution of the corresponding linearized problem, we would have only
∇v
1
(x) = O(|x|
−1
); cf. Section V.3 and Section VII.6.
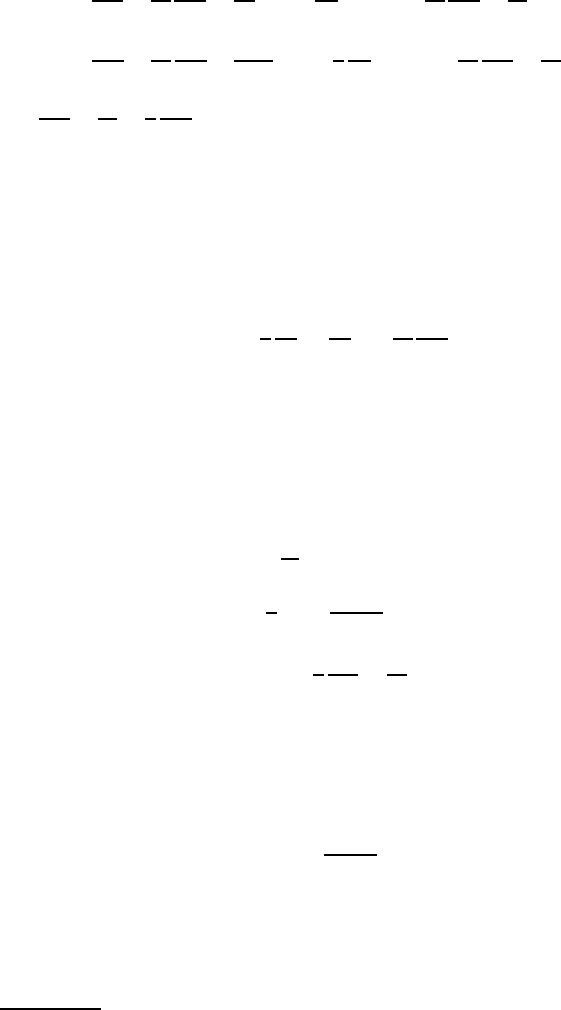
XII.2 On the Uniqueness of Generalized Solutions 803
R
v
r
∂v
r
∂r
+
v
θ
r
∂v
r
∂θ
−
v
2
θ
r
= −
∂p
∂r
+ ∆v
r
−
2
r
2
∂v
θ
∂θ
−
v
r
r
2
R
v
r
∂v
θ
∂r
+
v
θ
r
∂v
θ
∂θ
+
v
θ
v
r
r
= −
1
r
∂p
∂θ
+ ∆v
θ
+
2
r
2
∂v
r
∂θ
−
v
θ
r
2
∂v
r
∂r
+
v
r
r
+
1
r
∂v
θ
∂θ
= 0
in Ω
v(1, θ) = v
∗
lim
r→∞
v(r, θ) = −v
∞
(XII.2.5 )
where v = (v
r
, v
θ
), Ω is the exterior of the unit circle, v
∗
(θ) is prescribed and
∆ =
1
r
∂
∂r
r
∂
∂r
+
1
r
2
∂
2
∂θ
2
.
Now, by a simple computation, we show that for any choice of γ, ω ∈ R and
R > 1, R 6= 2, problem (XII.2.5) with
v
∞
= 0, v
∗
= (−R, γ − ω/(R− 2)) (XII.2.6)
admi ts the elementary solution
2
v
r
= −
R
r
v
θ
=
1
r
γ −
ω
R−2
r
−R+2
p = R
Z
1
2
dv
2
r
dr
−
v
2
θ
r
.
(XII.2.7 )
The flow (XII.2.6), (XII.2.7) which was discovered by Hamel (1916, pp. 51-52)
has a simple physical explanation; cf. Preston (1950). Specifically, it represents
the motio n of a liquid subject to a uni t suction in the direction orthogonal to
the wall of the circular cylinder, while the cylinder rotates with the angular
velocity
γ −
ω
R− 2
.
By the arbitrarity of R, γ, and ω, we may choose
ω = γ(R − 2) (XII.2.8)
and the solution (XII.2.7) special izes to
2
Notice that (XII.2.7) is not a solution of the corresponding linearized Stokes
problem, that is, (XII.2.5) with R = 0, since (XII.2.5)
5
is violated.

804 XII Two-Dimensional Flow in Exterior Domains
v
r
= −
R
r
v
θ
=
ω
R− 2
1
r
1 − r
−R+2
p = R
Z
1
2
dv
2
r
dr
−
v
2
θ
r
.
(XII.2.9 )
Moreover, the data are independent of γ, since with the choice (XII.2 .8) and
for R > 1 and R 6= 2, conditions (XII.2.6) become
v
∞
= 0, v
∗
= (−R, 0). (XII.2 .10)
As a consequence, we conclude that if R > 1 and R 6= 2 the fields (XII.2.9)
constitute a one-parameter family of solutions to (XII.2.5), parameterized in
ω, and corresponding to the same da ta (XII.2.10). Furthermore, since the
gradients of the velocity fields square summable in Ω, they are generalized
solutions.
The example just given suggests that, in the exterior two-dimensional
problem, the prescription of the velocity field alone at the boundary and at
infinity is not in general enough to secure the uniqueness o f the solutio n, and
other extra conditions may be needed. For instance, in the class (XII.2.9)–
(XII.2.1 0) uniqueness is recovered if we prescribe at the boundary r = 1 the
vorticity ω = r
−1
∂(rv
θ
)/∂r.
XII.3 On the Asymptotic Behavior of D-Solutions
The aim of this section is to investigate the behavior at large distances
of D-solutions, namely, of vector fields v satisfying (XII.0.1) and condition
(XII.1.1 ).
Since we are interested onl y in the regularity at infinity, we shall suppose
that the D-solutions with which we a re dealing are as smooth as required
by the formal manipulation we shall perform. Of course, to substantiate this
procedure, it is enough to assume that the data and the domain Ω have a
sufficient degree of regularity, what degree will b e tacitly understood. More-
over, since the results we shall find are essentially independent of the Reynolds
number R, we shall put, for simplicity, R = 1.
We wish now to collect some notation and fo rmulas that will be frequently
used. T he scalar field
ω =
∂w
x
∂y
−
∂w
y
∂x
is the vorticity of a vector field w. From (XII.0 .1), it follows that the vorticity
of a D-solution v verifies the equation
∆ω − v · ∇ω =
∂f
x
∂y
−
∂f
y
∂x
. (XII.3.1)
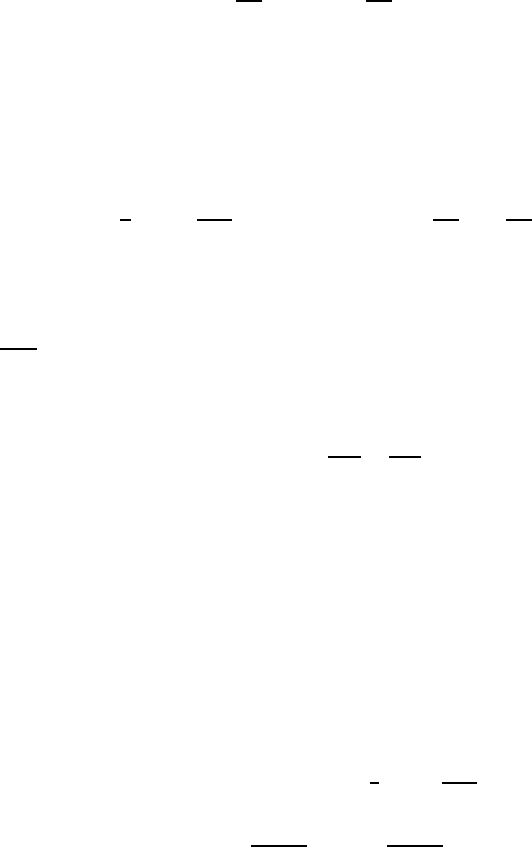
XII.3 On the Asymptotic Behavior of D-Solutions 805
Owing to the solenoidality of v, we also have
∆v
x
=
∂ω
∂y
, ∆v
y
= −
∂ω
∂x
. (XII.3.2)
The fo llowing result is based on ideas of Gilbarg & Weinberger (1978, Lemma
2.3).
Lemma XII.3.1 Let v be a D-solution to (XII.0.1) with f ∈ L
2
(Ω
ρ
), some
ρ > δ(Ω
c
). Then, ∇ω ∈ L
2
(Ω
ρ
) and the following identity holds
Z
Ω
|∇ω|
2
=
1
2
Z
∂B
ρ
∂ω
2
∂n
− v · nω
2
+
Z
Ω
ρ
f
y
∂ω
∂x
−f
x
∂ω
∂y
.
Proof. Let h ∈ C
1
(R) be a positive function with piecewise differentiable
first derivatives and let ψ
R
be the Sobolev “cut-off” function (II.6.1 ) with
exp
√
ln R > ρ. Using (XII.3.1), we show the following identity
∇ · [ψ
R
∇h − h∇ψ
R
−ψ
R
hv] = ψ
R
h
00
|∇ω|
2
− h (∆ψ
R
+ v · ∇ψ
R
)
+ h
0
ψ
R
∂f
x
∂y
−
∂f
y
∂x
,
(XII.3.3 )
where prime means differentiation. Setting
ω
∗
= max
x∈∂B
ρ
|ω(x)|,
we choose
h =
(
ω
2
if |ω| ≤ ω
0
ω
0
(2|ω| −ω
0
) if |ω| ≥ ω
0
(XII.3.4 )
for ω
0
≥ ω
∗
. From (XII.3.3) and (XII.3.4) we easily recover
Z
Ω
ρ
h
00
ψ
R
|∇ω|
2
=
Z
Ω
ρ
h(∆ψ
R
+ v · ∇ψ
R
) +
1
2
Z
∂B
ρ
∂ω
2
∂n
−v ·nω
2
+
R
Ω
ρ
f
y
∂h
0
ψ
R
∂x
− f
y
∂h
0
ψ
R
∂x
.
(XII.3.5 )
Taking into account that
h ≤ min
ω
2
, 2 ω
0
|ω|
and the properties (II.6.2), (II.6.5), and (II.6.6
1
) of the function ψ
R
, we find
