Galdi G.P. An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems
Подождите немного. Документ загружается.


146 III The Function Spaces of Hydrodynamics
Proof. From Exercise III.1.1 we know that H and G are orthogonal subspaces
in L
2
. Moreover, suppose that u belongs to H
⊥
. By Lemma III.1.1 there
exists a scalar function p ∈ L
1
loc
(Ω) such that u = ∇p and, by Lemma II.6.1,
p ∈ L
2
loc
(Ω) thus showing u ∈ G, which completes the proof. ut
The study of the validity of the decomposition (III.1.5) when q 6= 2 turns
out to be more involved, due to the fact that L
q
ceases to b e a Hilbert space.
However, if q ∈ (1, ∞), it is not hard to show that the decomposition is
equivalent to the unique solvability of a suitable Neumann problem. Actually,
consider the following problem NP: Given
u ∈ L
q
(Ω)
to find a unique (up to a constant) function p : Ω → R such that
(i) p ∈ D
1,q
(Ω);
(ii)
Z
Ω
(∇p − u) · ∇ϕ = 0, for all ϕ ∈ D
1,q
0
(Ω).
The reader will check with no pain that i f Ω has a sufficiently smooth
boundary and u is regular enough, NP implies the existence of a solution
p ∈ D
1,q
(Ω) to the fol lowing classical Neumann problem:
∆p = ∇ · u in Ω
∂p
∂n
= u · n at ∂Ω.
(III.1.10)
The next lemma gives a characterization of the validity of the Helmholtz–
Weyl decomposi tion.
Lemma III.1.2 The Helmholtz–Weyl decompositi on of L
q
(Ω), 1 < q < ∞,
holds if and only if NP is solvable for any u ∈ L
q
(Ω).
Proof. Denote by HW the Helmholtz–Weyl decomposition. Let us first show
that NP implies HW. Given u ∈ L
q
(Ω), set
w = u − ∇ p, (III.1.11)
with p (unique) solution to NP. It is easy to see that w ∈ H
q
(Ω). In fact, by
(ii) we deduce
w ∈ G
⊥
q
0
.
On the other hand, by Lemma III.1. 1 and by the Riesz representation theorem,
it is
H
⊥
q
⊂ G
q
0
, 1 < q < ∞.
Therefore,
w ∈ (H
⊥
q
)
⊥
∩ L
q
,
III.1 The Helmholtz–Weyl Decomposition of the Space L
q
147
and so, by well-known properties on annihilators (see, e.g., Kato 1966, p. 136)
we conclude w ∈ H
q
. To prove HW completely, it remains to show that the
representation obtai ned for u from (III.1.11) is indeed unique. This amounts
to proving that the equality
w = ∇p, w ∈ H
q
(Ω), p ∈ D
1,q
(Ω) (III. 1.12)
is possible if and only if w ≡ ∇p ≡ 0. Let us show that this is certainly so in
our case. In fact, from (III.1.12) and Exercise III.1.1(b) we have
Z
Ω
∇p · ∇ϕ = 0 for all ϕ ∈ D
1,q
0
(Ω),
which, in turn, by the uniqueness of solutions to NP and (III.1.12) i mplies
w ≡ ∇p ≡ 0. Conversely, assume that HW holds. Then, given u ∈ L
q
(Ω) we
may decompose u as i n (III.1.6) where w
1
= ∇p, p ∈ D
1,q
(Ω). Multiplying
this relation by ∇ϕ, ϕ ∈ D
1,q
0
(Ω), and integrating over Ω, we obtain
Z
Ω
(∇p − u) · ∇ϕ = −
Z
Ω
w
2
·∇ϕ, w
2
∈ H
q
(Ω).
In view of Exercise III.1.1(b),
Z
Ω
w
2
· ∇ϕ = 0,
so that p satisfies (ii). By the uniqueness of the representation (III.1.6), we
have that such a p is unique (up to a constant). The lemma is proved. ut
Remark III.1.2 Theorem III.1.1 and Lemma III.1.2 imply that, f or q = 2,
the corresponding generalized Neumann problem NP admits a unique solu-
tion in a n arbitrary domain Ω.
We shall next present a wide class of domai ns for which NP is solvable.
The simplest situation occurs when Ω = R
n
for, in this case, fo r u ∈ C
∞
0
(R
n
),
we can produce an explicit sol ution, that i s (see Exercise II.11.3),
p(x) =
Z
R
n
E(x − y)∇ · u(y)dy. (III. 1.13)
It is easy to show that (III.1.1 3) satisfies all the requirements. In fact, on the
one hand, by Exercise II.11.7 and by the Calder´on–Zygmund Theorem II.11.4,
it follows that (i) is accomplished and, moreover, that
|p|
1,q
≤ ckuk
q
. (III.1.14)
On the other hand, si nce u vanishes outside a compact set K (say), we also
have for sufficiently large R

148 III The Function Spaces of Hydrodynamics
Z
B
R
(∇p − u) ·∇ϕ = −
Z
∂B
R
ϕ
∂p
∂n
, (II I.1.15)
where ϕ ∈ D
1,q
0
(R
n
). From (III.1 .13) it is easily seen that for x outside K
∇p(x) = O(|x|
−n
). (III.1.16)
Furthermore, ϕ o beys the estimate (see Exercise II.6.3 )
Z
S
n
|ϕ(x)| = o(|x|). (III.1.17)
Thus, from (III.1.15)–(III.1.17), in the l imit R → ∞ we deduce (ii) of the
definition of NP. Finally, uniqueness is obtained with the help of Exercise
II.11.11. It is now easy to extend the results just shown to the case when
u is an arbitrary function in L
q
(Ω). This will be achieved through a stan-
dard approximating procedure based on (III.1.14). Actually, by the density
properties recalled in Section II.2, we can approximate u with a sequence
{u
m
} ⊂ C
∞
0
(Ω). For each u
m
we solve NP as before and denote by p
m
the
corresponding solution. Using (III.1.14) and the uniqueness property we then
prove that { [p
m
]} is a Cauchy sequence in
˙
D
1,q
(Ω), and so, by Lemma II.6.2,
there exists [p] ∈
˙
D
1,q
(Ω) such that
|[p
m
] − [p]|
1,q
→ 0, m → ∞.
It is easy to verify that p
0
∈ [p] uniquely satisfies (up to a constant) condition
(ii) stated for NP, thus proving the desired decomposition of L
q
(R
n
) for all
q ∈ (1, ∞).
Analogous reasoning can be used if Ω is the half space R
n
+
. In this case
too, in fact, we have an explicit formula for p:
p(x) =
Z
R
n
+
N(x, y)∇ · u(y)dy, x ∈ R
n
+
, (III.1.18)
where
N(x, y) ≡ E(x − y) + E(x − y
∗
), y
∗
= (y
1
, . . . , y
n−1
, y
n
)
is the (Neumann) Green’s function of the Laplace operator in R
n
+
; see Exercise
III.1.5. The details of the proof are left to the reader (see also McCracken
1981).
If Ω has a sufficiently smoo th bounded boundary, the problem NP is still
solvable but, of course, in a more involved way.
Actually, if Ω is a bounded domain of class C
2
, a solution to NP can
be determined as a consequence of more general results on elliptic problems
established by Lions & Magenes (1 962, Teor.4.1), Miranda (1978, §57) and

III.1 The Helmholtz–Weyl Decomposition of the Space L
q
149
Schechter (196 3a, 1963b); see Fujiwara & Morimo to (19 77), Simader (1990 ,
Theorem 4.1), and Simader & Sohr (1992).
4
Using the above results one can then secure the solvability of NP for
an exterior domain. To prove this, we begin to observe that, assuming at
first u ∈ C
∞
0
(Ω), the existence of a unique solution p to NP with q = 2 is
immediately established; see Remark III.1.2. One can then use the classical
estimates of Agmon, Douglis, & Nirenberg (1959 , §15) to show
p ∈ C
∞
(Ω) ∩ W
2,q
(Ω
r
), for all r > δ(Ω
c
) and all q ≥ 1. (III.1.19)
Furthermore, p solves (III.1.1 0). We shall now prove that p ∈ D
1,q
(Ω), 1 <
q < ∞, and the vali dity of (III.1 .14). To reach this goal, we take ϕ ∈ C
∞
(R)
with
ϕ(ξ) =
(
0 if |ξ| ≤ 1/2
1 if |ξ| ≥ 1
and set
ϕ
R
(x) = ϕ(|x|/R), w(x) = ϕ
R
(x)p(x), R > 2δ(Ω
c
).
From (III.1.10) we have that w solves the problem
∆w = f
f = ∇ · (p∇ϕ
R
+ uϕ
R
) + ∇ϕ
R
· (∇p − u) ≡ f
1
+ f
2
.
(III.1.20)
Clearly, f
i
∈ C
∞
0
(R
n
), i = 1 , 2. Also, by using the properties of ϕ
R
and u
along with (I II.1.10), it is readily seen that
Z
R
n
f
i
= 0, i = 1, 2, (III.1.21)
and so, by Theorem II.8. 1 (see also Remark II.8.1), f
i
∈ D
−1,q
0
(R
n
), i = 1, 2,
and we may apply the results of Exercise II.11.9(ii) and Exercise II.11.1 1 to
deduce the existence of a unique (up to a constant) solution w ∈ D
1,q
(R
n
),
1 < q < ∞, which further verifies
|w|
1,q
≤ c |f|
−1,q
, 1 < q < ∞. (II I.1.22)
From (III.1.20)
2
it follows for all ψ ∈ D
1,q
0
0
(R
n
), 1 < q
0
< ∞,
Z
R
n
f
1
ψ
≤ c
1
(kpk
q,Ω
R
+ kuk
q
) |ψ|
1,q
0
,R
n
,
where c
1
= c
1
(ϕ
R
). Furthermore, if 1 < q
0
< n, by the Sobolev inequality
(II.3.7),
4
These latter two pap ers require Ω to be only of class C
1
.

150 III The Function Spaces of Hydrodynamics
kψk
q
0
,Ω
R
≤ c
2
|ψ|
1,q
0
,R
n
,
with c
2
= c
2
(Ω
R
, q
0
). Thus, since ψ∇ϕ
R
∈ W
1,q
0
(Ω
R
), for these values of q
0
we have, for som e c
3
= c
3
(ϕ
R
),
Z
R
n
f
2
ψ
≤ c
3
k∇p −uk
−1,q,Ω
R
|ψ|
1,q
0
,R
n
.
If q
0
≥ n, we recall that the generic element of D
1,q
0
0
(R
n
) is an equivalence
class, [ψ] , constituted by functions that differ, at most, by a constant; see
(II.7.16). Thus, pick ψ ∈ [ψ] and set
ψ
0
=
1
|Ω
R
|
Z
Ω
R
ψ.
From (III.1.21), with the help of Poincar´e inequality (II.5.1 0), we deduce
Z
R
n
f
2
ψ
=
Z
R
n
f
2
(ψ − ψ
0
)
≤ c
4
k∇p − uk
−1,q,Ω
R
|ψ|
1,q
0
,R
n
= c
4
k∇p −uk
−1,q,Ω
R
|[ψ]|
1,q
0
,R
n
,
with c
4
= c
4
(ϕ
R
, Ω
R
). We may then conclude
|f|
−1,q
≤ c
5
(kuk
q
+ k∇pk
−1,q,Ω
R
+ kpk
q,Ω
R
) .
Substituting this inequality into (III.1.22) we find
|w|
1,q
≤ c
6
(kuk
q
+ k∇pk
−1,q,Ω
R
+ kpk
q,Ω
R
) .
Recalling that w = ϕ
R
p and property (III.1.19), we conclude that
p ∈ D
1,q
(Ω),
|p|
1,q ,Ω
R ≤ c
7
(kuk
q
+ k∇pk
−1,q,Ω
R
+ kpk
q,Ω
R
) ,
(III.1.23)
where c
7
= c
7
(q, n, Ω, ϕ
R
). This proves, in particular, the validity of condition
(i) of NP. Moreover,
∇p = O(|x|
−n
), |x| → ∞,
see Exercise III.1.4, and so, as in the case Ω ≡ R
n
, we show the validity of
identity (ii) of NP. The uniqueness of the solution p is likewise established,
see Exercise III.1.4. To complete the proof of the solvability of NP it remains
to extend these results to the case when u merely belongs to L
q
(Ω). To this
end, we may proceed exactly as in the case Ω ≡ R
n
(i.e., by a density argu-
ment) provided we show that the solution p just found satisfies the estimate
(III.1.14). We shall next prove that this is indeed the case. Set

III.1 The Helmholtz–Weyl Decomposition of the Space L
q
151
ψ
R
(x) = 1 − ϕ
2R
(x), v(x) = p(x)ψ
R
(x).
From (III.1.10)
1
it follows tha t the function v satisfies the following problem
in Ω
R
:
∆v = ∇ · (p∇ψ
R
+ uψ
R
) + ∇ψ
R
·(∇p − u) ≡ ∇ · U
1
+ F. (III.1.24)
Since, clearly,
Z
Ω
2R
F = 0 ,
we may employ Theorem III.3.1 (in the following section) to show the existence
of a vector field U
2
∈ W
1,q
0
(Ω
2R
) such that
∇ · U
2
= F in Ω
2R
,
kU
2
k ≤ c kF k,
with c = c(n, q, R). Setting
U = U
1
+ U
2
,
from (III.1.10)
2
and (III.1.24) we therefore obtain
∆v = ∇ · U i n Ω
2R
,
∂v
∂n
= U · n at ∂Ω
2R
.
Since Ω
2R
is bo unded (and smooth), we know that the Helmholtz–Weyl de-
composition of L
q
(Ω
2R
) holds for all values of q ∈ (1, ∞) and so, by Lemma
III.1.2 and Remark III.1.1, it follows that
|v|
1,q,Ω
2R
≤ c
1
kUk
q,Ω
2R
with c
1
= c
1
(n, q, Ω
R
). Recalling the definition of v and the estimates for
kUk
q
, we deduce
|p|
1,q,Ω
R
≤ c
2
kuk
q
+ kpk
1,q,Ω
R,2R
, (III.1.25)
where c
2
= c
2
(n, q, R, Ω
R
). Combining (III.1.23)
2
with (III.1.25) and taking
into account that problem (III.1.10) does not change if we modify p by adding
a constant to it, it follows that
|p|
1,q ,Ω
≤ c
3
kuk
q
+ k∇pk
−1,q,Ω
R
+ kpk
q,Ω
R
/R
, (III.1.26)
with
kpk
q,Ω
R
/R
≡ inf
k∈R
kp + kk
q,Ω
R
.
We claim the existence of a positive constant C = C(n, q, R, Ω
R
) such that

152 III The Function Spaces of Hydrodynamics
k∇pk
−1,q,Ω
R
+ kpk
q,Ω
R
/R
≤ Ckuk
q
. (III.1.27)
Contradicting (III.1.27) implies that there is a sequence {u
m
} ⊂ C
∞
0
(Ω) and
a sequence of corresponding solutions, {p
m
}, to (III.1.10), such tha t
ku
m
k
q
→ 0
k∇p
m
k
−1,q,Ω
R
+ kpk
q,Ω
R
/R
= 1
as m → ∞. (I II.1.28)
From (III.1.26) and (III.1.28) we obtain that
|p
m
|
1,q,Ω
≤ M , (III.1.29)
for some constant M independent of m. By the weak compactness property of
spaces
˙
D
1,q
, 1 < q < ∞ (Exercise II.6.2), we find from (III.1.2 9) the existence
of p ∈ D
1,q
(Ω) and of a subsequence {p
m
0
} such that
(∇p
m
0
, ϕ) → (∇p, ϕ) for all ϕ ∈ L
q
0
(Ω).
Thus, by this property and (ii) of NP (that we have previously established
for a ll u ∈ C
∞
(Ω)) we find for all φ ∈ D
1,q
0
(Ω)
0 = lim
m
0
→∞
(u
m
0
, ∇φ) = lim
m
0
→∞
(∇p
m
0
, ∇φ) = (∇p, ∇φ),
which, by uniqueness, in turn i mplies
∇p ≡ 0. (III.1.30)
Furthermore, from the compactness results of Exercise II. 5.7 and Theorem
II.5.3, it follows that {p
m
0
} can be chosen to converge to p i n L
q
(Ω
R
), while
∇p
m
0
tends to ∇p in W
−1,q
0
(Ω
R
). As a consequence, from (III.1.28)
2
, we find
that
k∇pk
−1,q,Ω
R
+ kpk
q,Ω
R
/R
= 1,
which contradicts (I II.1.30). Thus, (III.1.27) is established and we may con-
clude the validity of the Helmholtz–Weyl decompo sition of L
q
(Ω), 1 < q < ∞,
for a ny domain Ω of class C
2
.
We have thus proved the fol lowing theorem.
Theorem III.1.2 Let Ω ⊂ R
n
, n ≥ 2 be either a domain of class C
2
or the
whole space or a half-space. T hen the Helmholtz–Weyl decomposition holds
for L
q
(Ω), for any q ∈ (1, ∞).
5
Remark III.1.3 As already observed, in vi ew of the characterization given
in Lemma III.1.2, it is not expected that decomposition (III.1.5) holds for
arbitrary domains whenever q 6= 2 . Actually, one can show that, for certain
5
Of course, if q = 2, it holds for any Ω, see Theorem III.1.1.
III.1 The Hel mholtz–Weyl Decomposition of the Space L
q
153
smooth domains with an unbounded boundary or for bounded domains with
“sharp” corners, the Neumann problem NP loses either existence or unique-
ness for values of q in some range. This problem is analy zed in the work of
Maslennikova & Bogovski
˘
i (1986a , 1986b, 1993) and Bogovski
˘
i (1 986), where
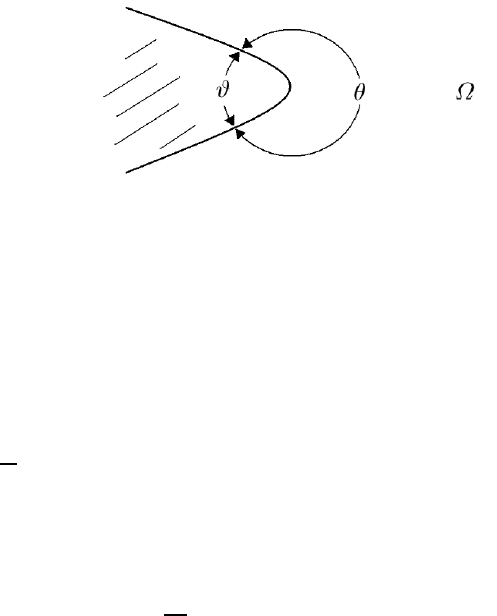
examples of such domains are given. For instance, if Ω is a domain in the
plane that i s the complement of a smoothed angle ϑ = 2π −θ < π (see Figure
III.1), then NP loses existence if
1 < q < 2/(1 + π/θ)
while it loses uniqueness if
2/(1 − π/θ) < q (III.1.31)
and therefore, for these values of q, the Helmholtz–Weyl decomposition of
L
q
(Ω) does not hol d; see also Exercise III.1.7.
Figure III.1
A counterexample to the validity of the Helmohltz-Weyl decomposition in
bounded domains with only locally Lipschitz boundary, is given in Fabes,
Mendez & Mitrea (1998, Theorem 12.2); see also the Notes for this Chapter.
For other results concerning the resolution of NP (equivalently, the va-
lidity of the Helmholtz–Weyl decomposition) in domai ns with an unbounded
boundary, we refer to the Notes for this Chapter.
Exercise III.1.4 Let p ∈ D
1,q
(Ω) be a (smooth) solution to (III.1.10) with u ∈
C
∞
0
(Ω). Show the following assertions:
(i) ∇p = O(|x|
−n
) as |x| → ∞;
(ii) If u ≡ 0, then p ≡const.
Hint: (i) Use the methods of Lemma II.9.1 to prove the relation
D
i
p(x) =
Z
∂Ω∪∂B
R
p(y)
∂
∂n
(D
i
E(x−y))dσ
y
−
n
X
j=1
Z
Ω
R
u
j
(y)D
ji
E(x−y)dy, (III.1.32)
where R is so large that Ω
R
contains the bounded support K of u. T hen let R → ∞
into (III.1.32) and employ the results of Exercise II.6.3 and the esti mate

154 III The Function Spaces of Hydrodynamics
|D
ji
E(ξ)| = O(|ξ|
−n
) as x → ∞.
(ii) Multiply (III.1.10)
1
with u ≡ 0 by p, integrate by parts over Ω
R
, use (i) and let
R → ∞.
Exercise III.1.5 We recall that a function G(x, y) is said to b e the Green’s function
for the Laplace operator in a domain Ω if G(x, y) = E(x − y) + g(x, y) with g such
that for all x ∈ Ω
∆
(y)
g(x, y) = 0 y ∈ Ω
and, moreover,
g(x, y) = −E(x − y) y ∈ ∂Ω (Dirichlet or first kind).
or
∂g(x, y)
∂n
y
= −
∂E(x −y)
∂n
y
y ∈ ∂Ω (Neumann or second kind).
Assuming Ω bounded and u and Ω sufficiently smooth, use Green’s identity (see
Lemma II.9.1) to show the following representations
u(x) =
Z
Ω
G(x, y)∆u(y)dy +
Z
∂Ω
u(y)
∂G(x, y)
∂n
y
dσ
y
(Dirichlet), (III.1.33)
u(x) =
Z
Ω
G(x, y)∆u(y)dy +
Z
∂Ω
∂u(y)
∂n
y
G(x, y)dσ
y
(Neumann). (III. 1.34)
These formulas continue to hold also if Ω is unbounded and u and G are “well
behaved” at large distances. In this connection, show that
N(x, y) ≡ E(x − y) + E(x − y
∗
), y
∗
= (y
1
, . . . , y
n−1
, −y
n
),
is Green’s function of the second kind for the half-space, while
D(x, y) ≡ E(x − y) − E(x − y
∗
) (III.1.35)
is Green’s function of the first kind and formulate assumptions on u such that
(III.1.33) and (III.1.34) are valid.
Exercise III.1.6 (Fujiwara & Morimoto 1977) Assume that Ω is such that the
Helmholtz–Weyl decomposition for L
q
(Ω) holds for all q ∈ (1, ∞). Show that the
adjoint P
∗
q
of the projection operator P
q
(see Remark III.1. 1) coincides with P
q
0
,
1/q + 1/q
0
= 1.
Exercise III.1.7 Let Ω be the “smoothed angle” domain of Figure III.1, with
θ > π. Show that the homogeneous Neumann problem (III.1.10) with u ≡ 0 has
a nonzero solution p ∈ D
1,q
(Ω), for all q satisfying (III. 1.31). Hint: Let (r, ϕ) be
a polar coordinate system w ith the origin at the tip of the “smoothed angle”. The
function
p = r
π/θ
cos
“
π
θ
ϕ
”
,
satisfies ∆p(r, ϕ) = 0 and ∂p(r, ϕ)/∂n|
∂Ω
= 0, for all (r, θ), r ≥ r
0
> 0. Moreover,
p ∈ D
1,q
(Ω
2r
0
) only for those q satisfying (III.1.31). The desired solution is then
given by p = ψ p + p
1
, where ψ = ψ(r) is 0 for r ≤ 2r
0
and is 1 for r ≥ 3r
0
, while p
1
is the unique (up to a constant) solution to the Neumann problem (III.1.10) with
u ≡ −2∇ψ · ∇p −p∆ψ, and such that ∇p
1
(r, ϕ) → 0 as r → ∞.

III.2 Relevant Properties of the Spaces H
q
and G
q
155
III.2 Relevant Properties of t he Spaces H
q
and G
q
We begin to furnish a simple characterization of elements of H
q
(Ω), 1 < q <
∞, valid for an arbitrary domain Ω. Specifically, we have
Lemma III.2.1 Let Ω be any domain in R
n
, n ≥ 2. Then, a vector field u
in L
q
(Ω), 1 < q < ∞, belongs to H
q
(Ω) if and only if
Z
Ω
u · h = 0, for all h ∈ G
q
0
(Ω). (III.2. 1)
Proof. Assume (III.2.1) holds. T hen employing the same reasoning showed
after formula (I II.1. 11), we deduce u ∈ H
q
(Ω). Conversely, take u ∈ H
q
(Ω)
and denote by {u
m
} ⊂ D(Ω) a sequence converging to u in L
q
(Ω). Integrating
by parts we show that (III.2.1) is satisfied by each u
m
and then, by continuity,
by u. ut
Relation (III.2.1) tells us, in particular, that u is w eakly divergence free,
that is,
Z
Ω
u ·∇ψ = 0, for all ψ ∈ C
∞
0
(Ω)
1
and that, in a generalized sense, the “normal component” of u at the bounda ry
is zero. Actually, if Ω is a regular bounded or exterior domain or a half-space
and u is a sufficiently smooth function of L
q
(Ω), one can show that u ∈ H
q
(Ω)
if and only if ∇ · u = 0 in Ω and u · n = 0 at ∂Ω. To this end, consider first
the case where Ω is bounded and locally Lipschitz and let u ∈ H
q
(Ω). From
the Gauss divergence theorem (see Exercise II.4.3) we have for all functions
ϕ ∈ W
1,q
0
(Ω)
Z
Ω
ϕ∇·u =
Z
∂Ω
γ(ϕ)u · n −
Z
Ω
u · ∇ϕ, (III.2.2)
where γ(ϕ) is the trace of ϕ on ∂Ω. From Lemma III.2.1 and (III.2.2) written,
in particular, with ϕ ∈ C
∞
0
(Ω) we obtain ∇ · u = 0 which, once substituted
into (III.2.2), with the aid of Lemma III. 2.1 entails
Z
∂Ω
γ(ϕ)u · n = 0, for all ϕ ∈ W
1,q
0
(Ω).
1
In analogy with the definition of the generalized derivative, one can introduce
the notion of generalized (or weak) differential operator, as in fact we already
did with the gradient operator (see also Smirnov 1964, §110). Thus, in the case
under consideration, we say that a vector u ∈ L
1
loc
(Ω) has a generalized (or weak)
divergence U ∈ L
q
loc
(Ω) if and only if
Z
Ω
u · ∇ψ = −
Z
Ω
Uψ, for all ψ ∈ C
∞
0
(Ω).
As usual, U will be denoted by ∇ · u.
