Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


6 Applications to Nonlinear PDEs in IR
N
283
6.1.4 Models from transonic gas dynamics
Quadratic operators are common in this area.
Example 6.21 (KFG equation)TheK
´
arm
´
an–Fal’kovich–Guderley (KFG) equa-
tion of transonic gas flows, [395, 504, 267],
u
t
u
tt
= u in IR
N
× IR , (6.27)
possesses exact solutions (6.26). Then p = 0andL = in the system (6.25). The
invariance of W
4
remains valid for linear perturbations of the PDE. For instance,
solutions (6.26) also satisfy the PDE
µu
ttt
+ u
t
u
tt
+ αu
t
= u in IR
N
× IR
that describe transonic flows around a thin body with effects of viscosity and heat
conductivity, for which the velocity of the gas is close to the local speed of sound,
[504]. The expansion coefficients then satisfy
6µC
4
+ 2C
2
C
3
+ αC
2
= C
1
, 4C
2
3
+ 6C
2
C
4
+ 2αC
3
= C
2
,
18C
3
C
4
+ 3αC
4
= C
3
, 18C
2
4
= C
4
.
Example 6.22 (LRT equation) Next, considerthe Lin–Reissner–Tsien (LRT) equa-
tion [395]
2u
xt
+ u
x
u
xx
= u
yy
in IR
2
× IR , (6.28)
which plays an important role as a simplified equation of gas motion at sonic ve-
locities in a channel (nozzle) with the plane geometry. It is derived by the so-called
transonic expansion using small deviations from unity of the actual Mach number of
the flow; see also [504, 133] and further comments below.
First of all, using the invariant subspace W
4
= L{1, x, x
2
, x
3
} of u
x
u
xx
(a mod-
ule), we find
u(x , y, t) = C
1
(y, t) + C
2
(y, t)x + C
3
(y, t)x
2
+ C
4
(y, t)x
3
, (6.29)
where the coefficients satisfy the PDE system
C
2t
=
1
2
C
1yy
− C
2
C
3
,
C
3t
=
1
4
C
2yy
− C
2
3
−
3
2
C
2
C
4
,
C
4t
=
1
6
C
3yy
− 3C
3
C
4
,
0 = C
4yy
− 18C
2
4
.
As happened a few times before, the last ODE is independent of the others and
represents a classical semilinear elliptic equation from combustion theory (t is a
parameter). Once C
4
(y, t) is known, the rest of the equations can be solved step by
step, as with usual ODEs for C
3
, C
2
,andC
1
.
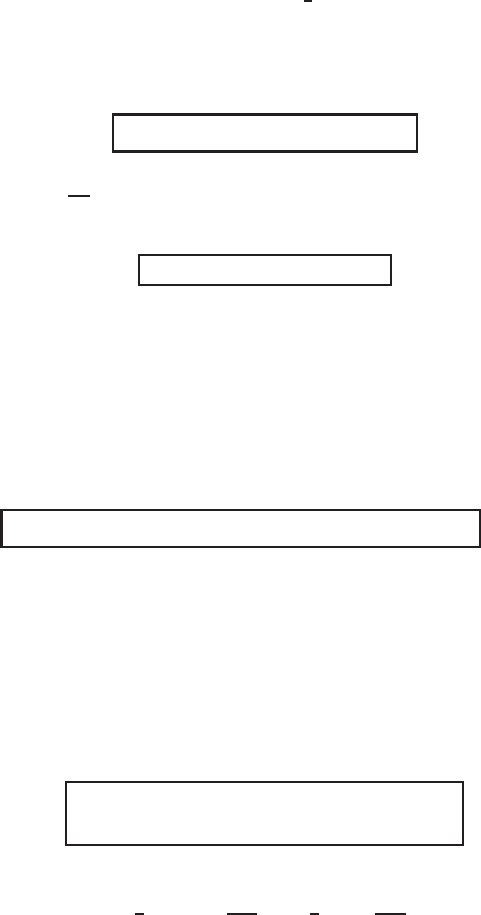
Secondly,concerningsimplerreductionsof the LRT equation,there exist solutions
of (6.28) on W
7
= L{1, x , x
2
, y, y
2
, xy, xy
2
},
u(x , y, t) = C
1
+ C
2
x + C
3
x
2
+ C
4
y + C
5
y
2
+ C
6
xy + C
7
xy
2
, (6.30)
© 2007 by Taylor & Francis Group, LLC
284 Exact Solutions and Invariant Subspaces
C
2
=−C
2
C
3
+ C
5
,
C
3
=−C
2
3
+
1
2
C
7
,
C
6
=−C
3
C
6
,
C
7
=−C
3
C
7
.
The same low-dimensional reductions apply to the complete version of the LRT
equation
2u
xt
−
K − (γ +1)u
x
u
xx
= u
yy
, (6.31)
where γ is the adiabatic exponent of the gas and K ∼ 1 − M
2
∞
, with the Mach
number M
∞
=
U
a
∞
, a
∞
and U being the characteristic velocity of sound and the
velocity of main flow in the channel respectively. The viscosity version of the LRT
equation [504]
2u
xt
− µu
xxx
+ u
x
u
xx
= u (6.32)
also possesses such exact solutions.
The Ryzhov–Khristianovitch equations (or “short waves” equations) [504] be-
long to the same class of models,
u
y
− 2v
t
− 2(v − x)v
x
− 2kv = 0,
v
y
+ u
x
= 0,
where (u,v) is the velocity field, and k = 0 or 1 for plane or axisymmetric waves
respectively. In the potential form with u = w
y
, v =−w
x
, the system reduces to the
single equation
2w
tx
− 2(x +w
x
)w
xx
+ 2kw
x
+ w
yy
= 0inIR
2
× IR , (6.33)
possessing solutions (6.29) and (6.30) with similar DSs.
Example 6.23 (Full model of potential flows) Finally, we treat the full model of
potential transonic flow, where the shock waves (if any) remain weak, the flow vor-
ticity is low, and hence, the velocity potential can be introduced by
u =
x
,
v =
y
.
The PDE for follows from the equations of motion and continuity (see Guderley
[267, p. 7] and [133])
tt
+ 2
x
xt
+ 2
y
yt
=
a
2
− (
x
)
2
xx
−2
x
y
xy
+
a
2
− (
y
)
2
yy
,
(6.34)
where the velocity of sound a is determined by the equation of the conservation of
energy
t
+
1
2
|∇|
2
+
1
γ −1
a
2
=
1
2
U
2
+
1
γ −1
a
2
∞
. (6.35)
In particular, the complete LRT equation (6.31) is derived from this system by ex-
pansion of the potential under the assumptions that M
∞
≈ 1 in a special {x, y}-
geometry corresponding, e.g., to the plane or circular (where u
yy
is replaced by
u
yy
+ u
zz
) Laval nozzle, [133, 267].
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
285
Consider the full system and substitute a
2
from (6.35),
a
2
= a
2
∗
− (γ − 1)
t
−
γ −1
2
|∇|
2
, with a
2
∗
= a
2
∞
+
γ −1
2
U
2
,
into (6.34). In this case, the resulting quadratic and cubic operators on the left- and
right-hand sides admit W
4
= L{1, x
2
, xy, y
2
} (for simplicity, we do not include the
subspace of linear functions L{x, y} that gives new solutions),
(x, y, t) = C
1
(t) + C
2
(t)x
2
+ C
3
(t)xy + C
4
(t)y
2
,
C
1
+ 2(γ − 1)(C
2
+ C
4
)C
1
= 2a
2
∗
(C
2
+ C
4
),
C
2
+ 2[(γ + 3)C
2
+ (γ −1)C
4
]C
2
+ 2C
3
C
3
=−4(γ + 1)C
3
2
−(γ + 3)C
2
C
2
3
− 4(γ − 1)C
2
2
C
4
− (γ + 1)C
2
3
C
4
,
C
3
+ 4C
3
C
2
+ 2(γ + 1)(C
2
+ C
4
)C
3
+ 4C
3
C
4
=−4(γ + 1)
C
2
2
+ C
2
4
C
3
− 8γ C
2
C
3
C
4
− 2C
3
3
,
C
4
+ 2C
3
C
3
+ 2[(γ − 1)C
2
+ (γ +3)C
4
]C
4
=−(γ + 1)C
2
C
2
3
−4(γ − 1)C
2
C
2
4
− (γ +3)C
2
3
C
4
− 4(γ + 1)C
3
4
.
6.1.5 Maxwell equations in nonlinear optics
We consider the model [254], consisting of Maxwell equations coupled to a sin-
gle Lorentz oscillator governing the polarization field P, in which the oscillator is
driven by the electric field E. Assuming a transverse plane wave propagating along
the z-axis with E = (E(z, t), 0, 0)
T
, displacement current D = (D(z, t), 0, 0)
T
,
polarization P = (P(z, t), 0, 0)
T
all along the x -axis, and the magnetic field induc-
tion B = (0, B(z, t), 0)
T
along the y-axis, Faraday’s law and the Amp
`
ere equation,
together with the Lorentz oscillator equation, can be written as
B
t
+ E
z
= 0,
D
t
+ B
z
= 0,
P
tt
+ P − αE = 0.
(6.36)
Here the displacement current
D = E +
1
2k+1
E
2k+1
, with k = 1or2,
depends in a nonlinear manner on the electric field. The coupling parameter α in the
Lorentz equation ensures that the polarization oscillations are driven by the electric
field E.Inviewofthefirst PDE in (6.36), introducing the potential u = u(z, t) by
B = u
z
,
E =−u
t
,
reduces the system to two PDEs
−u
t
−
1
2k+1
(u
t
)
2k+1
t
+ u
zz
= 0,
P
tt
+ P + αu
t
= 0.
© 2007 by Taylor & Francis Group, LLC
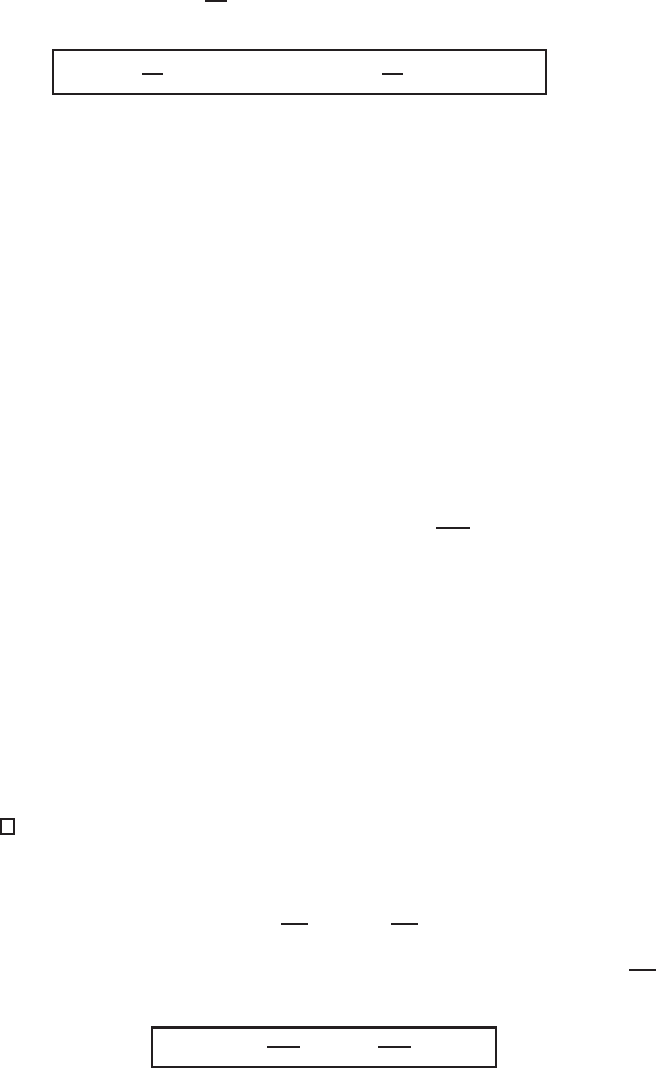
286 Exact Solutions and Invariant Subspaces
Finally, applying operator
d
2
dt
2
+ I to the first equation and using the second yields
the following quasilinear wave equation in IR × IR
+
[572]:
F
k
[u] ≡
d
2
dt
2
+ I
1 + (u
t
)
2k
u
tt
=
d
2
dt
2
+ I
u
zz
− αu
tt
. (6.37)
For k = 1, the quadratic operator F
1
[u] admits L{1, t, t
2
}, so (6.37) possesses
u(z, t) = C
1
(z) + C
2
(z)t + C
3
(z)t
2
,
C
1
= 2(1 + C
2
2
)C
3
+ 2αC
3
,
C
2
= 8C
2
C
2
3
,
C
3
= 8C
3
3
.
6.2 Extended invariant subspaces for second-order operators
6.2.1 Fourth-degree radial polynomial subspaces
Let us return to general quadratic operators (6.1) and first look for an extension of
the standard polynomial subspaces listed in Proposition 6.1. Consider the following
simple extension result in the class of radially symmetric functions.
Proposition 6.24
Operator
(6.1)
preserves the 3D subspace
W
r
3
= L{1, |x|
2
, |x |
4
}
iff
γ =−
N+2
4
β. (6.38)
Proof. Setting
u = C
1
+ C
2
|x|
2
+ C
3
|x|
4
(6.39)
and using equalities |x|
2
= 2N , |x|
4
= 4(N +2)|x|
2
,wefind that
F[u] =
1
+
2
|x|
2
+
3
|x|
4
+ 4C
2
3
[(N + 2)β + 4γ ]|x |
6
, (6.40)
so always F[u] ∈ W
r
3
iff (N + 2)β + 4γ = 0. The expansion coefficients are
1
= 2β NC
1
C
2
+ 4αN
2
C
2
2
,
2
= 4β(N + 2)C
1
C
3
+ 16α N(N + 2)C
2
C
3
+ β(N − 2)C
2
2
,
3
= 2β NC
2
C
3
+ 16α(N +2)
2
C
2
3
.
Example 6.25 (Blow-up for fast diffusion equation with source) Consider posi-
tive solutions of the following fast diffusion equation with source:
v
t
=∇·
v
−
4
N+2
∇v
+ bv
N+6
N+2
+ cv, (6.41)
where b > 0andc > 0 are constants. Using the pressure transformation u = v
−
4
N+2
yields the quasilinear heat equation with absorption
u
t
= uu −
N+2
4
|∇u|
2
−
4
N+2
(b + cu), (6.42)
© 2007 by Taylor & Francis Group, LLC
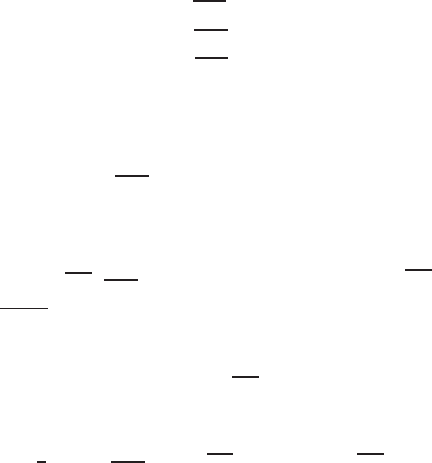
6 Applications to Nonlinear PDEs in IR
N
287
where the quadratic operator admits the subspace in (6.38). Hence, there exist solu-
tions (6.39), where the expansion coefficients solve the DS
C
1
=
1
−
4
N+2
(b +cC
1
),
C
2
=
2
−
4
N+2
cC
2
,
C
3
=
3
−
4
N+2
cC
3
.
The quenching behavior for (6.42), where u → 0ast → T
−
, is equivalent to blow-
up for the original PDE (6.41). The asymptotic setting is similar to that for the TFE
in Section 3.2 and is easier. Let b = 1andc = 0 in (6.41). Estimating
C
1
(t) =
4
N+2
(T − t) + ... as t → T
−
from the first ODE, and taking any orbit such that C
2
(t) → a
0
> 0andC
3
(t) → a
1
as t → T , we obtain the following blow-up pattern for (6.41):
v(x , t) = (T − t)
−
N+2
4
4
N+2
1 + a
0
|ξ|
2
+ a
1
e
−τ
|ξ|
4
+ ...
−
N+2
4
, (6.43)
where ξ = r/
√
T − t and τ =−ln(T − t) are the new variables. According to
(6.43), let us introduce the rescaled function
v(x , t) = (T − t)
−
N+2
4
w(ξ, τ)
satisfying the singular perturbed first-order PDE
w
τ
=−
1
2
w
ξ
ξ −
N+2
4
w + w
N+6
N+2
+ e
−τ
∇·
w
−
4
N+2
∇w
. (6.44)
The passage to the limit as τ →∞in (6.44) uses specific stability techniques; see
[245, Ch. 5]. Recalling that {u = 0}={v =+∞}for nonnegative solutions u(x, t),
the extinction behavior as t → T
−
of compactly supported solutions of (6.42) de-
scribes the evolution and finite-time focusing of the burnt zone {v =+∞}of blow-
up solutions v(x, t), which are now the minimal proper solutions of (6.41) uniquely
constructed by a monotone approximation (a truncation) of the PDE. FBP theory for
such blow-up solutions is developed for the second-order parabolic problems, [226,
Ch. 5]. Notice an interesting feature: the blow-up interfaces r = s(t) are not C
2
smooth for t > 0ands
(t) is not more than Lipschitz continuous, [226, p. 140].
We next perform an extension of the invariant subspace (6.38).
Proposition 6.26
If the condition in
(6.38)
holds, operator
(6.1)
admits
L{W
q
n
, |x |
4
}, (6.45)
where
W
q
n
is the subspace
(6.5)
with general quadratic forms in
IR
N
.
Proof. Take an arbitrary function on the subspace (6.45),
u(x , t) = C(t) + x
T
A(t) x + G(t)|x|
4
, so (6.46)
u = 2(tr A) + 4(N + 2)G|x |
2
, |∇u|
2
= 4
(l)
( j )
a
l, j
x
j
+ 2G|x |
2
x
l
2
,
F[u] = 4α(tr A)
2
+ 2β(tr A) C + 4(N + 2)
4α(tr A) + βC
G|x|
2
+2β(tr A)x
T
Ax+ 4γ x
T
A
2
x + 2
8α(N + 2)
2
G + β(tr A)
G|x|
4
+ S.
© 2007 by Taylor & Francis Group, LLC

288 Exact Solutions and Invariant Subspaces
Here, S denotes the fourth and sixth-degree polynomials,
S = 4[β(N +2) + 4γ ]
|x|
2
x
T
Ax+ G|x|
6
G,
which, in general, do not belong to the subspace. S vanishes due to the condition in
(6.38).
Example 6.27 (Hyperbolic equation) The formally hyperbolic equation
u
tt
= F[u] ≡ α(u)
2
+ βuu −
N+2
4
β|∇u|
2
in IR
N
× IR
on the subspace (6.45) reduces to the DS for the coefficients of expansion (6.46),
C
= 4α(tr A)
2
+ 2β(tr A)C,
A
= 2β(tr A) A − (N +2)A
2
+ 4(N +2)
4α(tr A) + βC
I
N
,
G
= 16α(N + 2)
2
G
2
+ 2βG(tr A).
In the case of diagonalquadratic forms as in (6.4),the computationsare easier and
subspace L{W
q
N+1
, |x |
4
} remains invariant. In fact, this is the generic case, since,
by an orthogonal transformation x → Px ( and |∇(·)|
2
are invariant), x
T
Ax is
reduced to a diagonal form, while the canonical form |x|
2
, and hence |x|
4
, remain
unchanged. On the other hand, it seems that, in this case, we cannot add linear func-
tions (6.2) to the invariant subspace. Indeed, translations in IR
N
split |x |
4
into a
number of terms, including a cubic form, such as
b
i, j
x
2
i
x
j
, which is not invariant.
More general quartic forms, such as
b
i, j
x
2
i
x
2
j
, do not also lead to invariant sub-
spaces (unless they reduce to radial function |x|
4
for b
i, j
= 1). Recall in this context
that the actual dimension of the spaces of exact solutions is determined by the order
of the correspondingDS for the expansion coefficients, i.e., depends on the evolution
order (the highest time-derivative) of the PDE.
Example 6.28 (On non-symmetric blow-up) Using solutions (6.46) makes it pos-
sibleto describe non-symmetricblow-upand non-radialblow-upinterfacesfor (6.41)
with b = 1andc = 0. The simpler case G(t) ≡ 0 has been studied in detail, [226,
p. 152]. As a result, it was shown that blow-up analytic interfaces in general are not
the proper ones for minimal solutionsthat have finite regularity. For general blow-up
solutions, a fully developed mathematical regularity theory of singular interfaces is
still absent. It would be interesting to extend some of the results on non-symmetric
blow-up interfaces in the corresponding wave PDEs, such as
u
tt
= uu −
N+2
4
|∇u|
2
−
4
N+2
(b + cu),
using similar exact solutions. These give several OPEN PROBLEMS.
6.2.2 Logarithmic perturbation of quadratic polynomials
Here,a specialexampleof non-autonomousquadraticoperatorsand ODEs governing
the invariant subspaces is considered.
Critical fast diffusion equation and invariant subspace. We begin with a parabolic
© 2007 by Taylor & Francis Group, LLC
6 Applications to Nonlinear PDEs in IR
N
289
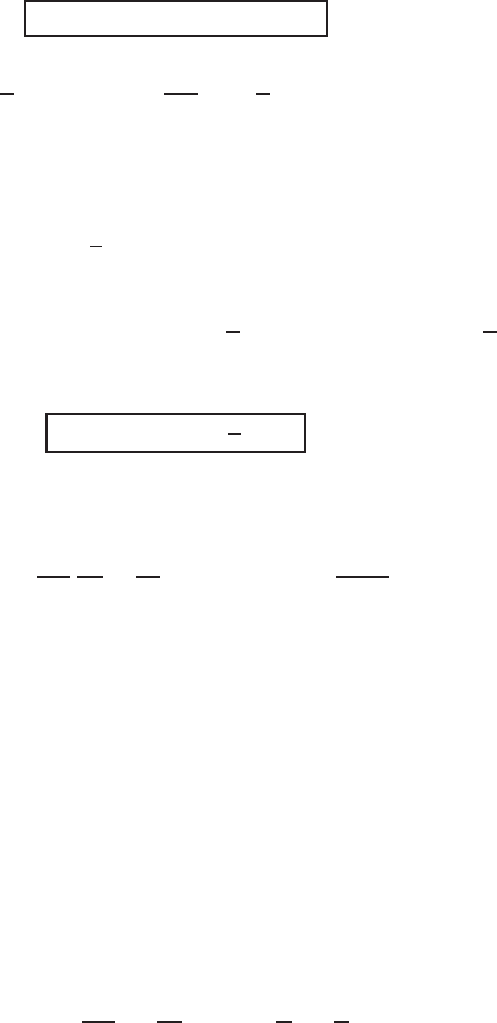
PDE in a radially symmetric case,
u
t
= F[u] + [u]inIR
N
× IR
+
, (6.47)
where F is the quadratic operator
F[u] = uu −
N
2
|∇u|
2
≡ u
u
rr
+
N−1
r
u
r
−
N
2
(u
r
)
2
, with r =|x| > 0,
and is a linear lower-order operator, including a convection-like term,
[v] = β(x ·∇v) + γv ≡ βr v
r
+ γv.
The quasilinear operator F occurs in the fast diffusion equation with another critical
exponent
v
t
=∇·
v
−
2
N
∇v
in IR
N
× IR
+
(N ≥ 3). (6.48)
This is a famous equation in diffusiontheory. The asymptotic behavior of its positive
L
1
-solutions is complicated and inherits certain features of similarity solutions for
the diffusivity coefficient v
σ
of the first (σ>−
2
N
)andthesecond kind (σ<−
2
N
).
This represents an important example of the matched asymptotics; see details, ref-
erences, and discussion in [245, Ch. 5]. The pressure transformation v
−2/N
= u
reduces (6.48) to
u
t
= F[u] ≡ uu −
N
2
|∇u|
2
.
It turns out that, in the so-called outer region (i.e., sufficiently remote from the origin
x = 0), the asymptotic behavior of finite mass solutions can be described by special
orbits belonging to a peculiar subspace W
2
= L{|x|
2
, |x |
2
ln|x |} invariant under F.
Such radial self-similar solutions are
v(x , t) =
1
N−2
|x |
2
t
ln
|x |
at
γ
∈ W
2
, with γ =
N
2(N−2)
,
where a > 0 is arbitrary. The solutions are positively defined in {|x | > at
γ
} and
correctly describe the outer asymptotic behavior governedby a singular perturbation
of a first-order conservation law. This is a key feature of such a matched asymptotic
structure.
The outer behaviorshowsthat the evolution on the invariantsubspace W
2
is stable,
in the sense that it attracts a wide set of other general non-invariant orbits, [245,
Theorem 6.3]. The internal structure of W
2
plays a role. In particular, it is important
that
W
2
= L{|x |
2
}⊕L{|x|
2
ln|x|},
where the first 1D subspace is also invariant under F, while the second one is not.
Moreover, in rigorous mathematical analysis of the asymptotic behavior, it is proved
that, in the outer region, evolution orbits move towards the second (non-invariant)
subspace.
Let us now state a simple invariant property of operators F and .
Proposition 6.29
Both operators
F
and
admit subspace
W
2
= L{r
2
, r
2
lnr }
given by the linear homogeneous elliptic PDE with non-constant coefficients
u − (N +2)
x·∇u
|x |
2
+ 4
u
|x |
2
≡ u
rr
− 3
u
r
r
+ 4
u
r
2
= 0.
© 2007 by Taylor & Francis Group, LLC
290 Exact Solutions and Invariant Subspaces
We derive the corresponding exact solutions of the general evolution PDE
P(
∂
∂t
)[u] = F[u] +[u], (6.49)
where P(
∂
∂t
) is a linear polynomial operator with coefficients, depending on t only.
Corollary 6.30
The PDE
(6.49)
on
W
2
with
u(x , t) = C
1
(t)|x |
2
+ C
2
(t)|x |
2
ln|x|
is the DS
P[C
1
] = (2 − N)C
1
C
2
−
N
2
C
2
2
+ (2β + γ)C
1
+ βC
2
,
P[C
2
] = (2 − N)C
2
2
+ (2β + γ)C
2
.
In particular, for (6.47), the following holds:
C
1
= (2 − N)C
1
C
2
−
N
2
C
2
2
+ (2β + γ)C
1
+ βC
2
,
C
2
= (2 − N)C
2
2
+ (2β + γ)C
2
.
In the case of the hyperbolic Boussinesq-type equation
u
tt
= F[u] + [u],
the DS is of fourth order with C
1,2
replaced by C
1,2
.
Reduction to the autonomous operator and ODE. For convenience, replacing r
by x and u by y as in Section 2.1, yields the quadratic operator
F[y] = y
y
+
N−1
x
y
−
N
2
(y
)
2
,
while the subspace W
2
is given by Euler’s ODE
y
−
3y
x
+
4y
x
2
= 0.
Both are not autonomous relative to the space variable x. Observing that, on W
2
,the
operator F is equivalent to the first-order one
F[y] ≡−
N
2
(y
)
2
+
3
x
yy
−
4
x
2
y
2
,
we use the transformation
y = e
2˜x
˜y ≡ x
2
˜y, x = e
˜x
,
yielding the autonomous quadratic operator
˜
F[˜y] =
1
x
2
F[y] =˜y ˜y
−
N
2
( ˜y
)
2
+ (2 − N) ˜y ˜y
.
Then the invariant subspace consists of linear functions,
˜y ∈
˜
W
2
= e
−2˜x
L
x
2
, x
2
ln x}=L{1, ˜x
.
This operator and the corresponding subspace are described in Section 2.5.2.
It is easy to present a more general set of fully nonlinear second-order operators
preserving subspace W
2
, e.g.,
˜
F[˜y] = G( ˜y, ˜y
, ˜y
) + α( ˜y
)
2
+ β ˜y ˜y
,
where G is an arbitrary function satisfying G(a, b, 0) ≡ 0.
© 2007 by Taylor & Francis Group, LLC
6 Applications to Nonlinear PDEs in IR
N
291
6.2.3 Polynomial-exponential subspaces
Example 6.31 (Quasilinear heat equation) Consider the quasilinear heat equation
with absorption or source
v
t
= (v
σ
v
x
)
x
− γv
σ +1
, where γ =
4(σ +1)
σ
2
(σ = 0). (6.50)
Let σ>−1, i.e., γ>0. In this case, as shown in Section 1.5, there exist solutions
on the 3D exponential subspace
v
σ
∈ W
3
= L{1, cosh2x, sinh 2x } (6.51)
(for γ<0, a subspace of trigonometric functions occurs). By the transformation
x = lnr,
v
σ
=
1
r
2
u
σ
,
(6.50) reduces to the quasilinear purely diffusive equation in radial geometry,
u
t
=∇
r
·
u
σ
∇
r
u
≡
1
r
N−1
r
N−1
u
σ
u
r
r
in IR
N
× IR
+
, (6.52)
with dimension N =−
2(σ +2)
σ
which is not necessarily an integer and is negative
for σ>0. It follows from (6.51) that (6.52) admits exact solutions on the following
subspace:
u
σ
≡ r
2
v
σ
∈
ˆ
W
3
= L
r
2
, r
2
cosh(2lnr ), r
2
sinh(2lnr)
.
Similar to Example 1.15, for σ =−
4
3
, there exists the 5D subspace
ˆ
W
5
= L
r
2
, r
2
cosh(2lnr), r
2
sinh(2lnr), r
2
cosh(4lnr), r
2
sinh(4lnr)
.
6.2.4 Singular subspaces for the critical diffusion exponent
Proposition 6.32
The quadratic diffusion operator
F
∗
[u] = uu + γ
∗
|∇u|
2
,
with
γ
∗
=−
N−4
2(N−3)
, N = 3,
admits the subspace
W
s
= L
|x|
2
, |x |
4−N
, |x |
6−2N
. (6.53)
The subspace W
s
is 3D, exceptin the case of N = 2, where it is 1D with γ
∗
=−1,
corresponding to the remarkable operator to be studied in detail in the next section.
For N = 1, we have γ
∗
=−
3
4
,andW
s
= L{x, x
2
, x
3
} is indeed a subspace of
the more general 5D one, W
5
= L{1, x, x
2
, x
3
, x
4
}, described in Example 1.14. For
N ≥ 4, the subspace contains a singular function at the origin, e.g.,
W
s
= L
1, |x |
2
, |x |
−2
for N = 4. (6.54)
Example 6.33 (Fast diffusion equation) Consider the PDE
v
t
=∇·
v
−
2(N −3)
N−4
∇v
for N > 4.
The pressure u = v
−
2(N −3)
N−4
satisfies the equation u
t
= F
∗
[u]. Therefore, there exist
© 2007 by Taylor & Francis Group, LLC

292 Exact Solutions and Invariant Subspaces
solutions on the subspace (6.53),
u(x , t) = C
1
(t)r
2
+ C
2
(t)r
4−N
+ C
3
(t)r
6−2N
,
C
1
=
2(N−2)
2
N−3
C
2
1
,
C
2
=
2(N−2)
2
N−3
C
1
C
2
,
C
3
= (N − 2)
2
2C
1
C
3
−
N−4
2(N−3)
C
2
2
.
Similarly, exact solutions u = v
σ
∗
∈ W
3
exist for the hyperbolic PDE
v
1−σ
∗
(v
σ
∗
)
tt
=∇·(v
σ
∗
∇v), with σ
∗
=
1
γ
∗
.
Example 6.34 (Quenching on a sphere) The quasilinear degenerate heat equation
with constant absorption
u
t
= uu − 1inIR
4
× IR
+
has solutions on the subspace (6.54),
u(x , t) = C
1
(t)r
2
+ C
2
(t) + C
3
(t)r
−2
, (6.55)
C
1
= 8C
2
1
,
C
2
= 8C
1
C
2
− 1,
C
3
= 8C
1
C
3
.
Integrating yields the explicit solution
u(x , t) =−
1
8t
|x|
2
+
B
t
−
1
2
t +
A
8t
|x|
−2
(A, B ∈ IR ).
Here, u(x , t) is always unbounded at the origin x = 0, showing that such singular
solutions can be global in time. Taking positive initial data C
k
(0)>0, due to the
absorption term −1 in the second ODE, the solution may vanish in finite time, as
t → T
−
, at some point r = r
0
> 0. This is quenching on a sphere {|x|=r
0
} (not a
standard single point quenching), which is a subject of asymptotic singularity theory
for the PME-type equations, [245, Ch. 5]. Here we detect such behavior via explicit
formulae; see Figure 6.1. For t > T , an FBP appears with two moving interfaces at
r = s
±
(t).
In a similar manner, extinction phenomenon on W
3
can be described for the de-
generate quadratic wave equation with absorption
u
tt
= uu − 1inIR
4
× IR
+
.
6.2.5 On a cubic operator in IR
N
Proposition 6.35
The cubic operator in
IR
N
F[u] = u
2
u −
N
2
u|∇u|
2
admits
W
r
2
= L{1, |x |
2
}.
Example 6.36 (Fast diffusion equation in IR
N
) Setting v = u
−
N+2
2
(v is not the
pressure!) in the fast diffusion equation with critical exponents
v
t
=∇·
v
−
4
N+2
∇v
−
N+2
2
av + bv
N+4
N+2
(6.56)
© 2007 by Taylor & Francis Group, LLC
