Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter

Подождите немного. Документ загружается.

116 9 Supercurrents and Flux Quantization

than for high-v

materials, in agreement with experimental evidence. For example

high-T

superconductors have high B

, reﬂecting the fact that they have low pairon

speeds (c

≡ v

( j)

/2 ∼ 10

−1

). Since the supercurrent itself induces a mag-

netic ﬁeld, there is a limit on the magnitude of the supercurrent, called a critical

current.

Problem 9.1.1. Apply Equation (9.7) to the ring supercurrent and show that γ =

0. Note: The phase γ does not depend on the quantum number n, suggesting a

general applicability to the Bohr–Sommerfeld quantization rule with a high quantum

number.

9.2 Phase of the Quasi-Wavefunction

The supercurrent at a small section along the ring is represented by

⌿

(x) = A exp(ipx/), (9.9)

where A is a constant amplitude. We put q

≡ p; the pairon momentum is denoted

by the more conventional symbol p. The quasi-wavefunction ⌿

in Equation (9.9)

represents a system-state of pairons all condensed at p and the wavefunction ψ

in Equation (9.3) the single-pairon state. ⌿

and ψ

are the same function except

for the normalization constant (A). In this chapter we are mainly interested in the

supercondensate quasi-wavefunction. We simply call ⌿ the wavefunction hereafter

(omitting quasi). In a SQUID shown in Fig. 1.8 two supercurrents macroscopi-

cally separated (∼ 1 mm) can interfere just as two laser beams coming from the

same source. In wave optics two waves are said to be coherent if they can inter-

fere. Using this terminology, two supercurrents are coherent within the coherence

range of 1 mm. The coherence of the wave traveling through a region means that if

we know the phase and amplitude at any space-time point, we can calculate the

same at any other point from a knowledge of the k-vector (k) and angular fre-

quency (ω). In the present section we discuss the phase of a general wavefunction

and obtain an expression for the phase difference at two space-time points in the

superconductor.

First consider a monochromatic plane wave running in the x-direction

⌿ = Ae

i2π(x/λ−t/T )

= Ae

i(px−Et)/

, (9.10)

where the conventional notations: 2π/λ ≡ k,2π/T ≡ ω, p ≡ k, E ≡ ω are

used. We now take two points (r

, t

, r

, t

). The phase difference (δφ)

between

them,

(⌬φ)

= k(x

− x

) −ω(t

−t

), (9.11)

9.2 Phase of the Quasi-Wavefunction 117

depends on the time difference t

−t

only. In the steady-state condition, ω(t

−t

)

is a constant, which will be omitted hereafter. The positional phase difference is

(⌬φ)

≡ φ(r

) −φ(r

) = k(x

− x

). (9.12)

The phase-diffrence δφ for a plane wave proceeding in a k direction is given by

(⌬φ)



→r

k ·dr, (9.13)

where the integration is along a directed straight line path from r

to r

. When

the plane wave extends over the whole space, the line integral

(

→r

k · dr,

along any curved path joining the points (r

, r

), see Fig. 9.2, has the same value

(Problem 9.2.1):

(⌬φ)

≡



→r

k ·dr =



k ·dr. (9.14)

The line integral now depends on the end points only, and it will be denoted by

writing out the limits explicitly as indicated in the last member of Equation (9.14).

The same property can equivalently be expressed by (Problem 9.2.2)

k ·dr = 0, (9.15)

where the integration is carried out along any closed directed path C.

We consider a ring supercurrent as shown in Fig. 9.3 (a). For a small section, the

enlarged section containing point A, see (b), the supercurrent can be represented by

a plane wave having the momentum p = k. The phase difference (⌬φ)

, where

, r

) are any two points in the section, can be represented by Equation (9.14). If

we choose a closed path ABA, the line integral vanishes:

(⌬φ)

ABC

k ·dr = 0. (9.16)

Fig. 9.2 Directed paths from

to r

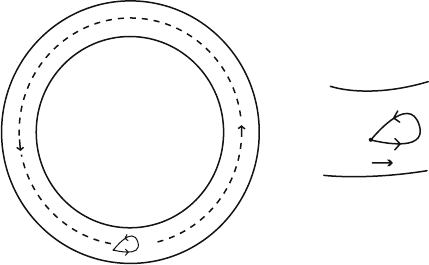
118 9 Supercurrents and Flux Quantization

(a)

(b)

Enlarged

Fig. 9.3 (a) A ring supercurrent; (b) an enlarged section

Let us now calculate the line integral along the ring circumference ARA indicated

by the dotted line in (a). Note: The vector k changes its direction along the ring; for

each small section, we may use Equation (9.14). Summing over all sections, we

obtain

(⌬φ)

ARA

k ·dr = kL, (9.17)

where L is the ring length. Thus the line integral along the closed path ARA does not

vanish. In fact if we choose a closed path C that circles the cavity counterclockwise

times and clockwise N

times, the integral along the closed path is

(⌬φ)

k ·dr = (N

− N

)kL. (9.18)

Cases ABA [ARA], represented by Equation (9.16) [(9.17)] can be obtained from

this general formula by setting N

= N

= 0(N

= 1, N

= 0). Since the

momentum p ≡ k is quantized such that p

= 2n/L, Equation (9.18) can be

re-expressed as

(⌬φ)

k ·dr = 2π(N

− N

)n. (9.19)

Problem 9.2.1. (a) Calculate the line integral in Equation (9.14) by assuming a

straight path from r

to r

, and verify the equivalence of Equations (9.14) and (9.15).

(b) Assume that the path is composed of two straight paths. Verify the equivalence.

Problem 9.2.2. (a) Assume Equation (9.14) and verify Equation (9.15). (b) Prove

the inverse: assume Equation (9.15) and verify Equation (9.14).

9.3 London’s Equation: Penetration Depth 119

9.3 London’s Equation: Penetration Depth

In 1935 the brothers F. and H. London published a classic paper [8, 9] on the elec-

trodynamics of a superconductor. By using London’s equation (9.30) together with

Maxwell’s equation (9.37), they demonstrated that an applied magnetic ﬁeld B does

not drop to zero abruptly inside the superconductor but penetrates to a certain depth.

In this section we derive London’s equation and its generalization. We also discuss

ﬂux quantization once more.

In Hamiltonian mechanics the effect of electromagnetic ﬁelds (E, B) is included

by replacing the Hamiltonian without the ﬁelds, H(r, p), with



= H(r, p −qA) +q⌽, (q = charge) (9.20)

where (A,φ) are the vector and scalar potentials generating the electromagnetic

ﬁelds:

B =∇×A, E =−∇φ −

⭸A

⭸t

, (9.21)

and then use Hamilton’s equations of motion. In quantum mechanics we may use

the same Hamiltonian H



(the prime dropped hereafter) as a linear operator and

generate Schr

odinger’s equation of motion. Detailed calculations show (Problem

9.3.1) that the phase difference (⌬φ)

changes in the presence of the magnetic

ﬁeld such that

(⌬φ)





p ·dr +





A ·dr ≡ (⌬φ)

(motion)

+(⌬φ)

(B)

. (9.22)

We call the ﬁrst term on the rhs the phase difference due to the particle motion

and the second term, the phase difference due to the magnetic ﬁeld. [The motion of

charged particles generates an electric current, so (⌬φ)

(motion)

mayalsobereferred

to as the phase difference due to the current.]

We now make a historical digression. Following London–London [8, 9], let us

assume that the supercurrent is generated by hypothetical superelectrons. A super-

electron has mass m and charge −e. Its momentum p is related to its velocity v

v = p/m. (9.23)

The supercurrent density j

is then

=−en

v. (9.24)

120 9 Supercurrents and Flux Quantization

Using the last two equations we calculate the motional phase difference:

(⌬φ)

(motion)

≡





p ·dr =−





en



·dr. (9.25)

Let us consider an inﬁnite homogeneous medium, for which the line-integral of

the phase along any closed path vanishes [see Equation (9.15)]





·dr = 0. (9.26)

Employing Stoke’s theorem (Problem 9.3.2)

dr ·C =



dS ·∇×C, (9.27)

where the rhs is a surface integral with differential element dS pointing in a direction

according to the right-hand screw rule, we obtain from Equation (9.26)

−1

A +∇χ = 0, (9.28)

where χ(r) is an arbitrary scalar ﬁeld. Now, the connection between the magnetic

ﬁeld B and the vector potential A, as represented by B =∇×A, has a certain

arbitrariness; we may add the gradient of the scalar ﬁeld χ to the original vector

ﬁeld A since

∇×(A +∇χ ) =∇×A. (9.29)

Using this gauge-choice property we may rewrite Equation (9.28) as

=−e

−1

A ≡−⌳

A, ⌳

≡ e

−1

. (9.30)

This is known as London’s equation. The negative sign indicates that the super-

current is diamagnetic. The physical signiﬁcance of Equation (9.30) will be dis-

cussed later.

Let us go back to the condensed pairon picture of the supercurrent. First, consider

a +pairon having charge +2e. Since the pairon has the linear energy-momentum

relation.



= w

+(1/2)v

(2)

p ≡ w

p, (9.31)

the velocity v

has magnitude c

≡ v

(2)

/2 and direction

p along the momentum p:

= c

p. (9.32)

9.3 London’s Equation: Penetration Depth 121

Thus if p = 0, there is a supercurrent density equal to

(2)

= (2e)(n

/2)c

p = en

. (9.33)

Similarly, −pairons contribute

(1)

=−en

= cp. (9.34)

Using the last three relations we repeat the calculations and obtain

=−⌳

pairon

A, ⌳

pairon

≡ 2e

−1

≡ ⌳, (9.35)

which we call a generalized London’s equation or simply London’s equation.This

differs from the original London equation (9.30) merely by a constant factor.

Let us now discuss a few physical consequences derivable from generalized Lon-

don’s equation (9.35). Taking the curl of this equation we obtain

∇×j

=−⌳∇×A =−⌳B. (9.36)

Using this and one of Maxwell’s equations

∇×H = j



⭸D

⭸t

= 0, j

= 0



(9.37)

(where we neglected the time-derivative of the dielectric displacement D and the

normal current j

), we obtain (Problem 9.3.3)

∇

B = B,λ≡ (c/e)

{

[

8πk

(

)

]

}

1/2

. (

≡ c

−2

) (9.38)

Here λ is called a generalized London penetration depth.

We consider the boundary of a semi-inﬁnite slab (superconductor). When an ex-

ternal magnetic ﬁeld B is applied parallel to the boundary, the B-ﬁeld computed

from Equation (9.38) can be shown to fall off exponentially (Problem 9.3.4):

B(x) = B(0) exp(−x/λ). (9.39)

(This solution is shown in Fig. 1.4.) Thus the interior of the superconductor, far from

the surface, will show the Meissner state: B = 0. Experimentally, the penetration

depth at lowest temperatures is on the order of 500

We emphasize that London’s equation (9.35) holds for the supercurrent j

only.

Since this is a strange equation, we shall rederive it by a standard calculation. The

effective Hamiltonian H for a +pairon moving with speed c

≡ v

(2)

/2is

H = c

. (9.40)

122 9 Supercurrents and Flux Quantization

In the presence of a magnetic ﬁeld B =∇×A, this Hamiltonian is modiﬁed to



= c

p −qA

. (9.41)

Assume now that the momentum B points in the x-direction. The velocity v

≡ ⭸H



/⭸p

= c

−1

−qA

). (9.42)

We calculate the quantum mechanical average of v

, multiply the result by the

charge 2e and the +pairon density, n

/2, and obtain

(2e)(n

/2)





= en



|

−2e

−1

. (9.43)

Adding the contribution of −pairons, we obtain the total current density j

= en

−c

)



|

−2e

−1

,. (9.44)

Comparing this with London’s equation (9.35) we see that the supercurrent arises

from the magnetic ﬁeld term for the pairon velocity v.

As another important application of Equation (9.22) let us consider a supercur-

rent ring. By choosing a closed path around the central line of the ring and integrat-

ing (⌬φ)

along the path ARA, we obtain from Equations (9.18) and (9.22)

(⌬φ)

motion

ARA

+2e

−1

ARA

A ·dr = kL = 2π n. (9.45)

The closed path integral can be evaluated by using Stoke’s theorem as

ARA

A ·dr =



dS ·∇×A =



dS ·B = BS ≡ ⌽, (9.46)

where S is the area enclosed by the path ARA, and ⌽ ≡ BS the magnetic ﬂux

enclosed. The phase difference due to the pairon motion (⌬)

motion

ARA

is zero since there

is no supercurrent along the central part of the ring. We obtain from Equations (9.45)

and (9.46)

⌽ = n⭸π e ≡ n⌽

, (9.47)

reconﬁrming the ﬂux quantization, see Equation (9.6).

Let us now choose a second closed path around the ring cavity but the one where

the supercurrent does not vanish. For example choose a path within a penetration

depth around the inner side of the ring. For a small section where the current runs

in the x-direction, the current due to a +pairon is

(2e)c





−4e

−1

, (9.48)

9.4 Quasi-Wavefunction and Its Evolution 123

where p

/p is the component of the unit vector

p pointing along the momentum p.

If we sum

p over the entire circular path, the net result is Equation (9.19)

ARA

p ·dr = 2πL. (9.49)

This example shows that the motional contribution to the supercurrent, part of

Equation (9.43): en





, does not vanish. Thus in this case the magnetic ﬂux

by itself is not quantized, but the lhs of Equation (9.45), called the ﬂuxoid, is quan-

tized.

Problem 9.3.1. Derive Equation (9.22).

Problem 9.3.2. Prove Stoke’s theorem Equation (9.27) for a small rectangle and

then for a general case.

Problem 9.3.3. Derive Equation (9.38).

Problem 9.3.4. Solve Equation (9.38) and obtain Equation (9.39).

9.4 Quasi-Wavefunction and Its Evolution

The quasi-wavefunction ⌽

(r) for a quasiparticle in the state ν is deﬁned by

⌽

(r) ≡ TR



†

φ(r)ρ



, (9.50)

⌿

(r) =



r|n|ν



. (9.51)

Here n is the pairon density operator; the corresponding density matrix elements

are represented by



μ|n|ν



≡ TR



†



. (9.52)

The density operator n, like the system-density operator ρ, can be expanded in

the form:

n =







, P

≥ 0, (9.53)

where





denote the relative probabilities that particle-states

{

}

are occupied.

It is customary in quantum many-body theory to adopt the following normalization

condition:







, (9.54)

124 9 Supercurrents and Flux Quantization

where

N is the total number operator. Using this, we obtain

tr{n}≡





ν|n|ν









ν|r



r|n|ν







, (9.55)

where

∗

(r) ≡



ν|r



[

(r) =



r|ν



]

(9.56)

is the wavefunction for a single pairon. If an observable X for the system is the sum

of single-particle observables ξ:

X =



( j)

, (9.57)

then the grand-ensemble average





can be calculated from





≡ TR

{

Xρ

}

= tr

{

ξn

}

, (9.58)

where the lhs means the many-particle average and the rhs the single-particle aver-

age. Using Equation (9.51) we can re-express tr

{

ξn

}

as:

{

ξn

}







ν|r



r|ξn|ν







r ψ

∗

(r)ξ(r, −i∇)⌿(r), (9.59)

where we assumed that ξ is a function of position r and momentum p: ξ = ξ(r, p).

Thus the average





for the many-particle system can be calculated in terms of the

quasi-wavefunction.

The system-density operator ρ(t) changes, following the quantum Liouville

equation:

i

⭸ρ

⭸t

= [H,ρ]. (9.60)

Using this, we study the time evolution of the quasi-wavefunction ⌿

(r, t).

First we consider the supercondensate at 0 K. The supercondensate at rest can be

constructed using the reduced Hamiltonian H





2

(1)

(1)†

(1)





2

(2)

(2)†

(2)

−











(1)†

(1)



(1)†

(2)†



(2)

(1)



(2)

(2)†



.(9.61)

Note: the electron kinetic energies are expressed in terms of the ground pairon

operators b



s. Let us recall that the supercondensate is generated from the physical

9.4 Quasi-Wavefunction and Its Evolution 125

vacuum by a succession of pair-creation, pair-annihilation and pair-transition via

phonon exchanges. In this condition, “electrons” (and “holes” ) involved are con-

ﬁned to a shell of energy-width ω

about the Fermi surface, and up- and down-spin

electrons are always paired (k ↑, −k ↓) to form ground pairons. This stationary

supercondensate cannot generate a supercurrent.

The moving supercondensate can be generated from the physical vacuum via

phonon exchanges. The relevant reduced Hamiltonian H

≡











( j)

(|k +q/2|) +

( j)

(|−k +q/2|)



( j)†

( j)

−











(1)†

(1)



(1)†

(2)†



(2)

(1)



(2)

(2)†



,(9.62)

which reduces to Equation (9.61) when q = 0. Supercondensation can occur at any

momentum q. The quasi-wavefunction ⌿

representing the moving superconden-

sate is

⌿

= A exp[i(q ·r −ω

t)], (9.63)

where the angular frequency ω

is given by

= qv

( j)

/2, (9.64)

a relation arising from the fact that pairons have energies



( j)

= w

+qv

( j)

/2. (9.65)

The Hamiltonian H

in Equation (9.62) is a sum of single-pairon energies. Hence

we can describe the system in terms of one-pairon density operator n. This operator

n(t) changes in time, following the one-body quantum Liouville equation:

i

⭸n

⭸t

= [h, n]. (9.66)

Let us now take a mixed representation of this equation. Introducing the quasi-

wavefunction for the moving supercondensate,



r|n|σ



≡ ⌿

(r), (9.67)

we obtain

i

⭸

⭸t

⌿

(r, t) = h(r, −i∇, t)⌿

(r, t), (9.68)

Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter - Superconductivity

Подождите немного. Документ загружается.