Franc J-P. Fundamentals of Cavitation

Подождите немного. Документ загружается.

7 - PARTIAL CAVITIES 153

The relation between noise and erosion has been studied since the fifties (see e.g.

ARGA & SEBESTYEN 1972). KATO, YE and MAEDA (1988) proved that cavitation noise

and pitting rate are strongly correlated on two-dimensional foils. This demonstrates

that both phenomena basically depend upon the rate of production of cavitating

structures. However, such a correlation cannot be used directly for the monitoring

of cavitation erosion in hydraulic machinery, since there is no major difference in

the noise signatures between erosive and non-erosive cavitation.

7.5. THERMAL EFFECTS IN PARTIAL CAVITATION

In the previous sections, heat transfer associated with phase change was disregarded.

In many practical situations and particularly in cold water, this simplification is

valid because the ratio of the vapor and liquid densities

is very small (about

1/60,000 for cold water). If so, the mass flowrate required to fill the cavity with

vapor is negligible and heat transfer associated with phase change is a secondary

phenomenon.

Referring to the case of a spherical bubble (see § 5.3.1), this assumption is valid far

from the critical point, which is the case of water at room temperature. When the

temperature increases and becomes close to the critical temperature, the ratio

increases and tends to unity. Heat transfer can no longer be ignored. This delays

the development of cavitation.

Due to thermal effects, the temperature inside the cavity is lower than in the liquid.

The vapor pressure is smaller and the cavitation parameter s

is greater, resulting

in reduced cavitation. This occurs, for example, in the case of cavitating inducers in

rocket engines using liquid hydrogen.

For partial cavitation, heat and mass transfer through the turbulent cavity interfaces

are complex phenomena. The situation is complicated by the re-entrant jet and its

unsteady character, and also by the possible two-phase nature of the cavity content

as mentioned in section 7.3.2. The problem is generally approached empirically, the

thermal effect usually taken as a correction to the mechanical problem which is

considered as the driving force in cavitation.

7.5.1. THE STEPANOFF B-FACTOR

The thermal delay in pumps was first investigated by STEPANOFF (1961).

mentioned in section 5.3.1, S

TEPANOFF defined the non-dimensional B-factor as the

inverse ratio of the volume of liquid

ᐂ

to be cooled to supply the heat necessary

for the production of a given volume

ᐂ

of vapor (see eq. 5.52):

1. See the reference in chapter 5.

FUNDAMENTALS OF CAVITATION154

== @

ᐂ

(7.10)

Here DT stands for the difference between the liquid bulk temperature T

•

and the

temperature T

inside the cavity, while Dp

is the corresponding variation in vapor

pressure. Evaluation of the B-factor allows us to estimate the pressure drop and the

increase.

A direct determination of the B-factor in liquid hydrogen and refrigerant 114 was

made by M

OORE and RUGGERI (1968) using similar Venturi nozzles with different

length scales (see tab. 7.1). All data were compared to a given reference case. The

authors proposed the following exponents for the effects of flow velocity, length

scale and cavity length on the B-factor:

ref

ref ref ref

08 02 03.. .

(/)

(7.11)

This correlation worked well for water, liquid nitrogen, liquid hydrogen and

refrigerant 114. As an example, the measured vapor pressure difference due to

thermal effects lies in the range 0.42 to 1.22 bars in liquid hydrogen at 20.3 K.

Liquid hydrogen Refrigerant 114

Length scale scale 0.7 scales 0.7 and 1

Throat diameter D (mm) 24.5 mm 24.5 and 35 mm

Temperature (K)

20 3 23 3..<<TK

255 303<<TK

Velocity (m/s)

33 5 62 5../<<Vms

615<<Vms/

Cavity length

10 26..<<l

D0226..<<l

Table 7.1 - Experimental conditions

The reference flow corresponds to the following conditions: refrigerant 114, scale 1,

ref

= 299

, V

ref

= 6.0 m/s,

l /.D

ref

= 072

ref

= 1.41 10

–4

/s,

ref

= 26.

[from MOORE & RUGGERI, 1968].

7.5.2. THE ENTRAINMENT METHOD

This method was derived by HOLL et al. (1975). The authors originally worked on

axisymmetric flows around ogives, but their model is also suitable to partial cavities

which develop on two-dimensional lifting foils or pump blades.

7 - PARTIAL CAVITIES 155

Principle

The flow is supposed steady. As vapor is released at the rear of the cavity, an

equivalent volumetric flowrate q

must be taken from the liquid and vaporized

through the cavity interface such that the cavity volume remains constant on

average (fig. 7.13). Because of heat transfer, a thermal boundary layer develops

along the cavity interface, through which the temperature falls from T

•

to T

. At

equilibrium, the cavity temperature T

is such that the vapor production flowrate

exactly balances the evacuated flowrate. The heat balance gives:

qL hT=Dl

(7.12)

where h is the mean heat transfer coefficient over the cavity of length l. Then:

(7.13)

This relation is made non-dimensional by introducing the following parameters:

— the N

USSELT number (based on the cavity length l):

— the R

EYNOLDS number (also based on l):

— the liquid P

RANDTL number:

Pr =

(a is the thermal diffusivity),

— the vapor flowrate coefficient:

∞

7.13 - Schematic illustration of vaporization in the front part of a cavity

and vapor entrainment by the outer liquid flow and re-condensation in the aft part

The temperature difference is then expressed by the following non-dimensional

equation:

Re Pr

(7.14)

FUNDAMENTALS OF CAVITATION156

The calculation of DT or of its non-dimensional form B requires evaluation of two

parameters:

— the flowrate coefficient C

, which characterizes the entrainment of vapor at the

rear of the cavity;

— the N

USSELT number Nu

, which characterizes heat transfer at the cavity interface.

Determination of the flowrate coefficient

Direct evaluation of the vapor flowrate coefficient is difficult. A rough estimate can

be obtained by using ventilation. An artificial cavity is formed in the original non-

cavitating flow by air injection. The procedure consists in adjusting the air flowrate

so that the ventilated cavity has the same apparent length as the vapor cavity. Of

course, those cavities are not quite similar since air is effectively incondensable. The

cavity ends are different, and because of air compressibility effects, the behavior of

the ventilated cavity depends to some extent upon the ambient pressure (see chap. 9).

Thus the method can only give an order of magnitude.

0 0.1 0.2 0.3

0.4

0.5

l/c

0.0052

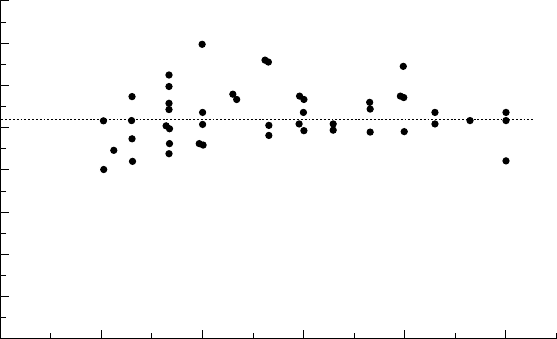
7.14 - Variation of the flowrate coefficient versus the reduced cavity length

for short cavities [from F

RUMAN et al., 1991]

RUMAN et al. (1991a) carried out such measurements for stable cavities (fig. 7.14),

i.e. for cavities whose length is smaller than half the foil chord length. Their results

are somewhat scattered but do not show any dependence on the cavity length. The

mean C

-value is 0.0052. KAMONO et al. (1993) confirmed this trend for short cavities

(

l /.c < 06

) and showed that the flowrate coefficient increases significantly with the

cavity length as the cavity begins to pulsate (

06 1./<<l c

The vapor flowrate q

can be expressed as

qeV

where e is the cavity thickness

and V

the mean velocity of the vapor inside the cavity. C

can be then written as:

7 - PARTIAL CAVITIES 157

(7.15)

For example, with

e/ %l = 5

and

= 0 0052.

, V

/V is equal to 0.1. The velocity of

the vapor inside the cavity is about an order of magnitude smaller than that of the

surrounding liquid.

Determination of the NUSSELT number

With respect to the NUSSELT number, the thermal boundary layer at the liquid-vapor

interface is hardly characterized. One possible way to approach heat transfer there

is to consider the interface as a solid wall and to estimate a value based on classical

convective heat transfer correlations.

One typical method of determination of the heat transfer coefficient is based upon

the R

EYNOLDS-COLBURN analogy between momentum and heat transfer. This gives

the following classical relation (see e.g. H

OLMAN 1997):

Nu C

RePr

(7.16)

where C

is the usual friction coefficient. Thus, the heat transfer is estimated on the

basis of the well-known friction coefficient.

Equation (7.14) becomes:

(7.17)

and the value of the friction coefficient C

is taken from empirical formulae.

If the interface is considered as a smooth flat plate in a turbulent flow, the following

correlation can be used:

0 074

(7.18)

It is often necessary to take into account the roughness of the liquid-vapor interface,

which significantly enhances heat transfer in comparison with the smooth case

RUMAN & BEUZELIN 1991b]. By introducing a roughness parameter e and assuming

that it is larger than the viscous boundary layer thickness, the mean friction

coefficient can be considered as independent of the R

EYNOLDS number and given

by the following correlation:

189 162

. . log

(7.19)

which is valid in the range

10 10

<<l /e

FUNDAMENTALS OF CAVITATION158

Application

As an example, the above procedure is applied to tests carried out by HORD (1972)

on partial cavities attached to foils, in liquid hydrogen and nitrogen. Temperature

measurements were made at five points inside the cavity. Table 7.2 presents a

comparison between calculated and measured data.

Liquid

hydrogen

Liquid

nitrogen

Liquid temperature

T (K)

•

20.70 77.71

Cavity length

l (mm)

44.4 50.8

Flow velocity

V(m/s)

59.4 23.9

RANDTL number 1.28 2.29

EYNOLDS number

1.45 10

6.49 10

Friction coefficient C

smooth wall

e=005.mm

e=05.mm

0.0027

0.0087

0.0175

0.0032

0.0084

0.0167

Vapor flowrate coefficient C

0.0052

␳␳

L / c (K)

0.95 0.57

Calculated B-factor

smooth wall

e=005.mm

e=05.mm

4.53

1.41

0.69

5.63

2.14

1.09

Calculated

⌬T (K)

smooth wall

e=005.mm

e=05.mm

4.30

1.34

0.66

3.21

1.22

0.62

Measured

⌬T (K)

is the distance, from the leading edge,

of the station where cavity temperature

was measured)

xmm

11=

xmm

17 3= .

xmm

26 8= .

xmm

36 5= .

1.8

2.0

2.3

2.4

1.9

2.3

2.2

2.0

Table 7.2

In the absence of values for the flowrate coefficient C

, use is made of the above-

mentioned value 0.0052.Three different assumptions are considered for the estimation

of the friction coefficient C

— the smooth wall,

— wall roughness

e=005.mm

— wall roughness

e=05.mm

The friction coefficient increases with roughness, so that the temperature shift

decreases. As seen from the table, the experimental values are within the range

covered by the three assumptions.

7 - PARTIAL CAVITIES 159

In the above approach, the cavity is supposed filled with vapor with heat transfer

occurring through the cavity interface. In fact, the void fraction inside the cavity

may be smaller than unity [S

TUTZ et al. 1998] and the cavity may contain droplets

whose area should contribute to the total interfacial area. If so, this model is no

longer entirely appropriate. However, in the framework of the present approach,

the effect of any increase in the interfacial area can be taken into account empirically

by adjustment of the roughness e which remains a free parameter of the model

RUMAN & BEUZELIN 1991b].

7.6. SYSTEM INSTABILITY

In section 7.3, the cloud cavitation instability was discussed. This instability is

intrinsic, in so far as it results from the dynamics of the cavity proper. Unlike the

case of cloud cavitation, other instabilities which result from a coupling of the

cavity dynamics with the rest of the hydraulic circuit can develop. Cavitation surge

is a typical example of such a system instability.

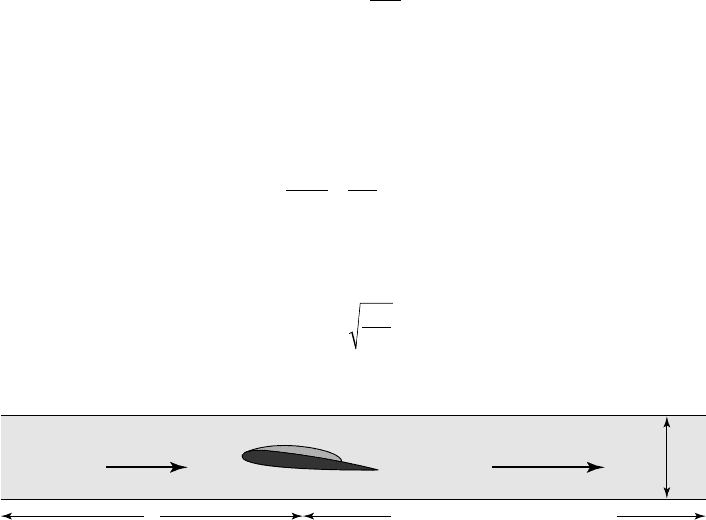
To illustrate it, consider a cavitating hydrofoil in a duct of area A (fig. 7.15). A

simplified one-dimensional model is used to analyse this configuration [W

ATANABE

et al. 1998]. For simplicity, the downstream length is supposed infinite, so that the

mass flowrate m [kg/s] downstream remains constant due to infinite inertia.

In steady state conditions, the cavity volume ᐂ, the mass flowrate m and the

pressure p in any cross-section are constant if head losses are neglected.

Under unsteady conditions, the fluctuation of mass flowrate in the upstream line is

denoted m'(t) with p'(t) as the pressure fluctuation at the location of the hydrofoil.

The inlet pressure is supposed constant. The momentum balance in the upstream

duct is written:

(7.20)

As for the mass balance, it simply states that the variations in cavity volume are

balanced by the fluctuations in the incoming flowrate:

'=-r

ᐂ

(7.21)

Introduction of the classical cavitation compliance K allows us to state that variations

in cavity volume are linearly related to the variations in pressure:

ᐂ

(7.22)

FUNDAMENTALS OF CAVITATION160

In other words, the cavitation compliance expresses how the cavity volume changes

with the local pressure:

=-r

ᐂ

(7.23)

Cavitation compliance results from purely quasi-static considerations and do not

involve any dynamic feature of the cavity.

By combining equations (7.20), (7.21) and (7.22), we get the following equation for

the pressure fluctuation:

'+=

(7.24)

The type of solution depends upon the sign of the cavitation compliance K. If K is

positive, all the variables exhibit periodic oscillations at the frequency:

(7.25)

which is the natural frequency of the system made up of the cavity and the inlet line.

Infinite downstream len

p = Constant

Cavity volume

p + p'

m + m'

m = Constant

7.15 - The case of an isolated cavitating foil in a duct

For simplicity, the downstream length is supposed infinite.

This regime is typical of cavitation surge. The physical reason for oscillations is easy

to understand. If it is supposed that the pressure at the location of the hydrofoil

decreases, the cavity volume increases because of a positive value of the cavitation

compliance. By continuity, the incoming flowrate decreases and the inertia of the

upstream column makes the pressure at the location of the hydrofoil increase. Hence,

the situation is stable and auto-oscillations develop.

From equation (7.25), it appears that the frequency of the pulsations results from

a coupling between the cavity, characterized by its compliance, and the inlet line,

characterized by its length L and area A. This behavior is typical of a system

instability.

If the cavitation compliance were negative, the solution would not be periodic but

would increase exponentially and the behavior would be unstable. In fact, the length

of a cavity and hence its volume normally increases when the pressure decreases

(see fig. 7.3), so that the cavitation compliance is usually positive. Hence, such an

unstable behavior connected to negative values of the cavitation compliance is rather

unusual.

7 - PARTIAL CAVITIES 161

The above covers the basic case of cavitation surge for an isolated hydrofoil in a

duct. The principle of the analysis remains applicable to more complicated cases.

UTTWEILER and BRENNEN (2002) examined surge instability on a cavitating propeller

tested in a water tunnel using the theoretical approach developed by B

RENNEN and

COSTA (1973). The procedure the authors developed illustrates the main steps to

follow, in order to analyse a cavitation surge instability. The cavitation dynamics

and the facility dynamics are considered as part of a coupled system. Each of them

has to be characterized in order to predict the whole system dynamics. The main

steps of the prediction are:

® The quasi-steady state response of the cavitation volume to changes in inlet

conditions is characterized in terms of a cavitation compliance K and a mass

flow gain factor M. The cavitation compliance describes the variation in cavity

volume with pressure (see eq. 7.23), whereas the mass flow gain factor describes

the variation in cavity volume with the angle of attack. The mass flow gain factor

is needed for the modeling of cavitation instabilities in turbomachinery, because

a change in inlet flowrate results in a change in angle of attack, as can be seen

from consideration of the velocity triangle.

® The second step consists in modeling the dynamics of the facility by dividing it

into

elementary components (pipes, tanks…) of specified "resistance", "capacitance"

and "inertance".

® Finally, the facility dynamics and the cavitation dynamics have to be coupled in

order to identify potentially unstable behavior.

By applying the previous procedure to the case of a propeller in a cavitation tunnel,

UTTWEILER (2001) succeeded in predicting the characteristic frequency of the

observed instability. This procedure can be followed for the analysis of any partial

cavity instability of surge type.

7.7. PARTIAL CAVITY FLOW MODELING

The modeling of partial cavities is very similar to the case of supercavities, concerning

the conditions for detachment from the solid wall and the boundary condition at

the interface. However, the cavity termination and the reattachment of the flow to

the wall bring additional difficulties, as well as the unsteady behavior of the cavity.

Ad hoc methods (and even artifices) were used to reach agreement with the

experimental results and particularly for the dependence of the cavity length or the

drag and lift coefficients on the cavitation parameter. An abundant literature has

been devoted to this topic since the mid-seventies.

As for the steady state, both closed and open models have been developed. For

closed models, the closure condition can be imposed right at the cavity termination

or along a transition zone, whose length is adjusted for best representation of the

flow. The reattachment of the flow to the wall gives a curvature to the interface

FUNDAMENTALS OF CAVITATION162

which is directed towards the liquid and generates an overpressure near the cavity

closure. Generally, such closed models do not result in a one-to-one relation l(s)

(see e.g. N

ISHIYAMA & ITO 1977, LEMONNIER & ROWE 1988). They are more

appropriate to the modeling of short and thin cavities, which only weakly disturb

the flow.

Thick cavities, however, are best represented by open models in which the cavity

is followed by a wake whose displacement thickness is constant or increases

downstream. Such a wake can be generated by sources blowing at the cavity end

or through a permeable wall [Y

AMAGUCHI & KATO 1983, ITO 1986, ROWE &

LOTTIAUX 1993]. It induces an additional drag which simulates the dissipation

associated with thick cavities.

As for unsteady cavities, a detailed presentation of the main difficulties in the

modeling of partial cavity flows based on the classical non-linear inviscid theory

(with the effects of viscosity on cavity detachment and cavity wake included) can

be found in K

INNAS (1998), together with a comprehensive review of the main

works devoted to 2D and 3D cavity flow modeling.

Other approaches have been developed to model unsteady cavitation on the basis

of either the E

ULER or NAVIER-STOKES equations completed with a cavitation model.

A homogeneous fluid of variable density is usually considered to represent the

water-vapor mixture. As an example, the barotropic model [Reboud & Delannoy

1994] introduces a constitutive law r(p) for this equivalent fluid whose density is

assumed to change continuously from the vapor density to the liquid density when

the pressure curve crosses the vapor pressure value. There is also the two-phase

bubble flow model [K

UBOTA et al. 1992] wherein the cavity is considered as a

homogeneous cluster of spherical bubbles. The local void fraction is computed from

the resolution of a R

AYLEIGH-PLESSET equation for the bubble cluster. Such a model,

which requires the stipulation of a nuclei density, satisfactorily simulated the cyclic

behavior of partial cavities.

REFERENCES

BRENNEN C.E. & ACOSTA A.J. –1973– Theoretical quasi-static analyses of cavitation

compliance in turbopumps. J. Spacecraft and Rockets 10(3), 175-180.

ALLENAERE M. –1999– Étude physique des poches de cavitation partielle

en écoulement interne. Thesis, Grenoble University (France).

ALLENAERE M., FRANC J.P. & MICHEL J.M. –2001– The cavitation instability

induced by the development of a re-entrant jet. J. Fluid Mech. 444, 223-256.

E M.K. & HAMMITT F.G. –1982– New method for monitoring and correlating

cavitation noise to erosion capability. J. Fluids Eng. 104, 434-442.

E LANGE D.F. –1996– Observation and modelling of cloud formation behind

a sheet cavity. PhD Thesis, Twente University (the Netherlands).