Fishwick P.A. (editor) Handbook of Dynamic System Modeling
Подождите немного. Документ загружается.

36-8 Handbook of Dynamic System Modeling
The first two lines state that pressure p and specific enthalpy h in the connection point are identical. Since
all other intensive quantities of a multiphase fluid (e.g., density, or specific entropy) can be computed from
p and h, the medium state is uniquely defined. The third and fourth equations state the mass and energy
balance for an infinitesimal small control volume in the connection point. Together with the remaining
equations for port.H_flow in the components, a linear system of equations is present to compute the
mixing enthalpy A.port.h =B.port.h =C.port.h in the connection point. It has the solution:
A.port.h = -( (if A.port.m_flow > 0 then 0 else A.port.m_flow*A.h)+
(if B.port.m_flow > 0 then 0 else B.port.m_flow*B.h)+
(if C.port.m_flow > 0 then 0 else C.port.m_flow*C.h) )
/( (if A.port.m_flow > 0 then A.port.m_flow else 0)+
(if B.port.m_flow > 0 then B.port.m_flow else 0)+
(if C.port.m_flow > 0 then C.port.m_flow else 0) )
Therefore, independently of the flow directions in the three ports, the mixing enthalpy is always uniquely
computed, provided at least one mass flow rate does not vanish (see Elmqvist et al., 2003 for details how
to handle the case if all mass flow rates vanish). From the mixing enthalpy and the port pressure, all other
mixing quantities can be computed, such as mixing temperature.
In the Modelica standard library (see below), elementary connectors for all important technical domains
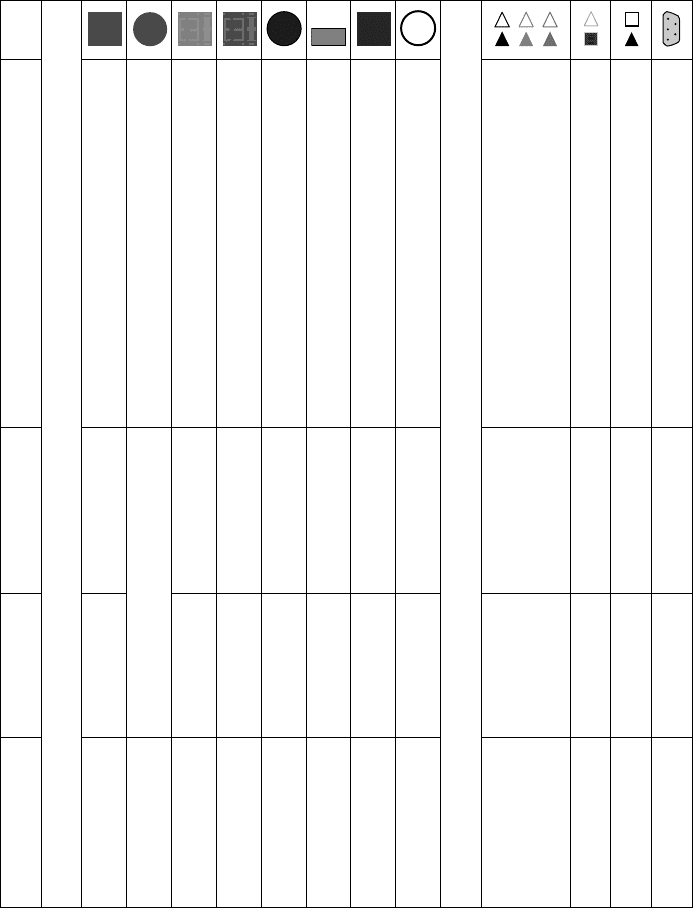
are provided. The definition of these connectors is summarized in the Table 36.1.
Column “type” is the physical domain, column “potential” defines the variables in the connector that
have no “flow” prefix, column “flow” defines the variables with a “flow” prefix, column “connector name”
defines the connector class name where the definition is present and column “icon” is a screenshot of the
connector icon.
For three-dimensional mechanical systems, the position vector r[3] from the origin of the world frame to
the origin of the connector frame, the transformation matrix T[3,3] from the world to the connector frame,
as well as the cut-force vector f[3] and the cut-torque vector t[3] are utilized. The transformation matrix
T[3,3] contains a redundant set of variables. In Otter et al. (2003) it is described how the information about
the constraint equations of T is defined in Modelica, and how a tool can automatically remove connection
restrictions due to this redundancy based on this additional information. In Modelica, array dimensions
are declared with square brackets, e.g., A[3,4] is a two-dimensional array where the first dimension has
size 3 and the second size 4. A dimension size specified as “:”, e.g., Xi[:], defines an unknown dimension
that can be defined when using the array.
Type “thermal” refers to heat transfer. Note, in bond graph methodology temperature and entropy flow
rate are used as connector variables, because the product of these two variables is the energy flow through
the port. The definition in the Modelica Standard Library with temperature and heat flow rate also fulfills
the energy balance in a connection point. It has the additional advantage that lumped elements, such as a
thermal conductor, a thermal capacitor or the “fully isolated boundary condition” lead to linear equations
in the connector variables, whereas the bond graph approach leads to nonlinear equations.
Type “thermo-fluid pipe flow” refers to one-dimensional thermo-fluid flow in pipe networks with
incompressible or compressible media that may have one or multiple (homogenous) phases and/or one
or multiple substances. The potential variables in the connector are pressure p, specific mixing enthalpy h,
and the vector of independent mixture mass fractions Xi[:]. The flow variables are mass flow rate
m
flow
, enthalpy flow rate H
flow
and the vector of the independent substance mass flow rates mXi
flow
[:].
When only one substance is present, vectors Xi and mXi
flow
have dimensions zero and are therefore not
present. More detailed information of this connector is available in Elmqvist et al. (2003) and in the
Modelica.Fluid.UsersGuide.
Besides physical connectors, also a set of signal connectors are provided, especially for block diagrams
and for hierarchical state machines. Type “signal bus” characterizes an empty connector that has the
additional prefix “expandable.” This connector type is used to define a hierarchical collection of named
signals where the full connector definition (containing all signal definitions) is defined implicitly by the
Multidomain Modeling with Modelica 36-9
TABLE 36.1
Connector Definitions in the Modelica Standard Library
Type
Potential
Flow Variables
Connector Name (Modelica Library)
Icon
Physical connectors
Electric analog
Electric potential
Electric current
Modelica.Electrical.Analog.Interfaces.Pin
Electric multi-phase
Vector of electrical pins
Modelica.Electrical.MultiPhase.Interfaces.Plug
Magnetic
Magnetic potential
Magnetic flux
Modelica.Magnetic.Interfaces.MagneticPort
Translational
Distance
Force
Modelica.Mechanics.Translational.Interfaces.Flange
Rotational
Angle
To r q u e
Modelica.Mechanics.Rotational.Interfaces.Flange
3D mechanics
r[3], T[3,3]
f[3], t[3]
Modelica.Mechanics.MultiBody.Interfaces.Frame
Thermal
Temperature
Heat flow rate
Modelica.Thermal.HeatTransfer.Interfaces.HeatPort
Thermo-fluid pipe flow
p, h, Xi[:]
m
flow
, H
flow
, mXi
flow
[:]
Modelica.Fluid.Interfaces.FluidPort
Signal connectors
Signal
Real
None
Modelica.Blocks.Interfaces.RealInput/Output
Integer
Modelica.Blocks.Interfaces.IntegerInput/Output
Boolean
Modelica.Blocks.Interfaces.BooleanInput/Output
Electric digital
Integer (1
...9)
None
Modelica.Electrical.Digital.Interfaces.DigitalSignal
State machine
Booleans
None
Modelica.StateGraph.Interfaces.Step_in/Transition_in
Signal bus
Configurable
None
Modelica.Blocks.Interfaces.SignalBus
36-10 Handbook of Dynamic System Modeling
set of variables occurring in all connections of this type. This connector is used to communicate a large
amount of signals in a convenient way between components.
Modelica supports also hierarchical connectors, in a similar way as hierarchical models. As a result, it is,
e.g., possible, to collect elementary connectors together. For example, an electrical plug consisting of two
electrical pins can be defined as:
connector Plug
Pin phase;
Pin ground;
end Plug;
With one connect(..) equation, either two plugs can be connected (and therefore implicitly also the phase
and ground pins) or a Pin connector can be directly connected to the phase or ground of a Plug connector,
such as “connect(resistor.p, plug.phase).” A predefined connector of this type is the “electrical multiphase”
connector (see table above), that contains a vector of pins, with a default dimension of 3, i.e., it allows a
convenient description of multiphase networks.
Besides “one-to-one” connections of components on the same hierarchical level, also “one-to-many”
connections over component hierarchies can be conveniently defined with the inner/outer language
construct to model the coupling of components with physical fields. Typical examples are bodies in the
gravity field of the earth where the gravity acceleration depends on the body position. A language construct
to model conveniently connections where every object is connected to any other object of a general physical
fields is currently under development.
36.2.2 Discontinuous Systems
After the presentation of the fundamental structuring mechanisms in Modelica and the means to describe
continuous models, attention is now given to discrete modeling features, especially the difficult problem
how to synchronize continuous and discrete components: In Modelica, the central property is the usage
of synchronous differential, algebraic, and discrete equations. Synchronous languages (Halbwachs, 1993;
Benveniste et al., 2003), such as SattLine (Elmqvist, 1992), Lustre (Halbwachs et al., 1991), or Signal (Gau-
tier et al., 1994) have been used to model discrete controllers to yield safe implementations for real-time
systems and to verify important properties of the discrete controller before executing it. The idea of gener-
alizing the data flow principle of synchronous languages in the context of continuous/discrete systems was
introduced in Elmqvist et al. (1993) and further improved in Otter et al. (1999) and Elmqvist et al. (2001).
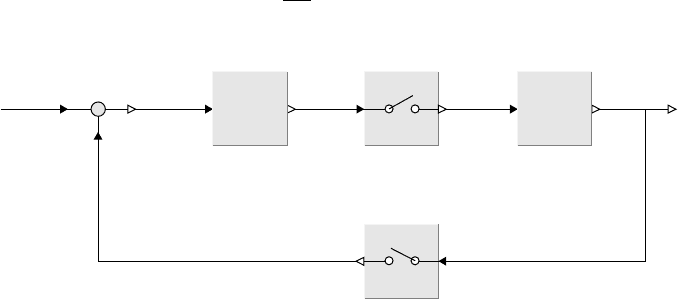
A typical example of a (continuous/discrete) hybrid model is given in Figure 36.4
where a continuous plant
dx
p
dt
= f (x
p
, u)
y = g(x
p
)
PlantController
r
uy
FIGURE 36.4 Continuous plant controlled by a discrete controller.
Multidomain Modeling with Modelica 36-11
is controlled by a digital linear controller
x
c
(t
i
) = Ax
c
(t
i
−T
s
) +B(r(t
i
) −y(t
i
))
u(t
i
) = Cx
c
(t
i
−T
s
) +D(r(t
i
) −y(t
i
))
using a zero-order hold to hold the control variable u between sample instants (i.e., u(t) =u(t
i
) for
t
i
≤t < t
i
+T
s
), where T
s
is the sample interval, x
p
(t) is the state vector of the continuous plant, y(t)
is the vector of measurement signals, x
c
(t
i
) is the state vector of the digital controller and r(t
i
)isthe
reference input. In Modelica, the complete system can be easily described by connecting appropriate
blocks. However, for simplicity of the discussion, here an overall description of the system is given in one
model where the discrete equations of the controller are within the when clause below.
model SampledSystem
parameter Real Ts=0.1 "sample period";
parameter Real A[:, size(A,1)], B[size(A,1), :],
C[:, size(A,2)], D[size(C,1),size(B,2)];
input Real r[size(B,2)] "reference";
output Real y[size(B,2)] "measurement";
Real u [size(C, 1)] "actuator";
Real xc[size(A, 1)] "controller state";
Real xp[:] "plant state";
equation
der(xp) = f(xp, u); // plant
y = g(xp);
when sample(0,Ts) then // digital controller
xc=A*pre(xc) + B*(r-y);
u=C*pre(xc) + D*(r-y);
end when;
end SampledSystem;
During continuous integration the equations within the when clause are deactivated. When the condition
of the when clause becomes true, an event is triggered, the integration is halted and the equations within
the when clause are active at this event instant. The operator sample(. ..) triggers events at sample
instants with sample time T
s
and returns true at these event instants. At other time instants it returns
false. The values of variables are kept until they are explicitly changed. For example, u is computed only
at sample instants. Still, u is available at all time instants and consists of the value calculated at the last
event instant. The equations in a when clause are called “discrete equations” since they are only active at
distinct points in time. Equations in a when clause have the restriction that on one side of the “=” sign
only a variable reference and no expression is allowed to identify uniquely the variable of the equation that
“holds” its value when the equation is not active.
At a sampling instant t
i
, the controller needs the values of the controller state x
c
for the time t
i
and for
the previous sample instant t
i
−T
s
, which is determined by using the pre operator. Formally, the left limit
x(t
−
) of a variable x at a time instant t is characterized by pre(x), whereas x itself characterizes the right
limit x(t
+
). Since x
c
is only discontinuous at sample instants, the left limit x
c
(t
−
i
) at sample instant t
i
is
identical to the right limit x
c
(t
+
i
−T
s
) at the previous sample instant and therefore pre(xc) characterizes
this value.
The generalized synchronous principle introduced in Elmqvist et al. (1993) states that at every time
instant the active equations express relations between variables that have to be fulfilled concurrently at the
current time instant. As a consequence, during continuous integration the equations of the plant have
to be fulfilled, whereas at sample instants the equations of the plant and of the digital controller hold
concurrently. To efficiently solve such types of models, all equations are sorted under the assumption that

36-12 Handbook of Dynamic System Modeling
all equations are active (details see below). In other words, the order of the equations is determined by
data flow analysis resulting in an automatic synchronization of continuous and discrete equations. For the
example above, sorting results in an ordered set of assignment statements:
// "input" variables provided from environment: r, xp, pre(xc)
y := g(xp);
when sample(0,Ts) then
xc := A*pre(xc) + B*(r-y);
u:=C*pre(xc) + D*(r-y);
end when;
der(xp) := f(xp, u);
Note, that the evaluation order of the equations is correct (in the sense that all active equations are
concurrently fulfilled) both when the controller equations are active (at sample instants) and when they
are not active.
The (generalized) synchronous principlehasseveral consequences. First, evaluation of discrete equations
is performed in zero (simulated) time, i.e., Modelica has instantaneous communication (Benveniste et al.,
2003). If needed, it is possible to model the computing time by explicitly delaying the assignment of
variables. Second, unknown variables are uniquely computed from a system of equations,
5
i.e., Modelica
has deterministic concurrency (Benveniste et al., 2003). This implies that the number of active equations
and the number of unknown variables in the active equations at every time instant are identical. This
requirement is, for example, violated in
equation // incorrect model fragment!
when h1> 3 then
close = true;
end when;
when h2<1then
close = false;
end when;
If by accident or on purpose the relations h1 > 3 and h2 < 1becometrue at the same time instant, we have
two conflicting equations for close and it is not defined which equation should be used. In general, it is
not possible to detect by source inspection whether conditions become true at the same event instant or
not. Therefore, in Modelica the assumption is used that all equations in a model may potentially be active at
the same time instant during simulation. Owing to this assumption, the total number of (continuous and
discrete) equations shall be identical to the number of unknown variables. It is often possible to rewrite
the model above by placing the when clauses in an algorithm section and changing the equations into
assignments
algorithm algorithm
when h1>3then when h2<1then
close := true; close := false;
end when; or alternatively elsewhen h1>3then
when h2<1then close := true;
close := false; end when;
end when;
5
Nonlinear equations may have multiple solutions. However, starting from user defined initial conditions, the
desired solution is uniquely identified.

Multidomain Modeling with Modelica 36-13
Filltank1
Level1
> limit Level1 < 0.001True
00
Waittime Waittime
True
Filltank2 Emptytank2T1 T4T3Wait1 Wait2T2
FIGURE 36.5 Part of a Modelica StateGraph to fill and empty a tank system.
The algorithm section groups the two when clauses so that they are evaluated sequentially in the order of
appearance and the second one get higherpriority. All assignment statements within the same algorithm
section are treated as a set of n equations, where n is the number of different left-hand side variables (e.g.,
the model fragment above corresponds to one equation in the unknown “close”). An algorithm section
is sorted as one entity together with the rest of the system. Another assignment to close somewhere else
in the model would still yield an error.
Handling hybrid systems in this way has the advantage that the synchronization between the continuous
time and discrete event parts is automatic and leads to a deterministic behavior. Problems are detected
during translation, e.g., nondeterministic concurrency (a variable is defined by two or more equations) or
deadlock (an algebraic loop between different when clauses).
The Modelica language elements for discrete systems are especially used to implement library
components on a higher level to define discrete systems in a convenient way graphically, such as
•
discrete input/output blocks (Modelica.Blocks.Discrete, Modelica.LinearSystems.Sampled),
•
logical blocks (Modelica.Blocks.Logical), and
•
hierarchical state machines (Modelica.StateGraph) (Otter et al., 2005).
The Modelica.StateGraph library is based on a subset of JGraphcharts (Årzen et al., 2002) that is an
enhanced version of the industrial standard Grafcet/Sequential Function Charts (IEC 848 and IEC
61131-3). JGraphcharts and StateGraphs have a similar modeling power as Statecharts. A simple example
is shown in Figure 36.5 containing part of the definition to fill and empty a tank system. For example, if the
state machine is in step “fillTank1” and the Boolean condition “level1 > limit” of transition T1 becomes
true, then the state machine switches to step “wait1.” The basic ideas to implement state machines in
Modelica with Boolean equations are described in Mosterman et al. (1998) and Elmqvist et al. (2001).
In Grafchart, Grafcet, Sequential Function Charts, and Statecharts, actions are usually formulated within
a step or a state. Such actions are distinguished as entry, normal, exit, and abort actions. For example,
a valve might be opened by an entry action of a step and might be closed by an exit action of the same
step. In StateGraphs this is not possible due to the (generalized) synchronous principle explained above,
which does not allow that one variable is defined by two equations. Instead, Boolean equations are added
to a StateGraph to set the valve according to the StateGraph state, e.g.,
valve2 = fillTank2.active or emptyTanks.active and level1 > limit
This feature of a StateGraph is very useful, since it allows a Modelica translator to guarantee that a given
StateGraph has deterministic behavior without conflicts. For example, if the valve is opened and closed in
different steps, the Boolean equation for the valve defines uniquely the priority if several steps influencing
the valve would be active at the same time instant, e.g., by parallel execution branches.
36.2.3 Relation-Triggered Events
During continuous integration it is advantageous that the model equations remain continuous and differ-
entiable, since the numerical integration methods are based on this assumption. This requirement is often
36-14 Handbook of Dynamic System Modeling
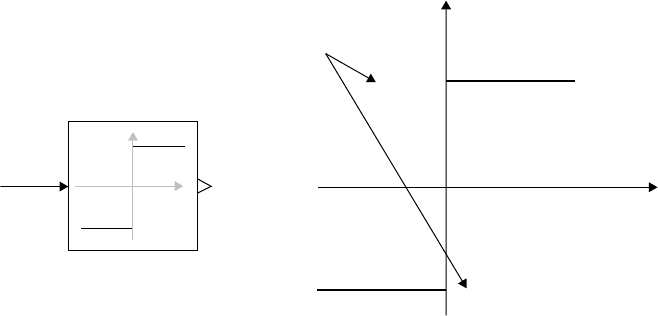
During event iteration
Twopoint
u
u
y
y
y0 1
FIGURE 36.6 Two point switch block to demonstrate relation-triggered events.
violated by if-clauses. For example the two-point switch block in Figure 36.6 with input u and output y
may be described by
model TwoPoint
parameter Real y0=1;
input Real u;
output Real y;
equation
y=if u>0then y0 else -y0;
end TwoPoint;
At point u=0 this equation is discontinuous, if the if-expression would be taken literally. A discontinuity
or a nondifferentiable point can occur if a relation, such as x
1
> x
2
changes its value, because the branch of
an if-statement may be changed. Such a situation can be handled in a numerical sound way by detecting
the switching point within a prescribed accuracy, halting the integration, selecting the corresponding new
branch, and restarting the integration, i.e., by triggering a state event.
In general, it is not possible to determine by source inspection whether a specific relation will lead to
a discontinuity or not. Therefore, in Modelica it is by default assumed that every relation will potentially
introduce a discontinuity or a nondifferentiable point in the model. Consequently, relations automatically
trigger state events (or time events for relations depending only on time) at the time instants where their
value is changed. This means, e.g., that model TwoPoint is treated in a numerical sound way: during the
iteration to determine the time instant when u crosses zero, the if-expression remains on the branch that it
had before the iteration started, i.e., during zero crossing detection the relation u > 0 is not taken literally.
Modelica has several operators for hybrid systems, such as smooth(...), noEvent(...) to switch off
event handling and treat relations literally, reinit(x, value) to reinitialize a continuous state with
a new value at an event instant, initial() to inquire the first and terminal() to inquire the last
evaluation of the model during a simulation run.
36.2.4 Variable Structure Systems
If a physical component is modeled (macroscopically) precisely enough, there are no discontinuities in
a system. When neglecting some “fast” dynamics, to reduce simulation time and identification effort,
Multidomain Modeling with Modelica 36-15
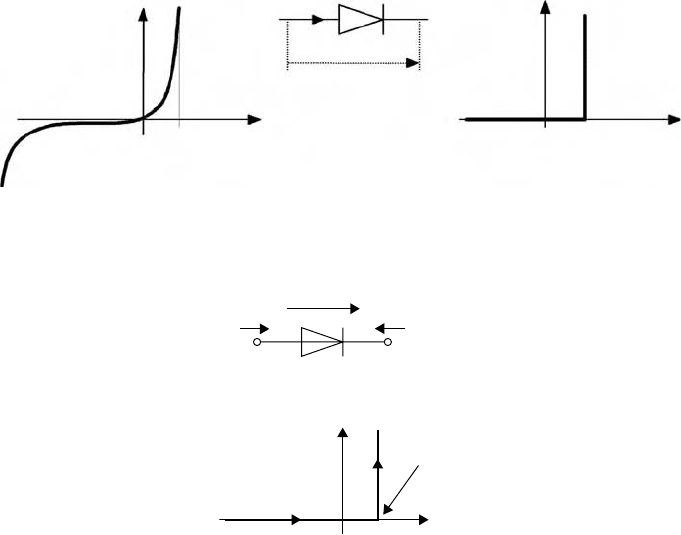
Detailed diode
model
Idealized diode
model
i
i
i
u
u
u
knee
u
knee u
FIGURE 36.7 Detailed and idealized diode characteristic.
u
u
knee
u
i
2
i
1
i
1
v
2
S
S
S 0
v
1
FIGURE 36.8 Declarative description of an ideal diode model.
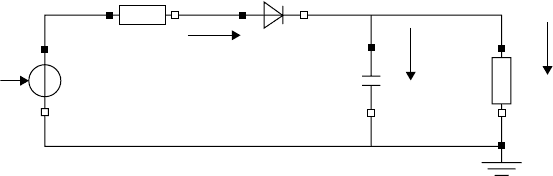
discontinuities may appear. As a typical example, consider modeling of a diode, where i is the current
through the diode and u is the voltage drop between its pins.
The diode characteristic is shown in the left part of Figure 36.7. If the detailed switching behavior can
be neglected with regard to other modeling effects and the diode shall be used in its “operating range,”
it is advantageous to use the ideal diode curve shown in the right part of Figure 36.7. It typically gives a
simulation speedup of 1–2 orders of magnitude.
It is straightforward to model the detailed diode curve, because the current i has just to be given as
(analytic or tabulated) function of the voltage drop u. It is more difficult to model the ideal diode curve
in the right part of Figure 36.8, because the current i at u =u
knee
is no longer a function of u, i.e.,
a mathematical description in the form i =i(u) is no longer possible. This problem can be solved by
introducing a curve parameter s and describing the curve as i =i(s) and u =u(s). This description form is
more general and allows defining an ideal diode uniquely in a declarative way:
equation
0=i1+i2;
u=v1-v2;
on=s>0;
u = uknee + (if on then 0 else s);
i1 = if on then s else 0;
To understand the consequences of parameterized curve descriptions, the ideal diode is used in the simple
rectifier circuit of Figure 36.9.
36-16 Handbook of Dynamic System Modeling
Resistor2
R R
2
R R1
i1
i2
Ground
C C
Voltagesource
i0
v0
Resistor1
Idealdiode
v1 v2
Capacitor
FIGURE 36.9 Simple electrical circuit to demonstrate the handling of an ideal diode model.
Collecting the equations of all components and connections, as well as sorting and simplifying the set of
equations under the assumption that the input voltage v
0
(t) of the voltage source is a known time function
and that the states (here: v
2
) are assumed to be known and the derivatives should be computed, leads to
on=s>0;
u=v1-v2;
u = uKnee + (if on then 0 else s);
i0 = if on then s else 0;
R1*i0 = v0 - v1;
i2:= v2/R2;
i1:= i0-i2;
der(v2):= i1/C;
The first five equations build a system of equations in the five unknowns on, s, u, v1, and i0.The
remaining assignment statements are used to compute the state derivative der(v2). During continuous
integration the Boolean variables, i.e., on, are fixed and the Boolean equations are not evaluated. In this
situation, the first equation is not touched and the next four equations form a linear system of equations
in the four unknown variables s, u, v1, and i0, which can be solved by Gaussian elimination. An
event occurs if one of the relations (here: s>0) changes its value.
At an event instant, the first five equations are a mixed system of discrete and continuous equations that
cannot be solved by, say, Gaussian elimination, since there are both Real and Boolean unknowns. However,
appropriate algorithms can be constructed: (1) Make an assumption about the values of the relations in
the system of equations. (2) Compute the discrete variables. (3) Compute the continuous variables by
Gaussian elimination (discrete variables are fixed). (4) Compute the relations based on the solution of (2)
and (3). If the relation values agree with the assumptions in (1), the iteration is finished and the mixed
set of equations is solved. Otherwise, new assumptions on the relations are necessary, and the iteration
continues. Useful assumptions on relation values are for example: (a) Use the relation values computed in
the last iteration and perform a fixed-point iteration (the convergencecan be enhanced by some algorithmic
improvements). (b) Try all possible combinations of the values of the relations systematically (exhaustive
search). In the above example, both approaches can be simply applied, because there are only two possible
values (s > 0 is false or true). However, if n switches are coupled, there are n relations and therefore 2
n
possible combinations which have to be checked in the worst case.
The technique of parameterized curve descriptions was introduced in (Claus et al., 1995) and a series of
related papers. However, no proposal was given on how to implement such models in a numerically sound
way. In Modelica, the solution method follows logically because the equation-based system naturally leads
to a system of mixed continuous/discrete equations, which have to be solved at event instants (Otter et al.,
1999).

Multidomain Modeling with Modelica 36-17
Alternative approaches to treat ideal switching elements are (a) by using variable structure equa-
tions that are controlled by state machines to describe the switching behavior (see, e.g., Barton, 1992;
Elmqvist et al., 1993; Mosterman and Biswas, 1996), or by (b) using a complementarity formulation (see,
e.g., Lötstedt, 1982; Pfeiffer and Glocker, 1996; Schumacher and van der Schaft, 1998). The approach (a)
has the disadvantage that the continuous part is described in a declarative way but not the part describing
the switching behavior. As a result, algorithms with better convergence properties for the determination of
consistent switching structure cannot be used. Furthermore, this involves a global iteration over all model
equations whereas parameterized curve descriptions lead to local iterations over the equations of the
involved elements. The approach (b) seems to be difficult to use in an object-oriented modeling language
and seems to be applicable only in special cases (e.g., it does not seem possible to describe ideal thyristors).
Note, mixed systems of equations do not only occur if parameterized curve descriptions are used, but
also in other cases, e.g., whenever an if-statement is part of an algebraic loop and the expression of the
if-statement is a function of the unknown variables of the algebraic loop.
36.2.5 Other Language Elements
The most basic Modelica language elements have been presented. Modelica additionally supports
enumerations as well as arrays and operations on arrays, for example,
parameter Real a[:]"Vector of coefficients";
final parameter Integer nx = size(a,1) - 1;
Real sigma[nx];
Real A[nx,nx] "System matrix";
equation
A = [zeros(nx-1,1), identity(nx-1);
-a[1:na-1]/a[na] ];
sigma = Modelica.Math.Matrices.singularValues(A);
The elements of arrays may be of the basic data types (Real, Integer, Boolean, and String) or in general
component models, e.g., a resistor. This allows convenient description of simple discretized partial dif-
ferential equations. Also mathematical functions without side effects can be defined. Functions may have
optional input and output arguments. External C- and Fortran subroutines can be called via this function
interface in a convenient way. A powerful package concept is available to structure large model libraries and
to find a component or/and a library in the file system giving its hierarchical Modelica class name due to a
name mapping of Modelica names to path names of the underlying operating system. Root level packages
may have a version number and scripts can be defined to perform automatic conversion between versions.
Instance and class definitions within a model may be replaceable and can be redeclared to another model
class in a higher hierarchy. This allows the substitution of complete submodels from a higher level, e.g., to
replace one controller or medium type by another one. Finally, a suite of annotations is standardized that
defines the graphical appearance of Modelica components, as well as annotations to define the details of
a parameter menu in a simple way. As an example, in Figure 36.10 the parameter menu of a revolute joint
is shown as it is automatically constructed by Dymola (Dynasim, 2006) from the Modelica definition.
36.3 Modelica Libraries
In order that the Modelica language is useful for modelers, it is important that libraries of the most
commonly used components are available, ready to use, and sharable between applications. For this
reason, the Modelica Association develops and maintains a growing Modelica Standard Library called
package Modelica. This is a free library that can be used in commercial Modelica simulation environments.
