Ferry M. Direct Stripcasting of Metals and Alloys: Processing, Microstructure and Properties
Подождите немного. Документ загружается.

Overview
of
solidification
processing
33
wall does
not
occur
and
Eq.
2.6
is applicable. For the special case
where
the
wetting angle is zero, there is
no
barrier to nucleation
and
solidification occurs
by
the direct
growth
of the solid into the melt. The process is often termed
epitaxial
growth
and
in
this case, the 'nucleus'
must
be
modelled
in
a different
manner to
that
just described (Porter
and
Easterling 1992) .
+
••••
w
••
• *
*.
....
.
..•.
..
s.
. .
.:
.•.
/:/
.........
.
. : -
..
....
\,
. .
~
~
~
.
~
.
••••
*.
r
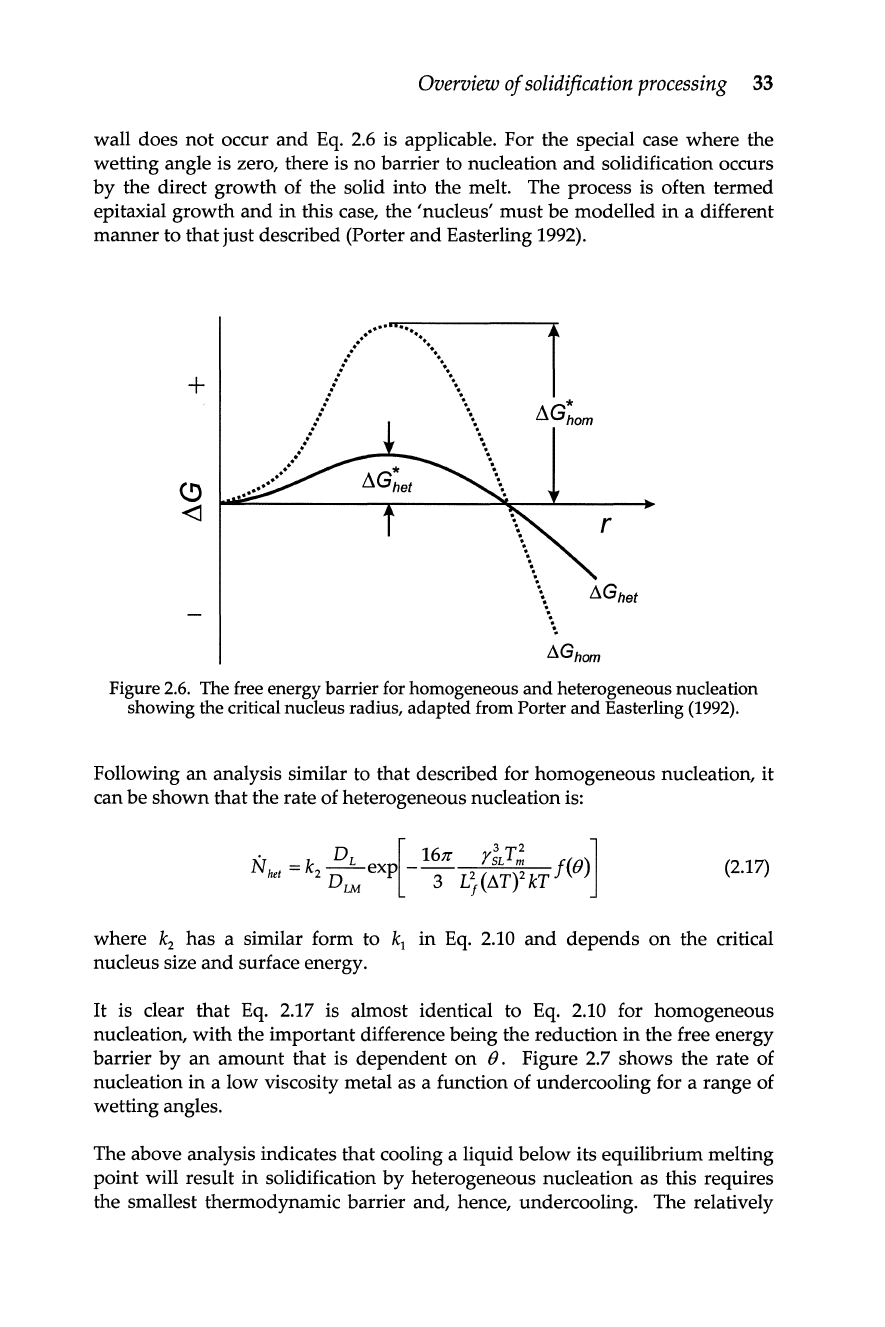
Figure
2.6.
The free energy barrier for homogeneous
and
heterogeneous nucleation
showing the critical nucleus radius, adapted from
Porter
and
Easterling
(1992).
Following
an
analysis similar to that described for homogeneous nucleation, it
can
be
shown
that the rate of heterogeneous nucleation is:
N - k D L ex
[_
16Jl'
r;L
T~
f«())]
he/ - 2
DLM
P 3
L~(~T)2
kT
(2.17)
where
k2
has a similar form to
kl
in
Eq.
2.10
and
depends
on
the critical
nucleus size
and
surface energy.
It
is clear
that
Eq. 2.17 is almost identical to Eq. 2.10 for homogeneous
nucleation,
with
the important difference being the reduction
in
the free energy
barrier
by
an
amount
that
is
dependent
on
(). Figure 2.7 shows the rate of
nucleation
in
a low viscosity metal as a function of undercooling for a range of
wetting angles.
The above analysis indicates
that
cooling a liquid below its equilibrium melting
point will result
in
solidification
by
heterogeneous nucleation as this requires
the smallest thermodynamic barrier and, hence, undercooling. The relatively

34
Direct
strip
casting
of
metals
and
alloys
simple analysis that generates
Eq.
2.17 has been extended to more complex
surface geometries of the mould or for the case of inoculating particles
(§2.2.1.3).
For example, if the mould contains surface irregularities such as local
pits or grooves, these are expected to alter nucleation behaviour appreciably. In
fact, the surface topography of the mould is exploited
in
the control of the
solidification microstructure during
DSC
(§5.3.2.1)
.
....
1----
Decreasing wetting
angle
I+-----+--
~
T"om-+----.
Undercooling
(~n
-+
Figure
2.7.
Rate of heterogeneous nucleation as a function of undercooling for a range
of wetting angles.
2.2.1.3 Factors affecting
nucleation
It
was shown in the previous section that nucleation usually occurs
at
low
undercootings on mould walls
and
impurity particles. Particles are often
introduced into the melt for the purpose of cast structure control
and
these are
termed nucleating agents or inoculants. The role of inoculation in cast structure
control is utilised
in
many alloy systems. For example, small quantities of Ti
and B
in
aluminium,
Zr
in magnesium, Fe
in
copper
and
TiN, TiO etc. in ferritic
iron will substantially increase the nucleation rate
and
refine the as-cast grain
size
by
up
to an order of magnitude.
With reference to
Eq.
2.16,
the activation barrier for nucleation is dependent
on
(), which is influenced
by
the surface energy
of
the solid-liquid interface. The
nucleation barrier is expected to disappear altogether
when
()
~
0,
i.e. when
the growing solid 'wets' the substrate.
An
effective inoculating agent must
therefore reduce
()
to a very small value which is usually achieved
by
good
planar lattice matching
(8<
10%) between the surfaces of the inoculant particle
and
the solidifying solid. This reduces substantially the particle-solid surface
energy and, hence, the undercooting required for nucleation (Figure
2.8).
An

Overview
of
solidification
processing
35
important example of inoculation is the use of TiN particles to refine delta-
ferrite in the weld metal zone of low alloyed steel.
If
these particles are
produced in the melt, the very low planar lattice disregistry
(£5
- 4%) between
{001}
planes of TiN
and
the
{001}
planes of the solidifying the phase markedly
reduces the energy barrier to nucleation. The effect of inoculation
by
Ti-rich
particles
on
solidification behaviour of ferritic stainless steel
during
DSC
is
discussed in §5.3.3.2. In the aluminium industry, grain refinement is
an
important aspect of direct chill casting (DCC) which is achieved
by
the addition
of 5%-Ti-I%B grain refiner to the melt to produce titanium boride
(TiB2)
particles (Greer
2003).
Recent investigations have shown that these particles
become
surrounded
by
a thin epitaxial layer of titanium aluminide (Ah
Ti)
which subsequently allows aluminium grains to nucleate
on
the
Ah
Ti
coating
of the
{QOOI}
basal faces of the particles. Excess titanium in the melt was found
to be important for effective grain refinement as
it
forms a thin layer of titanium
aluminide
on
the boride particles which nucleates aluminium crystals
by
a
peritectic reaction outside the bulk equilibrium concentration range
(Schumacher
2003).
It
is pertinent to note that while inoculation efficiency is qualitatively expected
from heterogeneous nucleation theory, the simple lattice mismatch theory
described here does
not
explain all observations.
An
important issue is the
surface geometry of the inoculating particles whereby surface roughness
or
pits
may
appreciably alter the nucleation behaviour (Porter
and
Easterling 1992).
10
3
10
2
g
g>
10
1
(5
0
e
Q)
10°
'U
I::
:::>
10'1
10'2
0
4 8
12 16
20
(hkl).
O(hkl)n
(%)
MnO
24
28
Figure
2.8.
The influence of degree of lattice matching between crystallographic planes
and
directions of bcc delta-ferrite
and
various types of particles
on
the undercooling
required for nucleation,
adapted
from Bramfitt (1969).

36
Direct
strip
casting
of
metals
and
alloys
2.2.2 Crystal growth beyond the nucleation stage
2.2.2.1 Morphology of the solid-liquid interface
Once nucleation has occurred, solidification proceeds
by
the migration of the
solid-liquid interface in a diffusion-controlled process. For the materials
discussed
in
this book, the interfacial structure is described as diffuse,
atomically rough or non-faceted
with
the transition from liquid to solid
occurring over several atom layers (Flemings 1974). This structure is in contrast
to that in various other materials such as polymers etc.
where
the transition
from solid to liquid occurs over a very narrow zone of order one atom layer.
These materials have atomically flat
or
faceted interfaces
with
the mechanism of
migration being somewhat different to that occurring
in
metals and, hence,
different types of solidification microstructures are usually generated
(Chalmers 1967; Chadwick
1972).
2.2.2.2 Interface
growth
kinetics
It
is
now
useful to determine the factors affecting the growth velocity of the
solid-liquid interface during solidification.
It
is assumed
that
the interface is
diffuse (metals) where atoms attach to the interface based
on
classical rate
theory (Flemings 1974). The solid-liquid interface velocity
(R)
of a
pure
metal
during
planar front growth is a function of the kinetic undercooling,
I1Tk
needed to drive the interface.
Therefore, if growth occurs
by
the movement of a planar interface, the interface
velocity
is:
(2.18)
where
k3
takes into account the addition of atoms to the solid-liquid interface
during
growth
and
the ratio
DL
/
DLM
is similar to that given in Eq. 2.10
and
indicates, for a viscous melt, a marked reduction in solidification rate
at
high
undercooling since
DL
«D
LM
•
However, solidification
by
dendritic growth is usually of
most
importance in
the various continuous casting processes (chapter
3).
For this growth
mode
it
is
more difficult to derive a growth rate equation
due
to morphological
considerations
and
thermal conditions
at
the growing dendrite tip (Minkoff
1986). Nevertheless, solutions of the dendrite tip velocity usually take the form:
(2.19)
where
k4
is a constant
and
p
an
exponent that is
dependent
on
the type of
model. Experimentally,
p can vary from
1.5
to 3 (Flemings 1974).
Overview
of
solidification
processing
37
2.2.2.3 Interface stability
in
pure
materials
In the case of a pure
metat
solidification is controlled
by
the rate of extraction
of the latent heat of fusion away from the solid-liquid interface. Taking the
simple case of unidirectional solidification, the interface moves
at
a velocity, R
( =
dx
/ dt ) into the liquid. The heat flow balance for this case is:
(2.20)
where
k,
and
kL
are the thermal conductivities of the solid
and
liquid,
respectively, and
G
s
(=
(dT/dx).) and G
L
(=
(dT/dx)L)
are the temperature
gradients
in
the solid
and
liquid, respectively.
/'
-
R
---+ ---+
III(
Heat
Flow
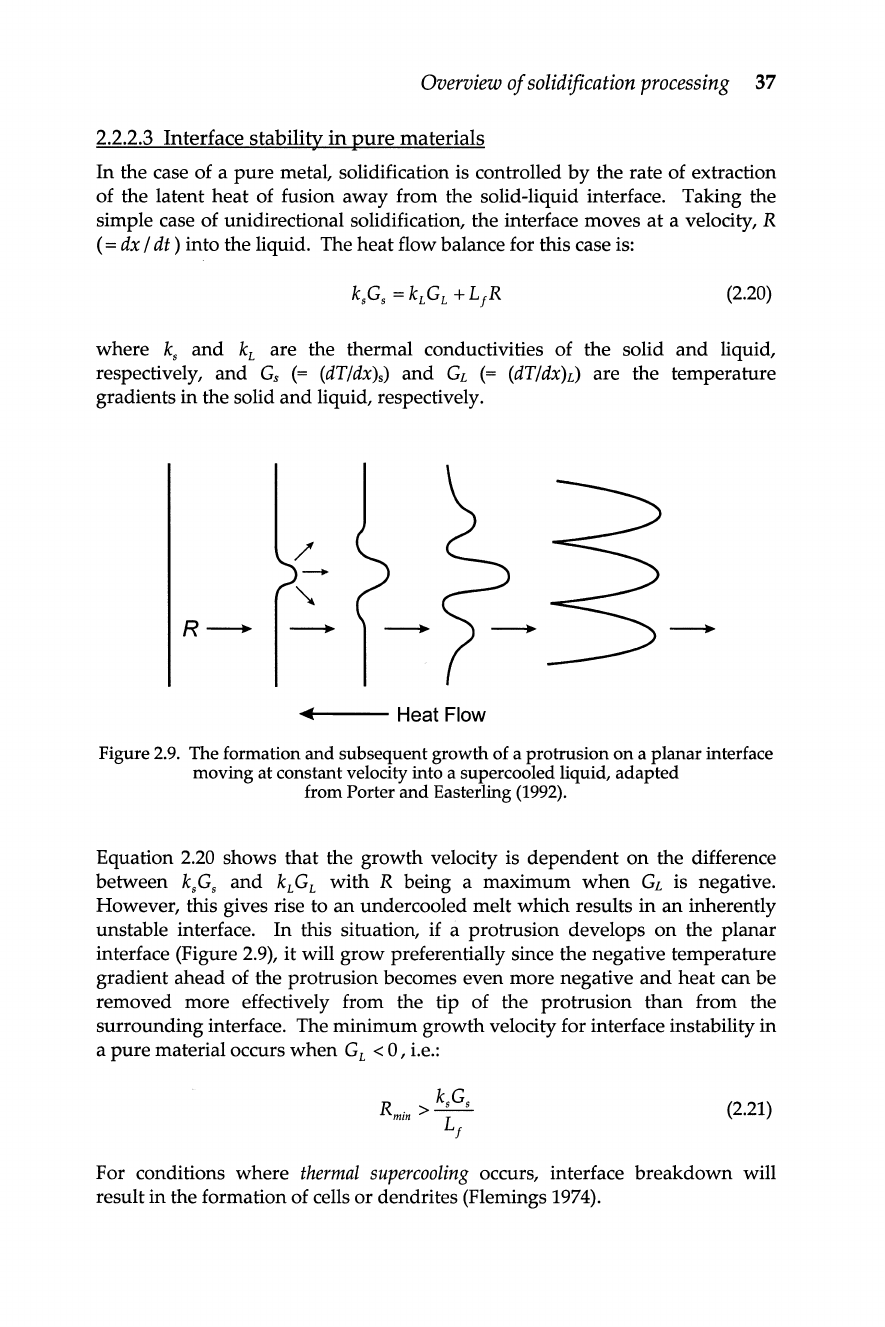
Figure
2.9.
The formation and subsequent growth of a protrusion
on
a planar interface
moving at constant velocity into a supercooled liquid, adapted
from Porter and Easterling
(1992).
Equation
2.20
shows that the growth velocity is dependent on the difference
between
k,G,
and
kLG
L
with R being a maximum when G
L
is negative.
However, this gives rise to
an
undercooled melt which results in an inherently
unstable interface. In this situation, if a protrusion develops on the planar
interface (Figure
2.9), it will grow preferentially since the negative temperature
gradient ahead of the protrusion becomes even more negative
and
heat can be
removed more effectively from the tip of the protrusion than from the
surrounding interface. The minimum growth velocity for interface instability
in
a pure material occurs when G
L
<
0,
i.e.:
(2.21)
For conditions where
thermal
supercooling
occurs, interface breakdown will
result in the formation of cells or dendrites (Flemings
1974).
38
Direct
strip
casting
of
metals
and
alloys
2.2.2.4 Interface stability
in
impure
materials
Theory
of constitutional
supercooling
An important aspect of DSC of alloys is the presence of impurities
and
alloying
elements in the melt. Hence, the solid-liquid interface
beyond
nucleation is
not
expected to be planar
and
grains will grow in a cellular
or
dendritic manner
due
to the phenomenon of
constitutional
supercooling.
In this section the
metallurgical conditions for constitutional supercooling in
an
ingot that is
solidifying initially
with
a planar growth front are discussed.
C
max
Colk
C
E
Composition
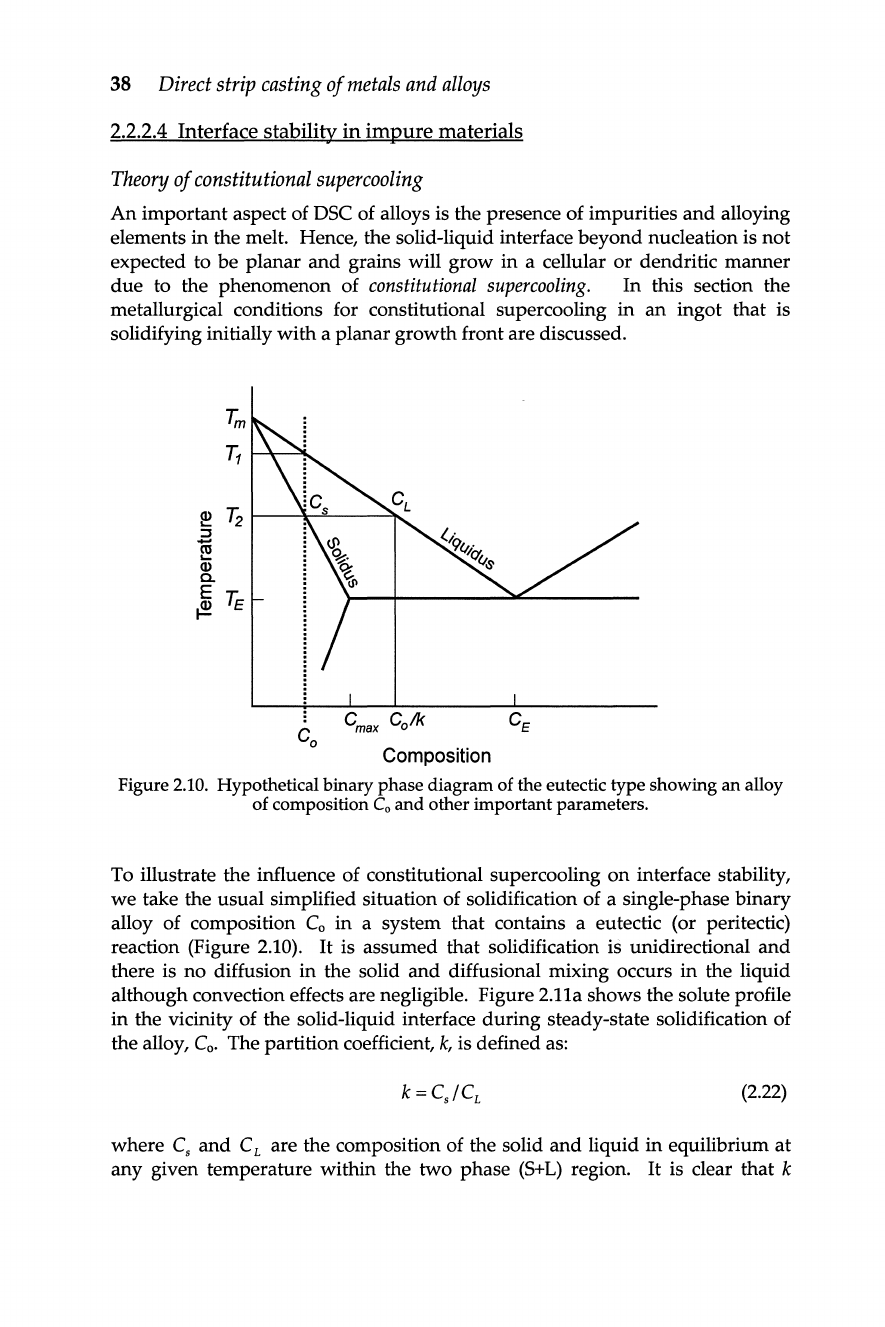
Figure 2.10. Hypothetical binary phase diagram of the eutectic type showing
an
alloy
of composition
Co
and
other important parameters.
To illustrate the influence of constitutional supercooling
on
interface stability,
we
take the usual simplified situation of solidification of a single-phase binary
alloy of composition
Co
in a system that contains a eutectic (or peritectic)
reaction (Figure 2.10).
It
is assumed that solidification is unidirectional
and
there is no diffusion in the solid
and
diffusional mixing occurs in the liquid
although convection effects are negligible. Figure 2.11a shows the solute profile
in the vicinity of the solid-liquid interface during steady-state solidification of
the alloy,
Co.
The partition coefficient,
k,
is defined as:
(2.22)
where C
s
and
CLare
the composition of the solid
and
liquid in equilibrium
at
any given temperature within the two phase
(S+L)
region.
It
is clear that k

Overview
of
solidification
processing
39
depends
on
the shape of the solidus
and
liquidus boundaries
with
k > 1 and k <
1 for a peritectic
and
eutectic reaction, respectively.
During steady-state solidification, the concentration of the solid is
Co
such that
solute is rejected into the liquid at the solid-liquid interface
and
is subsequently
transported away
by
diffusion. This condition generates the solute rich
boundary
layer ahead of the advancing interface in Figure 2.11a.
Due
to this
variation in solute concentration from
Colk
at
the interface to
Co
there is
an
increase in the liquidus temperature from
T2
to
TJI
as
shown
in Figure 2.11b.
Calk
c:
0
:;:::::;
·Cii
(a)
0
Cl.
E
8
Co
kC
o
T1
~
::::I
-
~
(].)
(b)
Cl.
E
~
72
Initial transient
Liquid
Constitutional
supercooled
region
x=O
Distance
(x)
Figure 2.11. Steady-state unidirectional solidification of the alloy,
Co'
in
Figure 2.10
growing
at
an
interface velocity,
R.
(a) Concentration distribution
and
(b) liquidus
temperature distribution ahead
of
the
solid-liquid interface. Superimposed
on
(b) are
two
thermal gradients in the liqUid
at
the S/L interface
showing
the region of constitutional supercooling.

40
Direct
strip
casting
of
metals
and
alloys
The concentration profile of the liquid can
now
be determined
by
solving the
following mass balance:
The amount of solute
rejected
by
the solid into the
liquid in the interface region
Amount of solute diffusing from
the interface into the liquid
down
a concentration gradient
This generates the following second order ordinary differential equation:
(2.23)
where x is the distance ahead of the interface
and
R is the velocity of the
solidifying growth front.
For the boundary conditions, C
L
=
Co
/ k
at
x = 0
and
C
L
=
Co
at
x =
00,
Eq.
2.23
can be solved analytically to generate the following relation (Flemings 1974):
(2.24)
Assuming a straight liquidus boundary
with
gradient, mu
and
a
pure
metal
melting temperature,
T
m,
the corresponding temperature profile of the liquidus
ahead of the interface
is:
(2.25)
The foregoing discussion assumes that only diffusional mixing occurs in the
liquid ahead of the solid-liquid interface. In most cases of alloy solidification,
convection is present
and
the concentration profile
may
be calculated using
Eq.
2.23
and
assuming a diffusional boundary layer of
width
0,
ahead of the
interface
and
C
L
=
Co
at
x = 0 (Burton
et
al.
1953).
Conditions
for
constitutional
supercooling
Stable plane front solidification is achieved
when
the interface is exactly
at
the
equilibrium temperature
and
every point in front of the interface is above
TL(x)
(dashed line
in
Figure
2.llb)
If
an instability (protrusion) forms
on
the flat
interface, it will find itself in a superheated region
and
will subsequently
remelt. However,
if
the liquid immediately ahead of the interface is
at
a
temperature below the equilibrium temperature, the liquid is supercooled
(dotted line in Figure 2.llb). Hence, if
an
instability (protrusion) forms on the
flat interface,
it
will
not
disappear since the peak of the protrusion will find
itself in a supercooled region. This situation is often termed
interface
breakdown
or
unstable
interface
growth.

Overview
of
solidification
processing
41
Assuming equilibrium
at
the interface, the critical condition for instability arises
when
the temperature gradient in the liquid is related to the concentration
gradient
by
the gradient of the liquidus line,
or
at
x =
0:
(2.26)
The initial solute gradient in the liquid
at
the interface
(x
=
0)
can be found
by
differentiating Eq.
2.24:
G~
=
(dC
L
)
=
RC
o
(~)
dx
x=o
DL k
(2.27)
The critical
temperatur~
gradient
at
the solid-liquid interface
is:
(2.28)
and
unstable interface growth is expected
when
the temperature gradient is less
than the right
hand
side of Eq.
2.28
(Tiller
et
al.
1953):
(2.29)
The left
hand
side of Eq.
2.29
can be rewritten as the ratio G
L
/
R which is an
important parameter for determining interface stability in
an
alloy
with
a large
number
of experiments verifying its validity (Flemings 1974).
If
the actual
temperature profile of the liquid falls below the equilibrium liquidus
temperature
due
to a high interface velocity, the liquid is constitutionally
supercooled. This usually occurs
under
normal conditions of industrial casting
of alloys
and
invariably leads to cellular or dendritic
growth
(§2.2.2.2).
Figure
2.12
is a schematic diagram showing the expected conditions that lead to
the formation of planar, cellular or dendritic structures.
It
can be seen that the
first type of instability is cellular growth which occurs
when
Eq. 2.29 is satisfied.
There is a gradual transition from cellular to dendritic solidification in most
alloys
with
the latter expected when (Kurz
and
Fisher 1981):
(2.30)
The growth condition given
by
Eq.
2.30
is expected for rapid solidification
processes such as DSC (§3.2.3).

42
Direct
strip
casting
of
metals
and
alloys
RL
Figure
2.12
. Schematic diagram showing the G
L
-
RL
combination that favours planar,
cellular or dendritic solidification
in
weld metal, after Grong (1994) (with kind
permission
of
Institute
of
Materials, Minerals and Mining, UK).
Other
interface
stability
theories
The foregoing analysis is oversimplified
and
more advanced treatments of
interface stability have been proposed, see
e.g.
Mullins
and
Sekerka (1963, 1964)
and
Trivedi
and
Kurz (1986). While a rigorous treatment of the Mullins-
Sekerka theory is beyond the scope of this book, a semi-quantitative
explanation is possible. The theory considers a small perturbation
on
a planar
interface
and
determines the conditions
at
which the perturbation either grows
(unstable interface)
or
decays (stable interface), Figure 2.13. Whether the
perturbation continues to grow is dependent
on
the interaction of the thermal
and
solute fields,
on
solid-liquid interfacial energy
and
interface kinetics.
The Mullins-Sekerka theory can be used to predict the conditions for interface
instability and the wavelength of the fastest growing instabilities. The
sinusoidal perturbation of the interface in Figure
2.13 is given by:
z =
o(t)Sine~)
(2.31)
where A
and
oCt)
are the wavelength
and
amplitude of the perturbation,
respectively, at time,
t.
The time dependence of the amplitude of the perturbation
in
Figure
2.13
(J
= do /
dt)
can be calculated during interface movement
in
the x direction
using Eq.
2.31
and
by
solving the following series of differential equations that
