Faulon J.L., Bender A. Handbook of Chemoinformatics Algorithms

Подождите немного. Документ загружается.

278 Handbook of Chemoinformatics Algorithms

up to this point might be identified here and that structure discarded from the list of

potential CAMD candidate solutions.

9.4.1.3 Postdesign Phase

When candidate solutions make it through the design phase, additional analysis is

required to determine if they are suitable compounds to solve the problem at hand.

Issues such as price, availability, ease of synthesis, and potential environmental impact

are just a few of the factors that might preclude a compound for further consideration.

Additionally, some design constraints may not have been accessible through modeling

and, thus, experimentation is required to determine these properties (or confirm some

of the previously predicted properties inside the CAMD algorithm).

9.4.2 CASE STUDY:CHEMICAL PROCESS INDUSTRY APPLICATION

As previously mentioned, the Hybrid-CAMD algorithm is implemented in the soft-

ware package ProCAMD, which is a tool within ICAS. Several case studies have been

presented and suggested [15]; we describe one here [7,49].

3-Octanol is oxidized to 3-octanone in the solvent dichloromethane. However,

while this solvent has many favorable properties, it is not a green solvent (it has a

nonzero ozone-depletion potential) and, thus, a replacement is warranted.

The desired list of properties for a replacement solvent includes

• Melting point <250 K

• Boiling point <380 K

• Hildebrand solubility parameter between 17 and 19 MPa

1/2

• Liquid density at 298 K between 0.95 and 1.05 g/cm

• log P < 2

• log LC

< 3

• ODP and GWP should be low

• Solvent–solute solubility should be high

• Solvent–water should be immiscible

Implementing the Hybrid-CAMD algorithm, it was found that 4936 compounds

(which include isomers) were generated with 215 of those satisfying all of the property

constraints. The authors report that some of these compounds include 2-pentanone,

sec-butyl acetate, 2-oxepanone, γ-valerolactone, and 2-ethoxy ethylacetate, with the

first compound being the most environment friendly (Figure 9.1).

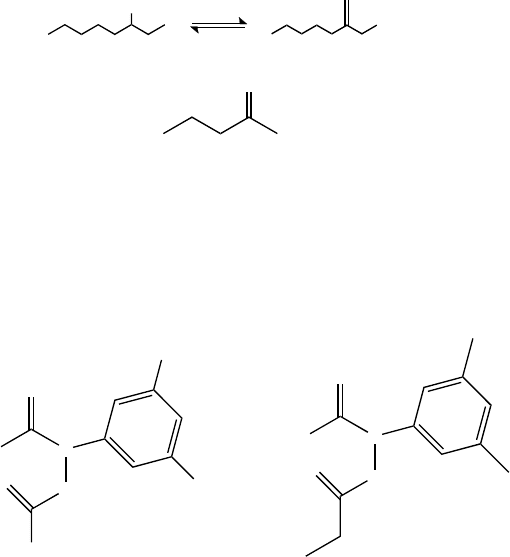
9.4.3 CASE STUDY:BIO-RELATED APPLICATION

Gani reports on a case study to design active herbicides with the α-choloroacetamideo-

chloroacetanilide backbone [15]. Based on a QSAR where log P was an independent

variable, potential candidates were screened based on activity (by first estimating

log P) and the most active compound was found. The backbone structure had three

substituent points and the solution with the highest activity is presented in Figure 9.2.

Computer-Aided Molecular Design 279

Octan-3-ol Octan-3-one

Pentan-2-one

FIGURE 9.1 Using the Hyper CAMD algorithm, pentan-2-one is among the best solvents

predicted to replace dichloromethane for the oxidation of octan-3-ol. (From Gani, R., C.

Jimenez-Gonzalez, and D.J.C. Constable, Comput. Chem. Eng., 2005, 29: 1661–1676. With

α-Chloroacetamideo-chloroacetanilide

backbone

Optimal structure

FIGURE 9.2 The template compound and the predicted optimally active structure.

9.5 CAMD AS OPTIMIZATION

Since the goal of CAMD is to build a molecule (or set of molecules) that has a certain

property (or range of properties), this can be considered an optimization problem since

one can attempt to minimize the difference between the desired and the predicted

property. Couched in this fashion, techniques from optimization theory have been

brought to bear for use within CAMD. Such approaches were initiated in the 1990s

[50,51] and the first optimization attempt to use a connectivity index was reported by

1998 by Raman and Maranas [16].

In general, the CAMD as an optimization approach is to formulate the objective

function using the desired properties while incorporating constraints on the structures

that can be created. This falls under the wide category of mixed-integer nonlinear

programs (MINLP), which are then solved using any of a variety of optimization

codes designed for MINLP problems. As an illustration of such an approach, we

describe the algorithm behind solving an MILP problem using connectivity indices,

although other approaches exist [52,53].

280 Handbook of Chemoinformatics Algorithms

9.5.1 MIXED-INTEGER LINEAR PROGRAMMING ALGORITHM FOR CAMD

Camarda and Sunderesan recently solved an optimization problem related to design-

ing valued-added soybean oil products [17]. They used an MILP approach in

conjunction with order 0, 1, and 2 (simple and valence) connectivity indices [54]. The

key step in their approach was the use of binary variables that allowed them to rewrite

the connectivity indices in terms of these variables. In their formulation, molecules

were represented by a partitioned adjacency matrix that describes the connectivity

of prespecified groups within a molecule (they had chosen 16 groups). The binary

variables, in turn, were related to entries in the partitioned adjacency matrix. This,

in conjunction with a Glover transformation, created objective function expressions

that were linear and, accordingly, easier to solve.

9.5.1.1 Molecular Representation

To represent a molecule, the data structure required is one that identifies whether

a particular group is present within a molecule, what other group(s) it is bonded

to and the multiplicity of that particular bond. What is used is two sets of binary

variables (re: 0 for absence; 1 for presence): W (which determines the presence or

absence of a group) and A (which determines connectivity and bond multiplicity).

Required a priori is a listing of groups to be used and their maximum occurrence

number in a molecule. For example [55], we can examine the binary variables W and

A for the molecule propane. Here, three basic groups are listed with their allowed

multiplicity given parenthetically: CH

(3), CH

(3), and CH (2). Accordingly, an

adjacency matrix can be written, but in this approach it is partitioned to cluster

the same groups together, resulting in a structure called a partitioned adjacency

matrix (A). We show the partitioned adjacency matrix for propane using the three

basic groups with allowed multiplicity for bond multiplicity 1 in Figure 9.3. Note

that similar matrices will exist for bond multiplicity 2 and 3, yet those will have

zero values for all elements in this instance since propane has no double or triple

bonds.

Since propane has two CH

groups, the first one is labeled “1,” while the sec-

ond one is labeled “2.” Such a labeling refers to the row/column in the partitioned

adjacency matrix. Likewise, the single CH

group in propane is labeled “6.” Note

that the other group available, CH, is not present in propane and has zeros for all

entries.

Now that the bonding has been accounted for using the partitioned adjacency

matrix, the presence and absence of a group is provided in an existence vector, W.In

this example, W would be the vector: W ={1, 1, 0, 0, 0, 1, 0, 0} where the labeling

mentioned previously is retained here. Once the binary variables A and W are written,

expressions for the molecular connectivity indices (both simple and valence) can be

given in terms of these variables.

9.5.1.2 Constraint Equations

With regard to constraints, molecular feasibility expressions based on the valence of

basic groups were written in terms of the binary variables. Additional expressions

Computer-Aided Molecular Design 281

limit the number of basic groups in a molecule as well as the number and types of

rings in a molecule. In order to guarantee that molecules are fully connected, network

flow constraints [56] are written in terms of the binary variables using sink and source

nodes.

ALGORITHM 9.6 MILP ALGORITHM FOR CAMD

1. Select basic groups

2. Create linear QSARs using connectivity indices for properties of interest

3. Set target values for properties of interest

4. Write objective function in terms of minimizing absolute value of difference

between QSAR prediction and target value for all properties

5. Write all constraint equations in terms of binary variables

6. Solve MILP design problem and arrive at optimal solution

The authors also allowed the use of an integer-cut equation as well in the solution

to the problem (not listed above in the algorithm) in order to make previously arrived

at solutions infeasible within the algorithm. This provided “ranked” solutions rather

than just a single optimal solution.

Note that the solutions to this problem are in terms of binary variables which, in

turn, are related to the entries of the partitioned adjacency matrix. The authors restrict

their solution space through the use of templating, which, in essence, preassigns parts

of the partitioned adjacency matrix such that a portion (or most) of the structure

is already set prior to solving the problem. This is done because of the complexity

of the problem and the computational resources required, even after linearization.

123456

0000010

0000000

1100000

0000000

00000000

FIGURE 9.3 The partitioned adjacency matrix for propane with bond multiplicity of 1.

(Reprinted from Siddhaye, S. et al., Comput. Chem. Eng., 2004, 28: 425–434. With permission.

282 Handbook of Chemoinformatics Algorithms

—(CH

)

—CH

—

CH—(CH

)

—N

Template

—(CH

)

—CH

—

CH—(CH

)

—N

—CH

—O—CH

—

—CH

—O—CH

—

—CH

—O—CH

—CH

—OH

—CH

—O—CH

—CH

—OH

Optimal solution

FIGURE 9.4 Starting with a template, an optimal structure was found by the MILP algorithm

which is predicted to possess the required properties. (Reprinted from Camarda, K. and P.

American Chemical Society.)

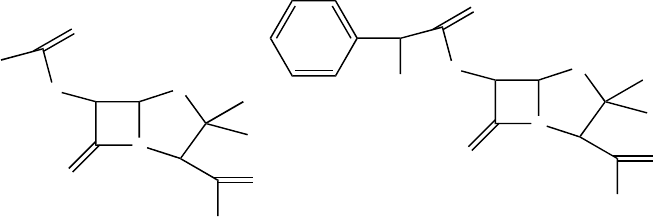
9.5.1.3 Case Study

Chemical process industry application: Camarda and Sunderesan provide a few

examples of the implementation of this algorithm as applied to soybean oil prod-

ucts. Here, we describe the design of a fuel additive. The desired properties are as

follows:

• Hydrophilic–lipophilic balance, HLB = 8

• Lubricity between 2.0 and 3.75 N/kg

• Critical micelle concentration value between 10

−1

and 10

−5

mol/L

The base groups used were C, CH, C

CH, CH

, NH, OH, NO

,CH

O, and N, with normal valency for each implied. QSARs were created using both

simple and valence connectivity indices, up to order 2. The problem was solved

using CPLEX 6.5 (a mixed-integer optimizer available from ILOG, Inc.) accessed

through the GeneralAlgebraic Modeling System on a SUN Ultra 10. Using a template

(Figure 9.4), the optimal solution was found in approximately 1.5 h.

The optimal structure had a predicted HLB of 7.9, a CMC of 10

−3

mol/L, and a

lubricity of 3.6 N/kg.

9.5.1.4 Case Study: Bio-Related Application

Camarda and coworkers used the MILP formulation for pharmaceutical product

design [55]. In one example, starting with a penicillin backbone, their goal was to find

the optimum compound that possessed a log P value closest to 0.35 and a melting

point closest to 127

◦

C. The base groups used were C, CH,

CH, CH2, NH, OH, CH3,

O, O, and F, with normal valency for each implied. QSARs were created using both

simple and valence connectivity indices, up to order 1. The problem was solved using

CPLEX 6.5 (a mixed-integer optimizer available from ILOG, Inc.) accessed through

the General Algebraic Modeling System on a SUN Ultra 10. The best solution was

found in 277 s of CPU time, which is provided in Figure 9.5 along with the template.

Computer-Aided Molecular Design 283

Template

Optimal solution

FIGURE 9.5 Starting with a template common to all penicillins, an optimal structure was

found by the MILP algorithm which is predicted to possess the required properties. (Reprinted

from Siddhaye, S. et al., Comput. Chem. Eng., 2004, 28: 425–434. With permission. Copyright

2004 Elsevier.)

The optimal structure had a predicted log P value of 0.347 and a melting point of

128

◦

9.5.2 CAMD USING SIGNATURE

In the mid-1990s, Faulon introduced the Signature molecular descriptor to elucidate

structure [57,58], and in the early part of this decade, Faulon and Visco combined

Signature with a structure generation code for use in inverse design [19,59,60]. Theirs

is an approach that sits somewhere between the CAMD methodology of Gani and

that of inverse QSAR. They use a fragmental descriptor, called Signature, and have

developed structural constraint and valence equations associated with the presence of

these fragments in a molecule. This sets up a series of Diophantine equations that are

solved, and then the solutions are filtered through scoring QSARs to arrive at optimal

candidates. 2D structures are then generated from these solutions using an in-house

code that implements an enumeration algorithm [19,57].

9.5.2.1 What Is Signature?

In the previous two algorithms discussed in this chapter (and, in fact, most CAMD

algorithms), predetermined groups are the building blocks to make molecules. These

groups can either be self-selected or come from a standard list to facilitate group-

contribution techniques, such as the UNIFAC groups [26]. Signature, on the other

hand, is a more formalized and systematic approach to generate groups [59].

In order to facilitate a description of CAMD using Signature, we briefly describe

the Signature molecular descriptor, although a formal definition is given in Chapter

3. An atomic Signature is a rooted tree of a 2D description of a molecule that spans

the local environment around the root. The height of the atomic Signature indicates

the path-length from the root atom. Height-0 is just the atom (or root), height-1 is the

atom and its neighbors away by one path-length, etc. No backtracking is allowed in

the creation of atomic Signatures [59]. In this formalism, a molecule of n atoms has

n atomic Signatures. The molecular Signature of a molecule is then the sum of its

284 Handbook of Chemoinformatics Algorithms

Root atom

Height 0 C

Height 1 C ( =C H H)

Height 2 C ( =C (O H) H H)

Height 3 C ( =C (O (H) H ) H H)

(a)

(b)

C( =C H H ) + C ( =C O H) + O ( C H) + 3 H (C) + H (O)

FIGURE 9.6 (a) The atomic Signatures at four heights for one of the carbon atoms in ethenol.

(b) The molecular Signature for ethenol at height-1.

atomic Signatures, with coefficients on each atomic Signature signifying the number

of occurrences of that atomic Signature in a molecule.

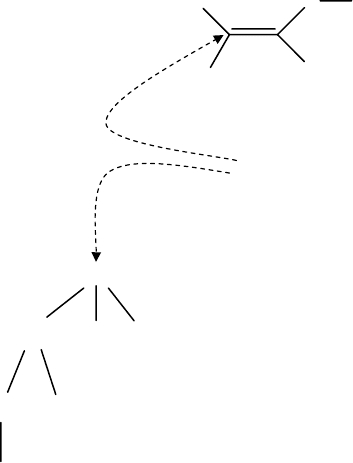
For example, let us consider the 2D graph of ethenol. The dashed arrow identifies

one of the carbon atoms for which we will write the atomic signatures of various

heights. Since there are seven atoms in ethenol, there are seven atomic Signatures

at each height. After writing all of the seven atomic Signatures for ethenol at, say,

height-1, their sum would be the molecular Signature at height-1. Note that all seven

of the height-1 atomic Signatures for ethenol are not unique; their degeneracies are

noted by the coefficients in the molecular Signature. This is shown in Figure 9.6.

The types of bonding between atoms in the Signatures are denoted in the atomic

Signature itself (as seen in Figure 9.6) and can account for bonding in aromatic rings

as well.Also note that various valence states are accounted for through different vertex

labeling, such as with nitrogen or phosphorus.

Computer-Aided Molecular Design 285

9.5.2.2 Inverse Design Algorithm Using Signature

Inverse design using Signature can be divided into a four-step process: (1) making

the atomic Signature database, (2) solving the atomic Signature constraint equations,

(3) solution evaluation, and (4) structure generation and analysis [18,61]. We discuss

each step in the next section and provide the appropriate algorithm for that step.

9.5.2.2.1 Making the Atomic Signature Database

Unlike the selection of tabulated fragments discussed in the previous two methods,

the Signature approach requires the identification of a particular dataset to work from.

The normal procedure is to use a dataset for which you have generated a QSAR for a

property (or properties) of interest. Once a dataset is selected, a specific atomic Sig-

nature height is chosen for the problem. If a small height is used (say height-0), the

building blocks are just the elements that appear in the dataset. If a large height is cho-

sen (say height-4), the building blocks are height-4 atomic Signatures, of which there

would be many for a given system. A dataset of 100 compounds might produce hun-

dreds of height-4 atomic Signatures. Thus, the selection of an atomic Signature height

controls the number and type of fragments used to make the molecules. Traditionally,

height-1 or height-2 has been used in inverse design problems using Signature, which

provides a convenient trade-off between a too general atomic Signature (low height)

and a too specific atomic Signature (high height) [5].

To convert 2D structures into its Signature representation requires the use of a

freely available translator code [62]. Structures are input in a common form (such as

an MDL mol file) and the molecular Signature of a compound is generated. This

information is parsed to develop a list of unique atomic Signatures at a desired

height.

ALGORITHM 9.7 INVERSE DESIGN WITH SIGNATURE:

GENERATING ATOMIC SIGNATURE DATABASE

1. Select particular dataset of interest

2. Select desired atomic Signature height

3. Run Signature translator code on 2-D structure files

4. Generate list of unique atomic Signatures at pre- selected height

The list of atomic signatures obtained at this step forms the set of fragments from

which new and/or novel structures will be generated.

9.5.2.2.2 Solving the Atomic Signature Constraint Equations

In order to make solutions from the atomic Signatures, theymust be connected together

in a way that satisfies valency and connectivity constraints. The necessary condition to

create a connected graph using Signature is called the graphicality equation and there

is but one equation per dataset. This expression is based simply on known valences

for the various atoms (and their types) in the dataset and is given by the following

286 Handbook of Chemoinformatics Algorithms

modulus expression

Mod





i=2

(i −2)n

−n

+2, 0



= 0,

where z is the maximum number of vertices of atoms in the dataset while n

is the

degree of the root of signature i [18].

The other system constraints on the atomic Signatures are related to the bonding

that occurs in a Signature. For example, consider propane, whose atomic Signatures

at height-1 (and the degeneracy of occurrence) is shown in Table 9.1.

Here, there are two types of bonds: a carbon bonded to another carbon and a carbon

bonded to a hydrogen. Let us examine the carbon–hydrogen bonding first. The first

height-1 atomic signature (x1) contributes two C

−

H bonds while the second height-1

atomic signature (x2) contributes three C

−

H bonds. The third atomic signature (x3)

contributes one H

−

C bond. Since the number of C

−

H bonds has to equal the number

of H

−

C bonds, the constraint equation would be: 2x1 +3x2 −x3 = 0

When working with bonds between the same atom type, such as carbon–carbon,

a similar approach is used. Here, x1 contributes 2 carbon–carbon bonds, while x2

contributes 1 carbon–carbon bond. However, an equality constraint (as in the C

−

bond example) would be unnecessarily strong here, since the atom types are the same.

Accordingly, the sum of the contributions from each atomic signature with a C

−

bond would need to be an even number. Thus, the constraint equation for the C

−

bond would be: Mod(2x1 +x2, 2) = 0. Note, finally, that the graphicality equation

here becomes Mod(2x1 +2x2 −x3 + 2, 2) = 0. The reader can use the occurrence

numbers in Table 9.1 to verify the equations [63].

Practically, instead of three equations (as in the example above) to be solved,

many (dozens) of equations are the norm for reasonable-sized datasets with a variety

of atom types. The constraint equations form a set of Diophantine equations since

they involve integer coefficients and require integer solutions. While generic solvers

exist for these types of systems [64], the most recent use within the larger CAMD

approach with Signature uses an efficient brute force approach that iterates over the

range of values of the variables in the dataset [65]. It is efficient since it starts with

the least complex variables (fewest iterations) and significantly saves computational

time by omitting the portion of the solution space that does not satisfy any single

equation.

TABLE 9.1

Height-1 Atomic Signatures for Propane

Signature Variable Occurrence

[C]([C][C][H][H]) x11

[C]([C][H][H][H]) x22

[H]([C]) x38

Computer-Aided Molecular Design 287

ALGORITHM 9.8 INVERSE DESIGN WITH SIGNATURE: SOLVING

THE CONSTRAINT EQUATIONS

1. Generate all constraint equations to form set of Diophantine equations

2. Determine min and max values of occurrence numbers of each atomic

signature in the dataset

3. Run efficient brute force algorithm to solve Diophantine equations

The solution to even moderate-sized problems can cause both storage and time

concerns. It is not uncommon to generate millions or evenbillions of solutions [61,63].

One can place scoring functions or other filtering expressions inside the brute force

algorithm to mitigate issues of storage, as needed.

9.5.2.2.3 Solution Evaluation

Once the solutions have been generated, they need to be evaluated for fitness. At

this point (or earlier) a QSAR would be generated based on data available and using

the occurrences of the atomic signatures as independent variables. Multiple QSARs

can be generated and they would be used (in succession) to identify those candidates

that satisfy target values (or ranges). The equations need not be linear. Constraints

on the number of allowed rings in the system can be applied at this point as well.

Additionally, other input can be used here to score the solutions, such as the Lipinski’s

Rule of 5 if working on pharmaceuticals [66].

ALGORITHM 9.9 INVERSE DESIGN WITH SIGNATURE: SOLUTION

EVALUATION

1. Develop QSARs for properties of interest using atomic signatures as

independent variables

2. Screen candidate solutions through QSARs and save those solutions which

possess desired predicted property values

3. Set min/max desired cycles in candidate solutions and screen solutions passing

through step 2 with cycle filter

4. Screen candidate solutions passing through step 3 with additional filters

relevant to problem

9.5.2.2.4 Structure Generation and Analysis

Once the solutions (re: a molecular Signature) have passed through the various scor-

ing routines, they are ready to be turned into 2D structures. There is a degeneracy

associated with going from a molecular Signature to a 2D structure. At small heights,

the degeneracy is quite large, but monotonically decreases with Signature height until

there is a unique 2D structure associated with a particular molecular signature. This

occurs quite rapidly and most molecular Signatures are basically nondegenerate at

height-3 [19,67].

Structure generation is performed using an algorithm developed by Faulon and

coworkers [19], based on an earlier isomer enumeration algorithm developed by

Faulon [58,68]. The algorithm is iterative and involves starting with a molecular

Signature of all atoms and no bonds and then attempts to add bonds in all possible