Фарзане Н.Г., Илясов Л.В. Технологические измерения и приборы

Подождите немного. Документ загружается.

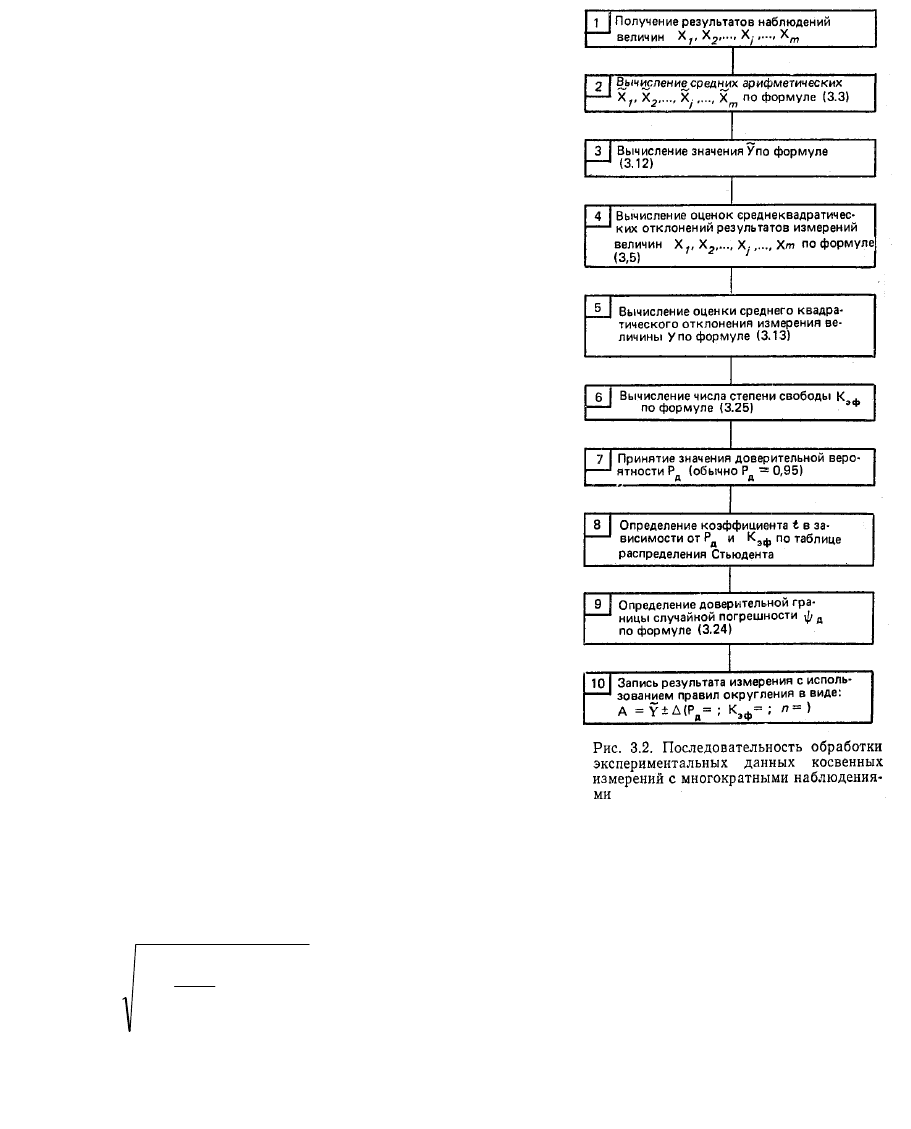
Последовательность обработки

экспериментальных данных косвенных

измерений с многократными наблюдениями для

некоррелированных величин приведена на рис.

3.2. Эта последовательность предусматривает,

что для аргументов, получаемых путем прямых

измерений, справедливы все

предположения, изложенные в § 3.4. На

рис. 3.2 в п. 10 записана погрешность Δ вместо

, так как предполагается, что систематические

погрешности полностью исключены. Число п

указано, для того аргумента при измерении

которого выполнено наименьшее число наблю-

дений. Для случая, когда значениями

неисключенных систематических погрешностей

нельзя пренебречь, разработана методика оценки

суммарной погрешности [29], близкая к ранее

приведенной для прямого измерения с

многократным наблюдениями.

При определении погрешности косвенного

измерения важными являются установление

частных погрешностей, которые в основном

определяют погрешность косвенного измерения,

и исключения из рассмотрения тех

погрешностей, которые не оказывают на общую

погрешность почти никакого влияния.

Определение последних связано с процедурой

округления результата измерения и оценки погрешности.

Если в выражении (3.13) какая-либо частная погрешность такова, что

выполняется условие

∑

≠













∂

)

(05.1)

(

(3.26)

то этой частной погрешностью

можно пренебречь, так как при округлении уже число 1,0499... принимается за

1,0.

Из выражения (3.26) можно получить формулу [9] для вычисления k-й

частной погрешности:

)

(3.0)

()/( YSXSXf

<∂∂

(3.27)

Это выражение называют критерием ничтожности погрешности. По-

грешности, отвечающие этому критерию, называют ничтожными или

ничтожно малыми, поэтому их не принимают во внимание при вычислении

общей оценки погрешности косвенного измерения.

§ 3.6. Оценивание результатов и погрешностей совокупных и

совместных измерений е многократными наблюдениями

В § 1.2 отмечалось, что при совокупных и совместных измерениях

искомые величины находят из решения системы уравнений (1.7), которая

связывает их с величинами, непосредственно измеряемыми. При этом

измерения осуществляются так, что получаемое число уравнений превышает

число искомых переменных. Для этого проводят многократные наблюдения

одних и тех же физических величин в одинаковых или различных условиях (в

зависимости от конкретной задачи). Результаты наблюдений для всех

измеряемых в каждом эксперименте величин могут быть обработаны методами,

изложенными в § 3.4, 3.5, а затем их результаты могут быть сгруппированы в

систему уравнений, из решения которой могут быть найдены m физических

величин, определяемых совокупными или совместными измерениями. Оценка

значений этих m величин и их погрешностей при этом можно найти так же, как

и для косвенных измерений.

В настоящее время для обработки экспериментальных данных при

выполнении совместных и совокупных измерений в большинстве случаев

применяют метод Лежандра, называемый методом наименьших квадратов.

Сущность этого метода состоит в следующем. Если в систему уравнений

(1.7), записанную для краткости в виде

F(Х

, Х

, ..., Х

, Y

, ..., Y

)=0

(i=1,2,…, n)

(3.28)

подставить значения величин Х

, Х

, ..., Х

, полученных как результаты

наблюдений, то систему уравнений (3.28) можно преобразовать следующим

образом:

F(Y

, Y

, ...,Y

, …, Y

)=0 (i=1,2,…, n) (3.29)

Эта система содержит только искомые физические величины и

постоянные коэффициенты. Число п равно общему числу наблюдений

измеряемых величин X

(в том числе результаты повторных наблюдений одной

и той же величины). Из-за ограниченной точности измерений величин X

при

числе наблюдений п, существенно большем числа неизвестных т, не

представляется возможным найти такие значения неизвестных Y

, при которых

выполнялись бы все уравнения полученной системы. Поэтому задача сводится

к нахождению для искомых величин Y

их оценок

, представляющих собой

наилучшие приближения к истинным значениям. Уравнения (3.29) в отличие от

обычных математических уравнений принято называть условными, так как

подстановка в них найденных каким-либо путем значений оценок

не

обращает уравнение в нуль:

0)Y

..., ,Y

,,Y

(

mj21

≠… (i=1,2,…, n)

(3.30)

Чтобы эти уравнения превратились в тождества, их следует записать в

виде

0)Y

..., ,Y

,,Y

(

mj21

=+…

υ (i=1,2,…, n)

(3.31)

Величины v

принято называть невязками, или остаточными, по-

грешностями уравнений.

Согласно методу наименьших квадратов, наилучшие оценки величин

могут быть найдены в том случае, если функция Ω, представляющая собой

сумму квадратов остаточных погрешностей условных уравнений, будет

минимальна:

min

==Ω

∑

(3.32)

Суть метода наименьших квадратов

может быть уяснена при рассмотрении

определения параметров а и b линейной за-

висимости ξ==аφ + b. Пусть в результате

экспериментальных исследований найдены

пары значений ξ

и φ

(рис. 3.3).

В соответствии с методом наименьших

квадратов для прямой, наилучшим образом

проходящей относительно всех n точек,

полученных в результате экспериментальных исследований значения, а и

bдолжны быть выбраны такими, чтобы функция

∑

=Ω

υ была минимальна.

Рассмотрим теперь последовательность обработки экспериментальных

данных совокупных или совместных измерений для наиболее

более важного случая, когда в систему (1.7) входят только линейные

независимые уравнения:











+++=

mnmnnn

YkYkYkX

...

.................................................

...

2211

22221212

12121111

(3.33)

где X

(i=l, 2, ..., n) —результаты наблюдений измеряемых физических величин;

— известные коэффициенты; Y

(j=1, 2, ..., m) — искомые физические

величины. Результаты наблюдений величины X

— исправлены, равнорассеяны,

некоррелированы и подчиняются нормальному закону распределения. Систему

(3.33) можно записать в виде

∑

jiji

YkX

(i=l, 2, ..., n)

(3.34)

Если коэффициенты k

,- в уравнениях (3.33) определены с такой малой

погрешностью, что по сравнению с погрешностями измерений величин X

ими

можно пренебречь, то уравнение (3.33) считают точным.

Так как результаты наблюдений X

содержат погрешность, то по аналогии

с (3.31) для системы (3.34) запишем:

∑

ijiji

YkX

υ (i=l, 2, ..., m)

(3.35)

Для каждой остаточной погрешности

∑

−=

jijii

YkX

(3.36)

Тогда для суммы квадратов остаточных погрешностей имеем

∑ ∑∑

= ==













−==Ω

jiji

YkX

min

(3.37)

Для определения

, удовлетворяющих условию (3.37), находят все

частные производные функции Ω по Y

, приравнивают их к нулю и получают

тем самым новую систему из т уравнений:

1 1













−−=

∂

Ω∂

∑ ∑

= =

jiji

kYkX

(j=l, 2, ..., m)

(3.38)

или

1 1













−

∑ ∑

= =

jiji

kYkX (j=l, 2, ..., m)

(3.39)

Эта система является линейной относительно искомых величин

. Ее

называют системой нормальных уравнений. Число этих уравнений всегда равно

числу неизвестных величин Y

. Для упрощения написания системы нормальных

уравнений пользуются обозначениями Гаусса для сумм:

[ ]











∑

jiij

ljilij

jjij

XkXk

kkkk

kkk

1,2,...m)(l

(3.40)

Для рассматриваемого случая система нормальных уравнений имеет вид:

[

]

[

]

[

]

[

]

[ ] [ ] [ ] [ ]











=+++

XkYkkYkkYkk

mmmmmm

...

.................................................

...

2211

22222112

11221111

(3.41)

Решение системы (3.41) находят с помощью определителей для каждой из

искомых величин:

DDY

(3.42)

где

[

]

[

]

[

]

[ ][ ][ ]

[

]

[

]

[

]

[ ][ ][ ]

mmmm

kkXkkk

kkkkkk

......

.....................................

......

.....................................

......

2212

1111

22212

12111

Определитель D

получен заменой в определителе D j-го столбца

столбцом свободных членов (3.41).

Получение оценок искомых величин связано с большим объемом

вычислений. Причем объем вычислений быстро увеличивается с увеличением

числа условных уравнений. Последнее необходимо Для увеличения точности

получаемых оценок. В настоящее время обработка результатов совокупных и

совместных измерений осуществляется с помощью электронных цифровых

вычислительных машин, что позволяет использовать для получения оценок

несколько десятков или даже сотен условных уравнений.

Оценку среднеквадратического отклонения результата измерения

величины Y

определяют по формуле

)

( =

(3.43)

где D

— алгебраическое дополнение определителя D, получаемое путем

удаления из него j-й строки и j-го столбца; S

— оценка дисперсии условных

уравнений.

Для определения S

используют формулу

∑ ∑

= =













−

jiji

YkX

(3.44)

Доверительные интервалы для истинных значений всех измеряемых

величин получают на основе распределения Стьюдента при числе степеней

свободы, равном п–т.

Если при совокупных или совместных измерениях условные уравнения

нелинейны, то применяют их линеаризацию [9, 10].

§ 3.7. Результаты и погрешности измерений с однократными

наблюдениями

Технологические измерения с однократными наблюдениями осуще-

ствляются с помощью систем автоматического контроля и имеют наиболее

широкое применение в химико-технологических процессах. Для этих

измерений при проектировании систем автоматического контроля практически

полностью исключены методические погрешности, а личные сведены к

минимуму. Таким образом, всеми погрешностями, кроме инструментальных,

можно пренебречь, поэтому анализ составляющих погрешностей для таких

измерений не проводится.

Прямые измерения. Результат прямого измерения записывают в виде

)(XXA ∆±=

(3.45)

где

— значение физической величины (оценка), найденное по шкале

измерительного прибора:

)(X∆

—абсолютная погрешность для найденного

значения, определяемая классом точности средства измерений.

При оценке значения физической величины по шкале измерительного

прибора необходимо учитывать тот факт, что число делений шкалы

согласовано с классом точности измерительного прибора в соответствии с

формулой (2.4). Поэтому нецелесообразно пытаться на глаз оценить доли

деления и приводить их в результате измерения. Кроме того, при определении

долей деления на глаз операторы допускают систематическую ошибку,

доходящую до 0,2 деления.

По указанным причинам значение измеряемой величины должно быть

считано по шкале с погрешностью в половину деления. При этом необходимо

пользоваться правилами округления:

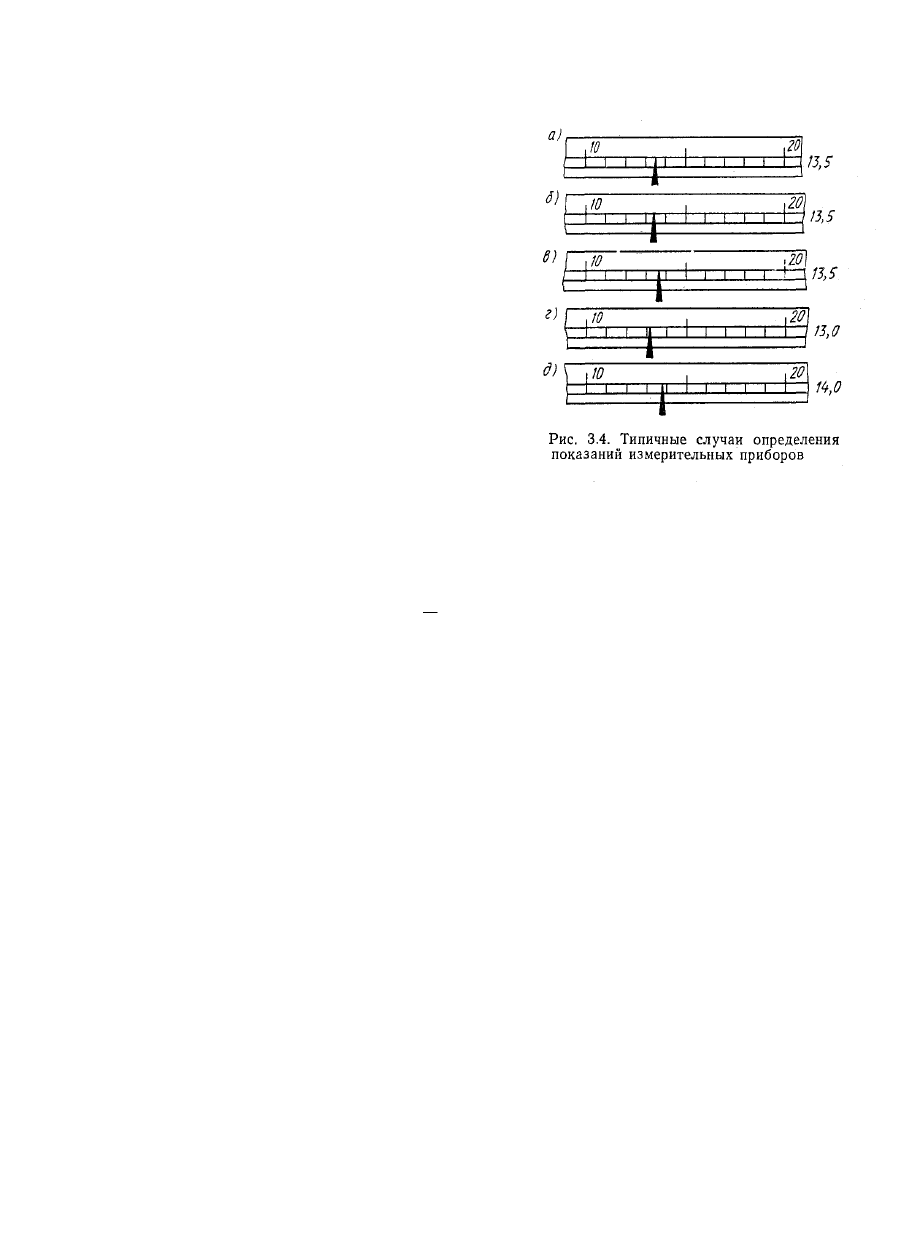
если указатель располагается в

середине деления (рис. 3.4,а), слева (рис. 3.4,

б) или справа (рис. 3.4, в) от нее, то в

значении измеряемой величины указывается

половина деления;

если указатель располагается вблизи

отметки шкалы справа (рис. 3.4, г) или слева

(рис. 3.4, д) от нее, то результат округляется

до значения, соответствующего этой отметке.

Результаты, полученные с помощью

однократных измерений, записывают

выражениями вида (3.45) и в тех случаях,

когда в показания используемого средства

измерений необходимо вносить поправки [см. § 3.3]. В практике технологиче-

ских измерений поправки обычно вносят в показания образцовых средств

измерений. Только после внесения поправок, учитывающих систематическую

погрешность указанных средств измерений и дополнительные погрешности от

влияющих величин, погрешность )(X∆ в выражении (3.45) будет определяться

классом точности образцового средства измерения.

При определении погрешностей измерений, выполняемых с помощью

рабочих средств измерений, обычно вычисляют абсолютную и относительную

погрешности. Первая нужна для определения результата и правильности

записи, вторая — для сравнения его по точности с результатами других

возможных измерений той же физической величины. Расчет абсолютной и

относительной погрешностей осуществляется по паспортным данным средств

измерений в зависимости от формулы, принятой для нормирования его класса

точности.

Если погрешность средств измерений нормируется формулой (2.34), а за

нормирующее значение принят диапазон измерений (например, диапазон

измерений по входу (Х

—X

), то для приведенной погрешности

bXXY

НВ

=−∆= )/(100

(3.46)

здесь b — паспортное значение класса точности средства измерений.

Абсолютная и относительная погрешности для результата измерения

с учетом (3.46) определяются соответственно выражениями:

100/)()(

НВ

XXbX −=∆

(3.47)

XXb

НВ

)(

100

)(

−

∆

=δ

(3.48)

)(Xδ

— относительная погрешность для найденного значения

фи-

зической величины. При Х

=0 выражение (3.48) приобретает вид

XbXX

/)( =δ

(3.49)

Если погрешность средства измерений нормируется формулой (2.33) и в

паспорте его указано значение класса точности, равное с, то абсолютная и

относительная погрешности определяются соответственно выражениями:

100/)( XcX =∆

(3.50)

cX =)(δ

(3.51)

Косвенные измерения. Оценка результата косвенного измерения

определяется на основе оценок аргументов, определяемых путем прямых

измерений с однократными наблюдениями:

),...,,(

21 m

XXXfY =

(3.52)

Результат косвенного измерения записывают в виде

∆

(3.53)

где

∆

— оценка погрешности косвенного измерения.

При определении оценок погрешностей косвенных измерении считают,

что погрешности измерений аргументов являются случайными величинами,

имеющими равномерный закон распределения. На этом основании

предварительно находят абсолютные

∆

) погрешности величин—аргументов

по формуле (3.47) или (3.50), а затем, используя формулу вероятностного

суммирования (3.13), определяют значение указанной оценки [10]:

∑

∆=∆

)(

(3.54)

Относительную погрешность косвенных измерений вычисляют по

формуле [10]:

∑

)(δδ

(3.55)

Предварительно определив относительные погрешности )(

Xδ величин-

аргументов по уравнениям (3.48) или (3.51).

Совокупные и совместные измерения. Оценки результатов и по-

грешностей совокупных и совместных измерений в случае, когда эти измерения

базируются на результатах однократных прямых измерений, могут быть

найдены с помощью зависимостей, приведенных в § 3.6. Эти измерения в

настоящее время еще не нашли широкого применения в автоматическом

контроле технологических параметров. Используют только совокупные

измерения в многопараметрических методах анализа состава

многокомпонентных веществ (см. § 12.2). Обычно для концентраций

определяемых компонентов смеси задача сводится к косвенному измерению

[см. выражение (12.5)]. Поэтому для оценки результатов измерений и

погрешностей могут быть использованы формулы (3.53) — (3.55).

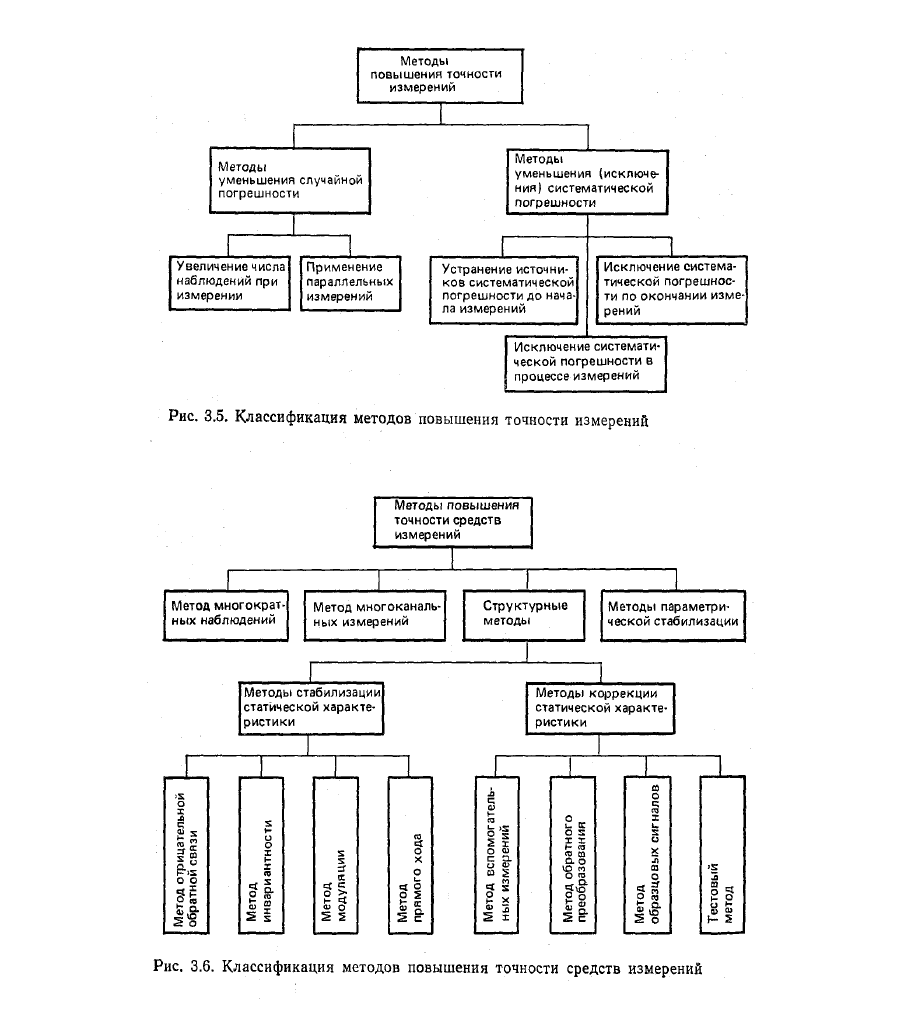
§ 3.8. Методы повышения точности измерений и средств измерений

Повышение точности измерений — актуальная задача практически

любых измерительных экспериментов. Для технологических измерений

повышение точности измерений в настоящее время особенно важно в связи с

переходом к широкому применению АСУ ТП, решающих задачи оптимизации

технологических процессов. Задача повышения точности измерений

неразрывно связана с задачей повышения точности измерительных устройств.

Для решения этих задач применяются различные методы [30, 31],

сущность которых кратко изложена далее. В силу того, что в настоящее время

отсутствуют общепринятая классификация методов повышения точности

измерений и средств измерений, а также общая терминология, в книге

используются классификация и терминология, приведенные на рис. 3.5 и 3.6.

В § 1.4 дан анализ причин возникновения случайной и систематической

составляющих погрешностей измерения. Принципиальное различие в причинах

их возникновения и проявления определяет, специфику методов уменьшения

этих погрешностей.

Методы уменьшения случайной погрешности измерений. Для

уменьшения случайной составляющей погрешности измерений увеличивают

число наблюдений (см. рис. 3.5). Действительно, если следовать зависимости

(3.5), то оценку среднеквадратического отклонения результата измерения,

которая определяет собой случайную погрешность, теоретически можно

сделать как угодно малой, увеличив число наблюдений п. Однако на практике в

большинстве случаев трудно обеспечить постоянство самого объекта

измерений в течение длительного времени, а это может при увеличении числа

наблюдений п привести к увеличению погрешности, а не к ее уменьшению.

Другим методом повышения точности измерений за счет уменьшения

случайной составляющей погрешности (см. рис. 3.5) является