Ежков В.В., Зарудский Г.К., Зуев Э.Н. и др. Электрические системы и сети в примерах и иллюстрациях

Подождите немного. Документ загружается.

-«э -««

-0,333

0,667

-0Д

0,333

(0,333 •H-l)-0,465

0,333

0.15

1-0.446^(0,333.3,75+1)

0Д

0,333

-0,131+0,6

0,607

1,009-0,8697-

ГЛАВА 10

ТЕХНИКО-ЭКОНОМИЧЕСКИЕ РАСЧЕТЫ

ПРИ ПРОЕКТИРОВАНИИ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ

Задача выбора оптимального варианта любого энергетичес-

кого объекта, входящего в состав ЭЭС, в том числе и электричес-

ких сетей различных номинальных напряжений, осуществляющих

распределение ЭЭ по территориям разной площади (местных,

районных, региональных), в соответствии с современной методо-

логией решается на основе сопоставления конкурентоспособных

вариантов по технико-экономическим показателям с использова-

нием критерия минимума приведенных затрат [10.1]. В их состав

в общем случае входят капиталовложения приведенные к од-

ному году нормативного срока окупаемости, издержки на амор-

тизацию, текущий ремонт и обслуживание (И), затраты на ком-

пенсацию потерь мощности и электроэнергии (Зш,т) и вероятный

ущерб от перерывов электроснабжения потребителей (Y). Если

сооружение объекта осуществляется в течение нескольких лет, то

при определении затрат по вариантам учитываются последовате-

льность вложений средств и изменение издержек, а также дина-

мика роста нагрузок сети.

Определению технико-экономических показателей вариантов

предшествует этап выбора технических параметров элементов

сети — сечений проводов ВЛ и кабелей, номинальных мощно-

стей трансформаторов и т. п. Выбор сечений проводов ВЛ осуще-

ствляется на основе экономических критериев с учетом ряда

технических ограничений. При этом широко используются два

метода — экономической плотности тока и экономических

интервалов, иллюстрации применения которых далее уделяется

большое внимание.

Выбор номинального напряжения участков сети тесно связан

с намечаемой конфигурацией ее схемы и условиями обеспечения

надежности электроснабжения узлов нагрузки, в качестве кото-

рых здесь рассматриваются шины 6—10 кВ понижающих подста-

нций с заданными активной и реактивной мощностями. Этим

вопросам посвящен ряд примеров, иллюстрирующих наиболее

характерные ситуации, возникающие в практике проектирования

электрических сетей.

271

в этих примерах использованы технико-экономические пока-

затели, которые представлены в [ЮЛ] и существовали до 1 ян-

варя 1992 г., т. е. до момента либерализации цен в России.

С этого момента они претерпели существенные изменения в сто-

рону увеличения. В условиях прогрессирующей инфляции попыт-

ка их коррекции с помощью введения коэффициентов удорожа-

ния может быть оправданной лишь для конкретного момента

времени, после которого в силу указанных обстоятельств она

неминуемо утратит свою ценность. Вместе с тем если условно

считать, что степень удорожания в среднем для различных видов

оборудования и топлива примерно одинакова, то сопоставитель-

ные расчеты, где в итоге оценивается относительная разница

в затратах по вариантам, могут выполняться и с использованием

старых показателей, приведенных в [10.1]. Поэтому рассматрива-

емые в данной главе задачи при таком подходе сохраняют свою

методическую ценность по крайней мере до того момента, пока

не будет принята новая или скорректирована старая методика

оценки сравнительной экономической эффективности капиталов-

ложений.

Оценка потерь электроэнергии и затрат на их компенсацию.

В любом /-М элементе электрической сети, схема замещения

которого содержит продольные и поперечные ветви с активными

сопротивлениями и про-

водимостями, выделяют-

ся два вида потерь элект-

роэнергии:

— зависящие от на-

грузки элемента ДЭ', т. е.

от протекающего в про-

дольной ветви тока

(«условно-переменные»);

— не зависящие

нагрузки элемента

и определяемые пршю-

женными к поперечным

ветвям напряжениями

(«условно-постоянные»).

Суммарные потери элек-

троэнергии ДЭ,1 склады-

ваются из указанных

двух составляющих:

лэ.х=Аэ:-ьлэ';.

Затраты на компенса-

цию потерь мощности

и электроэнергии в I-M

элементе сети

Зпок

в соот-

ОЭ'

1,0

3.6

5,2

2.В

2,4

2,0

1,6

1,2

1-ОЭС ефопейской части России,

2-031

:Cu<5t4 йь J

~03С

досто ко

Ч.

от

АЭТ

1000 2000 5000 ЧООО 5000^6000 7300 вОООТ,ч/еод

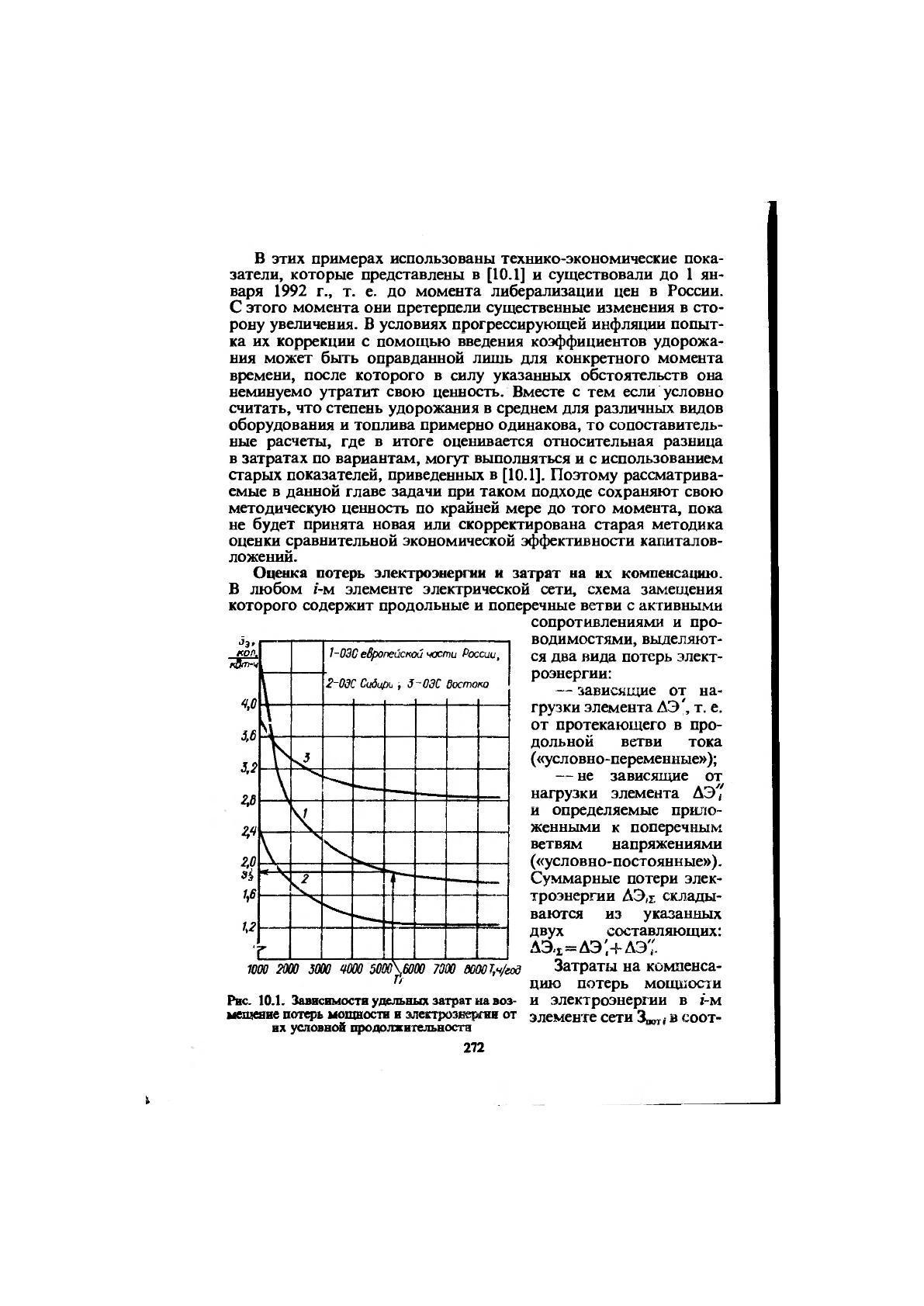
Рис. 10.1. Зависимости удельных затрат на воз-

мииеяие попгфь мощности и злеггрозве^та от

их условной продолжительности

272

ветствии с двумя категориями потерь также имеют две состав-

ляющие: 3„от,=3'ы„г,+Зпот,. Каждая из этих составляющих опреде-

ляется умножением потерь (ЛЭ; или ЛЭ^) на соответствующие

удельные затраты (з'^ или з'^, которые дифференщ1рованы по

трем группам ОЭС (европейской части России, Сибири и Восто-

ка) в виде функций времени Т, характеризующего степень нерав-

номерности конфигурации графика нагрузки элемента сети (рис.

10.1). Удельные затраты на компенсацию нагрузочных потерь

(з'э) определяются по времени 7"= =

Tj/a„,„

а на возмещение

условно-постоянных потерь — времени

Т— Т"—

где т, —

время наибольших потерь мощности; — коэффициент попада-

ния максимума потерь в максимум нагрузки системы; T^i — чи-

сло часов работы /-го элемента за год (время включения) [10.2].

Задача 10.1. Двухцепную линию электропередачи 500 кВ про-

тяженностью 400 км предполагается выполнить проводами

АС500/64 с расщеплением фазы на три провода. Погонное актив-

ное сопротивление фазы линии

Го

0,02

Ом/км, погонное значе-

ние среднегодовых потерь активной мощности на корону

АРжоро

'7,5

кВт/км. Линия должна сооружаться в ОЭС Центра.

График перетока мощности по линии характеризуется числом

часов использования максимальной нагрузки Г„бл=5760 ч/год

и максимальной передаваемой мощностью Pn^x=1800 МВт при

cos ^ =

0,95.

Коэффициент попадания максимума нагрузки линии

в максимум нагрузки энергосистемы к^=0,9.

Определить приведенные затраты на компенсацию потерь

мощности и энергии в проектируемой линии, принимая, что обе

цепи линии включены параллельно в течение года

(Г,жл.л

= 8760

ч/год).

Решение. Предварительно запишем выражение для определе-

ния приведенных затрат на компенсацию потерь мощности и эне-

ргии применительно к рассматриваемому случаю:

3^,л = з;ЛЭл-Ьз:ЛЭл-з;ЛРлш„Тл + з;'АР^Г^л, (10.1)

где

ДЭ л, ЛЭ л

— потери ЭЭ, соответственно зависящие и не

зависящие от нагрузки; з'„'

з э

— удельные затраты на компен-

сацию соответственно ДЭ'л и АЭл; t^ — число часов максималь-

ных потерь моцщости на нагрев проводов (ЛРлтм);

APiop — суммарные среднегодовые потери мощности на корону.

Для вычисления активного сопротивления продольной ветви

П-образяой схемы замещения линин (гд) предварительно найдем

поправочный коэффициент учитывающий распределенность

параметров по длине, ко формуле (1.15):

—х^Ьо^/З. В соот-

ветствии с данными задачи 1.3 погонные реактивные параметры

для рассматриваемой линии составляют Хо=0,3015 Ом/км,

мкСм/ки. Бри этом

ПЪ

А:, = I - 0,3015.3,7

•

I о -

400^/3=0,9405

Гл

Го

Ikrln^=0,02.400

•

0,9405/2=

3,762

Ом.

Определяем максимальные потери мощности на нагрев про-

водов линии

выражению

АРлш« = [^'ш.х/(С/»«С08ф)]2гл (10.2)

в соответствии с (10.2)

АРлп»х=[1800/(500

• 0,95)]2 •

3,762=(3,789)^

•

3,762 «

МВт.

Определяем суммарные среднегодовью потери мощности на

корону:

АР«р=ИцАР.сро/=2-7,5.10-^400=6 МВт.

Таким образом, суммарные потери активной мощности в ре-

жиме наибольшего перетока

АРЛ1=АРлп«+АР„р=54+6=60 МВТ,

или в процентах от передаваемой мощности

ДРлг=(^Рл^/Рщ») •

100=(60/1800). 100=3,33%.

Число часов максимальных потерь мощности на нагрев про-

водов линии приближенно

т=(0,124+ Т^

•

10" Y

• 8760.

(10.3)

В соответствии с (10.3) для рассматриваемой линии

тл=(0,124+

5760 •

10-^)2.8760 =4290 ч/год.

Определяем годовые потери энергии в линии:

АЭл = АРлп«Тл=54.10'-4290 =231,66.10® кВт ч/год,

ЛЭл=АР.ор7'»слл=6-10'-8760=

52,56.10®

кВт ч/год,

АЭЛ1=АЭЛ+АЭЛ=(231,66 +

52,56).

10®=284,22.10® кВт ч/год.

Передаваемая по линии за год энергия

Эл=Рп« 1800.10'.5760 = 10368.10® кВт.ч/год.

Относительное значение годовых потерь электроэнергии (в

процентах от Эд)

А^х=(АЭлг/Эл). 100=(284Д2/10368). 100 «2.74%.

274

Определяем коэффициент попадания максимума потерь мощ-

ности на нагрев проводов линии в максимум нагрузки системы

и значение

Т'я

= Тл/а«=4290/0,81«

5300

ч/год.

Определяем значения удельных затрат на компенсашио по-

терь по кривой 1 рис. 10.1, соответствующей ОЭС европейской

части России:

— для ^=5300 ч /год получаем 3, = 1,9 коп/(кВт

•

ч),

— для Гл = 7'^л=8760 ч/год получаем з';= 1,75 коп/(кВт

•

ч).

По выражению (10.1) определяем полные затраты на компен-

сацию потерь мощности и электроэнергии:

3^.л=

1,9 •

10"" -231,66.10®+1,75.10"®

•

52,56

•

10®«

«4,4+ 0,92=

5,32

млн. руб/год.

Определяем доли затрат на компенсацию потерь на нагрев

проводов и на корону:

^^тл=(3'„отл/3„отл)-100=(4,4/5,32).

100

= 82,7%,

100=(0,92/5,32). 100= 17,3%.

Полученные результаты свидетельствуют о том, что затраты

на компенсацию потерь, зависящих от нагрузки, примерно в пять

раз превьш1ают затраты на компенсацию потерь на корону.

Задача 10J2. На понижающей подстанции установлены два

двухобмоточных трансформатора типа ТДН-16000/110 со следу-

ющими параметрами:ЛР,=85 кВт, АР,=

кВт. В течение време-

ни A/j=2000 ч/год нагрузка подстанции на ншнах 10 кВ мак-

симальна: Р^=20 МВт. В течение времени А/2= 8760—А/^ нагруз-

ка подсташщи минимальна/

P2=e^Pi (рис. 10.2). На^

грузка характеризуется ко-

э^ициентом мощности

cos ^=0,9, который при-

нимают неизменным

в течение года. Подстан-

Щ1Я

сооружена в ОЭС Во-

стока.

Определить потери эле-

ктроэнергии в трансформа-

торах подстанции за год

для двух случаев:

-^6760

t,4

ЛЬ

Рк. 10.2 Условный двухлупевчатый •ра-

фик агтной вагрузжн подстанщш

275

А — параллельная работа трансформаторов в течение всего

года;

Б — отключение одного из трансформаторов в режиме мини-

мальной нагрузки.

Выяснить, при каких значениях а, экономически целесообраз-

но отключение одного из трансформаторов при минимальной

нагрузке (случай Б).

При решении задачи принять, что коэффициент попадания

максимума нагрузки подстанции в максимум нагрузки энергоси-

стемы 1, а значение а, меняется в диапазоне 0,3 — 0,6.

Решение. Потери электроэнергии в трансформаторах скла-

дываются из потерь в обмотках («в меди»), зависящих от нагруз-

ки (ЛЭт). и потерь в магнитопроводе («в стали»), принимаемых

условно-постоянными (ЛЭт):

ЛЭт£=АЭ'Т+АЭ';.

Рассмотрим случай А, когда оба трансформатора включены

параллельно в течение всего года. Потери ЭЭ на нагрев обмоток

на каждой (i-й) ступени графика нагрузки определяем по извест-

ному выражению

J /i^/cos q)\2

ДЭ'т,=АР. А/„ (10.4)

«Ti \ JTiioM /

где

АРм<

— потери в меди при нагрузке пп — число парал-

лельно работающих трансформаторов; STBOM — номинальная мо-

щность трансформатора.

Тогда годовые потери электроэнергии на нагрев обмоток

в случае А составят

АЭ'Т(Л)=АР„,(а)А/1 +

АР«2(А)А/2.

(10.5)

С учетом (10.4) и того, что P2=ex,Pi, из (10.5) получим

=^ДрУ^^У[Д^+а^(8760-Д/,)]. (10.5а)

2 \ /

Вьфажение перед квадратной скобкой представляет собой

потери мощности на нагрев обмоток в режиме наибольшей на-

грузки подстанции, т. е. АРт,б- Следовательно, выражение в квад-

ратных скобках есть не что иное, как время наибольших потерь

мощности:

276

Т,Л)=ЛЭ'Т(А)/АР'ТЯ6 = (1 8760а^. (10.6)

Годовые потери ЭЭ в стали двух трансформаторов

в случае А:

ДЭ'Т{А)

ИТДЛ7'.ЖЛ(А)

2. 19

.8760=332,88 тыс. кВт

ч/год.

Теперь рассмотрим случай Б, когда в течение времени Л^^

работают два трансформатора, а в течение времени A/j — один.

В соответствии с выражением (10.5), где индекс А заменен на Б,

имеем

^ \ '^ИОМ / \ J

= ДР'т^ [A/i + 2

(8760

-At у}]. (10.56)

При этом

Т(Е,

= АЭ'т(н)/АР'т„б=(1 -

а J)+8760.2 а (10.6а)

Потери электроэнергии в стали трансформаторов в слу-

чае Б:

АЭ

т(Б)=2 ЛР,

ЛГ1

+ АР, At2=2

АР, [Аг^

+0,5 (8760 -

А/^)].

(10.7)

В (10.7) выражение в квадратных скобках представляет собой

эквивалентное время включения двух трансформаторов в режиме

использования Б:

Т'.иСБ)=0,5

Ati+4380 =

5380

ч/год.

При этом

АЭ ^(Е)=2 АР,

Г^(В)=2 19.5380 =

204,44

тыс. кВт

•

ч/год.

Потери мощности в обмотках трансформаторов при наиболь-

шей нагрузке

АР'т^=АР„,=1.85

/20/09^4

«82 кВт,

а при наименьшей нагрузке

AP^=alAPj^=S2aj. (10.8)

Удельные затраты на компенсацию потерь (з,, з,) определяем

по кривой 3 рис. 10.1, соответствующей ОЭС Востока, по зна-

чениям Т(А.ч и ^^(AJB). Значение з^'(А) при 7',М(А)=8760 ч/год

равно 2,85 коп/(кВт-ч), а з^да при 7'„(Б)=5380 Ч/ГОД —2,9

копДкВт

•

ч).

277

Суммарные затраты на компенсацию потерь вычисляем по

выражению

ЗоотТ(А,Б) = 3 АРТ„6Т(А.Б) + ЗЭ(а.Б)2АР» 7Wa(A.E) =

= 3',(А,Б) АЭ Т(А.Б) + 3 VB)

АЭ ^(А,Б)-

(10.9)

Результаты определения составляющих потерь электроэнер-

гии и затрат на их компенсацию приведены в табл. 10.1, где

^IOTT — [(ЗпотТ(А) — ЗпотТ(К))/31ютТ(А)] ЮО-

Таблица 10.1. Результаты расчета потерь электроэнергия

• затрат ва ах комоевсацию

(10.10)

Ва-

рв-

аят

г,

ч1тоа

жоп/

(кВтч)

дэ;.

тыс.

жВт.<

год

лэ;

тыс.

KBT-V

год

ДЭ„.

ТИС.

жВтч/

год

руб/год

З..Г

руб/год

ЗпотТ.

руб/год

ДЗоотТ.

0.3

А 2608 3,15

213.85 332,88 546.73

6736.3

9487,1

16223,4

+ 13,4

0.3

3217

3.08

263,74 204,44 468,18

8123,2 5928,8

14052,0

+ 13,4

0.4

А 3082 3.09

252,67 332,88 585,55 7807,5

9487,1 17294,6

+ 6,7 0.4

4163 2,99

341,30 204,44

545,74

10204,9 5928,8

16133,7

+ 6,7

0.5

3690 3,03

302,58 332,88

635,46

9168,2

9487,1 18655,3

-0,3 0.5

Б 5380 2,90 441.05

204,44

645,49 12790.5 5928,8

18719,3

-0,3

0.6

А 4434 2,96

363,48 332,88 696.36 10759.0 9487,1 20246,1

-8.8 0.6

Б 6867 2,86

562,99 204,44 767.43 16101,5

5928,8 22030,3

-8.8

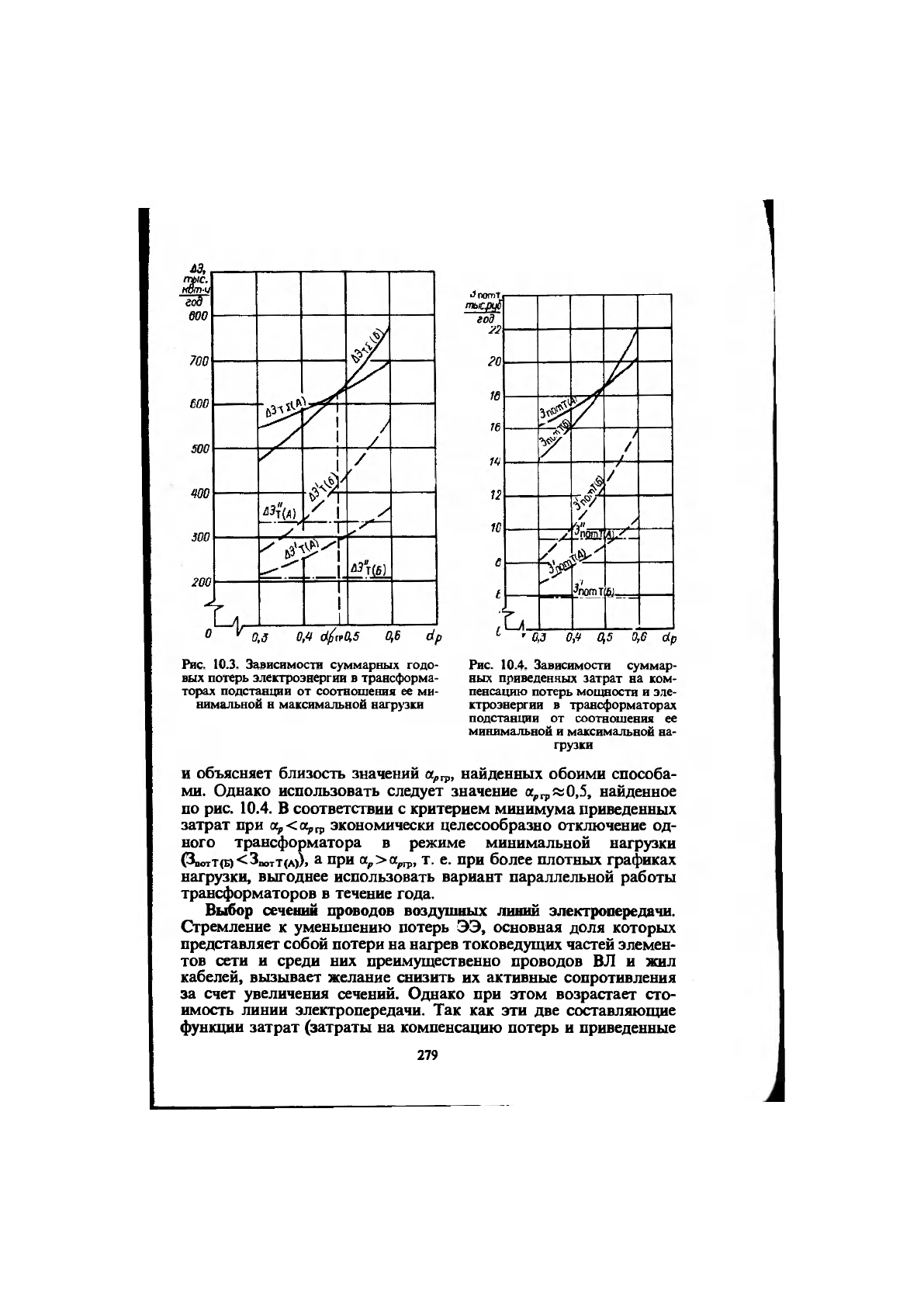
На рис. 10.3 показаны зависимости суммарных потерь ЭЭ

и их составляющих от соотношения минимальной и максималь-

ной нагрузок (Up). Их анализ показывает, что при параллельной

работе двух трансформаторов в течение года (слз^чай А) нагру-

зочные потери меньше, чем в случае Б (ЛЭ^(А)<

АЭ'т®)-

Обратное

соотношение характерюует потери ЭЭ в стали трансформаторов

(АЭТ{А)>АЭТ(Б))- ЭТИ обстоятельства имеют следствием то, что

зависимости суммарных потерь ЭЭ имеют точку пересечения при

значении При а,<о^гр АЭт1(б)<ДЭп:(а). и наоборот.

Аналогичный характер имеют зависимости суммарных затрат

на компенсацию потерь и их составляющих, показанные на рис.

10.4. Вместе с тем значение о^гр, соответствующее точке пересече-

ния зависимостей 3O„T(A) И 3„„ТТ(Б) ОТ несколько отличается от

определенного по рис. 10.3, что объясняется различием значений

удельных затрат з, и з j для случаев А и Б. В рассматриваемом

частном случае графика нагрузки подстанции (А/^=2000 ч/год)

это различие оказывается незначительным (см. табл. 10.1), что

278

еод

О,и о(/гРй5 0,6 dp

^nomTi

Рис. 10.3. Зависимости суммарных годо-

вых потерь электроэнергии в трансформа-

торах подстанции от соотношения ее ми-

нимальной н максимальной нагрузки

Рис. 10.4. Зависимости суммар-

ных приведенных затрат на ком-

пенсацию потерь мощности и эле-

ктроэнергии в трансформаторах

подстанции от соотношения ее

минимальной и максимальной на-

грузки

объясняет близость значений ар^, найденных обоими способа-

ми. Однако использовать следует значение а^^аО.З, найденное

по рис. 10.4. В соответствии с критерием минимума приведенных

затрат при ар<аргр экономически целесообразно отключение од-

ного трансформатора в режиме минимальной нагрузки

(ЗПОТТ(Б)<ЗПОТТ(А)).

при OLPXIP^, Т. е. при болве плотных графиках

нагрузки, выгоднее использовать вариант параллельной работы

трансформаторов в течение года.

Выбор сечений проводов воздушных линий электропередачи.

Стремление к уменьшению потерь ЭЭ, основная доля которых

представляет собой потери на нагрев токоведущих частей элемен-

тов сети и среди них преимущественно проводов ВЛ и жил

кабелей, вызывает желание снизить их активные сопротивления

за счет увеличения сечений. Однако при этом возрастает сто-

имость линии электропередачи. Так как эти две составляющие

функш1и затрат (затраты на компенсацию потерь и приведенные

279