Ежков В.В., Зарудский Г.К., Зуев Э.Н. и др. Электрические системы и сети в примерах и иллюстрациях

Подождите немного. Документ загружается.

ния коэффициентов z\

(0,3 —Л/)

и (0,4—Л/) соответственно. Выбе-

рем в качестве столбца s первый (переменная дс^ вводится в ба-

зис). Определим переменную, выходящую из базиса, по наимень-

шему значению <x,=bilai,. Очевидно, что ю базиса должна выво-

диться переменная х^. В столбце указаны значения

коэффициентов пересчета. Пересчет всех элементов таблицы для

всех строк, кроме той, что соответствует переменной, уходящей

из базиса, выполняется по формуле

для (8.5)

Для строки q все значения коэффициентов определяются

делением на коэффициент щ,. Покажем пересчет. Так как первая

строка соответствует переменной х-^, уходящей из базиса, то все

значения коэффициентов делим на 1, т. е. остаются прежни-

ми. Заметим, что вторая строка также остается неизменной,

поскольку входящая в базис переменная jc^ отсутствует в данной

строке: а^^—О. Пересчет третьей строки:

г,у)=700-1

-400

300,

fliV= 1-11=0,

аУ^=1_1.0 =

аУ^=0-Ы = -1, 0^=0-10=0,

а^У=-1_1.0=-1, 0^=1-1.0=1.

Пересчет целевой строки:

-10-700 А/-(0,3-Л/)400= -130 -

300

Л/,

с1')=0,3-Л/-(0,3-Л/)1 =

с^ч=0.4-Л/-(0,3-Л/)0=0,4-Л/,

су)=0-(0,3-Л/)1=Л/-1, сУ)=0-(0,3-Л/)0=0,

с^'>=Л/-(0,3-Л/)0=Л/, с^ч=0-(0,3-Л/)0=0.

В табл. 8.2 приведены пересчитанные значения элементов

табл. 8.1.

Таблица 8.2. Первая втерацая

*6аз

«5

Щ А-

0,3

400

300

-1

400

300

. 0

—

-130-

-300 А/

0 0.4-

-М

м-

-0.3

0 м 0 0,4-А/

Из табл. 8.2 видно, что в число базисных нужно ввести

переменную Х2, так как коэффициент при ней в целевой строке

отрицателен. Из числа базисных выводится переменная х^.

В табл. 8.3 приведены пересчитанные значения элементов табл.

220

8.2. Поскольку в табл. 8.3 отсут-

ствуют отрицательные коэффици-

"Г".

енты в целевой строке, то реше- _

ние оптимально:

= Pj=400 МВт,

Х2

= Р2 =

300

МВт,

Х4=!00МВТ,

при ЭТОМ И = 250. Как видно из Схема энергосистемы

выражений для И^ (Р^) и ИгСРг)» при одном и том же значении

Р всегда M2>Hj, т. е. вторая тепловая электростанция менее

экономична, чем первая. Поэтому в полученном оптимальном

решении первая электростанция загружена полностью, а вторая

недогружена на 100 МВт, о чем свидетельствует ненулевое значе-

ние Х4.

Таблица 8.3. Оппмальвое решете

0,3 400 1

0 0

0 100 0

1 1 1 -1

0.4

300 0

1 -1

-1 1

—

— Z

-250 0 0 0,1

0 0.4 А/-0.4

Задача 8.2. Пренебрегая потерями активной мощности в сетях,

найти оптимальную нагрузку электростанций для энергосисте-

мы, представленной на рис. 8.1. Распределению подлежит актив-

ная нагрузка, равная Ря=:180 МВт, Характеристики удельных

приростов КЭС таковы:

= 3+0,2Pi + 0,004Pf;

62=4+0,15^2+0,003 Р|;

ЕЗ=2-Н0,4РЗ-Ю,002Р|.

Решение. Математическая формулировка задачи имеет сле-

дуюпшй вид [8.5, 8.7]:

найти

(8.6)

при условии

min M(Pi. Р2. Р3)

(8.7)

Так как в качестве целевой функции используются затраты на

топливо на электростанциях энергосистемы И=И1-|-И2-нИз,

а производные от расходных характеристик — характеристики

dHi(Pd

удельных приростов Е<= , согласно условиям задачи, нели-

dP,

221

нейны, то задача относится к задачам на поиск экстремума

с ограничениями-равенствами при нелинейной целевой функции.

В задаче имеется одно ограничение — условие баланса активной

мощности в энергосистеме. Переменными являются активные

мощности станций, т. е. Р^. Р^ и Р3. Число переменных больше

числа ограничений, и, следовательно, оптимизация возможна.

Применим для поиска решений градиентный метод [8.1, 8.3, 8.5,

8.7].

Разобъем искомые переменные на два вектора. В качестве

вектора нюависимых переменных Y выберем все мощности стан-

ций, за исключением балансирующей. Примем в качестве балан-

сирующей конденсационную электростанцию КЭС

Тогда

В качестве вектора зависимых переменных X выступает пере-

менная Р^:

Необходимое условие минимума целевой функции — равен-

ство нулю производных от И по всем независимым переменным

у„ т. е. компонент g, градиента И;

gi-

дщг. лг)^^ аи(г. X)

ду1 , дх, dyi

(8.8)

Так как

аи йи . , „ ги аи,

—=—=£,. 1=1,2; —=—

ду! dPi дХ дР^ '

81V dW ^ dW SW ,

—=—=1; —=—=1, 1=1,2,

дХ ЪР^ ду, dPi

ТО

окончательно получаем

Я,=«/-£3 =

/=1.2. (8.9)

Для поиска решения применим метод последовательных при-

ближений. Зададим исходное приближение вектора У: Pf'=60

МВт, Pf = 70 МВт.

Вычисляем мощность третьей станции из уравнения баланса:

Р^=Р,_Р\0)_Р5»= 180- 60- 70= 50 МВт.

Вычисляем градиент в начальной точке по (8.9):

При выбранном исходном приближении Р^°^=60 МВт,

Р^о)=70 МВт и найденном значении мощности балансирующей

станции Р$''=50 МВт находим:

222

е f=3 +

•

60 + 0,004.60^=29,4 рубДМВт

ч);

ef=4+0,15.70+0,003.70^=29,2 руб/(МВт

•

ч);

ef =2 + 0,4.50+

0,002- 50^

27,0

рубДМВт ч).

Составляющие градиента в исходной точке:

-63=29,4-27=2,4;

g5«=E2-E3 = 29 -

Модуль градиента в исходной точке

Оценим точность расчета по модулю градиента. Расчет закон-

чен, если |g(t)|<0,15.

Выбираем пробный шаг Тогда

р =Pf>-h <°)g f=60 - 0,7

• 2,4

58,32

МВт,

py)=pf-0,7.2=68,6 МВт.

Вычисляем мощность балансирующей станции:

= 180 - 58,32 - 68,6 =

53,08

МВт.

Значения удельных приростов и компонент вектора-градиента

в новой точке:

Б =3+0,2

• 58,32

+0,004

•

58,32^=28,269;

=4+од 5.68,6+0,003

•

68,6^=28,408;

Б у)=2 + 0,4.53,08 +

0,002 •

53,08^=28,867;

gV>=28,269-28,867= -0,598;

gi'>=28,408 - 28,867= -0,461.

Модуль градиента в этой точке

1^У^1

= ч/(-0.598)^ + (-0,461Я=0,755.

Найдем скалярное произведение g'"* и g^^^ и определим его

знак, чтобы выяснить, больше или меньше оптимального вы-

бранный нами шаг

^(0)^0)^2,4 (-0,598) +

2 (0,461)

< 0,

т. е. выбранный шаг больше оптимального. Принимаем

<'>=0,7.0,4=0,28.

Вычисляем новые мощности станций. Дальнейшие результа-

ты расчета представлены в табл. 8.4.

223

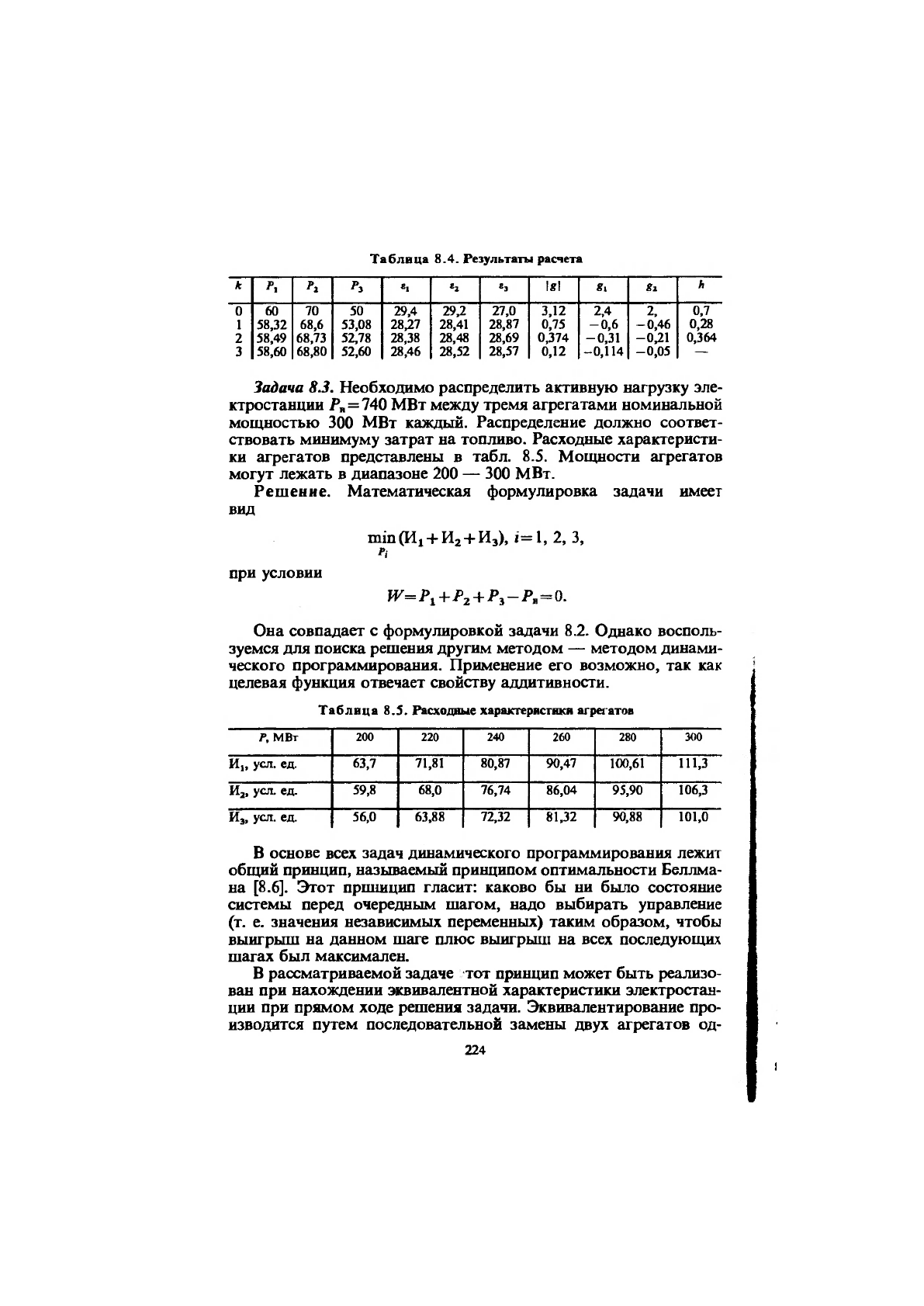
Таблица 8.4. Результаты расчета

А:

«1 «1

«3

1«1

0 60

70 50

29,4

29Д 27,0 3,12 2.4

0,7

58,32

68,6 53,08 28Д7 28,41

28,87

0,75 -0,6

-0,46 0,28

58,49 68,73 52,78

28,38 28,48 28,69 0,374

-0,31

-0Д1

0,364

58,60

68,80 52,60 28,46 28,52 28,57 0,12 -0,114 -0,05

—

Задача

8.3. Необходимо распределить активную нагрузку эле-

ктростанции Р„=140 МВт между тремя агрегатами номинальной

мощностью 300 МВт каждый. Распределение должно соответ-

ствовать минимуму затрат на топливо. Расходные характеристи-

ки агрегатов представлены в табл. 8.5. Мощности агрегатов

могут лежать в диапазоне 200 — 300 МВт.

Решение. Математическая формулировка задачи имеет

вид

при условии

ттСИх-ьИг-ьИз), 1=1, 2, 3,

Она совпадает с формулировкой задачи 8.2. Однако восполь-

зуемся для поиска решения другим методом — методом динами-

ческого программирования. Применение его возможно, так как

целевая функция отвечает свойству аддитивности.

Таблица 8.S. Расходные харакгерястшся агрегатов

Р, МВт

200

220

240 260 280 300

И„ усл. ед.

63,7 71,81 80,87

90,47

100,61 111,3

Иц усл. ед.

59,8 68,0 76,74

86,04

95,90 106,3

И„ усл. ед.

56,0

63.88 72,32 81.32

90,88 101,0

В основе всех задач динамического программирования лежит

общий принцип, называемый принципом оптимальности Бвллма-

на [8.6]. Этот пршшцип гласит: каково бы ни было состояние

системы перед очередным шагом, надо выбирать управление

(т. е. значения независимых переменных) таким образом, чтобы

выигрыш на данном шаге плюс выигрыш на всех последующих

шагах был максимален.

В рассматриваемой задаче тот принцип может быть реализо-

ван при нахождении эквивалентной характеристики электростан-

ции при прямом ходе решения задачи. Эквивалентирование про-

изводится путем последовательной замены двух агрегатов од-

224

ним эквивалентным. На каждом шаге присоединяется только

один агрегат к уже наЁденному эквивалентному. Так, эквивалент-

ная расходная характеристика агрегата, эквивалентного агрега-

там 1 к 2, определяется выражением

H?>(P<^))=min {И,

(Р^)}

(8.10)

=min {Иг (Рг^ + Hi (Р® - Рг)}-

С помощью этого выражения, принимая некоторое значение

суммарной нагрузки двух агрегатов Р® и варьируя Р^, можно

легко найти то значение Pj, при котором издержки на расход

топлива эквивалентным агрегатом И?' будут минималь-

ными. Расходная характеристика всей станции, имеющей три

агрегата,

И « =min {Из (Рз)+И « (Р -

Рз)}.

(8.11)

при обратном ходе по суммарной нагрузке электростанции

находят мощности отдельных агрегатов. Приступим к решению

задачи.

Из табл. 8.5 видно, что самым экономичным является третий

агрегат. Он имеет самые низкие значения эксплуатационных

расходов при всех значениях мощности. Поэтому будем считать,

что при нагрузке станции, составляющей 200 300 МВт, за-

гружается только третий агрегат. Построение эквивалентной

характеристики станции начнем именно с этого агрегата. При

двух включенных агрегатах станция может нести нагрузку в диа-

пазоне 400 — 600 МВт и не может иметь нагрузку, лежащую

в интфвале от 300 до 400 МВт. При работе трех агрегатов

допустимый диапазон изменения их мощности равен 600 — 900

МВт. В этом случае станция не может нести нагрузку

— 200

и 300 — 400 МВт.

Начнем построение характеристики при двух включенных аг-

регатах. Считаем, что в этом случае будут включены более

экономичные агрегаты — третий и второй.

При нагрузке станции 400 МВт вариантов нет — оба агрегата

должны работать с минимальной нагрузкой 200 МВт:

И®=И2 (200)+Из (200)=59,8 + 56,0= 115,8,

При нагрузке 420 МВт уже имеется выбор. В табл. 8,6

приведены варианты загрузки агрегатов при нагрузке станции

420 МВт.

225

7-263

Таблица 8.6. Варяаты загрузки агрегатов

пра вагрузке сташош 420 МВт

Pj, МВт

200 220

Я,, МВт

220 200

И, (Я.)

59,8 68,0

63,88

56,0

и «(Я®) 123,68

124,0

Очевидно, что при данной нагрузке стащщи наилучшим явля-

ется вариант ^2=200 МВт и Рз=220 МВт. При этом расход на

топливо И,(Ра)=

123,68.

Именно эта точка должна войти в эк-

вивалентную расходную характеристику станции. Рассмотрим

варианты при мощности станции 500 МВт (табл. 8.7).

Таблица 8.7. Варяаигы загрузка агрегатов пра вагрузке станции 500 МВт

Рг, МВт

200

220

240

260

280

300

/>„ МВт

300

280

260

240

220

200

И,

59.8

68,0

76.74

86,04

95.9

106,3

И,

101,0

90,88

81,32

72,32

63,88

56,0

И®

160,8

158,88

158,06

158,36

159,78

162,3

МВт

240

Как видно из таблицы, при условии, что нагрузка станции

составляет 500 МВт, наилучшим является решение, при котором

Р2=240 МВТ и РЗ=260 МВт. Суммарный расход при этом

наименьший из всех возможных и составляет 158,06. Аналогично

рассчитывают варианты при других значениях нагрузки станции,

покрываемой двумя агрегата\ш. В табл. 8.8 приведена эквива-

лентная характеристика двух агрегатов, включаюшая наилучшие

решения при каждом значении нагрузки.

Таблица 8.8. Эквввалеятнаа характерастшса двух агрегатов

МВт 400 420

440

460 480

500

520 540 560

580 600

и«

115,8

123,68

132,12 140,32 149,06

158,06

167,36

176,92

186,78 196,9 207,3

Р1', МВт

200 200 200 220 240

240 260 260 280

280 300

Аналогично ведут расчет на третьем шаге, когда рассматрива-

ют работу трех агрегатов. В этом случае при построении эк-

вивалентной расходной характеристики трех ахрегатов использу-

ют расходную характеристику последнего невключенного агрега-

та (первый) и эквивалентную расходную характеристику двух уже

работающих агрегатов, приведенную в табл. 8.8. Мощность стан-

ции при трех работающих агрегатах изменяется от 600 до 900

226

МВт. При шаге изменения мощности 20 МВт надо рассчитать 16

точек характеристики. Покажем расчет некоторых из них.

Рассмотрим работу станции с нагрузкой 600 МВт. Очевидно,

что в этом случае все три агрегата работают с минимальной

нагрузкой и расход на топливо составляет 179,5. Однако имеется

еще один вариант обеспечения нагрузки станции 600 МВт. Если

нагрузка третьего агрегата равна нулю, то два оставшихся аг-

регата могут взять нагрузку 300 МВт каждый. При этом суммар-

ный расход составит 207,3. Очевидно, что из двух рассмотренных

вариантов первый экономичнее. Он и включен в эквивалентную

характеристику электростанции.

При нагрузке электростанции 900 МВт выбор отсутствует: все

три агрегата должны работать с максимальной нагрузкой. При

этом суммарный расход на топливо составит 318,6. При других

значениях мощности электростанции имеется выбор из несколь-

ких вариантов. Рассмотрим нагрузку станции 740 МВт. Возмож-

ные варианты обеспечения этой нагрузки представлены в табл.

8.9. Здесь же приведены варианты и для некоторых других значе-

ний мощности станции (наилучшие варианты для каждого из

рассмотренных режимов станции подчеркнуты). В табл. 8.10

приведена эквивалентная расходная характеристика электростан-

ции. В ней указаны нагрузка станции, суммарный расход на

топливо, а также условно-оптимальная нагрузка первого агрега-

та. С ее помощью можно путем выполнения обратного хода

динамического программирования определить оптимальную за-

грузку агрегатов при любой нагрузке станции.

Таблица 8.9. Варшшты 3aii>y3Kii трех aiperaroB

рт

И,

ИР)

'Г

740

200

220

240

540

520

500

63,7

71,81

80,87

176,92

167,36

158,06

240,62

239,17

238,93

240

260

280

300

480

460

440

90,47

100,61

111,3

149,06

140.32

132,12

239,53

240,93

243,42

760

200

220

240

560

540

520

63,7

71,81

80,87

186,78

176,92

167,36

250,48

248,73

248ДЗ

240

260

280

300

500

480

460

90,47

100,61

111,3

158,06

149,06

140,32

248,53

249,67

251,62

... ... ... ... ...

... ...

840

240

260

600

580

80,87

90,47

207,3

196,9

288,17

287,37 260

280

300

560

540

100,61

111,3

186,78

176,92

287,39

288^2

...

227

Таблица 8.10. Эквшвалсятваа харакгерктшса трех агрегатов

МВт

600

620

640

660 680

700

720

740

Mf^ усл. ед.

179,5 187,38

195,49

203,93 212,13 220,87

229,87 238,93

МВт

200

220

220 220 220

220 240

МВт

760 780

800

820

840 860

880

900

И®, усл. ед.

248^3

257,79 267,39 277,25 287,37 297,51 307,91

318,6

Р1\ МВт

240 240

260

260 260

280

300

В условии задачи было предложено распределить между аг-

регатами нагрузку 740 МВт. Эта операция осуществляется при

выполнении обратного хода динамического программирования.

Покажем, как это делается.

В табл. 8.10 ищем значение мощности первого агрегата при

нагрузке станции МВт. Определяем, что Р^=240 МВт.

Это уже не условно-оптимальное значение, а оптимальное при

заданной нагрузке станции. Определяем нагрузку, приходящуюся

на два оставщихся агрегата: =740 -

240

500

МВт.

По этому значению мощности в табл. 8.8 определяем оптималь-

ную нагрузку второго агрегата Р2=240 МВт. Теперь мощность

третьего агрегата определяем простым вычитанием:

Рз=рР)_Р2 = 500 -

240

= 260 МВт. Задача решена.

Задача 8.4.

Для энергосистемы сравнительно небольшой мощ-

ности требуется определить оптимальное увеличение генериру-

ющей мощности на ближайшие пять лет. Необходимые по про-

гнозу значения суммарной генерирующей мощности энергосисте-

мы на каждый год пятилетнего периода приведены в табл. 8.11.

В исходный момент эта мощность составляет 750 МВт. Ее можно

увеличить вводом агрегатов мощностью 100 либо 150 МВт,

причем в год может бьггь введено не более двух агрегатов

суммарной мощностью не более 250 МВт. Принять удельные

капиталовложения равными Куд=350 руб/кВт. Для определения

приведенных затрат использовать выражение

Z= i (^К,+ЛИ,)(1 + (8.12)

где £1^=0,12 1/год; к,=куд(100п1+150п2) руб; Пу и п^ — целые

числа; АИ,=:И/—руб/год; До 0,08. Ежегодные издержки

ЛИ, принять равными 9,4%.

Таблица

8.11.

Пропюзарусмые

шсобхолмой

пткшоуешЛ

мощ

«.год

0 1

3 4 5

Р^,

МВт

750 826 859

894 929

966

228

Решение. Приведем математическую формулировку задачи.

Итак, необходимо найти значения ежегодного приращения гене-

рирующей мощности А/*!. ДР2.

—.

Д-Ps такие, чтобы для каждого

года выполнялись ограничения

ЛР«=100П1 +

150П2;

(8.13)

«1

= 0,1,2; «2=0.1

и целевая функция (8.12) имела минимальное значение.

Поскольку целевая функция является аддитивной, то для ре-

шения задачи можно воспользоваться методом динамического

программирования. Применительно к рассматриваемой задаче

в соответствии с принципом оптимальности может быть записа-

но соотнощение

Z«=min{3,(AP,)+Z"-«}. (8.14)

Здесь АР, — приращение генерирующей мощности в год / рас-

сматриваемого периода (/=1, ..., 5); 3,(ДР,) — затраты на ввод

мощности в год /:

3,(AP,)=(i5;

АИ,)(1

+£„)'-'; (8.15)

— значение целевой функции на предыдущем шаге при

суммарном приращении мощности за весь предыдущий период;

AP£-«=APi + ...+AP,_,.

В исходный момент суммарная генерируемая мощность си-

стемы составляет 750 МВт (см. табл. 8.11). В первый год рассмат-

риваемого периода это значение должно быть не меньше 826

МВт. Следовательно, в первый год должен бьпъ введен агрегат

100 МВт. Но, может быть, в этом году целесообразно ввести

большую мощность. Найдем приведенные затраты на ввод раз-

личной мощности в этот год. При этом должны быть выполнены

ограничения

P<'>=750+APj>826 МВт,

APj

= 100 +150 < 250 МВт.

Приведенные затраты определяем следующим образом:

при f=l

(АР,)=(£, JSTi+И0(1

=0,12

J^i

0,094

ЛГ^=0Д14Л:,.

В первый год можно ввести либо один агрегат мощностью

100 МВт, либо один агрегат мощностью ISO МВт, либо два

229