Everitt B.S. The Cambridge Dictionary of Statistics

Подождите немного. Документ загружается.

Nested case-control study: A commonly used design in

epidemiology

in which a cohort is

followed to identify cases of some disease of interest and the controls are selected for each

case from those at risk when a subject becomes a case for comparison of exposures. See also

retrospective design, nested case-control study and case-cohort study.[Statistics in

Medicine, 1993, 12, 1733–46.]

Nested design: A design in which levels of one or more factors are subsampled within one or more

other factors so that, for example, each level of a factor B occurs at only one level of another

factor A. Factor B is said to be nested within factor A. An example might be where interest

centres on assessing the effect of hospital and doctor on a response variable, patient

satisfaction. The doctors can only practice at one hospital so they are nested within hospitals.

See also multilevel model.

Nestedmodel: Synonym for hierarchical model and multilevel model .

Network: A linked set of computer systems, capable of sharing computer power and/or storage

facilities.

Network sampling: A

sampling design

in which a simple random sample or stratiﬁed sample of

sampling units

is made and all observational units which are linked to any of the selected

sampling units are included. Different observational units may be linked to different

numbers of the sampling units. In a survey to estimate the prevalence of a rare disease, for

example, a random sample of medical centres might be selected. From the records of each

medical centre in the sample, records of the patients treated for the disease of interest could

be extracted. A given patient may have been treated at more than one centre and the more

centres at which treatment has been received, the higher the

inclusion probability

for the

patient’s records. [Aids, 1996, 10, 657–66.]

Neural networks: See artiﬁcial neural networks.

N ewman^ Keuls test: A

multiple comparison test

used to investigate in more detai l the differ-

ences existing between a set of means as indicated by a signiﬁcant

F-test

in an

analysis of

variance

. The test proceeds by arranging the means in increasing order and calculating the

test statistic

S ¼







ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



where



and



are the two means being compared, s

is the within groups mean square

from the analysis of variance, and n

and n

are the number of observations in the two

groups. Tables of critical values of S are available, these depending on a parameter r that

speciﬁes the interval between the ranks of the two means being tested. For example, when

comparing the largest and smallest of four means, r = 4, and when comparing the second

smallest and smallest means, r = 2. [SMR Chapter 9.]

Newton ^ Raphso n meth od: A numerical procedure that can be used to optimize (minimize or

maximize) a function f with respect to a set of parameters q

¼½

; ...;

. The iterative

scheme is

iþ1

¼ q

 G

1

ðq

Þgðq

299

where g(θ

) is the vector of derivatives of f with respect to 

; ...;

evaluated at θ

and

G(θ

) is the m × m matrix of second derivatives of f with respect to the parameters again

evaluated at θ

. The convergence of the method is very fast when θ is close to the

optimum but when this is not so G may become negative deﬁnite and the method may fail

to converge. A further disadvantage of the method is the need to invert G on each

iteration. See also Fisher’s scoring method and simplex method.[Introduction to

Optimization Methods and Their Applications in Statistics, 1987, B. S. Everitt,

Chapman and Hall/CRC Press, London.]

Neyman, Jerzy (1894^1981): Born in Bendery, Moldova, Neyman’s paternal grandfather was a

Polish nobleman and a revolutionary who was burned alive in his house during the 1863

Polish uprising against the Russians. His doctoral thesis at the University of Warsaw was

on probabilistic problems in agricultural experiments. Until 1938 when he emigrated to the

USA he had worked in Poland though making academic visits to France and England.

Between 1928 and 1933 he developed, in collaboration with

Egon Pearson

,aﬁrm basis for

the theory of hypothesis testing, supplying the logical foundation and mathematical rigour

that were missing in the early methodology. In 1934 Neyman created the theory of survey

sampling and also laid the theoretical foundation of modern

quality control procedures

.He

moved to Berkeley in 1938. Neyman was one of the founders of modern statistics and

received the Royal Statistical Society’s Guy medal in gold and in 1968 the US Medal of

Science. Neyman died on 5 August 1981 in Oakland, California.

N eyman ^ P earson lemma: An important result for establishing most powerful statistical tests.

Suppose the set of values taken by random variables X

¼½X

; X

; ...; X

 are represented

by points in n-dimensional space (the

sample space

) and associated with each point x is the

value assigned to x by two possible probability distributions P

and P

of X. It is desired to

select a set S

of sample points x in such a way that if P

ðS

Þ¼

x2S

ðxÞ¼α then for

any set S satisfying PðSÞ¼

x2S

ðxÞα one has P

ðSÞP

ðS

Þ. The lemma states that

the set S

¼fx : rðxÞ

Cg is a solution of the stated problem and that this is true for every

value of C where r(x) is the

likelihood ratio

, P

(x)/P

(x). [Testing Statistical Hypotheses, 2nd

edition, 1986, E. L. Lehmann, Wiley, New York.]

Neyman-Rubi n causal framework: A counterfactual framework of causality which is useful

for understanding the assumptions required for valid causal inference under different research

designs. Consider a simple study where either an active treatment (or intervention) T

= 1 or a

control treatment (or intervention) T

= 0 is administered to each unit i. Although each unit is

only given one of the treatments, two “potential outcomes” are denoted Y

(1) if i were given

the active treatment and Y

(0) if it were given the control treatment. The causal effect of

interest is 

¼ Y

ð1ÞY

ð0Þ, but this cannot be estimated since only one of Y

(1) and Y

(0) is

observed. However, under certain assumptions that are explicated in the framework, an

average treatment effect δ can be estimated by

 ¼

E ð Y

¼ 1jT

¼ 1Þ

E ð Y

¼ 1jT

¼ 0Þ.

[Journal of the American Statistical Association, 1986, 81, 945–970.]

Neyman smooth test: A goodness-of-ﬁt test for testing uniformity. [Journal of Applied

Mathematics and Decision Sciences, 2001, 5, 181–191.]

N ightingale, Florence (1 820^1910): Born in Florence, Italy, Florence Nightingale trained as a

nurse at Kaisersworth and Paris. In the Crimean War (1854) she led a party of 38 nurses to

organize a nursing department as Scutari, where she substantially improved the squalid

hospital conditions. She devoted much of her life to campaigns to reform the health and

living conditions of the British Army, basing her arguments on massive amounts of data

carefully collated and tabulated and often presented in the form of

pie charts

and

bar charts

300

Ahead of her time as an epidemiologist, Florence Nightingale was acutely aware of the need

for suitable comparisons when presenting data and of the possible misleading effects of

crude death rates. Well known to the general public as the Lady of the Lamp, but equally

deserving of the lesser known alternative accolade, the Passionate Statistician, Florence

Nightingale died in London on 13 August 1910.

NLM: Abbreviation for non-linear mapping.

NOEL: Abbreviation for no-observed-effect level.

N of 1 clinical trial: A special case of a

crossover design

aimed at determining the efﬁcacy of a

treatment (or the relative merits of alternative treatments) for a speciﬁc patient. The patient is

repeatedly given a treatment and placebo, or different treatments, in successive time periods.

See also interrupted time series design.[Statistical Issues in Drug Development, 2nd

edition, 2008, S. Senn, Wiley-Blackwell, Chichester.]

Nofreelunchtheorem: A theorem concerned with optimization that states (in very general terms)

that a general-purpose universal optimization strategy is theoretically impossible, and the

only way one strategy can outperform another is if it is specialized to the speciﬁc problem

under consideration. [Complexity, 1996, 1,40–46.]

Noise: A

stochastic process

of irregular ﬂuctuations. See also white noise sequence.

N omi nal signi ficance level: The signiﬁ cance level of a test when its assumptions are valid.

Nominal variable: Synonym for unordered categorical variable.

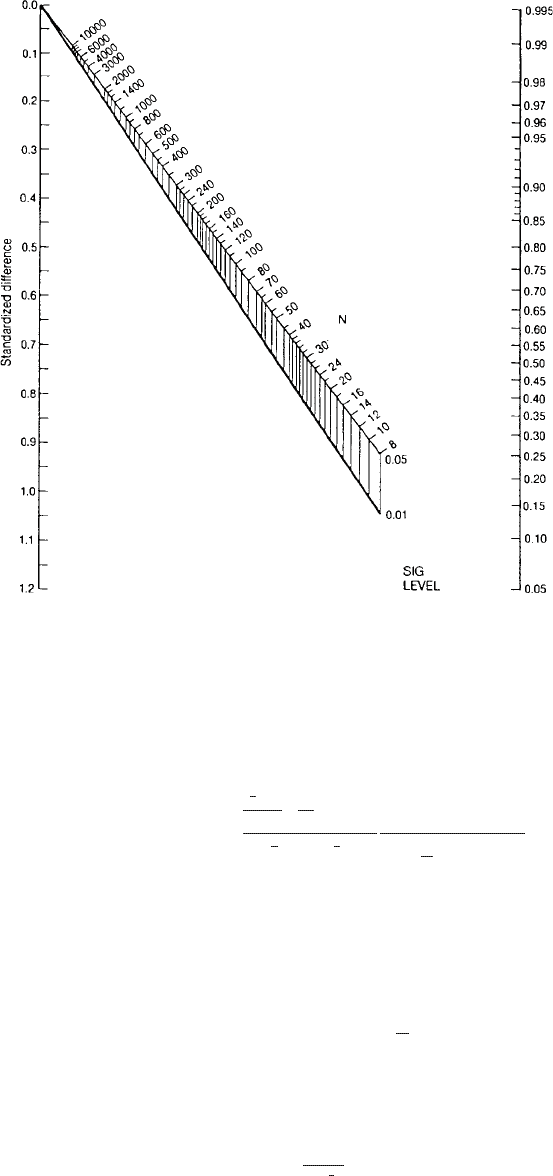
Nomogram: Graphic method that permit the representation of more than two quantities on a plane

surface. The example shown in Fig. 97 is of such a chart for calculating sample size or

power. [SMR Chapter 15.]

Noncentral chi-squared distribution: The probability distribution, f(x), of the sum



i¼1

ðZ

þ 

where Z

; ...; Z



are independent standard normal random variables and 

; ...;



are

constants. The distribution has degrees of freedom  and is given explicitly by

f ðxÞ¼

ðxþlÞ=2

ð2Þ=2

=2

r¼0

r!ð

 þ rÞ

where l ¼



i¼1



is known as the noncentrality parameter. Arises as the distribution of

sums of squares in

analysis of variance

when the hypothesis of the equality of group means

does not hold. [KA2 Chapter 23.]

Noncentral distributions: A series of probability distributions each of which is an adapta-

tion of one of the standard

sampling distributions

such as the

chi-squared distribu-

tion

,the

F-distribution

Student’s

t-distribution for the distribution of some test

statistic under the alternative hypothesis. Such distributions allow the

power

of the

corresponding hypothesis tests to be calculated. See also noncentral chi-squared

distribution, noncentral F-distribution and noncentral t-distribution. [KA2

Chapter 23.]

301

Noncentral F-distribution: The probability distribution of the ratio of a random variable having a

noncentral chi-squared distribution

with noncentrality parameter λ divided by its degrees of

freedom (

), to a random variable with a

chi-squared distribution

also divided by its degrees

of freedom (

). Given explicitly by

f ðxÞ¼e

l=2

r¼0

lÞ





ð

=2Þþr

Bð



þ r;



ð

=2Þþr1

1 þ





rþð

þ

Þ=2

where B is the

beta function

. The doubly noncentral F-distribution arises from considering

the ratio of two noncentral chi-squared variables each divided by their respective degrees of

freedom. [KA2 Chapter 23.]

Noncentralhypergeometric distribution: A probability distribution constructed by suppos-

ing that in

sampling without replacement

, the probability of drawing say a white ball, given

that there are X′ white and N′ − X′ black balls is not

but X

½X

þ ðN

 X

Þ

1

with

 6¼ 1. [Univariate Discrete Distributions, 2005, N. L. Johnson, A. W. Kemp and S. Kotz,

Wiley, New York.]

Noncentral t-distribution: The probability distribution, f(x), of the ratio

Z þ 

Fig. 97 A nomogram for calculating sample size.

302

where Z is a random variable having a standard normal distribution and W is independently

distributed as 

= with  degrees of freedom; δ is a constant. Given explicitly by

f ðxÞ¼fð

Þð

Þ

1=2

expð



Þg

1

r¼0

fð2=Þ

1=2

xg

f

ð þ r þ 1Þg

1 þ





ðþrþ1Þ=2

[KA2 Chapter 23.]

Non-compliance: See protocol violations.

N o nd i fferent ia l measu rement err or: When the measurement error for a fallibly measured

covariate in a regression model is conditionally independent of the outcome, given the true

covariate. [American Journal of Epidemiology, 1991, 134, 1233–1246.]

No n-Gaussian time series:

Time series

, often not

stationary

with respect to both mean and

period, which exhibit a non-Gaussian random component. [Biometrics, 1994, 50, 798–812.]

No n-identified response A term used to denote

censored observations

survival data

, that are

not independent of the endpoint of interest. Such observations can occur for a variety of

reasons:

Misclassiﬁcation of the response; e.g. death from cancer, the response of interest,

being erroneously misclassiﬁed as death from another unrelated cause.

Response occurrence causing prior censoring; e.g. relapse to heroin use causing a

subject to quit a rehabilitation study to avoid chemical detection.

[Biometrics, 1994, 50,1–10.]

Non inferiority trial: See superiority trial.

Non-informative censoring:

Censored observations

that can be considered to have the same

probabilities of failure at later times as those individuals remaining under observation.

[Journal of the American Statistical Association, 1988, 83, 772–9.]

Non-informative prior distribution: A

prior distribution

which is speciﬁed in an attempt to be

non-commital about a parameter, for example, a

uniform distribution

.[Biometrika, 1987, 74,

557–562]

N onl inear mappi ng ( N LM) : A method for obtaining a low-dimensional representation of a set of

multivariate data, which operates by minimizing a function of the differences between the

original inter-individual

Euclidean distances

and those in the reduced dimensional space.

The function minimized is essentially a simple sum-of-squares. See also multidimensional

scaling and ordination .[Pattern Analysis and Applications, 2000, 3,61–68.]

Nonlinear model: A model that is non-linear in the parameters, for example

E ð yj x

; x

Þ¼β

þ β

EðyjxÞ¼β

β

Some such models can be converted into linear models by

linearization

(the second equation

above, for example, by taking logarithms throughout). Those that cannot are often referred

to as intrinsically non-linear, although these can often be approximated by linear equations

in some circumstances. Parameters in such models usually have to be estimated using an

303

optimization procedure such as the

Newton–Raphson method

. In such models linear

parameters are those for which the second partial derivative of the model function with

respect to the parameter is zero (β

and β

in the ﬁrst example above); when this is not the

case (β

and β

in the ﬁrst example above) they are called non-linear parameters. [ARA

Chapter 14.]

Nonlinear regression: Synonym for non-linear model.

Nonlinear time series: See time series.

Nonmasked study: Synonym for open label study.

Nonmetric scaling: A form of

multidimensional scaling

in which only the ranks of the observed

dissimilarity coefﬁcients

similarity coefﬁcients

are used in producing the required low-

dimensional representation of the data. See also monotonic regression. [MV1 Chapter 5.]

N onnegative garrotte: An approach to choosing subsets of explanat ory variables in regression

problems tha t eliminates some variables, ‘shrinks’ the regression coefﬁcients of others

(similar to what happens in

ridge regression

), and gives relatively stable results unlike

many of the usual subset selection procedures. Th e method operates by ﬁnding fc

g to

minimize



where f

gare the results of

least squares estimation

, and y and x represent the response and

explanatory variables. The fc

g satisfy the constraints;

 0

 s

The new regression coefﬁcients are

ðsÞ¼c

. As the garrotte is drawn tighter by

decreasing s, more of the fc

g become zero and the remaining non-zero

ðsÞ are shrunken.

In general the procedure produces regression equations having more non-zero coefﬁcients

than other subset selection methods, but the loss of simplicity is offset by substantial gains in

accuracy. [Technometrics, 1995, 37, 373–84.]

Non parametric Bayesian models: Models used in

Bayesian inference

that do not commit a

prior distribution

to a particular number of parameters; instead the data is allowed to dictate

how many parameters there are. Possible

overﬁtting

is prevented by integrating out all

parameters and latent variables. [Bayesian Data Analysis, 2nd edn, 2003, A.Gelman,

J. B. Carlin, H. S. Stern and D. B. Rubin, Chapman and Hall/CRC, Boca Raton.]

Non parametric maximum likeli hood (N PML): A

likelihood

approach which does not require

the speciﬁcation of a full parametric family for the data. Usually, the nonparametric maximum

likelihood is a multinomial likelihood on a sample. Simple examples include the empirical

cumulative distribution function and the

product-limit estimator

. Also used to relax parametric

assumptions regarding random effects in

multilevel models

. Closely related to the

empirical

likelihood

.[Journal of the American Statistical Association, 1978, 73,805–811.]

Non-orthogonal designs:

Analysis of variance

designs with two or more factors in which the

number of observations in each cell are not equal.

Non parametric analysis of covariance: An

analysis of covariance

model in which the cova-

riate effect is assumed only to be ‘smooth’ rather than of some speciﬁc linear or perhaps non-

linear form. See also kernel regression smoothing.[Biometrics, 1995, 51, 920–31.]

304

Nonparametric methods: See distribution free methods.

Nonparametric regression modelling: See regression modelling .

N on-randomized cl in ical tria l: A

clinical trial

in which a series of consecutive patients receive a

new treatment and those that respond (according to some pre-deﬁned criterion) continue to

receive it. Those patients that fail to respond receive an alternative, usually the conventional,

treatment. The two groups are then compared on one or more outcome variables. One of the

problems with such a procedure is that patients who respond may be healthier than those

who do not respond, possibly resulting in an apparent but not real beneﬁt of the treatment.

[Statistics in Medicine, 1984, 3, 341–6.]

Non-response: A term generally used for failure to provide the relevant information being collected

in a survey. Poor response can be due to a variety of causes, for example, if the topic of the

survey is of an intimate nature, respondents may not care to answer particular questions.

Since it is quite possible that respondents in a survey differ in some of their characteristics

from those who do not respond, a large number of non-respondents may introduce bias into

the ﬁnal results. See also item non-response. [SMR Chapter 5.]

No-observed-effect level (NOEL): The dose level of a compound below which there is no

evidence of an effect on the response of interest. [Food and Chemical Toxicology, 1997, 35,

349–55.]

Norm: Most commonly used to refer to ‘what is usual’, for example, the range into which body

temperatures of healthy adults fall, but also occasionally used for ‘what is desirable’, for

example, the range of blood pressures regarded as being indicative of good health.

Normal approximation: Normal distributions that approximate other distributions; for example, a

normal distribution with mean np and variance np(1 − p) that acts as an approximation to a

binomial distribution

as n, the number of trials, increases. The term, p represents the

probability of a ‘success’ on any trial. See also DeMoivre–Laplace theorem.[Handbook

of the Normal Distribution, 1996, J. K. Patel and C. B. Read, CRC, Boca Raton.]

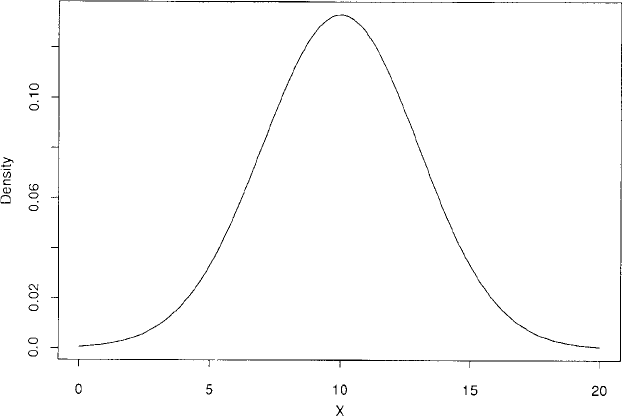
Normal distribution: A probability distribution, f(x), of a random variable, X, that is assumed

by many statistical methods. Speciﬁcally given by

f ðxÞ¼



ﬃﬃﬃﬃﬃﬃ

exp 

ðx Þ



where µ and σ

are, respectively, the mean and variance of x. This distribution is

bell-shaped

as shown in the example given in Fig. 98. [STD Chapter 29.]

Normal equations: The linear equations arising in applying

least squares estimation

to determining

the coefﬁcients in a linear model.

N ormal equ ival ent deviate: A value, x

, corresponding to a proportion, p, that satisﬁes the

following equation

1

ﬃﬃﬃﬃﬃﬃ

exp

u



du ¼ p

Also known as the normit. See also probit analysis.

305

Normality: A term used to indicate that some variable of interest has a normal distribution.

N ormal probabi lity pl ot: See probability plot.

N o rmal range: Synonym for reference interval.

Normal scores: The expectations of the order statistics of a sample from the standard normal

distribution. The basis of

probability plots

.[Biometrika, 1961, 48, 151–65.]

Normal scores test: An alternative to the

Mann–Whitney test

for comparing populations under

shift alternatives. [Practical Nonparametric Statistics , 1980, W. J. Conover, Wiley, New

York.]

Normit: See normal equivalent deviate.

NORMIX: A computer program for the

maximum likelihood estimation

of the parameters in a

ﬁnite

mixture distribution

in which the components are

multivariate normal distributions

with

different mean vectors and possibly different

variance–covariance matrices

. [http://alumnus.

caltech.edu/~wolfe/normix.htm]

nQuer y advisor: A software package useful for determining sample sizes when planning research

studies. [Statistical Solutions Ltd., 8 South Bank, Crosse’s Green, Cork, Ireland; Stonehill

Corporate Center, Suite 104, 999 Broadway, Saugus, MA 01906, USA.]

Nuisance parameter: A parameter of a model in which there is no scientiﬁc interest but whose

values are usually needed (but in general are unknown) to make inferences about those

parameters which are of such interest. For example, the aim may be to draw an inference

about the mean of a normal distribution when nothing certain is known about the variance.

The

likelihood

for the mean, however, involves the variance, different values of which will

lead to different likelihood. To overcome the problem, test statistics or estimators for the

parameters that are of interest are sought which do not depend on the unwanted parameter(s).

See also conditional likelihood. [KA2 Chapter 20.]

N ull distri bution: The probability distribution of a test statistic when the null hypothesis is true.

Fig. 98 A normal distribution with mean 10 and variance 9.

306

Null hypothesis: Typically, the ‘no difference’ or ‘no association’ hypothesis to be tested (usually by

means of a signiﬁcance test) against an alternative hypothesis that postulates non-zero

difference or association.

Null matrix : A matrix in which all elements are zero.

Null vector : A vector the elements of which are all zero.

Number needed to treat: The reciprocal of the reduction in absolute risk between treated and

control groups in a

clinical trial

. It is interpreted as the number of patients who need to be

treated to prevent one adverse event. [British Medical Journal, 1995, 310, 452–4.]

N u mbernumbn ess: The inability to fathom, compare or appreciate very big or very small numbers.

[Chance Rules, 2nd edn, 2008, B. S. Everitt, Springer, New York.]

Nu mbe r of part iti ons: A general expression for the number of partitions, N,ofn individuals or

objects into g groups is given by

N ¼

i¼1

ð1Þ

gi



For example, when n = 25 and g = 4, then N is 45 232 115 901. [Introduction to

Combinatorial Mathematics, 1968, G. L. Liu, McGraw-Hill, New York.]

Numerical integration: The study of how the numerical value of an integral can be found. Also

called

quadrature

which refers to ﬁnding a square whose area is the same as the area under a

curve. See also Simpson’s rule, Gaussian quadrature and trapeziodal rule.[Methods of

Numerical Integration, 1984, P. J. Davis and P. Rabinowitz, Academic Press, New York.]

N umerical taxonomy: In essence a synonym for cluster analysis.

Nuremberg code: A list of ten standards for carrying out clinical research involving human subjects,

drafted after the trials of Nazi war criminals at Nuremberg. See also Helsinki declaration.

[Trials of War Criminals before the Nuremberg Military Tribunals Under Control Council

Law No 10, volume 2, 1949, 181–182, Washington DC, US Government Printing Ofﬁce.]

Nyquist frequency: The frequency above which there is no information in a continuous

time series

which has been digitized by taking values at time intervals δt apart. Explicitly the frequency

is 1/2 δt cycles per unit time.

307

Oblique factors: A term used in

factor analysis

for

common factors

that are allowed to be

correlated. [Psychometrika, 2003, 68, 299–321.]

O’Brien ^ Fleming method: A method of

interim analysis

in a

clinical trial

in which very small

p-values are required for the early stopping of a trial, whereas later values for stopping are

closer to conventional levels of signiﬁcance. [Statistics in Medicine, 1994, 13, 1441–52.]

O’Brien’s two-sample tests: Extensions of the conventional tests for assessing differences

between treatment groups that take account of the possible heterogeneous nature of the

response to treatment and which may be useful in the identiﬁcation of subgroups of patients

for whom the experimental therapy might have most (or least) beneﬁt. [Statistics in

Medicine, 1990, 9, 447–56.]

Observational study: A study in which the objective is to uncover cause-and-effect relationships

but in which it is not feasible to use controlled experimentation, in the sense of being able

to impose the procedure or treatments whose effects it is desired to discover, or to assign

subjects at random to different procedures. Surveys and most epidemiological studies fall

into this class. Since the investigator does not control the assignment of treatments there is

no way to ensure that similar subjects receive different treatments. The classical example

of such a study that successfully uncovered evidence of an important causal relationship

is the smoking and lung cancer investigation of

Doll

and

Hill

. See also experimental

study, prospective study and retrospective study. [SMR Chapter 5.]

Observat i on-d ri ven model: A term usually applied to models for

longitudinal data

time

series

which introduce within unit correlation by specifying the

conditional distribution

an observation at time t as a function of past observations. An example is the

ante-

dependence model

. In contrast in a parameter-driven model,

correlation

is introduced

through a latent process, for example, by introducing a random subject effect. [Biometrika,

2003, 90, 777 –90.]

Observed-score equating: The practice of transforming observed scores on different forms

of (usually) a cognitive test to a common normal distribution. [Test Equating, 1982, edited

by P. W. Holland and D. B. Rubin, Academic Press, New York.]

Obuchowski and Rockette method: An alternative to the

Dorfman–Berbaum–Metz method

for analyzing multiple reader

receiver operating curve

data. Instead of modelling the

jack-

knife

pseudovalues, in this approach a mixed-effects

analysis of variance

model is used

to model the accuracy of the jth reader using the ith diagnostic test. [Communications in

Statistics; Simulation and Computation, 1995, 24, 285–308.]

Occam’srazor:An early statement of the

parsimony principle

, given by William of Occam

(1280–1349) namely ‘entia non sunt multiplicanda praeter necessitatem’; i.e. ‘A plurality

(of reasons) should not be posited without necessity’. In other words one should not

make more assumptions than the minimum needed. The concept underlies all scientiﬁc

308