Евдокимова Н.Н. Алгебра и начала анализа в таблицах и схемах
Подождите немного. Документ загружается.

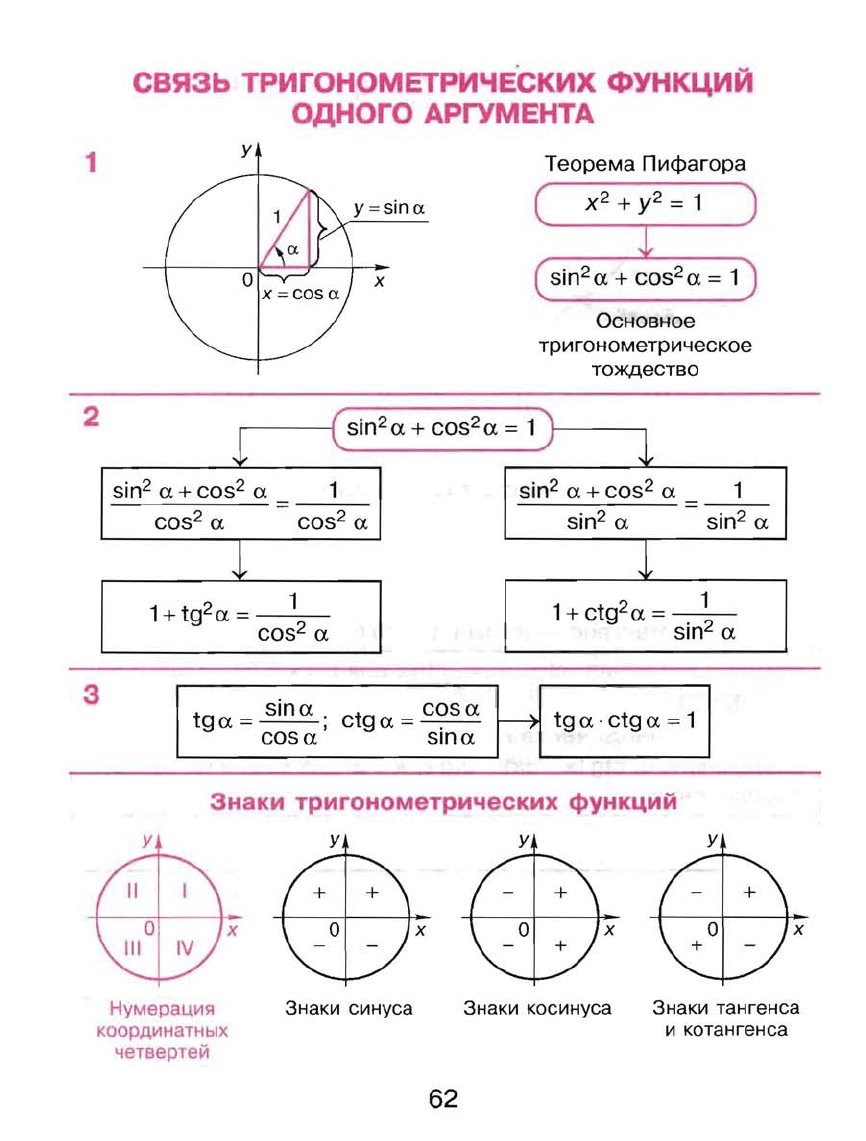
2
связь
ИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ
ОДНОГО
АРГУМЕНТА
Теорема
Пифагора
1
у
у
=sin
а
х
2
+
у2
= 1
х
Основное
тригонометрическое
тождество
sin
2
a +
cos
2
a =
1)
1 1
sin
2
а
+
cos
2
а
1
sin
2
а
+
cos
2
а
1
=
=
cos
2
а
cos
2
а
sin
2
а
sin
2
а
1
1
1
1
1+
ctg
2
a =
1+tg
2
a=
sin
2
а
cos
2
а
з
tga
=
sina
;
ctga
=
c~sa
COSa
slna
~
tga·
ctga
= 1
Эна
и
тригонометрических
функций
у у у у
х
Нумерация
Знаки
синуса
Знаки
косинуса
Знаки
тангенса
коорди
натн
ых
и
котангенса
четвер
ей
62

ПРИМЕРЫ
ПРИМЕНЕНИЯ
ФОРМУЛ
Если
известна
одна
из
тригонометрических
функций,
то,
используя
формулы,
можно
вычислить
все
остальные
тригонометрические
функ
ции
угла,
учитывая
в
какой
четверти
лежит
заданный
угол.
. t 3
sln
=--
5
1t <t <
3п
2
угол
t
лежит
в
111
четверти
2
COS
2
t = 1- sin
2
t = 1_ (l) = 25 -
~
= .!§..
5 25 25
25'
COS
t =
-~
=
-~
,
Т. к.
косинус
В
111
четверти
отри
цателен.
tgt
=
:~~tt
=
(-~):
(-~)=
t;
ctgt
=
t~t
=~.
4 3 4
cos t = -
5";
tg
t =
4;
ctg
t =
З'
~
~
~
1
cosa
= 3
а
Е
[З
2
п;
2п
]
угол
а
лежит
в
IV
четверти
·
CJ
9 1 8
sln
2
а
= 1- cos
2
а
= 1-
3"
=
9"
-
9"
=
9";
sina
=
-~
= -
2.;2
,
т.
к.
синус
В
IV
четверти
отри
9 3
цателен.
tga=
sina
=_2.;2
:~=-2.;2;
ctga=_1_=
__
1_=_
.;2.
cosa
3 3
tga
2J2
4
·
2J2
J2
.;2
Slпа
=
--3-;
tgo. =
-2
2; ctga. =
-4'
~
~
~
tg
Х
=
-10
1t
2<х<п
угол
Х
лежит
воltчетверти
2_
1 _ 1
_1.
_ 1
cos
Х
- 1+
tg2
Х
- 1+100 - 101' cos
Х
- - .J101'
т.
к.
косинус
во
11
четверти
отрицателен.
· 10
sinx
slnx
=
tgxcosx
=
.J101'
т.
к.
tgx
=--.
101
cosx
1 1
ctgx
=
--
=
--о
tgx
10
1 . 1
О
1
cosx
=-
.J101;
SIПХ
= .J101;
ctgx
=-10'
~
~
~
4
63

n
РИОДИЧНОСТЬ
ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ
Z'
А
-~i'
-yJ-j-;
coso
~O
Pt(X;
у)
Х
=cos<X
у
= sin
ct
Ч
sin
а
= sin
(а
+
2м),
cos
а
=
cos
(а
+ 21tk) ,
k
=
О;
±1, ±2, ...
~
tg
а
=
tg
(а
+ 1tk),
ctg
а
=
ctg
(а
+ 1tk),
k
=
О;
±1, ±2, ...
Вращательное
движение
точки
P
t
по
окружности
-
процесс
перио-
дический.
Тригонометрические
функции
определены
с
помощью
координат
вращающейся
точки,
поэтому
все
тригоно
етриче-
ские
функции
периодические.
Функции
sin
а,
cos
а
являются
периодическими
с
периодом
~
2п
= 360°.
Функции
tg
а,
ctg
а
являются
периодическими
с
периодом
I~
1t
= 180°.
Число
k
показывает
целое
число
оборот
в,
пройденное
точкой,
причем
если
k -
положительное
(k
>
О),
то
точка
двигается
против
часовой
стрелки.
если
k -
отрицательное
(k
<
О),
то
точка
двигается
по
часовой
стрелке.
При
меры
1.
Найти
sin 765°.
sin 765° = sin
(2·360°
+ 45°) = sin 450 =
J2
2
Делим
765°
на
360°:
получаем
2
и
остаток
45°.
Ответ:
J2
2'
2.
Найти
cos(-11700).
cos (-1170°) =
cos
1170° =
cos
(3 . 360° + 90°) =
cos
90° =
О
Знак
«-»
опускаем,
т.
к.
функция
косинус
четная.
Ответ:
О.
64

ЧЕТНОСТЬ
И
Н
ЕЧЕТНОСТЬ
ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ
sin
(-а)
=
-sin
а
Функции
sin
а,
tg
а,
ctg
а
являются
f---)
tg
(-а)
=
-tg
а
нечетными.
ctg
(-а)
=
-ctg
а
Функция
cos
а
является
четной.
cos
(-а)
=
cos
а
Примеры.
cos
(-390°)
=
cos
390° =
cos(360°
+ 30°) =
cos
300
=
JЗ
;
2
sin(-600)
=
-sin60°
= -
~;
tg
(-750°)
=-
tg750°
=-
tg
(4
·180° + 30°) =- tg 30° =- : ;
ctg
(-210°)
=
-ctg
210° =
-ctg
(180° + 30°) =
-ctg
30° =
-JЗ.
ФОРМУЛЫПРИВ~ЕНИЯ
1t
3п
Тригонометрические
2п
±
(Х
могут
быть
выражены
мул
приведения.
'"
Sin(~+(X
)=cos(x
'"
cos(3
1t
-
(Х
)=
-siп(Х
2
tg(1t +
(Х)
=
tg(X
ctg
(З
2
п
-
(Х
) =
tg(X
cos(
1t
+
(Х)
= -
cos
(Х
и
т.
д.
функции
углов
вида
2"
±
(Х;
1t
±
(Х;
2 ±
(Х
и
через
функции
угла
(Х
с
помощью
фор-
Правило
формул
приведения
1.
Для
углов
л
±
(Х
и
2л
±
а
название
исходной
функции
сохраняется.
Для
углов
~±
а
и
3
2
л
±
(j
название
исходной
функции
заменяется
(си-
нус
на
косинус,
косинус
на
синус,
тангенс
на
котангенс,
котангенс
на
тангенс).
11.
Функция
в
правой
части
ра-
венства
берется
с
тем
же
знаком,
какой
имеет
исходная
функция.
Угол
а
-
считать
острым.
i
65

Примеры
использования
формул
приведения
Ilриведите
к
тригонометрической
функ-
ции
угла
сх.
1t 1t
-+сх
--сх
2
л
2
1I:-CX
211:+
сх
У+2
......
.--
11
n:
О
111
3л
I
121r
х
т
---
IV
1t
сх
3п
2
-+а.
3п
2
--сх
2п
-сх
2
Синус
во
11
четверти
положителен.
-1'
±
SIП
.
{п
2"
+
сх
:::
+coscx
~
-т-
Функция
заменяется
С
синуса
на
косинус.
Котангенс
угла
во
11
четверти
отрицателен.
1-
±
ctg
(п-сх):::
-ctg
сх
"f
J
I
Функция
сохраняет
название.
I
ФОРМУЛЫ
СЛОЖЕНИЯ
1.
Формулы
синуса
суммы
и
разности
двух
аргументов:
sin(a
+
~)
=
sinacos~
+
cosasin~
sin(a
-
~)
=
sinacos~
-
cosasin~
2.
Формулы
косинуса
суммы
и
разности
двух
аргументов:
cos(a
+
~)
=
cosacos~
-
sinasin~
cos(a
-
~)
=
cosacos~
+
sinasin~
з.
Формулы
тангенса
суммы
и
разности
двух
аргументов:
tg(a
+~)
=
tga
+
tg~
1-
tga
tg~
tg(a
_~)
=
tga
-
tg~
1+
tga
tg~
66

4.
Формулы
котангенса
суммы
и
разности
двух
аргументов:
ctg(a
+~)
=
1-
tga
tg~
tga
+
tg~
ctg(a
_~)
= 1+
tga
tg~
tga-
tg~
Формулы
сложения
ДЛЯ
кратных
аргументов
sin2a
=
sin(a
+
а)
=
sinacosa
+
cosasina
=
2sinacosa
sin2a
=
2sinacosa
cos2a
= cos
2
a - sin
2
a = 1 - 2sin
2
a = 2cos
2
a - 1
tg2a
=
2tga
1-
tg
2
a
ctg2a
=
2ctg
2
a
-1
2ctga
siпЗа
=
Зsiпа
-
4siп
З
а
cos
За
=
4соs
З
а
-
Зсоs
а
Для
функций
половинного
аргумента
имеют
место
следу
ющие
соотношения
(знак
«+»
или
«-»
выбирается
в
соответ
ствии
с
тем,
в
какой
четверти
координатной
плоскости
(квад
а
ранте)
находится
угол
-
аргумент
2"):
·па
_+~1-cosa
Sl
--
2 - 2
cos
~
=
±~1
+ c
2
0sa
tg
а
=+ 11-
cos
а
= sin
а
2 - 1+
cos
а
1+ cos
а
=
1-
cos
а
sin
а
ctga
=±
/1+cosa
=
sina
2
1-cosa
1-cosa
=
1+cosa
sina
67

Формулы
сложения
для
суммы
и
разности
функций
. .
~
2'
a+~
a-~
Slпа
+
SIП
=
SIП-
2
-СОS-
2
-
. .
~
2
a+~.
a-~
Slпа-SIП
=
СОS-
2
-SIП-
2
-
a+~
a-~
cos
а
+
cos
~
= 2
cos
-2-
cos
-2-
~
2'
a+~
.
a-~
cosa-cos
= -
SIП--SIП--
2 2
cos
а
±
siп
а
=
.J2
siп
(
~
±
а
) =
.J2
cos
(
~
±
а
)
t
a±t
~
=
siп(а±~)
9 9
cosacos~
siп(а
±~)
ctg
а
±
ctg
~
=
±.
.
SlпаSIП~
ct
а
_ t
~
= cos(
а
+
~)
9 9
siпасоs~
cos(a
-~)
tga
±
ctg~
= .
соsаSIП~
ПРОИЗВЕДЕНИЯ
ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ
siпаsiп~
=
~
[cos(a
-~)
-
cos(a
+
~)]
cos
а
cos
~
=
~
[cos(
а
-
~)
+ cos(
а
+
~)]
siпасоs~
=
~
[siп(а
-~)
+
siп(а
+
~)]
соsаsiп~
=
~[Siп(а
+~)
-
siп(а
-
~)]
68
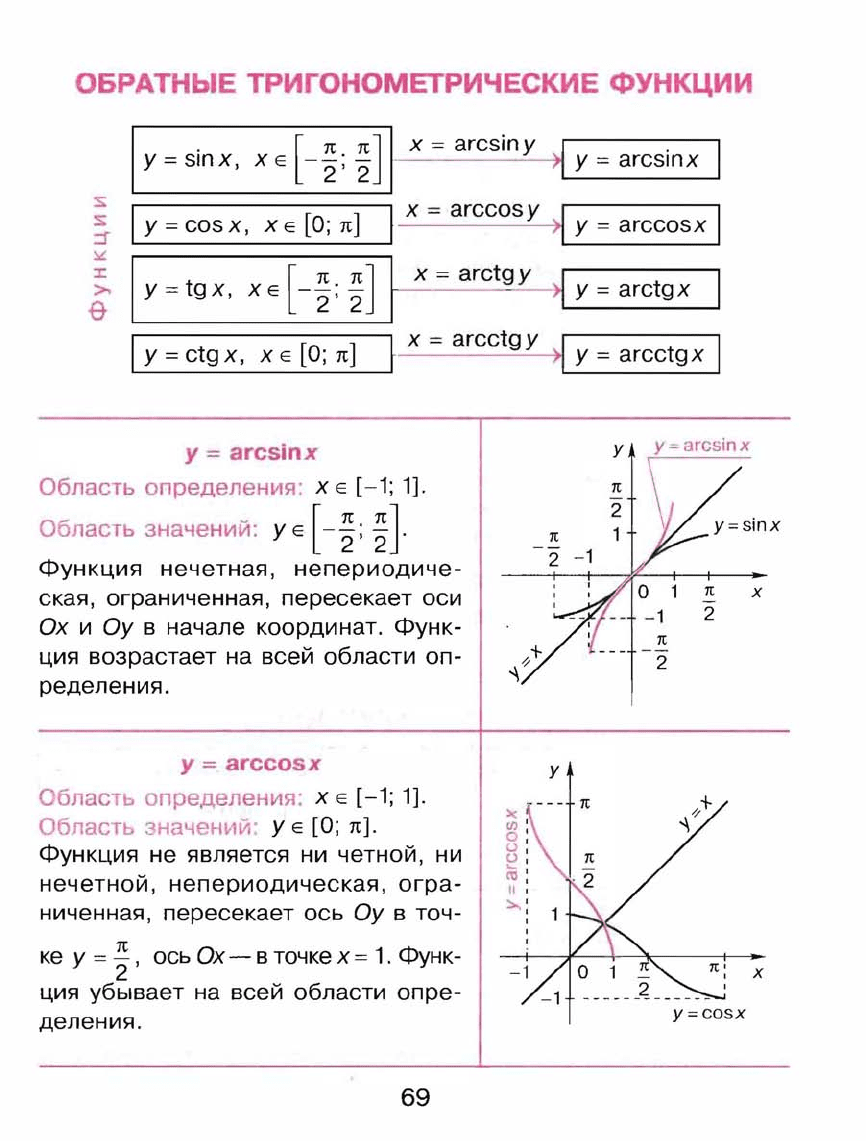
ОБРАТНЫЕ
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
1·
[
1t
п]
I
х
~
arcsiny
I . I
у
= SlnX,
Х
Е
-2";
2"- >
у
=
arcslnx
:s:
I I
Х
=
arccos
у
I I
;.
у
=
COSX,
Х
Е
[О;
п]
>
У
=
arccosx
~
1t 1t
Х
=
arct
.е
у
=
tg
Х,
Х
Е
[-2";
2"]
gy
>1
у
=
arctgx
I
~
х
=
arcctg
у
I
~
I I
у
=
ctgx,
х
Е
[О;
п]
>
У
=
arcctgx
у
=
arcsinx
Область
определения'
х
Е
[-1;
1].
Область
значений:
у
Е
[-~;
~].
Функция
нечетная,
непериодиче
екая,
ограниченная,
пересекает
оси
Ох
и
Оу
в
начале
координат.
Функ
ция
возрастает
на
всей
области
оп
ределения.
у
=
arCC05X
Область
определения:
х
Е
[-1;
1].
Область
значений
у
Е
[О;
п].
Функция
не
является
ни
четной,
ни
нечетной,
непериодическая,
огра
ниченная,
пересекает
ось
Оу
в
точ
ке
у
=
~,
ось
Ох-
в
точке
Х=
1.
Функ
ция
убывает
на
всей
области
опре
деления.
у
1t
х
х
y=cosx
69
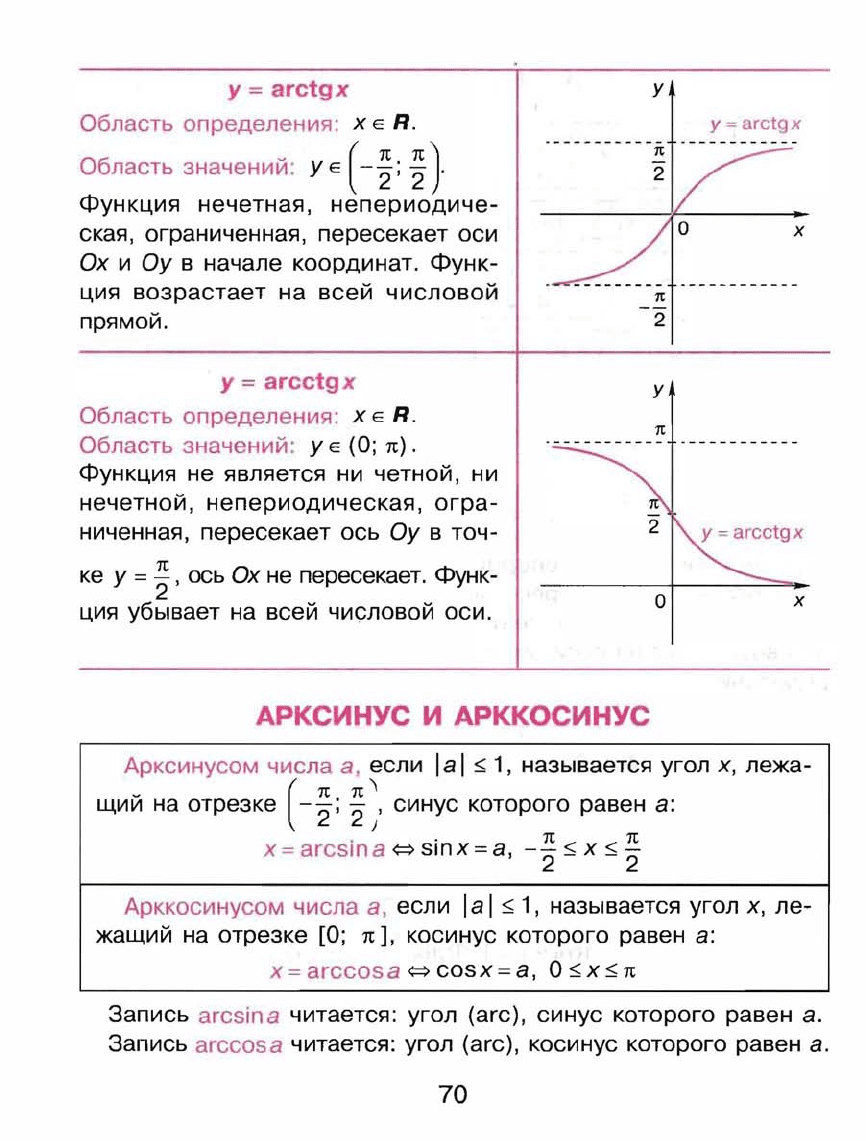
------------ ------------
у
=
arctgx
Область
определения:
х
Е
R.
Область
значений'
у
Е
( -
;;
;)-
Функция
нечетная,
непериодиче
екая,
ограниченная,
пересекает
оси
Ох
и
Оу
в
начале
координат.
Функ
ция
возрастает
на
всей
числовой
прямой.
у
=
arcctgx
Область
определения:
х
Е
R.
Область
значений:
у
Е
(О;
п)
.
Функция
не
является
ни
четной,
ни
нечетной,
непериодическая,
огра
ниченная,
пересекает
ось
Оу
в
точ
ке
у
=; ,
ось
Ох
не
пересекает.
Функ
ция
убывает
на
всей
числовой
оси.
у
у
==
arctgx
1t
х
1t
2
у
1t
о
х
АРКСИНУС
И
АРККОСИНУС
Арксинусом
числа
а,
если
1
а
I
~
1,
называется
угол
х,
лежа
~
(
1t
п\
щии
на
отрезке
-
2;
2;'
синус
которого
равен
а:
• .
1t 1t
x=arcslna
~Slnx=a,
-2
~
х
~
2
Арккосинусом
числа
а,
если
la
1
~
1,
называется
угол
х,
ле
жащий
на
отрезке
[О;
п],
косинус
которого
равен
а:
x=arccosa~cosx=a,
O~x~п
Запись
arcsin
а
читается:
угол
(аге),
синус
которого
равен
а.
Запись
arccosa
читается:
угол
(аге),
косинус
которого
равен
а.
70

Основные
тождества
sin
(arcsina)
=
а
cos
(arccosa)
=
а
arcsin
(sinx)
=х,
если
х
Е
[ _
п.
п]
2'2
arccos(cosx)
=х,
если
х
Е
[О;
п]
arcsin(-a)
=-arcsina
arccos
(-а)
= 7t -
arccos
а
Примеры
.
.( .
1)
.
(п)
1
SIП
аГСSIП
2 =
SIП
"6
= 2
агсsiпО
=
О
агсsiп.1.
_ 1t
cos(
arccos~)
=
cos(
~)
=
~
2-"6
.
(.
п)
.
(1)
_1t7t
arccos
.JЗ
аГСSIП
SIП"6
=
аГСSIП
2
="6
2
-"6
1.(
п)
. 7t
arccos(-
1)
= 1t
аГСSIП
-"6
=
-аГСSIП"6
=-2
1)
1 7t
2п
arccos
-2
= 1t -
arccos
=
1t
- 3 = 3
агсsiп
1=
2:.
(
2 2
АРКТАНГЕНС
И
АРККОТАНГЕНС
Арктангенсом
числа
а
называется
угол
х
Е
[-;;
;]
тангенс
которого
равен
а:
х
=
arctga
Арккотангенсом
числа
а
называется
угол
х
Е
{О;
п],
ко
тангенс
которого
равен
а:
х
=
arcctga
Основные
тождества
tg(arctga)
=
а
ctg
(arcctg
а)
=
а
arctg
(tgx)
=
х,
если
х
Е
[ _
п.
п]
2'2
arcctg(ctgx)
=х,
если
х
Е
[О;
п]
arctg
(-х)
=
-arctgx
arcctg
(-х)
= 7t -
arcctgx
71
