Евдокимова Н.Н. Алгебра и начала анализа в таблицах и схемах
Подождите немного. Документ загружается.

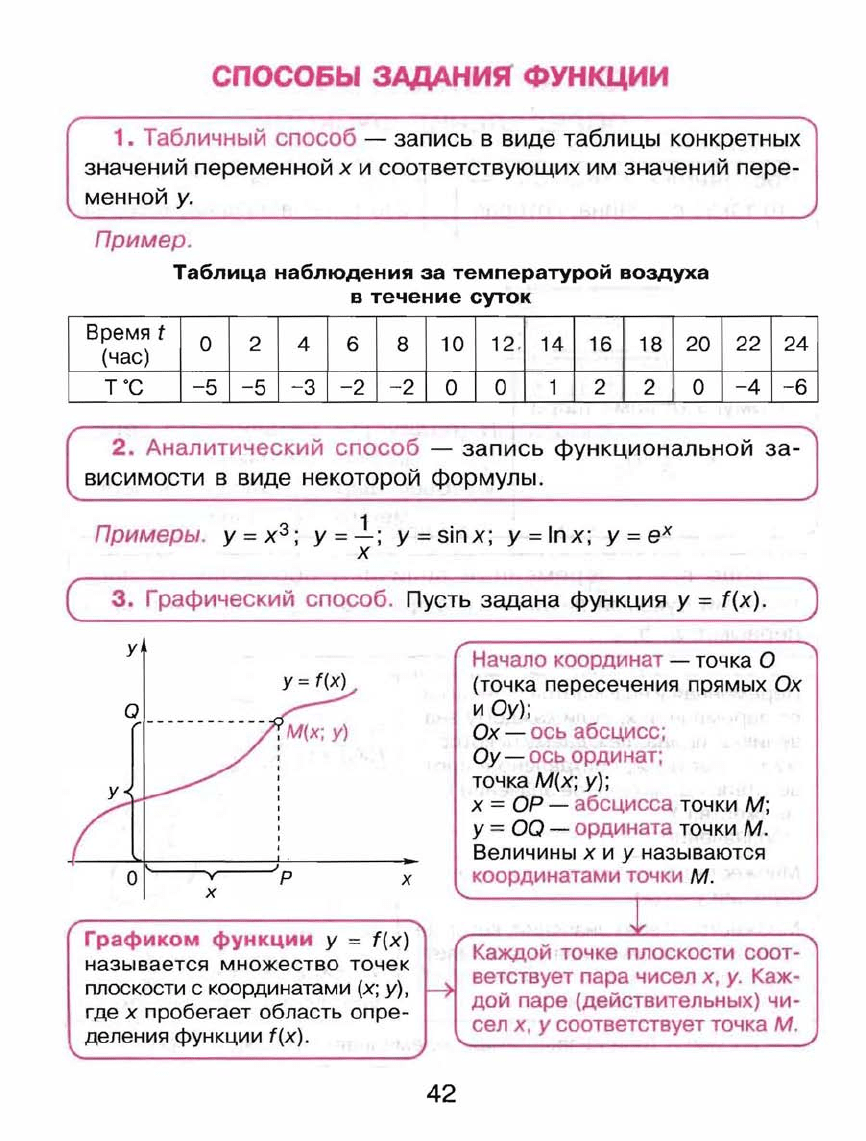
СПОСОБЫ
ЗАДАния
функции
1.
Табличный
способ
-
запись
в
виде
таблицы
конкретных
значений
переменной
х
и
соответствующих
им
значений
пере
мен
ной
у.
Пример.
Таблица
наблюдения
за
температурой
воздуха
в
течение
суток
Время
t
(час)
О
2 4 6
8
10
12.
14
16118
I
20 22
24
т·е
-5
-5
-3
-2 -2
О О
1
2
11
2
о
-4
-6
2.
Аналитический
способ
-
запись
функциональной
за
висимости
в
виде некоторой
формулы.
Примеры.
у
=
х
З
;
у
=
1;
у
=
sinx;
у
=
Inx;
у
=
е
Х
х
з.
Графический
способ.
Пусть
задана
функция
у
=
f(x).
у
Q
у
х
Графиком
функции
у
=
f(x)
называется
множество
точек
плоскости
с
координатами
(х;
у),
где
х
пробегает
область
опре
деления
функции
f(x).
o'-y--lp
х
Начало
координат
-
точка
О
(точка
пересечения
прямых
Ох
и
ау);
Ох
-
ось
абсцисс;
ау
-
ось
ординат;
точка
М(х;
у);
х
=
ОР
-
абсцисса
точки
М;
у
=
00
-
ордината
точки
М.
Величины
х
и
у
называются
координатами
точки
М.
Каждой
точке
плоскости
соот
ветствует
пара
чисел
х,
у.
Каж
дой
паре
(действительных)
чи
сел
х,
у
соответствует
точка
М.
42

ВЗАИМНО
ОБРАТНЫЕ
ФУНКЦИИ
Две
функции
f
и
9
называются
взаимно
обратными,
если
формулы
у
=
f(x)
и
х
=9
(у)
выражают
одну
и ту
же
зависимость
между
переменны
ми
х
и
у:
y=f(x)~x=g(y).
у
5
у=2х+5
и
Х=--
2 2
у=х3;
х
~ О
и
х
=
~
у
=1
ОХ;
и
х
=Ig
У
Поскольку
принято
аргумент
функции
обозначать
переменной
х,
а
значение
функции
-
переменной
у,
то
обратную
функцию
для
функции
у
=
f(x)
записывают
в
виде
у
=
g(x).
Функция
Обратная
функция
у
= log2
Х
У
=
2
Х
у
=
х
2
;
Х
~ О
у=Б
. [ n
n]
У=SIПХ;
хЕ
-2;
2
у
=
агсsiпх
у
=
cos
х;
х
Е
[О;
n]
у =
arccosx
.
(n.
n )
у
=
tg
х,
х
Е
-
2'
2
у
=
arctgx
у
=
ctgx;
х
Е
(О;
n)
у
=
arcctgx
Функция
имеет
обратную,
если
функция
строго
воз
растает
ил
и
строго
убы
вает(строго
монотонная
функция}.
Чтобы
получить
обратную
функцию
от
некоторых
функций,
уменьшают
об
ласть
определения
функ
ции
так,
чтобы
область
значений
функции
не
из
менилась.
Графики
функции
у
=
f(x}
и
обратной
функции
у
=
g(x}
(--j
симметричны
относитель
но
биссектрисы
угла
хОу
(прямая
у
=
х).
х
43
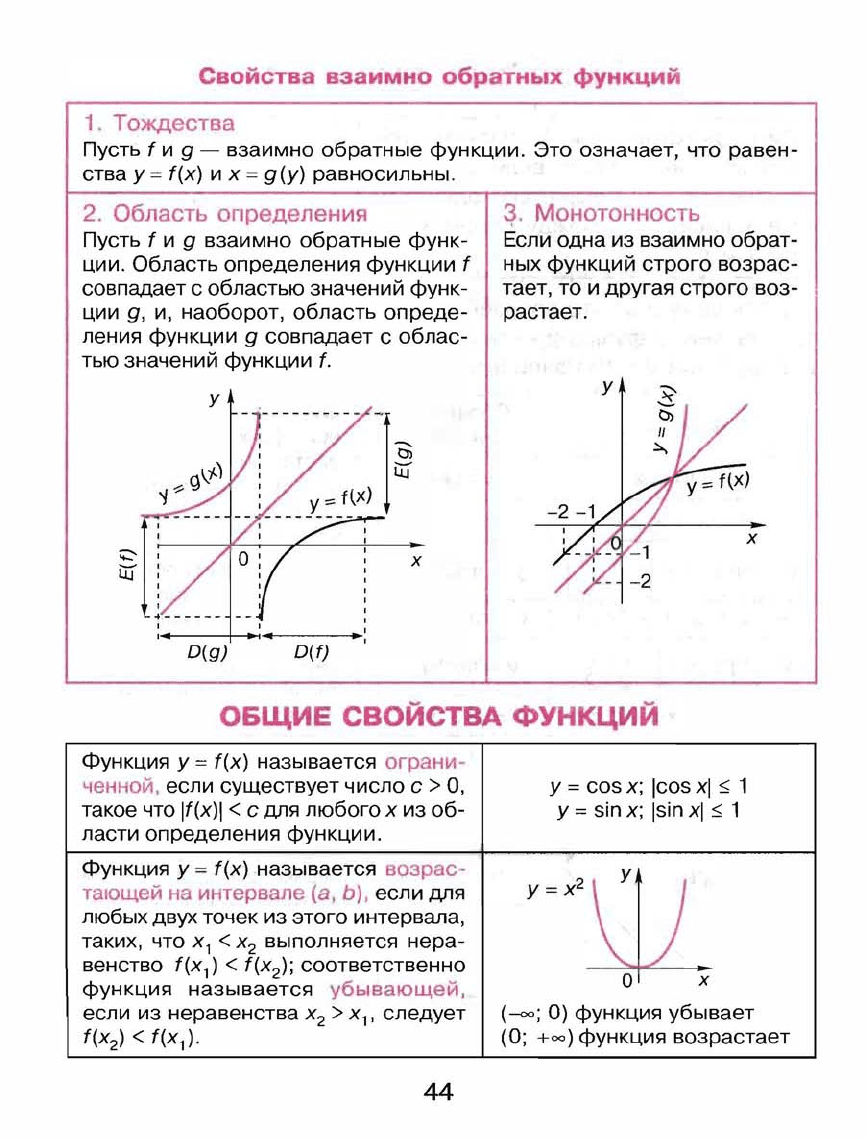
Свойства
взаимно обратных
функци
1.
Тождества
Пусть
f
и
9 -
взаимно
обратные
функции.
Это
означает,
что
равен
ства
у
=
'(х)
их
=
g(y)
равносильны.
2.
Область
определения
Пусть
f
и
9
взаимно
обратные
функ
ции.
Область
определения
функции
f
совпадает
с
областью
значений
функ
ции
g,
и,
наоборот,
область
опреде
ления
функции
9
совпадает
с
облас
тью
значений
функции
'.
З.
Монотонность
Если
одна
из
взаимно
обрат
ных
функций
строго
возрас
тает,
то
и
другая
строго
воз
растает.
ОБЩИЕ
СВОЙСТВА
ФУН
ЦИЙ
Функция
у
=
'(х)
называется
ограни
ченной.
если
существует число
с
>
О,
У
=
cos
х;
Icos
xl
s 1
такое
что
If(x)1
<
с
для
любого
х
из
об
у
= sin
х;
Isin
xl
s 1
ласти
определения
функции.
I
,
Функция
у
=
'(х)
называется
воэрас
тающей
на
интервале
(а,
Ь),
если
для
любых
двух
точек
из
этого
интервала,
таких,
что
Х
<
Х
2
выполняется
нера
1
венство
'(х
)
<
'(х
2
);
соответственно
1
функция
называется
убывающей,
если
из
неравенства
Х
2
>
х
1
,
следует
'(х
2
)
<
'(х
)·
1
У=Х'(
)
О
х
(-00;
О)
функция убывает
(О;
+00)
функция
возрастает
44

Функция
у
=
f(x)
называется
чет
ной,
если для
любого
х
из
обла
сти
определения
функции
вы
полняется
равенство:
I
f(-x)
=
f(x)
I
График
четной
функции
сим
метричен
относительно оси
Оу.
Четные
функции:
у =
COSX,
т.
к.
cos
(-х)
=
cosx;
у
=
х
2
,
т.
к.
(-х)2
=
х
2
Функция
у
=
f(x)
называется
не
четной,
если
для
любого
х
из
области
определения
функции
выполняется
равенство:
If(
-х)
=
-f(x)
I
График
нечетной
функции
сим
метричен
относительно
начала
координат.
Нечетные
функции:
у
=
х3,
т.
к.
(-х)З
=
-х3;
у
=
sinx,
т.
к.
sin
(-х)
=
-sin
х;
у
=
tgx,
т. к.
tg
(-х)
=
-tgx;
У
=
ctgx,
т.
к.
ctg
(-х)
=
-ctg
х
Функция
у
=
f(x)
называется
пе
риодической,
если
существует
такое
число
Т"*
О,
что
для
любо
го
значения
х
из
области
опре
деления
функции,
числа
(х
+
т)
и
(х
-
т)
также
входят
в
область
определения
и
при
этом
выпол
няется
равенство:
If(X
+
т)
=
f(x)
I
Главным
периодом
(или
просто
периодом)
принято
называть
наи
меньшее
положительное
число
Т,
являющееся
периодом
функ
ции.
Периодические
функции:
у
=
sinx,
Т
=
271:;
У
=
cosx,
Т
=
271:;
У
=
tg
х,
Т
=
71:;
У
=
ctg
х,
Т
=
71:,
т.
к.
соответственно:
sin
(х
+
271:k)
= sin
х;
cos
(х
+
271:k)
=
cos
х;
tg
(х
+
7I:k)
=
tgx;
ctg
(х
+
7I:k)
=
ctg
х,
где
k =
О,
±1, ±2, ...
45

ЛИНЕЙНASI
функция
и
ЕЕ
ГРАФИК
Линейной
функцией
назыаетсяя
функция
у
=
kx
+
Ь,
где
k
и
Ь
-
некоторые
числа.
Прямопропорциональная
зависимость
между
переменными
х
и
у:
при
водит
к
простейшей
линейной
функции
у
= kx.
Свойства
линейной
функции
у
=
kx
при
k
~
О
1.
Область
определения
функции
-
у
множество
R
всех
действительных
3
чисел.
2.
Корни
-
единственный
корень
х
=
О.
З.
Промежутки
постоянного
знака
зави
сят
от
знака
параметра
k:
а)
k >
О,
то
у
>
о
при
х
>
О;
У
<
О
при
х
<
О;
б)
k <
О,
то
у
>
О
при
х
<
О;
х
У
<
О
при
х
>
О.
4.
Экстремумов
нет.
5.
Монотонность
функции:
если
k>
О,
то
у
числовой
оси;
если
k <
О,
то
у
убывает
на
всей
числовой
оси.
6.
Наибольших
и
наименьших
значений
нет.
7.
Область
значений
-
множество
R.
8.
Четность
-
функция
у
=
kx
нечетна.
возрастает
на
всей
Графиком
линейной
функции
у
=
kx
является
прямая,
проходящая
через
начало
координат.
Коэффициент
k
называется
угловым
коэф
фициентом
этой
прямой.
ОН
равен
тангенсу
угла
наклона
этой
пря
мой
к
оси
х:
k =
tg
0:.
При
положительных
k
этот угол
острый,
при
от
рицательных
-
тупой.
График
линейной
функции
у
=
kx
+
Ь
есть
прямая.
Для
построения
графика
достаточно
двух
точек.
Например:
А(О;
Ь)
и
В(
-
~;
О
).
если
k::l:-
О.
46
Типовые
задания
1.
а)
Постройте
график
функции
у
у
=
-2,5х.
б)
Возрастающей
или
убываю
I 1
х
щей
является
эта
функция?
а)
Графиком
функции
является
пря
I
I
мая,
проходящая
через
начало
I
,
1
координат
I
поэтому
достаточно
_2'51-----·1
взять
еще
одну
точку
(1;
-2,5).
б)
k =
-2,5;
k <
О
-
функция
у
=
-2,5х
является
убывающей.
2.
а)
Постройте
график
функции
у
=
2х
-
З.
б)
При
каком
значении
х
значе
ние у
равно
-5?
в)
Укажите
значения
х,
при
кото
рых
у
<
О.
г)
Укажите
значения
х,
при
кото
рых
у>
О.
д)
Укажите
координаты
точек
пе
ресечения
графика
с
осями
координат.
а)
Графиком
функции
является
прямая.
Для
построения
рас
считаем
две
точки
прямой,
расположенные
на
осях
Ох
и Оу:
на
оси
Оу:
пусть
х
=
О,
У
= 2 .
0-3
=
-3;
(.)А(О;
-3);
на
оси
Ох:
пусть
у
=
О,
0=
2х
-
З.
2х
= 3,
х
=1,5; (.)
8(1
,5;
О).
б)
При
х
=
-1
значение
у
=
-5
(по
графику
точка
С).
в)
у
<
О
при
х
Е
(-00; 1,5) -
график
функции
лежит
ниже
оси
Ох.
г)
у>
О
при
Х
Е
(1,5;
+00)
-
график
функции
лежит
выше
оси
Ох.
д)
На
оси
Ох
точка
8(1 ;5;
О),
на
оси
Оу
точка
А(О;
-3).
47
\\
I
I
~:
-t5\ '
-,<.'
х
КВАДРАТИЧНASI
функция
и
ЕЕ
ГРАФИК
ФУНКЦИЯ,
заданная
формулой
у=ах
2
+ьх+с,
где
х
и
у
переменные,
а
а,
Ь,
с
-
заданные
числа,
причем
а"*
О,
на
зывается
квадратичной
функцией.
Если
а
=
1,
Ь
=
с
=
О,
то
квадратичная
ФУНКЦИЯ
у=х
2
.
Свойства
квадратичной
функции
Функция
у=х
2
у==ах
2
+Ьх+с
1.
Область
опреде
множество
R
множество
R
ления
функции
Ь.
Ь
2
-4ас
2.
Координаты
вер
(О;
О)
(Ха;
Уа)
Ха
==
-
2а'
Уа
::-
шины
параболы
4а
Х
=
_!l.-
+ .Jb
2
-
4ас
1,2
2а
-
2а
З.
Корни
функции
х=о
(нули
функции)
при
Ь
2
-
4ас
~
О;
нет
корней при
Ь
2
-
4ас
<
О
минимум
минимум
в
вершине,
если
а
>
О
4.
Экстремумы
в
вершине
максимум
в
вершине,
если
а
<
О
функции
5.
Область
значе
[Уа;
+00),
если
а
>
О
[О;
+00]
ний
(-00;
Уа]'
если
а
<
О
четная
ни
четная,
ни
нечетная
6.
Четность
График
квадратичной
функции
-
парабола.
Если
а
>
О,
то
ветви
параболы
направлены
вверх.
Если
а
<
О,
то
ветви
параболы
направлены
вниз.
.J,.
-!r
у у
CJ
-1
О
1 2
х
(-00;
О)
функция
убывает.
(О;
+00)
функция
возрастает.
48
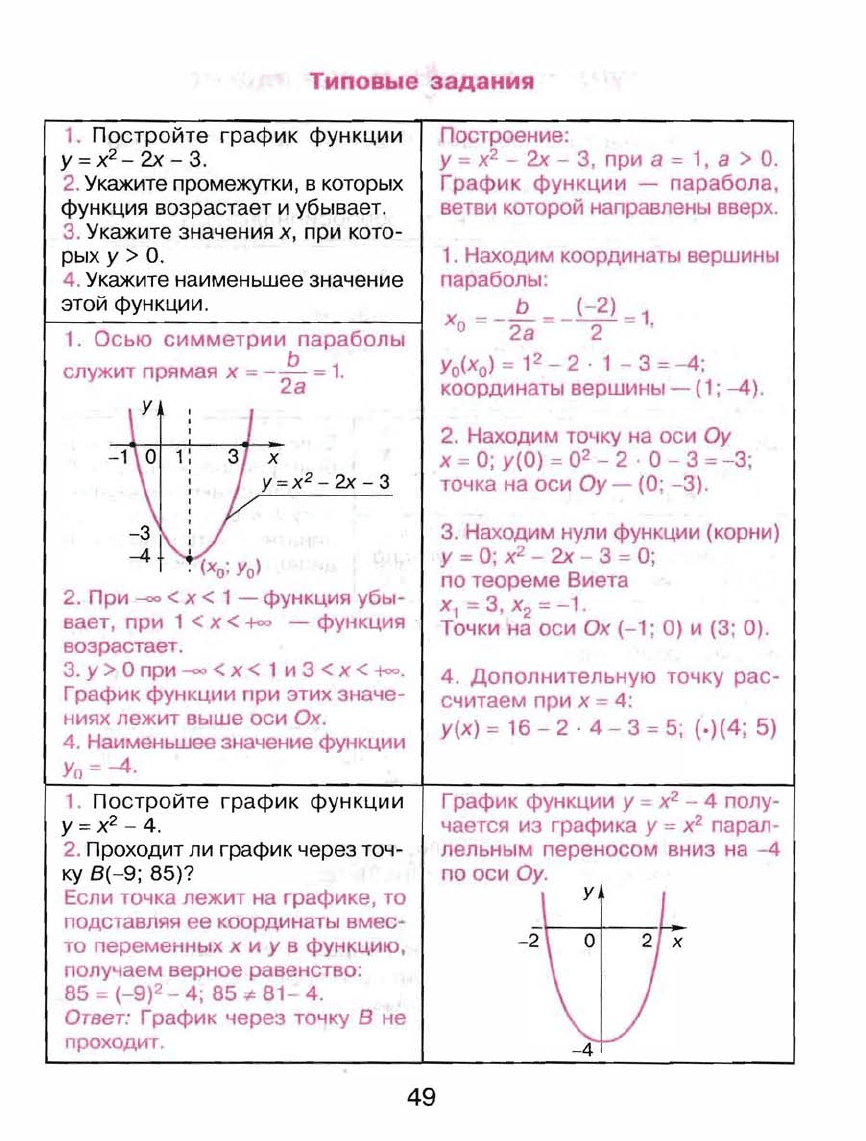
Типовые
задания
1.
Постройте
график
функции
у:::::
х
2
-
2х
- 3.
2.
Укажите
промежутки,
в
которых
функция
возрастает
и
убывает.
3.
Укажите
значения
Х,
при
кото
рых
у>
О.
4.
Укажите
наименьшее
значение
этой
функции.
3.
Находим
нули
функции
(корни)
у
:::::
О;
х
2
-
2х
- 3
:::::
О;
по
теореме
Виета
X
1
:::::
3.
х
2
:::::-1
Точки
на
оси
Ох
(-1;
О)
и
(3;
О).
4.
Дополнительную
точку
рас
считаем
при
х
=4:
у(х}:::::16-2·4-3=5;
(.)(4; 5)
2.
Находим
точку
на
оси
Оу
х
=
О;
у(О)
:::::
02 - 2
О
- 3
:::::
-3'
точка
на
оси
Оу-
(О;
-3).
Построение:
у
:::::
х
2
-
2х
- 3,
при
а
:::::
1,
а
>
О.
ГрафИк
функции
-
парабола.
ветви
которой
направлены
вверх.
1.
Находим
координаты
вершины
параболы:
Ь
(-2).
Ха
:::::
--
:::::
---
= 1
2а
2 •
Уо(Х
о
)
:::::
12 - 2 . 1 - 3 :::::-4;
координаты
вершины
-
(1;
-4).
х
у=х
2
-
2х
- 3
-1
1.
Осью
симметрии
параболы
служит
прямая
Х
:::::
-
2
Ь
а
:::::
1.
у
,
(Ха;
уо)
2.
При
---<>о
<
Х
< 1 -
функция
убы
вает,
при
1 <
Х
<
-t<:o
-
функция
возрастает.
3.
У
>
О
при
---о<>
<
х
< 1
и
3 <
Х
<
-J-<><>.
График
функции
при
этих значе
ниях
лежит
выше
оси
Ох.
4.
Наименьшее
значение
функции
Уа:::::
-4.
1.
Постройте
график
функции
у:::::
х
2
-
4.
2.
Проходит
ли
график
через
точ
ку
8(-9;
85)?
Если
точка
лежит
на
графике,
то
подставляя ее
координаты
вмес
то
переменных
х
и
у
в
функцию.
получаем
верное
равенство:
85:::::
(-9}2
-
4;
85
~
81-
4.
Ответ:
График
через
точку
В
не
проходит.
График
функции
у
:::::
х
2
- 4
полу
чается
из
графика
у:::::
х
2
парал
лельным
переносом
вниз
на
-4
по
оси
ау.
-4
49

ФУНКЦИЯ
у
=
~
И
ЕЕ
ГРАФИК
х
Переменные
х
и
у
связаны
обратно
пропорциональной
за
висимостью
у
=
~
J
где
k
*-
О.
k -
коэффициент
обратной
пропорциональности.
У
Графиком
обратной
пропорциональности
11
У
=!i
является
кривая,
состоящая
из
х
~
х
двух
ветвей,
симметричных
относительно
~
IV
начала
координат.
Это
гипербола.
k
Область
определения
функции
У
= -
Если
k >
О,
то
ветви
гипер
х
болы
расположены
в
1
и
111
есть
множество
всех
чисел,
отличных
от
координатных
четвертях,
нуля,
т.
е.
(-00;
O)u(O;
+00).
если
k <
О,
то
11
и
IV
коор
Гипербола
не
имеет
общих
точек
с
ося
динатных
четвертях
коор
ми
координат,
а
лишь
сколь
угодно
динатной
плоскости.
близко
к
ним
приближается,
т.
к.
Х
*-
О.
Пример.
Решите
графически
систему
уравнений:
4
у
{
у
=
;,5Х
2
4~1234
Решение.
1.
у
=-
Х
у
4 2
4/3
1
График
функции
-
гипербола,
k = 4, k >
О,
ветви
гиперболы
расположены
в
1
и
111
координатных
четвертях.
2.
у
=
0,5х
2
График
функции
-
парабола
а
= 0,5,
а
>
О,
ветви
параболы
направлены
вверх.
~
Графики
функций
пересекаются
в
одной
У
10
1o,51214,518
точке,
система
имеет
одно
решение
Х
=
2;
у
=
2.
х
У=
О,5х
2
./" 4
У=
х
х=2
Ответ:
(2; 2).
50
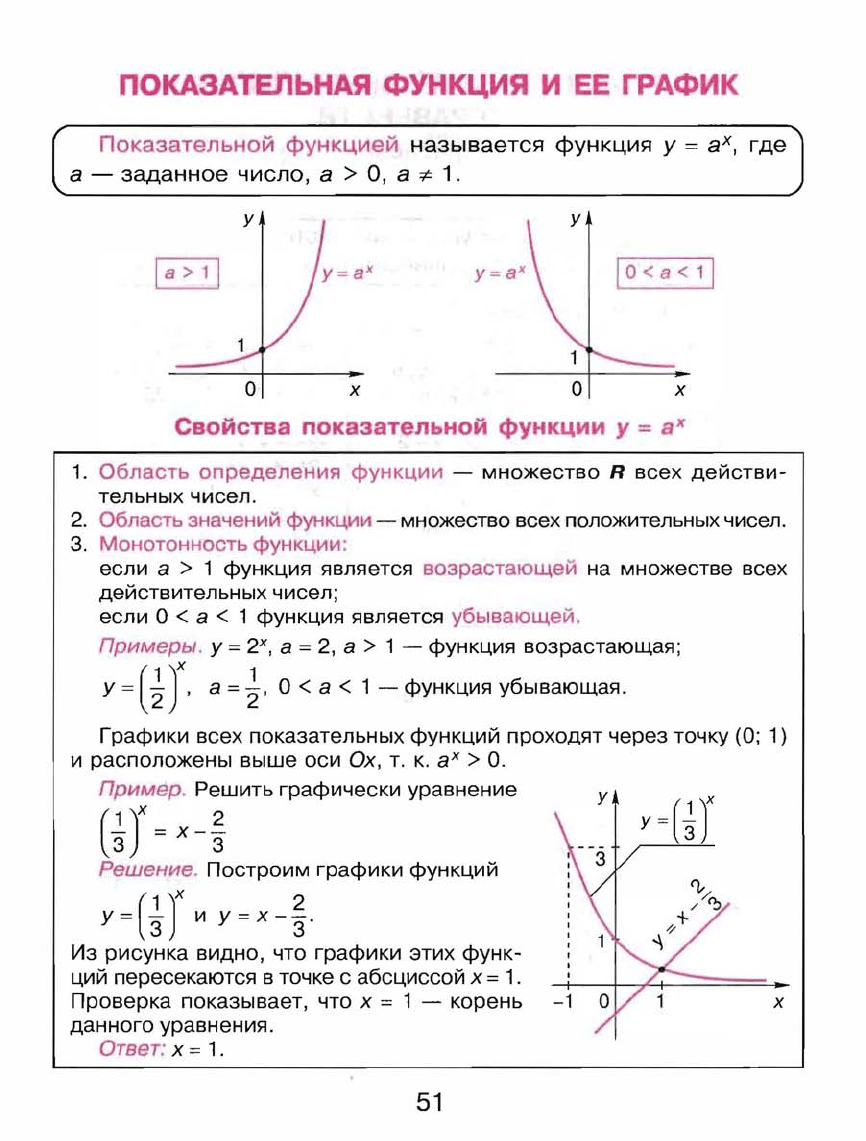
ПОКАЗАtЕЛЬНАЯ
функция
и
ЕЕ
ГРАФИК
Показательной
функцией
называется
функция
у
=
аХ,
где]
а
-
заданное
число,
а
>
О,
а*-1.
в
х
у;
аХ
у
х
lo<a<11
Свойства
показательной
функции
у
=
аХ
1.
Область
определения
функции
-
множество
R
всех
действи
тельных
чисел.
2.
Область
значений
функции
-
множество
всех
положительных
чисел.
З.
Монотонность
функции:
если
а
> 1
функция
является
возрастающей
на
множестве
всех
действительных
чисел;
если
О
<
а
< 1
функция
является
убывающей.
Примерbl.
у
=
2
Х
,
а
=
2,
а
> 1 -
функция
возрастающая;
1
)Х
1
У
=
"2
'
а
= 2'
о
<
а
< 1 -
функция
убывающая.
(
Графики
всех
показательных
функций
проходят
через
точку
(О;
1)
и
расположены
выше
оси
Ох,
т.
к.
аХ
>
О.
Пример.
Решить
графически
уравнение
у
у
=(~J
(~J
=
x-~
Решение.
Построим
графики
функций
у
=(
~)X
И
у
=
х
_
~.
Из
рисунка
видно,
что
графики
этих
функ
ций
пересекаются
в
точке
с
абсциссой
х
=
1.
Проверка
показывает,
что
х
= 1 -
корень
-1
х
данного
уравнения.
Ответ:
х
= 1.
51
