Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1

Подождите немного. Документ загружается.

5. Для проверки правильности расчета составляем баланс мощ-

ностей, предварительно определив напряжение на зажимах источника

тока. Он подключен между узлами b и d, поэтому

18 14 4 B.

Jbd





Все результаты совпали с полученными выше и уже проверенными

составлением баланса мощностей.

Методы контурных токов и узловых потенциалов позволяют со-

ставлять и решать системы с меньшим количеством уравнений, чем по

законам Кирхгофа. При этом первый метод удобнее применять, когда

число независимых контуров меньше числа узлов, а второй – когда чис-

ло

узлов не превышает числа независимых контуров.

3.5. Эквивалентные преобразования схем

Эквивалентными называются такие преобразования схем, при ко-

торых остаются неизменными токи и напряжения в части схемы, не за-

тронутой преобразованием.

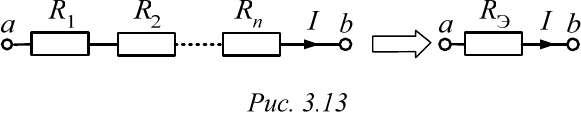
3.5.1. Последовательное соединение двухполюсников

Последовательным называется такое соединение двухполюсников,

при котором по всем двухполюсникам протекает один и тот же ток

(рис. 3.13).

По второму закону Кирхгофа

ab k k

URIIRRI







Здесь





то есть эквивалентное сопротивление ветви

равно сумме сопротивлений, включенных последовательно.

Частный случай: при

12 n

RRR



 

окажется

nR

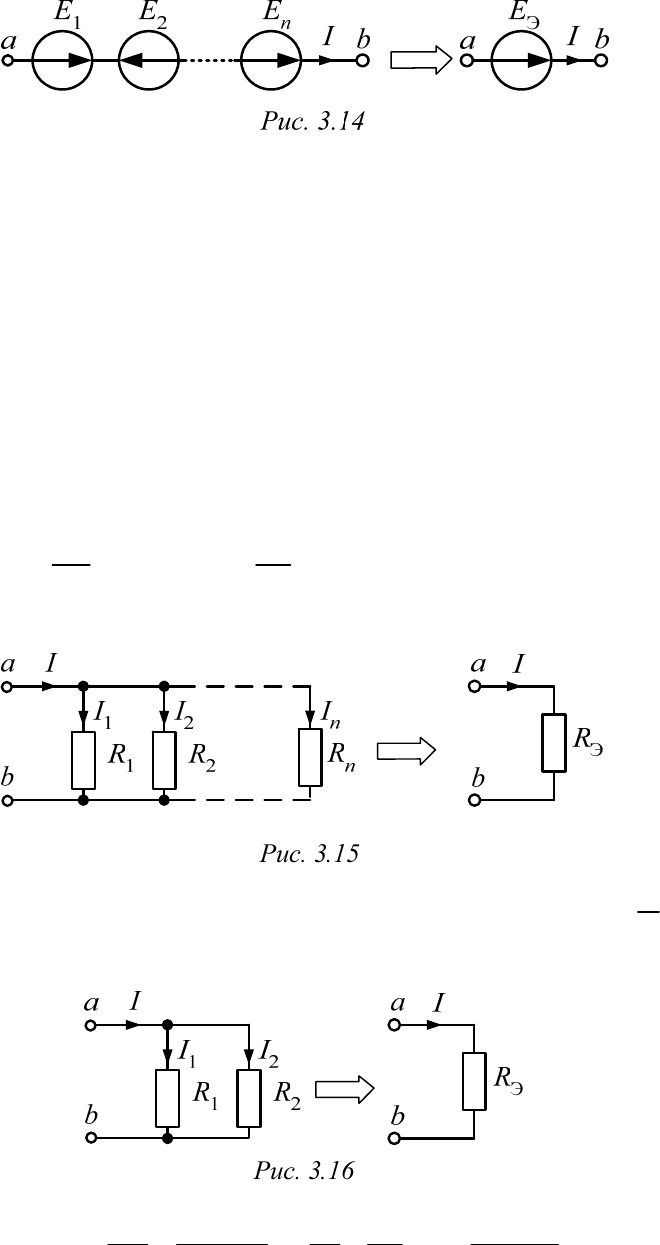
Для схемы рис. 3.14 по второму закону Кирхгофа имеем:

12 Э

... .

nba ab

EEUUE  

Значит, эквивалентная ЭДС равна

алгебраической сумме ЭДС источников, включенных последовательно.

Cо знаком «плюс» в этой сумме учитываются те из них, чьи стрелки

направлены по отношению к узлам так же, как стрелка

Последовательное соединение идеальных источников тока с раз-

ными задающими токами не имеет физического смысла.

3.5.2. Параллельное соединение двухполюсников

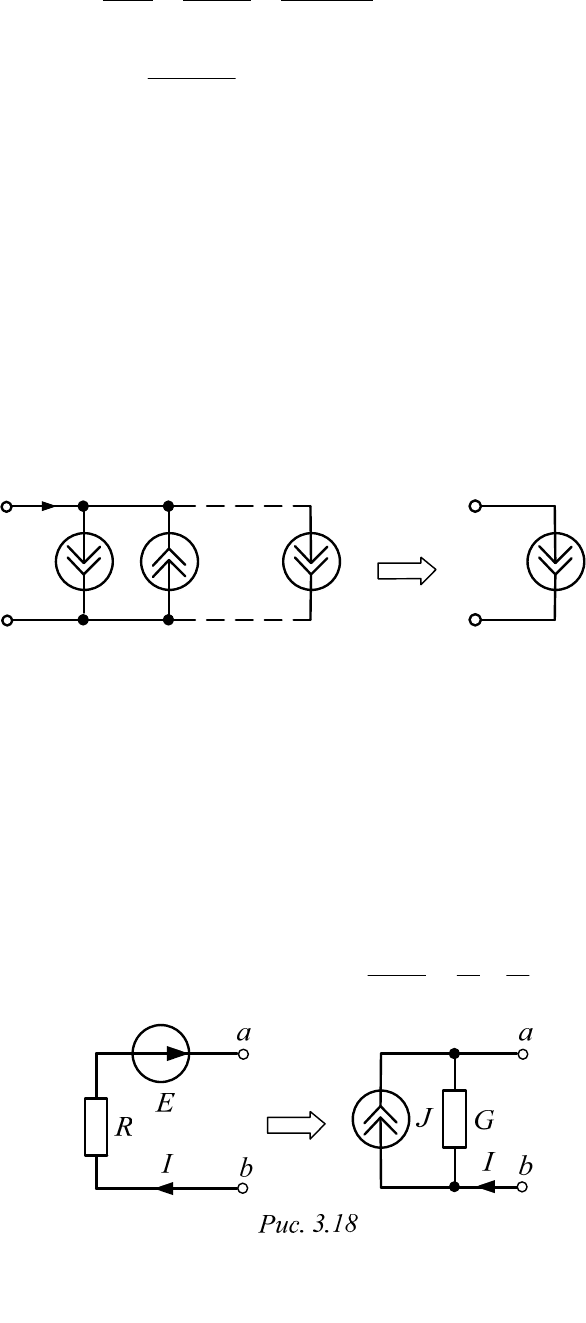
Параллельным называется такое соединение двухполюсников, при

котором все они находятся под одним и тем же напряжением (иными

словами, каждый из них подключен к одной и той же паре узлов, как на

рис. 3.15).

По первому закону Кирхгофа

111

GUGUGUII

kab







Отсюда



 



Значит, эквивалентная проводи-

мость равна сумме проводимостей параллельных ветвей.

Частный случай: при

RRRR



...

окажется



Еще один частный случай (схема рис. 3.16):

Э 12 1 2 12

11 11

GGG RR RR







  







Здесь же











По аналогии







Ток в одной из двух параллельных пассивных ветвей равен произве-

дению тока в неразветвленной части на сопротивление другой ветви,

отнесенному к сумме сопротивлений обеих ветвей (

правило парал-

лельных ветвей

Для схемы рис. 3.17 имеем

... 0,

IJ J J





но

JI 

по-

этому

Э 12

... .

JJ J

Задающий ток эквивалентного источника равен алгебраической

сумме задающих токов источников, включенных параллельно. Со зна-

ком «плюс» учитываются те из них, чьи стрелки направлены по отно-

шению к узлам так же, как стрелка эквивалентного источника

Параллельное соединение источников напряжения с различными

ЭДС не имеет физического смысла.

3.5.3. Эквивалентное преобразование последовательного

соединения Е и R в параллельное соединение J и G

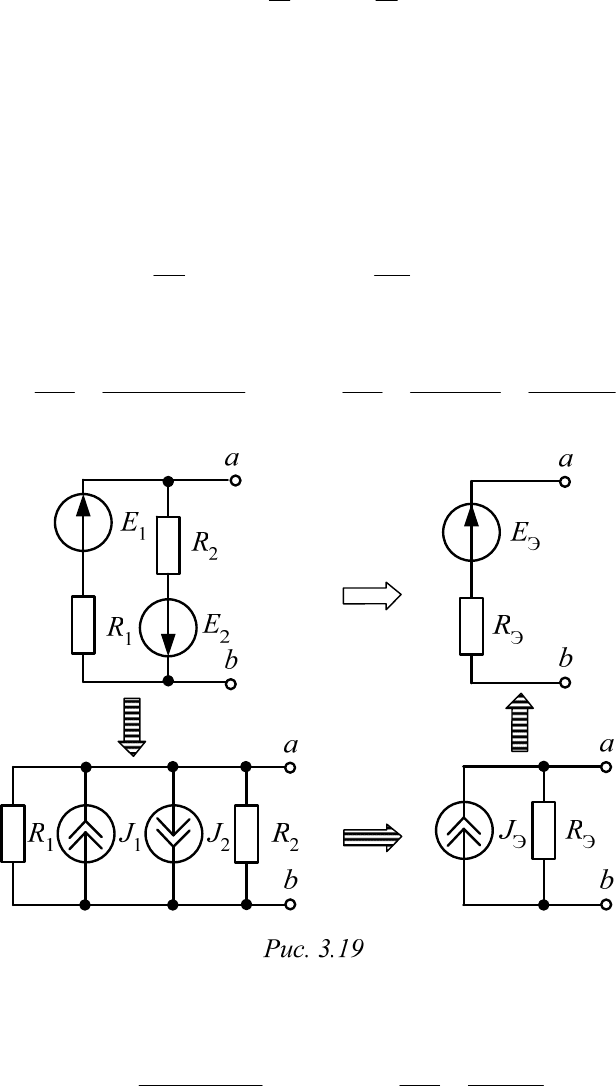
По второму закону Кирхгофа для схемы с последовательным со-

единением и по первому закону для схемы с параллельным соединени-

ем

(рис. 3.18) можно записать:

URIEU

abab







Рис. 3.17

Эти выражения тождественны лишь при равенстве слагаемых как

не зависящих от тока I, так и пропорциональных ему. Поэтому

В обеих схемах сопротивление одинаково, а ЭДС и задающий ток

источников связаны законом Ома.

3.5.4. Параллельное соединение активных ветвей

Воспользовавшись уже известными преобразованиями (переход от

одной схемы к другой на рис. 3.19 по стрелкам), найдем:

1112 22

;;

EG J E G

  

12 Э 12

;;

JJ G GG 

12 21 1 2

ЭЭ

Э 12 Э 12 12

тогда ;.

RER RR

GRR GGGRR



  



В общем случае n параллельных ветвей

ЭЭ













G 

В числителе предпоследней формулы сумма алгебраическая: со

знаком «плюс» записываются ЭДС тех источников, чьи стрелки направ-

лены по отношению к узлам так же, как и

, со знаком «минус» –

направленные в противоположную сторону.

3.5.5. Перенос источника ЭДС через узел (рис. 3.20)

Пусть





тогда в исходной схеме

234









Включим в

каждую из ветвей одинаковые по величине ЭДС Е, направленные от уз-

ла 4. При этом потенциалы узлов 2 и 3 не изменятся. В первой ветви две

ЭДС скомпенсируют действие друг друга и их можно удалить.

В эквивалентной схеме

14 23

0 и ,









т. е. изменился

лишь потенциал узла 4, а ЭДС оказалась «вытесненной» из одной ветви

во все остальные. Это преобразование удобно применять, когда в схеме

есть активная ветвь без сопротивления. После него эта («особая») ветвь

может быть устранена вместе с одним из узлов.

3.5.6. Перенос источника тока в контуре

В схеме рис. 3.21, а выделены две ветви с сопротивлениями

, образующие с источником тока замкнутый контур. Включим после-

довательно с одним источником тока еще один такой же и подключим

точку их соединения к узлу 3 (рис. 3.21, б). При этом мы не нарушили

первый закон Кирхгофа и не изменили режим работы остальной части

цепи

(0).I 

Заменим параллельное соединение источников тока J с пассивной и

активной ветвями последовательным соединением источников ЭДС с

теми же сопротивлениями. Получим схему рис. 3.21, в, в которой дей-

ствуют новые ЭДС

RJ

ERJ





. По сравнению с исходной

схемой удалось избавиться от одного («особого») контура. Токи в со-

противлениях этого контура после преобразования изменятся, а в

остальной части схемы сохранят прежние значения.

Это преобразование легко распространить на любое число ветвей,

образующих контур с источником тока.

3.5.7. Преобразование треугольника в звезду и обратно

Для треугольника (рис. 3.22) по законам Ома и Кирхгофа имеем:

31 12 1 23 2 12

;;IIIIII 

)(

312312

31123231312323312312

RRU

RIRIRIRIUUU





12 31 23 12

12 1 2 12 23 31

откуда , где .

RR RR

UI I RRRR







 

Но для звезды

12 1 1 2 2

.UIRIR 

Коэффициенты при одних и тех же токах должны быть равны, по-

этому

12 31 23 12

RRR







По аналогии

31 23







Сопротивление луча звезды, подключенного к данному узлу, равно

произведению сопротивлений сторон треугольника, подключенных к

тому же узлу, отнесенному к сумме сопротивлений всех его сторон.

Если подсчитать







RRR

RRRRRR

312312

133221

и разделить

этот результат на каждое из сопротивлений лучей звезды, то получим:

23 31

12 1 2 23 2 3 31 3 1

312

;;.

RRR

RRR RRR RRR

RRR



    

Сопротивление стороны треугольника, включенной между данными

узлами, равно сумме сопротивлений лучей звезды, подключенных к тем же

узлам, и их произведения, отнесенного к сопротивлению третьего луча.

Если в одной из ветвей треугольника есть источник ЭДС

(рис. 3.23), то в лучах эквивалентной звезды, подключенных к тем же

узлам, что и активная ветвь треугольника, появляются две ЭДС, про-

порциональные их сопротивлениям:

23 2 23 3 23

2 2 23 3 3 23 23

23 23 23

,,где ,

ER ER E

ERJ ERJ J

RRR



    

что легко доказывается с помощью уже известных

преобразований.

Сопротивления лучей эквивалентной звезды вычисляются так же, как и

в случае с пассивными звездой и треугольником.

Направление стрелок, эквивалентных ЭДС, по отношению к узлам

такое же, как и у ЭДС в ветвях треугольника.

Варианты с несколькими ЭДС сводятся к рассмотренному посред-

ством переноса ЭДС через узел. Преобразование активной звезды в тре-

угольник трудностей не представляет.

3.6. Некоторые свойства линейных электрических цепей

3.6.1. Принцип наложения

Ток в любой ветви сложной цепи с несколькими источниками

можно рассматривать как сумму составляющих от действия каждого

источника тока или напряжения в отдельности.

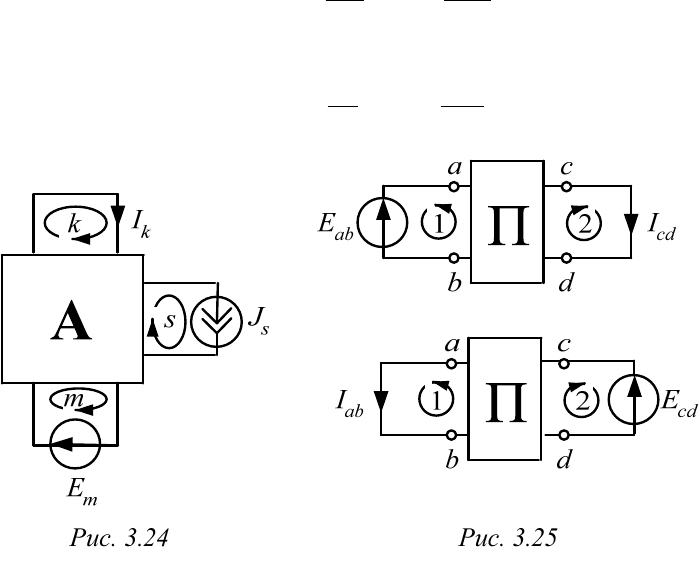
Докажем это положение, определив методом контурных токов ток

в k-й ветви схемы рис. 3.24.













sks

mkm

JHEGJI

(3.9)

Здесь  – главный определитель системы независимых уравнений с

контурными токами,



– определитель, который получается из  заменой

k-го столбца правыми частями этих уравнений. Если расписать



по мино-

рам этого столбца, то получится полином. Коэффициенты при ЭДС и зада-

ющих токах источников представлены нижеследующими обозначениями.

G 

взаимная (передаточная) проводимость ветвей k и m, чис-

ленно равная току в k-й ветви от действия источника напряжения с ЭДС

в 1 В, включенного в m-ю ветвь при отсутствии других источников, ко-

торые заменяются внутренними сопротивлениями. Иными словами, ес-

ли



то источник ЭДС следует заменить короткозамкнутым про-

водником; если

0,J 

то ветвь с источником тока нужно отключить.

G 

входная проводимость схемы относительно зажимов, обра-

зующихся при размыкании k-й ветви и отсутствии источников. Эта вели-

чина появляется в формуле в том случае, если ЭДС находится в ветви k.

H 

коэффициент передачи по току между ветвями k и s, чис-

ленно равный току в k-й ветви от источника с задающим током в 1 А,

включенного в ветвь s (опять же при отсутствии других источников).

3.6.2. Принцип взаимности

Ток

II

в ветви cd от действия источника ЭДС

E

, вклю-

ченного в ветвь ab при отсутствии других источников, будет равен то-

ку

II

в ветви ab, если в ветвь cd переместить ту же ЭДС

E

Вновь воспользуемся методом контурных токов для расчета обеих

схем рис. 3.25. Выберем независимые контуры таким образом, чтобы

контурный ток

оказался единственным, который замыкается в вет-

ви ab, а

– единственным, замыкающимся по ветви cd.

Тогда в верхней схеме рис. 3.25

а в нижней

Здесь  – главный определитель системы уравнений с контурными

токами (он одинаков для обеих схем, так как составляется только из со-

противлений),

12 21

и

его алгебраические дополнения.

Определитель  симметричен относительно главной диагонали, по-

скольку общие сопротивления контуров равны

km mk



Поэтому

12 21

,

и, следовательно,

cd ab

III



Теорема доказана.

3.6.3. Принцип (теорема) компенсации

Ток в любой ветви не изменится, если ее сопротивление заменить

источником напряжения с ЭДС, равной напряжению на зажимах этого

сопротивления и имеющей ту же полярность, или источником тока, чей

задающий ток равен току в этой ветви и имеет то же направление.

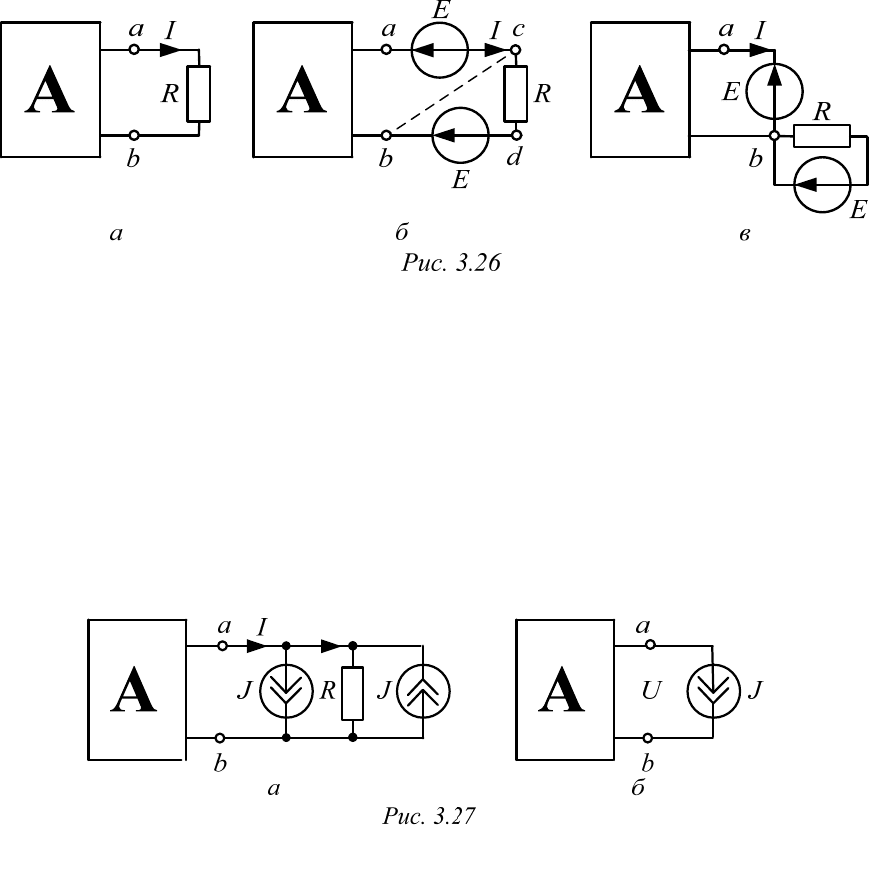
Докажем это положение на примере схемы рис. 3.26, а.

Токи в

ветвях схемы не изменятся, если последовательно с сопро-

тивлением R включить два одинаковых источника ЭДС Е противопо-

ложной полярности (рис. 3.26, б).

122











 EJI

211











 EJI

Принимая потенциал точки b равным нулю, найдем







 

URI





Если



то





и эти точки можно

сначала соединить проводником (пунктир на рис. 3.26, б), затем совме-

стить, а потом и отделить образовавшийся контур от остальной части

цепи. При этом потенциалы узлов а и b сохраняют свои значения, сле-

довательно, не меняются и токи в цепи. Но сопротивление R с током I

теперь заменено

источником ЭДС





(рис. 3.26, в).

Токи в цепи рис. 3.26, а также не изменятся, если параллельно со-

противлению включить два одинаковых источника тока J противопо-

ложного направления (рис. 3.27, а).

По первому закону Кирхгофа ток







При



этот ток ра-

вен нулю, поэтому проводник с током



можно оборвать (рис. 3.27, б).

После этого левая часть схемы выглядит так же, как исходная схема, но

вместо сопротивления с током I оказывается источник тока

JI того

же направления.

Теорема доказана. Заметим на будущее, что она справедлива и для

нелинейных цепей.

3.6.4. Теорема об эквивалентном генераторе

Любой активный двухполюсник можно заменить эквивалентным

генератором, параметры схемы замещения которого определяются

через параметры заменяемого двухполюсника.

