Epstein N., Grace J.R. Spouted and Spout-Fluid Beds: Fundamentals and Applications

Подождите немного. Документ загружается.

Empirical and analytical hydrodynamics 37

That would be even more likely when reliable values of both φ and ε

are available, so

and C

can be evaluated directly from Eq. (3.30) and (3.31), respectively (although the

Ergun equation also has ﬁnite conﬁdence limits). By the same token, equations for U

and U

that are better than Eqs. (3.28) and (3.32), respectively, for speciﬁc conditions

can be used to re-derive an equation for H

that would give greater quantitative accuracy

than Eq. (3.33) for those conditions, although qualitative trends of H

with process

variables would be similar.

From the deﬁnition of the Archimedes number, Ar,

= [μ

Ar/ρ(ρ

− ρ)g]

1/3

. (3.34)

Replacing d

by Eq. (3.34) into Eq. (3.33), differentiating the result by Ar and setting the

answer equal to zero generates a critical value of Ar = 223 000, at which H

is a max-

imum with respect to d

, at constant D, D

,μ,ρ,ρ

, and g.As

(

223 000

)

1/3

= 60.6,

)

crit

= 60.6[μ

/ρ(ρ

− ρ)g]

1/3

. (3.35)

Thus Eq. (3.33), unlike other empirical or theoretical equations

for H

, shows that

if the particles are small enough, H

increases rather than decreases with increasing

particle diameter, in agreement with experimental observations.

11,12,23

If column

dimensions and d

are kept constant and Ar is allowed to vary only by changing μ, ρ,

and ρ

− ρ, then Eq. (3.33) can be simpliﬁed to

= a[(1 + cAr)

1/2

− 1]

/Ar, (3.36)

where a = 568b

8/3

2/3

and c = 35.9 × 10

−6

. Differentiation of H

with respect

to Ar results in

(

)

(

2 + cAr

)

− 2

(

1 + cAr

)

1/2

]

(

1 + cAr

)

1/2

. (3.37)

Because

(

2 + cAr

)

> 2

(

1 + cAr

)

1/2

for positive c and Ar, dH

/dAr is always positive.

In the case of gas spouting, for which ρ

 ρ so that ρ

− ρ is almost invariant

with temperature, as the bed temperature rises, μ increases and ρ decreases, and thus

Ar decreases. Therefore, H

decreases with increasing temperature. This trend is

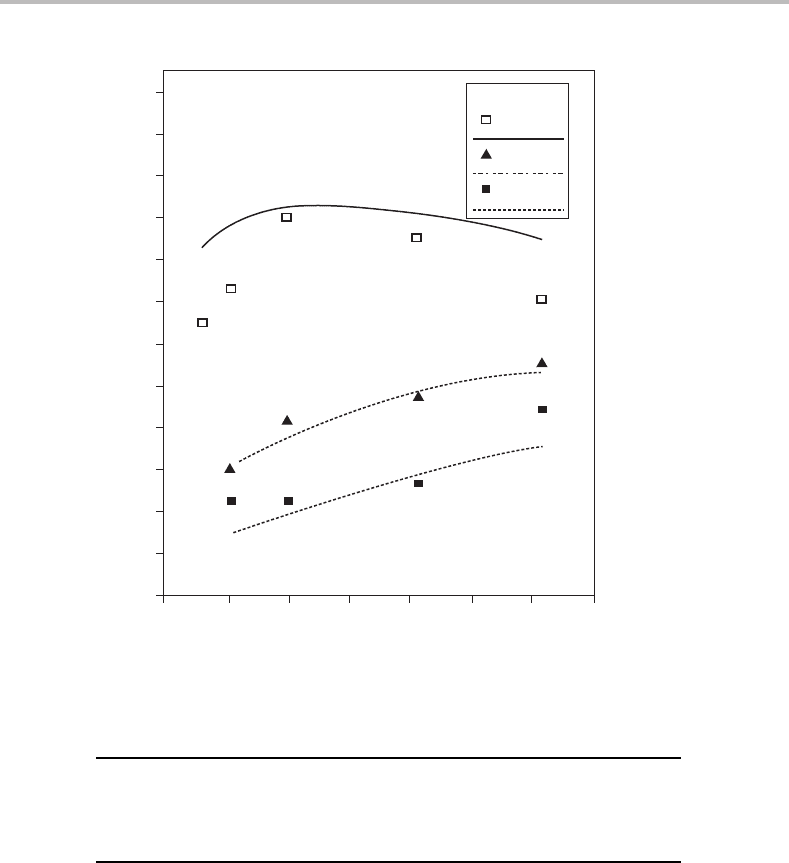
illustrated both experimentally and via Eq. (3.33) in Figure 3.1, which, along with its

accompanying table, also shows that (d

)

crit

increases with temperature as predicted by

Eq. (3.35), again because of increasing gas viscosity and decreasing gas density with

increasing temperature. Other conﬁrmatory data

by spouting with different gases

showed H

increasing as ρ increased at constant μ, and decreasing as μ increased

at constant ρ. In the case of gas spouting at elevated pressure, because gas viscosity

is only minimally affected by pressure, whereas gas density is nearly proportional to

the absolute pressure, one would expect Ar and hence H

to increase and (d

)

crit

decrease with increasing pressure. The effect of an increase in ρ

, and hence in Ar

for constant d

and constant gas properties, is to increase H

and decrease (d

)

crit

Eqs. (3.33) and (3.35), respectively, although the empirical equation of Malek and Lu

38 Norman Epstein

1.2

1.1

1.0

LEGEND

20 °C

300 °C

580 °C

0.9

0.8

0.7

Max. spoutable bed height, H

(m)

0.6

0.5

0.4

0.3

0.2

0.1

0.0

0.0 1.0 1.2

= 156 mm

= 19.06 mm

1.4 1.6 1.8 2.0 2.2

Particle diameter, d

(mm)

Figure 3.1. Effect of bed temperature and particle diameter on H

for air-spouting of closely

sized, nearly spherical sand particles in a conical-cylindrical column with a cone base diameter =

31 mm and included angle = 55

◦

. Points are experimental; lines are Equation (3.33) with

b = 1.11. (From Li et al.,

courtesy of Journal of the Serbian Chemical Society.)

Temperature,

◦

C 20 300 580

ρ, kg/m

1.205 0.616 0.414

μ, kg/m · s1.84 × 10

−5

3.00 × 10

−5

3.79 × 10

−5

)

crit

, mm, Eq. (3.36) 1.358 2.353 3.139

based on air spouting at ambient conditions shows a small contrary effect of ρ

on H

and no critical d

(with H

decreasing only with increasing d

There is experimental evidence, backed by conﬁr matory calculations,

that the second

spouting instability cited above – choking and consequent slugging of the spout owing

to its particle-conveying capacity being exceeded – comes into play for gas spouting of

relatively small particles

(e.g., d

≤ 1.3mm

), and even for larger particles at elevated

temperatures.

The critical diameter given by Eq. (3.35) again appears to represent,

at least approximately, the transition criterion between the annulus-ﬂuidization and the

spout-choking mechanisms.

For liquid spouted beds, H

is the maximum penetration depth of the spout for a deep

bed, as liquid spouting is characterized by the onset of ﬂuidization in the annulus at

Empirical and analytical hydrodynamics 39

z = H

, and by persistence of internal spouting to a depth of H

, even when H > H

For such cases, a spouted bed of height H

is then capped by a particulately ﬂuidized

bed of height H − H

The similarity between spouting and ver tical jet penetration

in ﬂuidized beds has been otherwise noted, albeit for operation with a gas.

Unlike gas

spouting, liquid spouting is characterized

23,27

by a decrease of H

as d

increases for

all d

It should be emphasized that Eq. (3.33) and all other equations for H

proposed in

the literature, are based on data for D < 0.5 m. There are no experimental data on H

nor are there reliable equations for H

, when D > 0.5 m. An order of magnitude can be

estimated by rederiving an equivalent of the McNab-Bridgwater

equation, substituting

for Eq. (3.28) the Fane-Mitchell

modiﬁcation of the Mathur-Gishler equation applied

at H = H

, U

= U

, namely

(

RHS of Eq. 3.28

)

× 2D. (3.38)

Solving Eqs. (3.27), (3.32), and (3.38) for H

by elimination of U

and U

, the result

(

RHS of Eq. 3.33

)

/4D

, (3.39)

with D in meters. An alternative crude estimate of H

for D ≥ 0.5 m can be made using

the aforementioned approximate formula of Lefroy and Davidson,

which, unlike other

equations for H

in the literature,

is not necessarily limited to D < 0.5 m – that is,

= 0.68D

4/3

1/3

. (3.40)

Applying those two equations to the example in Section 3.1 of 5-mm glass beads

spouted with ambient air, for D = 1 m and D

= 20d

= 0.1m,soD

/D = 0.1 < 0.35,

Eq. (3.39) with b = 1 yields H

= 4.29 m and Eq. (3.41) gives H

= 3.98 m. The close

agreement of the two values for this case is probably a sheer coincidence, but 4 m is

higher than the highest value of H (2.6mforD = 0.91 m) at which U

has been

reported,

and can tentatively be considered an approximate estimate of H

for D = 1

m and the other imposed conditions.

3.4 Annular ﬂuid ﬂow

3.4.1 Mechanistic modeling

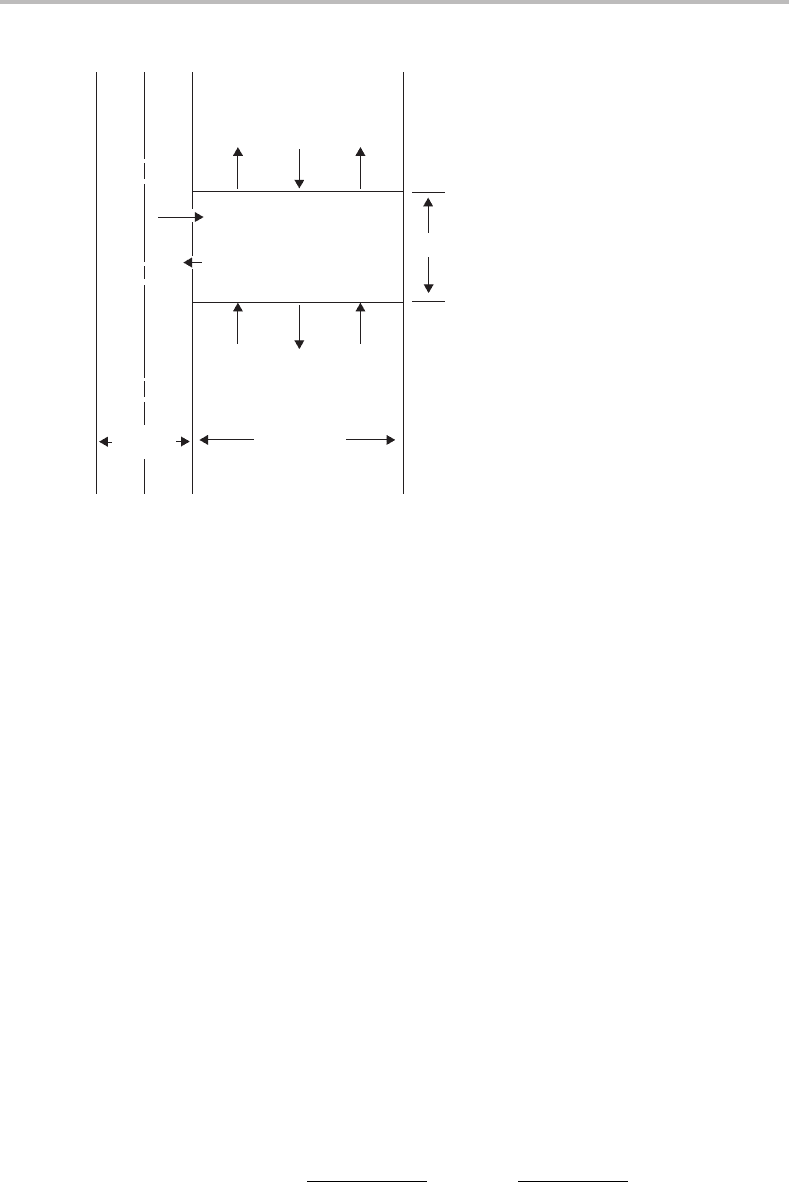
Consider the Mamuro-Hattori

model of the f orces acting in the annulus of a spouted

bed, illustrated by Figure 3.2. A vertical force balance on a differential height, dz,ofthe

annulus, neglecting friction at both vertical boundaries of the annulus, gives

−

(

+ dσ

)

= (ρ

− ρ)

(

1 − ε

)

gd z −

[

P −

(

P +dP

)

]

−dσ

= (ρ

− ρ)

(

1 − ε

)

gd z − (−dP), (3.41)

40 Norman Epstein

P+dP

ρU

Kinetic pressure from

gas crossflow. Radial

component of pressure

from weight of bed

SPOUT

ANNULUS

+dσ

+dU

Figure 3.2. Force balance model, after Mamuro and Hattori.

(From Epstein and Levine,

courtesy of Cambridge University Press.)

where σ

is the net downward solids force per cross-sectional area of the annulus.

Assuming, after Janssen (cited by Brown and Richards

), that σ

, the vertical component

of solids pressure, is proportional to the radial component, σ

, which in turn is in balance

with the kinetic pressure owing to crossﬂow velocity U

of ﬂuid from the spout into the

annulus, then

= κσ

= κρU

/2, (3.42)

where the constant κ is the r eciprocal of the Janssen proportionality ratio. Differentiating

with respect to z, we obtain

dσ

/dz = κρU

(dU

/dz). (3.43)

Substituting Eq. (3.43) into Eq. (3.41) results in

κρU

(dU

/dz) + (ρ

− ρ)

(

1 − ε

)

g =−dP/dz. (3.44)

If we assume invariance of annulus voidage with bed level (an assumption that, as we

shall see, is fully justiﬁed only at U ≈ U

), and neglect the annular solids motion (zero

at U ≈ U

) relative to that of the ﬂuid, we can write

−dP/dz = K

+ K

, (3.45)

in which, according to Ergun,

150μ

(

1 − ε

)

and K

175ρ

(

1 − ε

)

φε

(3.46)

Empirical and analytical hydrodynamics 41

Eq. (3.45), the quadratic Forchheimer equation (as cited by Scheidegger

), is adopted

here rather than the linear viscous ﬂow equation based on Darcy’s law,

−dp/dz = K

(3.47)

adopted by Mamuro and Hattori,

because particle Reynolds numbers in the annulus

at the midlevel of the bed are typically in the range (e.g., Re

= 100) at which both

viscous and inertial effects are signiﬁcant.

Combination of Eqs. (3.44) and (3.45) leads to

κρU

(

/dz

)

+ (ρ

− ρ)

(

1 − ε

)

g = K

+ K

. (3.48)

Differentiating this equation with respect to z,

κρd

(

· dU

/dz

)

/dz = K

/dz + K





/dz. (3.49)

Assuming that the spout diameter D

, and hence the annulus cross-sectional area A

,is

independent of z, a ﬂuid balance over height dz yields

· π D

dz = A

. (3.50)

Substituting U

from Eq. (3.50) into Eq. (3.49) and rearranging gives





= F

+ F





, (3.51)

where

κρ A

and F

κρ A

. (3.52)

Eq. (3.51), a third-order nonlinear differential equation, requires three boundar y condi-

tions; these are initially taken as

B.C.(i): at z = 0, U

= 0

B.C.(ii): at z = H

, U

= U

aHm

= U

and

B.C.(iii): at z = H

, −dP/dz = (ρ

− ρ)(1 − ε

)g = (ρ

− ρ)(1 − ε

)g.

The ﬁrst boundary condition states that there is no ﬂuid in the annulus at the bottom

of the bed, whereas the second and third signify that the top of the bed is at minimum

ﬂuidization for a bed of maximum spoutable depth. From Eq. (3.44), the third condition

yields U

/dz = 0, and hence from Eq. ( 3.50) either dU

/dz = 0ord

/dz

= 0

or both are zero at H = H

[both turn out to be zero for the Mamuro-Hattori solution,

Eq. (3.65), based on Darcy’s law]. Here, based on abundant experimental data,

11,27,31

we assume simply that dU

/dz = 0atz = H

, which replaces B.C. (iii), even when

experimental estimates of

(

−dP/dz

)

fall somewhat short of (ρ

− ρ)(1 − ε

)g.

Integrating Eq. (3.51) once, we obtain

(

/dz

)



/dz



= F

+ F

. (3.53)

42 Norman Epstein

Substituting B.C. (ii) and the above replacement for B.C. (iii) into Eq. (3.53),

0 = F

+ F

. (3.54)

Subtracting Eq. (3.54) from Eq. (3.53) gives

(

/dz

)



/dz



= F



−U



+ F



−U



. (3.55)

Now let dU

/dz = 1/X, whence d

/dz

=−(dX/dU

)/ X

, so that Eq. (3.55)

becomes

−dX/X

= F

−U

)dU

+ F

−U

)dU

, (3.56)

which integrates to

1/3X

= F

/2 − F

+ F

/3 − F

+ C

. (3.57)

Again substituting B.C. (ii) and replacement B.C. (iii) into the above equation,

0 = F

/2 − F

+ F

/3 − F

. (3.58)

Subtracting Eq. (3.58) from Eq. (3.57) gives

1/3X

= F

−U

)

/2 + F

− 3U

+ 2U

)/3. (3.59)

If the second term on the r ight-hand side of Eq. (3.59) is neglected relative to the ﬁrst –

that is, we assume Darcy’s law, and write 1/X again as dU

/dz, then

/(U

−U

)

2/3

= (3F

/2)

1/3

dz. (3.60)

Integrating leads to

3(U

−U

)

1/3

= (3F

/2)

1/3

z +C. (3.61)

Substituting B.C. (ii), we obtain

0 = (3F

/2)

1/3

+C. (3.62)

Subtracting Eq. (3.62) from Eq. (3.61) and cubing the result, we ﬁnd that

−U

= (F

/18)(z − H

)

. (3.63)

Application of B.C. (i) gives

0 − U

= (F

/18)(0 − H

)

. (3.64)

Empirical and analytical hydrodynamics 43

Dividing Eq. (3.63) by Eq. (3.64) and rearranging leads to

= 1 −



1 −



, (3.65)

which is the well-known Mamuro-Hattori

equation.

Now, instead, proceed with Eq. (3.59), rewritten more compactly as

(dy/dz)

= F

(y − 1)

(y + β), (3.66)

where y = U

, so that dy/dz = 1/U

X, and

β =

+ 2 =

+ 2. (3.67)

To evaluate β, the constants K

and K

at minimum spouting conditions may be estimated

from Eq. (3.46) assuming ε

= ε

, or determined experimentally by measuring the

axial pressure g radient as a function of superﬁcial ﬂuid velocity for ﬂow through a

random loose-packed bed of the given solids. The voidage of such a bed is equal to

, as well as to that of a slowly moving packed bed,

and hence equals ε

,atleastat

minimum spouting. U

in Eq. (3.67) may be calculated from Eq. (3.29) or determined

experimentally. With the Ergun values of K

and K

, β in Eq. (3.67) then reduces to

[128.6(1 − ε

)/φ Re

] + 2. Thus, when Darcy’s law (creeping or viscous ﬂow) holds,

→ 0 and β →∞, whereas when inviscid ﬂow prevails, Re

→∞and β → 2.

Now deﬁne a new variable,

Y =−



β + y

1 − y



1/3

. (3.68)

Eq. (3.66) is then equivalent to

dz =

1/3

3YdY

1 − Y

, (3.69)

which can be separated into two parts,

dz =

1/3



1 − Y

Y − 1

1 + Y + Y



dY, (3.70)

and integrated to give

z = C

−

1/3



1 − Y

(1 + Y + Y

)

√

3arctan



1 + 2Y

√



. (3.71)

Substituting B.C. (ii), according to which y = 1, Y =−∞at z = H

= C

−



O +

√



−



. (3.72)

Subtracting Eq. (3.72) from Eq. (3.71) gives

z − H

=−

1/3



1 − Y

(1 + Y + Y

)

1/2

√



arctan



1 + 2Y

√





. (3.73)

44 Norman Epstein

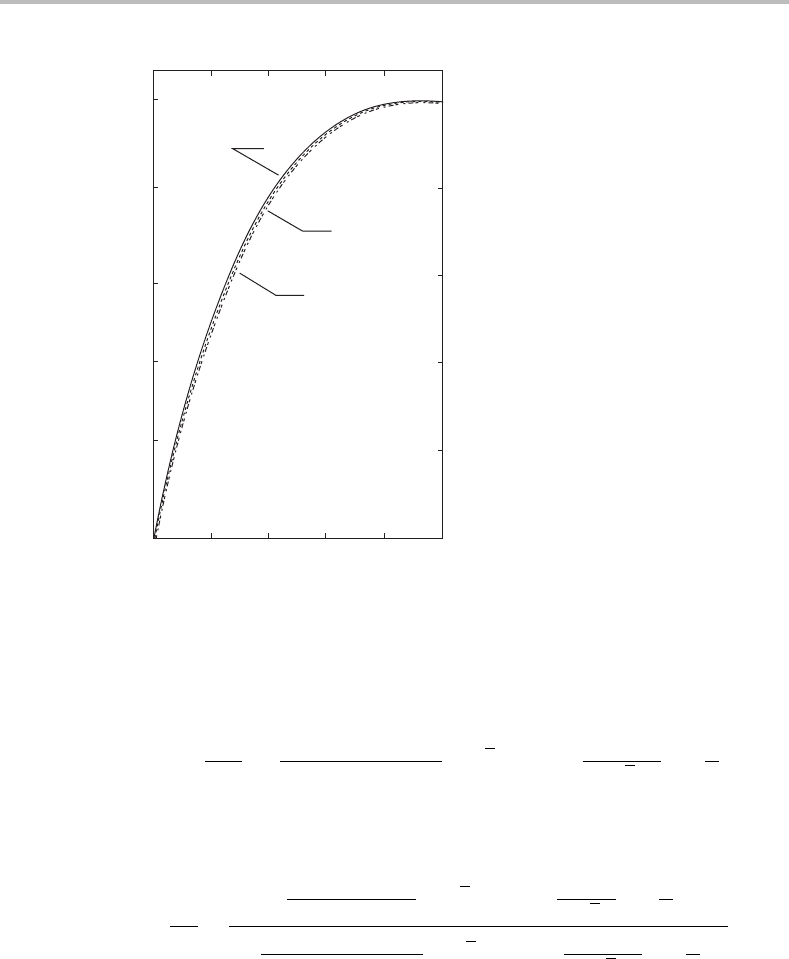
1.0

β =

∞

β = 5

β = 2

0.8

0.6

0.4

0.2

0 0.2 0.4 0.6 0.8 1.0

Z/H

Figure 3.3. The effect of the ﬂow regime parameter β on the normalized ﬂuid velocity proﬁle in

the spouted bed annulus as predicted by Eq. (3.75).

The curve for β =∞corresponds to

Eq. (3.65). (From Epstein et al.,

courtesy of Canadian Journal of Chemical Engineering.)

Substituting B.C. (i), according to which y = 0 and Y =−β

1/3

, we obtain

−H

=−

1/3



1 + β

1/3

(1 − β

1/3

+ β

2/3

)

1/2

√



arctan



1 − 2β

1/3

√





(3.74)

Dividing Eq. (3.73) by Eq. (3.74) leads to

1 −



1 − Y

(1 + Y + Y

)

1/2

√



arctan



1 + 2Y

√







1 + β

1/3

(1 − β

1/3

+ β

2/3

)

1/2

√



arctan



1 − 2β

1/3

√





(3.75)

which i s the Epstein-Levine

implicit solution for U

as a function of z/H

under

conditions in which both viscous and inertial forces are important.

If one expands the terms in both the numerator and denominator of Eq. (3.75) as

power series, and then allows β to approach inﬁnity, it can be shown

that this equation

collapses to Eq. (3.65) at the viscous ﬂow limit. The other extreme, inviscid ﬂow, is

represented by Eq. (3.75) with β = 2. Values of β for spouted beds are typically in

the range of 2.2 to 5. Figure 3.3 plots y = U

versus z/H

for the two extremes

Empirical and analytical hydrodynamics 45

and for an intermediate case, β = 5, which corresponds to Re

= 25 for spherical

particles. Surprisingly, the differences between the extremes is such that U

with

β =∞averages no more than 2 percent above U

with β = 2fromz/H

= 0to

z/H

= 1. These differences are certainly smaller than the experimental error involved

in measuring U

. Apparently it is the use of the same constraining boundary condition

= U

at z = H

, with respect to which both U

and z are normalized, that attenuates

the differences.

Eqs. (3.65) and (3.75) were both derived for H = H

, but to deal with beds for which

H < H

, Mamuro and Hattori

arbitrarily modiﬁed Eq. (3.65) to

= 1 −



1 −



. (3.76)

If B.C. (ii) above is simply changed to U

= U

at z = H and B.C. (iii) to σ

= 0at

z = H (i.e., zero vertical solids pressure at the top of the annulus), so from Eq. (3.42)

and (3.50), dU

/dz = 0atz = H, which now replaces B.C. (iii), then following the

same derivation sequence as for Eq. (3.65) results in Eq. (3.76). Empirically, however,

Eq. ( 3.76) fails

to give good prediction of U

as a function of z/H for H < H

Where this derivation of Eq. (3.76) errs is in the assumption that σ

= 0atz = H < H

The assumption σ

= 0 is reasonable at z = H = H

because spouting ceases when

H = H

, but not when H < H

, at which point spouting results in bombarding the

surface of the annulus with particles from the fountain.

There is a broad range of direct and indirect evidence

15,27,31,34

that, for a given column

geometry, spouting ﬂuid, and solids material, U

at any bed level, z, in the cylindrical

part of the column is independent of total bed depth, H, provided U ≈ U

. Hence

Eqs. (3.65) and (3.75) are both applicable to beds for which H ≤ H

and U ≈ U

Because of its greater simplicity, further discussion is focused on Eq. (3.65). This

equation was originally assumed to apply not only at U = U

, but also at U > U

However, longitudinal pressure gradients measured along the walls of spouting beds

indicated an apparent decline in U

at all bed levels as U was increased and hence an even

greater excess of gas ﬂow to the spout than the input excess over minimum spouting.

On the assumption that ε

= constant = ε

, this result was ﬁrst interpreted

as owing

to the increased circulation, and hence downﬂow of solids in the annulus, counteracting

the upward ﬂow of gas therein. However, subsequent measurements by He et al.

33,34

annulus voidages using optical ﬁber probes at U > U

have indicated, for a given solid

material, that for a ﬁxed value of H , ε

at any bed level increases with increasing U and

with increasing radial distance from the spout; that at any H and U/U

, ε

increases

with increasing z; and that at ﬁxed U /U

, U

at any bed level increases as H increases.

Thus the equality of pressure gradients often observed

27,31

at similar bed levels despite

large variations in H can no longer be interpreted as signifying equality of U

,giventhe

signiﬁcant differences in ε

at these levels. Similarly, any observed decline in pressure

gradients with U can now be better explained as originating from an increase in ε

rather than from a decrease in U

. Consequently, Eqs. (3.65) and (3.75), although they

remain applicable to H ≤ H

, must in all rigor be restricted to U = U

and should

therefore be interpreted as yielding minimum measurable values of U

– that is, values

46 Norman Epstein

that will be exceeded in most practical cases. The derivations of these equations also

neglect any variations of spout diameter with z, the small radial components of ﬂuid

velocity present in the cylindrical part of the column, and the more complex behavior

of both ﬂuid and solids in the conical-base region. They are therefore most in line with

experimental measurements in the cylindrical part of the column somewhat above the

cone (for U close to U

), particularly

24,34

if U

is replaced by the measured value of

aHm

The previous derivations take no account of the vertical shear stresses at the column

wall and at the spout–annulus interface. When these are taken into account, additional

variables such as the angle of wall friction and the angle of internal friction of the

particles are introduced into the problem.

The resulting equation for U

, based on

Darcy’s law, even when normalized with respect to U

aHm

measured at z = H

rather

than to U

, still contains one adjustable parameter,

estimation of which requires at

least one experimental measurement. Its added complexity thus gives it no advantage

over Eq. (3.65), rewritten for U ≥ U

aHm

αU

= 1 −



1 −



. (3.77)

Here α is an adjustable parameter with a value in the order of unity at U = U

. Uncer-

tainty with respect to U

aHm

can be sur mounted, after Grbav

c et al.,

by normalization

with respect to U

instead of U

aHm

– that is, by writing

1 − [1 − (z/H

)]

1 − [1 − (H/H

)]

. (3.78)

Eq. (3.78) is more reliably in agreement with experimental results than Eq. (3.65), but

unlike Eq. (3.65), use of Eq. (3.78) to predict U

(

)

requires that U

be measured.

3.4.2 Empirically based modeling

An alternative approach to annulus ﬂow i s based on the empirical ﬁnding of Lefroy and

Davidson

that at U ≈ U

, the longitudinal pressure distribution of a spouted bed can

be represented by

P − P

=−P

cos(π z/2H ), (3.79)

so for the particular case of H = H

P − P

(

−P

)

cos(π z/2H

). (3.80)

Differentiating Eq. (3.80) with respect to z, one obtains

−dP/dz = ( π/2H

)(−P

)

sin(π z/2H

), (3.81)

so at z = H

(

−dP/dz

)

(

π/2H

)(

−P

)

. (3.82)